| This article needs editing to comply with Misplaced Pages's Manual of Style. Please help improve the content. (November 2021) (Learn how and when to remove this message) |
| AVL tree | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | Tree | ||||||||||||||||||||||||||||
| Invented | 1962 | ||||||||||||||||||||||||||||
| Invented by | Georgy Adelson-Velsky and Evgenii Landis | ||||||||||||||||||||||||||||
| Complexities in big O notation | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||

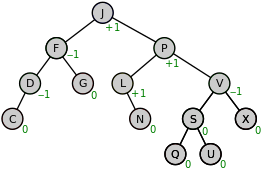
In computer science, an AVL tree (named after inventors Adelson-Velsky and Landis) is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.
The AVL tree is named after its two Soviet inventors, Georgy Adelson-Velsky and Evgenii Landis, who published it in their 1962 paper "An algorithm for the organization of information". It is the first self-balancing binary search tree data structure to be invented.
AVL trees are often compared with red–black trees because both support the same set of operations and take time for the basic operations. For lookup-intensive applications, AVL trees are faster than red–black trees because they are more strictly balanced. Similar to red–black trees, AVL trees are height-balanced. Both are, in general, neither weight-balanced nor -balanced for any ; that is, sibling nodes can have hugely differing numbers of descendants.
Definition
Balance factor
In a binary tree the balance factor of a node X is defined to be the height difference
of its two child sub-trees rooted by node X.
A node X with is called "left-heavy", one with is called "right-heavy", and one with is sometimes simply called "balanced".
Properties
Balance factors can be kept up-to-date by knowing the previous balance factors and the change in height – it is not necessary to know the absolute height. For holding the AVL balance information, two bits per node are sufficient.
The height (counted as the maximal number of levels) of an AVL tree with nodes lies in the interval:
where is the golden ratio and This is because an AVL tree of height contains at least nodes where is the Fibonacci sequence with the seed values
Operations
Read-only operations of an AVL tree involve carrying out the same actions as would be carried out on an unbalanced binary search tree, but modifications have to observe and restore the height balance of the sub-trees.
Searching
Searching for a specific key in an AVL tree can be done the same way as that of any balanced or unbalanced binary search tree. In order for search to work effectively it has to employ a comparison function which establishes a total order (or at least a total preorder) on the set of keys. The number of comparisons required for successful search is limited by the height h and for unsuccessful search is very close to h, so both are in O(log n).
Traversal
As a read-only operation the traversal of an AVL tree functions the same way as on any other binary tree. Exploring all n nodes of the tree visits each link exactly twice: one downward visit to enter the subtree rooted by that node, another visit upward to leave that node's subtree after having explored it.
Once a node has been found in an AVL tree, the next or previous node can be accessed in amortized constant time. Some instances of exploring these "nearby" nodes require traversing up to h ∝ log(n) links (particularly when navigating from the rightmost leaf of the root's left subtree to the root or from the root to the leftmost leaf of the root's right subtree; in the AVL tree of figure 1, navigating from node P to the next-to-the-right node Q takes 3 steps). Since there are n−1 links in any tree, the amortized cost is 2×(n−1)/n, or approximately 2.
Insert
When inserting a node into an AVL tree, you initially follow the same process as inserting into a Binary Search Tree. If the tree is empty, then the node is inserted as the root of the tree. If the tree is not empty, then we go down the root, and recursively go down the tree searching for the location to insert the new node. This traversal is guided by the comparison function. In this case, the node always replaces a NULL reference (left or right) of an external node in the tree i.e., the node is either made a left-child or a right-child of the external node.
After this insertion, if a tree becomes unbalanced, only ancestors of the newly inserted node are unbalanced. This is because only those nodes have their sub-trees altered. So it is necessary to check each of the node's ancestors for consistency with the invariants of AVL trees: this is called "retracing". This is achieved by considering the balance factor of each node.
Since with a single insertion the height of an AVL subtree cannot increase by more than one, the temporary balance factor of a node after an insertion will be in the range . For each node checked, if the temporary balance factor remains in the range from –1 to +1 then only an update of the balance factor and no rotation is necessary. However, if the temporary balance factor is ±2, the subtree rooted at this node is AVL unbalanced, and a rotation is needed. With insertion as the code below shows, the adequate rotation immediately perfectly rebalances the tree.
In figure 1, by inserting the new node Z as a child of node X the height of that subtree Z increases from 0 to 1.
- Invariant of the retracing loop for an insertion
The height of the subtree rooted by Z has increased by 1. It is already in AVL shape.
| Example code for an insert operation |
|---|
for (X = parent(Z); X != null; X = parent(Z)) { // Loop (possibly up to the root)
// BF(X) has to be updated:
if (Z == right_child(X)) { // The right subtree increases
if (BF(X) > 0) { // X is right-heavy
// ==> the temporary BF(X) == +2
// ==> rebalancing is required.
G = parent(X); // Save parent of X around rotations
if (BF(Z) < 0) // Right Left Case (see figure 3)
N = rotate_RightLeft(X, Z); // Double rotation: Right(Z) then Left(X)
else // Right Right Case (see figure 2)
N = rotate_Left(X, Z); // Single rotation Left(X)
// After rotation adapt parent link
} else {
if (BF(X) < 0) {
BF(X) = 0; // Z’s height increase is absorbed at X.
break; // Leave the loop
}
BF(X) = +1;
Z = X; // Height(Z) increases by 1
continue;
}
} else { // Z == left_child(X): the left subtree increases
if (BF(X) < 0) { // X is left-heavy
// ==> the temporary BF(X) == -2
// ==> rebalancing is required.
G = parent(X); // Save parent of X around rotations
if (BF(Z) > 0) // Left Right Case
N = rotate_LeftRight(X, Z); // Double rotation: Left(Z) then Right(X)
else // Left Left Case
N = rotate_Right(X, Z); // Single rotation Right(X)
// After rotation adapt parent link
} else {
if (BF(X) > 0) {
BF(X) = 0; // Z’s height increase is absorbed at X.
break; // Leave the loop
}
BF(X) = -1;
Z = X; // Height(Z) increases by 1
continue;
}
}
// After a rotation adapt parent link:
// N is the new root of the rotated subtree
// Height does not change: Height(N) == old Height(X)
parent(N) = G;
if (G != null) {
if (X == left_child(G))
left_child(G) = N;
else
right_child(G) = N;
} else
tree->root = N; // N is the new root of the total tree
break;
// There is no fall thru, only break; or continue;
}
// Unless loop is left via break, the height of the total tree increases by 1.
|
In order to update the balance factors of all nodes, first observe that all nodes requiring correction lie from child to parent along the path of the inserted leaf. If the above procedure is applied to nodes along this path, starting from the leaf, then every node in the tree will again have a balance factor of −1, 0, or 1.
The retracing can stop if the balance factor becomes 0 implying that the height of that subtree remains unchanged.
If the balance factor becomes ±1 then the height of the subtree increases by one and the retracing needs to continue.
If the balance factor temporarily becomes ±2, this has to be repaired by an appropriate rotation after which the subtree has the same height as before (and its root the balance factor 0).
The time required is O(log n) for lookup, plus a maximum of O(log n) retracing levels (O(1) on average) on the way back to the root, so the operation can be completed in O(log n) time.
Delete
The preliminary steps for deleting a node are described in section Binary search tree#Deletion. There, the effective deletion of the subject node or the replacement node decreases the height of the corresponding child tree either from 1 to 0 or from 2 to 1, if that node had a child.
Starting at this subtree, it is necessary to check each of the ancestors for consistency with the invariants of AVL trees. This is called "retracing".
Since with a single deletion the height of an AVL subtree cannot decrease by more than one, the temporary balance factor of a node will be in the range from −2 to +2. If the balance factor remains in the range from −1 to +1 it can be adjusted in accord with the AVL rules. If it becomes ±2 then the subtree is unbalanced and needs to be rotated. (Unlike insertion where a rotation always balances the tree, after delete, there may be BF(Z) ≠ 0 (see figures 2 and 3), so that after the appropriate single or double rotation the height of the rebalanced subtree decreases by one meaning that the tree has to be rebalanced again on the next higher level.) The various cases of rotations are described in section Rebalancing.
- Invariant of the retracing loop for a deletion
The height of the subtree rooted by N has decreased by 1. It is already in AVL shape.
| Example code for a delete operation |
|---|
for (X = parent(N); X != null; X = G) { // Loop (possibly up to the root)
G = parent(X); // Save parent of X around rotations
// BF(X) has not yet been updated!
if (N == left_child(X)) { // the left subtree decreases
if (BF(X) > 0) { // X is right-heavy
// ==> the temporary BF(X) == +2
// ==> rebalancing is required.
Z = right_child(X); // Sibling of N (higher by 2)
b = BF(Z);
if (b < 0) // Right Left Case (see figure 3)
N = rotate_RightLeft(X, Z); // Double rotation: Right(Z) then Left(X)
else // Right Right Case (see figure 2)
N = rotate_Left(X, Z); // Single rotation Left(X)
// After rotation adapt parent link
} else {
if (BF(X) == 0) {
BF(X) = +1; // N’s height decrease is absorbed at X.
break; // Leave the loop
}
N = X;
BF(N) = 0; // Height(N) decreases by 1
continue;
}
} else { // (N == right_child(X)): The right subtree decreases
if (BF(X) < 0) { // X is left-heavy
// ==> the temporary BF(X) == -2
// ==> rebalancing is required.
Z = left_child(X); // Sibling of N (higher by 2)
b = BF(Z);
if (b > 0) // Left Right Case
N = rotate_LeftRight(X, Z); // Double rotation: Left(Z) then Right(X)
else // Left Left Case
N = rotate_Right(X, Z); // Single rotation Right(X)
// After rotation adapt parent link
} else {
if (BF(X) == 0) {
BF(X) = -1; // N’s height decrease is absorbed at X.
break; // Leave the loop
}
N = X;
BF(N) = 0; // Height(N) decreases by 1
continue;
}
}
// After a rotation adapt parent link:
// N is the new root of the rotated subtree
parent(N) = G;
if (G != null) {
if (X == left_child(G))
left_child(G) = N;
else
right_child(G) = N;
} else
tree->root = N; // N is the new root of the total tree
if (b == 0)
break; // Height does not change: Leave the loop
// Height(N) decreases by 1 (== old Height(X)-1)
}
// If (b != 0) the height of the total tree decreases by 1.
|
The retracing can stop if the balance factor becomes ±1 (it must have been 0) meaning that the height of that subtree remains unchanged.
If the balance factor becomes 0 (it must have been ±1) then the height of the subtree decreases by one and the retracing needs to continue.
If the balance factor temporarily becomes ±2, this has to be repaired by an appropriate rotation. It depends on the balance factor of the sibling Z (the higher child tree in figure 2) whether the height of the subtree decreases by one –and the retracing needs to continue– or does not change (if Z has the balance factor 0) and the whole tree is in AVL-shape.
The time required is O(log n) for lookup, plus a maximum of O(log n) retracing levels (O(1) on average) on the way back to the root, so the operation can be completed in O(log n) time.
Set operations and bulk operations
In addition to the single-element insert, delete and lookup operations, several set operations have been defined on AVL trees: union, intersection and set difference. Then fast bulk operations on insertions or deletions can be implemented based on these set functions. These set operations rely on two helper operations, Split and Join. With the new operations, the implementation of AVL trees can be more efficient and highly-parallelizable.
The function Join on two AVL trees t1 and t2 and a key k will return a tree containing all elements in t1, t2 as well as k. It requires k to be greater than all keys in t1 and smaller than all keys in t2. If the two trees differ by height at most one, Join simply create a new node with left subtree t1, root k and right subtree t2. Otherwise, suppose that t1 is higher than t2 for more than one (the other case is symmetric). Join follows the right spine of t1 until a node c which is balanced with t2. At this point a new node with left child c, root k and right child t2 is created to replace c. The new node satisfies the AVL invariant, and its height is one greater than c. The increase in height can increase the height of its ancestors, possibly invalidating the AVL invariant of those nodes. This can be fixed either with a double rotation if invalid at the parent or a single left rotation if invalid higher in the tree, in both cases restoring the height for any further ancestor nodes. Join will therefore require at most two rotations. The cost of this function is the difference of the heights between the two input trees.
| Pseudocode implementation for the Join algorithm |
|---|
function JoinRightAVL(TL, k, TR)
(l, k', c) = expose(TL)
if (Height(c) <= Height(TR)+1)
T' = Node(c, k, TR)
if (Height(T') <= Height(l)+1) then return Node(l, k', T')
else return rotateLeft(Node(l, k', rotateRight(T')))
else
T' = JoinRightAVL(c, k, TR)
T'' = Node(l, k', T')
if (Height(T') <= Height(l)+1) return T''
else return rotateLeft(T'')
function JoinLeftAVL(TL, k, TR) /* symmetric to JoinRightAVL */ function Join(TL, k, TR)
if (Height(TL)>Height(TR)+1) return JoinRightAVL(TL, k, TR)
if (Height(TR)>Height(TL)+1) return JoinLeftAVL(TL, k, TR)
return Node(TL, k, TR)
Here Height(v) is the height of a subtree (node) v. (l,k,r) = expose(v) extracts v's left child l, the key k of v's root, and the right child r. Node(l,k,r) means to create a node of left child l, key k, and right child r. |
To split an AVL tree into two smaller trees, those smaller than key k, and those greater than key k, first draw a path from the root by inserting k into the AVL. After this insertion, all values less than k will be found on the left of the path, and all values greater than k will be found on the right. By applying Join, all the subtrees on the left side are merged bottom-up using keys on the path as intermediate nodes from bottom to top to form the left tree, and the right part is asymmetric. The cost of Split is O(log n), order of the height of the tree.
| Pseudocode implementation for the Split algorithm |
|---|
function Split(T, k)
if (T = nil) return (nil, false, nil)
(L,m,R) = expose(T)
if (k = m) return (L, true, R)
if (k<m)
(L',b,R') = Split(L,k)
return (L', b, Join(R', m, R))
if (k>m)
(L',b,R') = Split(R, k)
return (Join(L, m, L'), b, R'))
|
The union of two AVL trees t1 and t2 representing sets A and B, is an AVL t that represents A ∪ B.
| Pseudocode implementation for the Union algorithm |
|---|
function Union(t1, t2):
if t1 = nil:
return t2
if t2 = nil:
return t1
(t<, b, t>) = Split(t2, t1.root)
return Join(Union(left(t1), t<), t1.root, Union(right(t1), t>))
Here, Split is presumed to return two trees: one holding the keys less its input key, one holding the greater keys. (The algorithm is non-destructive, but an in-place destructive version exists as well.) |
The algorithm for intersection or difference is similar, but requires the Join2 helper routine that is the same as Join but without the middle key. Based on the new functions for union, intersection or difference, either one key or multiple keys can be inserted to or deleted from the AVL tree. Since Split calls Join but does not deal with the balancing criteria of AVL trees directly, such an implementation is usually called the "join-based" implementation.
The complexity of each of union, intersection and difference is for AVL trees of sizes and . More importantly, since the recursive calls to union, intersection or difference are independent of each other, they can be executed in parallel with a parallel depth . When , the join-based implementation has the same computational DAG as single-element insertion and deletion.
Rebalancing
If during a modifying operation the height difference between two child subtrees changes, this may, as long as it is < 2, be reflected by an adaption of the balance information at the parent. During insert and delete operations a (temporary) height difference of 2 may arise, which means that the parent subtree has to be "rebalanced". The given repair tools are the so-called tree rotations, because they move the keys only "vertically", so that the ("horizontal") in-order sequence of the keys is fully preserved (which is essential for a binary-search tree).
Let X be the node that has a (temporary) balance factor of −2 or +2. Its left or right subtree was modified. Let Z be the child with the higher subtree (see figures 2 and 3). Note that both children are in AVL shape by induction hypothesis.
In case of insertion this insertion has happened to one of Z's children in a way that Z's height has increased. In case of deletion this deletion has happened to the sibling t1 of Z in a way so that t1's height being already lower has decreased. (This is the only case where Z's balance factor may also be 0.)
There are four possible variants of the violation:
| Right Right | ⟹ Z is a right | child of its parent X and BF(Z) ≥ 0 | |
| Left Left | ⟹ Z is a left | child of its parent X and BF(Z) ≤ 0 | |
| Right Left | ⟹ Z is a right | child of its parent X and BF(Z) < 0 | |
| Left Right | ⟹ Z is a left | child of its parent X and BF(Z) > 0 |
And the rebalancing is performed differently:
| Right Right | ⟹ X is rebalanced with a | simple | rotation rotate_Left |
(see figure 2) | |
| Left Left | ⟹ X is rebalanced with a | simple | rotation rotate_Right |
(mirror-image of figure 2) | |
| Right Left | ⟹ X is rebalanced with a | double | rotation rotate_RightLeft |
(see figure 3) | |
| Left Right | ⟹ X is rebalanced with a | double | rotation rotate_LeftRight |
(mirror-image of figure 3) |
Thereby, the situations are denoted as C B, where C (= child direction) and B (= balance) come from the set { Left, Right } with Right := −Left. The balance violation of case C == B is repaired by a simple rotation rotate_(−C), whereas the case C != B is repaired by a double rotation rotate_CB.
The cost of a rotation, either simple or double, is constant.
Simple rotation
Figure 2 shows a Right Right situation. In its upper half, node X has two child trees with a balance factor of +2. Moreover, the inner child t23 of Z (i.e., left child when Z is right child, or right child when Z is left child) is not higher than its sibling t4. This can happen by a height increase of subtree t4 or by a height decrease of subtree t1. In the latter case, also the pale situation where t23 has the same height as t4 may occur.
The result of the left rotation is shown in the lower half of the figure. Three links (thick edges in figure 2) and two balance factors are to be updated.
As the figure shows, before an insertion, the leaf layer was at level h+1, temporarily at level h+2 and after the rotation again at level h+1. In case of a deletion, the leaf layer was at level h+2, where it is again, when t23 and t4 were of same height. Otherwise the leaf layer reaches level h+1, so that the height of the rotated tree decreases.

rotate_Left(X,Z)
- Code snippet of a simple left rotation
| Input: | X = root of subtree to be rotated left |
| Z = right child of X, Z is right-heavy | |
| with height == Height(LeftSubtree(X))+2 | |
| Result: | new root of rebalanced subtree |
node *rotate_Left(node *X, node *Z) {
// Z is by 2 higher than its sibling
t23 = left_child(Z); // Inner child of Z
right_child(X) = t23;
if (t23 != null)
parent(t23) = X;
left_child(Z) = X;
parent(X) = Z;
// 1st case, BF(Z) == 0,
// only happens with deletion, not insertion:
if (BF(Z) == 0) { // t23 has been of same height as t4
BF(X) = +1; // t23 now higher
BF(Z) = –1; // t4 now lower than X
} else
{ // 2nd case happens with insertion or deletion:
BF(X) = 0;
BF(Z) = 0;
}
return Z; // return new root of rotated subtree
}
Double rotation
Figure 3 shows a Right Left situation. In its upper third, node X has two child trees with a balance factor of +2. But unlike figure 2, the inner child Y of Z is higher than its sibling t4. This can happen by the insertion of Y itself or a height increase of one of its subtrees t2 or t3 (with the consequence that they are of different height) or by a height decrease of subtree t1. In the latter case, it may also occur that t2 and t3 are of the same height.
The result of the first, the right, rotation is shown in the middle third of the figure. (With respect to the balance factors, this rotation is not of the same kind as the other AVL single rotations, because the height difference between Y and t4 is only 1.) The result of the final left rotation is shown in the lower third of the figure. Five links (thick edges in figure 3) and three balance factors are to be updated.
As the figure shows, before an insertion, the leaf layer was at level h+1, temporarily at level h+2 and after the double rotation again at level h+1. In case of a deletion, the leaf layer was at level h+2 and after the double rotation it is at level h+1, so that the height of the rotated tree decreases.
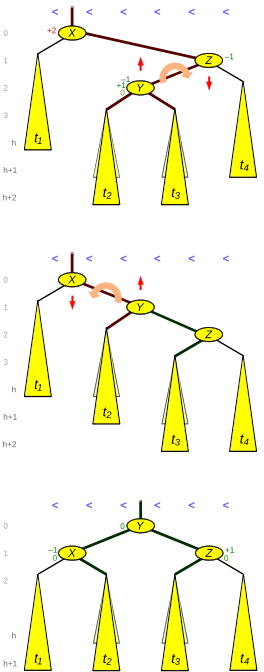
= rotate_Right around Z followed by
rotate_Left around X
- Code snippet of a right-left double rotation
| Input: | X = root of subtree to be rotated |
| Z = its right child, left-heavy | |
| with height == Height(LeftSubtree(X))+2 | |
| Result: | new root of rebalanced subtree |
node *rotate_RightLeft(node *X, node *Z) {
// Z is by 2 higher than its sibling
Y = left_child(Z); // Inner child of Z
// Y is by 1 higher than sibling
t3 = right_child(Y);
left_child(Z) = t3;
if (t3 != null)
parent(t3) = Z;
right_child(Y) = Z;
parent(Z) = Y;
t2 = left_child(Y);
right_child(X) = t2;
if (t2 != null)
parent(t2) = X;
left_child(Y) = X;
parent(X) = Y;
// 1st case, BF(Y) == 0
if (BF(Y) == 0) {
BF(X) = 0;
BF(Z) = 0;
} else if (BF(Y) > 0) {
// t3 was higher
BF(X) = –1; // t1 now higher
BF(Z) = 0;
} else {
// t2 was higher
BF(X) = 0;
BF(Z) = +1; // t4 now higher
}
BF(Y) = 0;
return Y; // return new root of rotated subtree
}
Comparison to other structures
Both AVL trees and red–black (RB) trees are self-balancing binary search trees and they are related mathematically. Indeed, every AVL tree can be colored red–black, but there are RB trees which are not AVL balanced. For maintaining the AVL (or RB) tree's invariants, rotations play an important role. In the worst case, even without rotations, AVL or RB insertions or deletions require O(log n) inspections and/or updates to AVL balance factors (or RB colors). RB insertions and deletions and AVL insertions require from zero to three tail-recursive rotations and run in amortized O(1) time, thus equally constant on average. AVL deletions requiring O(log n) rotations in the worst case are also O(1) on average. RB trees require storing one bit of information (the color) in each node, while AVL trees mostly use two bits for the balance factor, although, when stored at the children, one bit with meaning «lower than sibling» suffices. The bigger difference between the two data structures is their height limit.
For a tree of size n ≥ 1
- an AVL tree's height is at most
- where the golden ratio, and .
- a RB tree's height is at most
- .
AVL trees are more rigidly balanced than RB trees with an asymptotic relation AVL/RB ≈0.720 of the maximal heights. For insertions and deletions, Ben Pfaff shows in 79 measurements a relation of AVL/RB between 0.677 and 1.077 with median ≈0.947 and geometric mean ≈0.910.
See also
References
- ^ Eric Alexander. "AVL Trees". Archived from the original on July 31, 2019.
- Adelson-Velsky, Georgy; Landis, Evgenii (1962). "An algorithm for the organization of information". Proceedings of the USSR Academy of Sciences (in Russian). 146: 263–266. English translation by Myron J. Ricci in Soviet Mathematics - Doklady, 3:1259–1263, 1962.
- Sedgewick, Robert (1983). "Balanced Trees". Algorithms. Addison-Wesley. p. 199. ISBN 0-201-06672-6.
- ^ Pfaff, Ben (June 2004). "Performance Analysis of BSTs in System Software" (PDF). Stanford University.
- AVL trees are not weight-balanced? (meaning: AVL trees are not μ-balanced?)
Thereby: A Binary Tree is called -balanced, with , if for every node , the inequality - ^ Knuth, Donald E. (2000). Sorting and searching (2. ed., 6. printing, newly updated and rev. ed.). Boston : Addison-Wesley. ISBN 0-201-89685-0.
- However, the balance information can be kept in the child nodes as one bit indicating whether the parent is higher by 1 or by 2; thereby higher by 2 cannot occur for both children. This way the AVL tree is a "rank balanced" tree, as coined by Haeupler, Sen and Tarjan.
- Dixit, J. B. (2010). Mastering data structures through 'C' language. New Delhi, India: University Science Press, an imprint of Laxmi Publications Pvt. Ltd. ISBN 9789380386720. OCLC 939446542.
- ^ Brass, Peter (2008). Advanced data structures. Cambridge: Cambridge University Press. ISBN 9780511438202. OCLC 312435417.
- Hubbard, John Rast (2000). Schaum's outline of theory and problems of data structures with Java. New York: McGraw-Hill. ISBN 0071378707. OCLC 48139308.
- ^ Pfaff, Ben (2004). An Introduction to Binary Search Trees and Balanced Trees. Free Software Foundation, Inc.
- Weiss, Mark Allen (2006). Data structures and algorithm analysis in C++ (3rd ed.). Boston: Pearson Addison-Wesley. p. 145. ISBN 0-321-37531-9. OCLC 61278554.
- ^ Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2016), "Just join for parallel ordered sets", Symposium on Parallel Algorithms and Architectures, ACM, pp. 253–264, arXiv:1602.02120, doi:10.1145/2935764.2935768, ISBN 978-1-4503-4210-0, S2CID 2897793.
- Paul E. Black (2015-04-13). "AVL tree". Dictionary of Algorithms and Data Structures. National Institute of Standards and Technology. Retrieved 2016-07-02.
- Mehlhorn, Kurt; Sanders, Peter (2008). Algorithms and Data Structures. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/978-3-540-77978-0. ISBN 978-3-540-77977-3.
- Dinesh P. Mehta; Sartaj Sahni, eds. (2017-12-15). Handbook of Data Structures and Applications (2 ed.). New York: Chapman and Hall/CRC. doi:10.1201/9781315119335. ISBN 978-1-315-11933-5.
{{cite book}}:|journal=ignored (help) - Red–black tree#Proof of bounds
Further reading
- Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Pages 458–475 of section 6.2.3: Balanced Trees.
- Haeupler, Bernhard; Sen, Siddhartha; Tarjan, Robert E. (2015), "Rank-balanced trees" (PDF), ACM Transactions on Algorithms, 11 (4): Art. 30, 26, doi:10.1145/2689412, MR 3361215, S2CID 1407290.
External links
 This article incorporates public domain material from Paul E. Black. "AVL Tree". Dictionary of Algorithms and Data Structures. NIST.
This article incorporates public domain material from Paul E. Black. "AVL Tree". Dictionary of Algorithms and Data Structures. NIST.
| Tree data structures | |
|---|---|
| Search trees (dynamic sets/associative arrays) | |
| Heaps | |
| Tries | |
| Spatial data partitioning trees | |
| Other trees | |
| Data structures | |
|---|---|
| Types | |
| Abstract | |
| Arrays | |
| Linked | |
| Trees | |
| Graphs | |


 is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more
is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more  -balanced for any
-balanced for any  ; that is, sibling nodes can have hugely differing numbers of descendants.
; that is, sibling nodes can have hugely differing numbers of descendants.

 is called "left-heavy", one with
is called "left-heavy", one with  is called "right-heavy", and one with
is called "right-heavy", and one with  is sometimes simply called "balanced".
is sometimes simply called "balanced".
 (counted as the maximal number of levels) of an AVL tree with
(counted as the maximal number of levels) of an AVL tree with 
 is the
is the  This is because an AVL tree of height
This is because an AVL tree of height  nodes where
nodes where  is the
is the 
 for AVL trees of sizes
for AVL trees of sizes  and
and  . More importantly, since the recursive calls to union, intersection or difference are independent of each other, they can be executed
. More importantly, since the recursive calls to union, intersection or difference are independent of each other, they can be executed  . When
. When  , the join-based implementation has the same computational DAG as single-element insertion and deletion.
, the join-based implementation has the same computational DAG as single-element insertion and deletion.


 and
and  .
. .
. , if for every node
, if for every node  , the inequality
, the inequality

 is the number of nodes below the tree with
is the number of nodes below the tree with  is the left child node of
is the left child node of