| This article is missing information about Alfvén wave modes (e.g., inertial and kinetic modes) and the Alfvén Mach number. Please expand the article to include this information. Further details may exist on the talk page. (September 2022) |
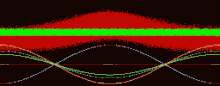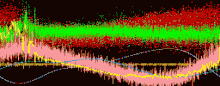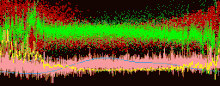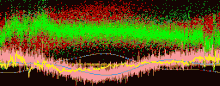
In plasma physics, an Alfvén wave, named after Hannes Alfvén, is a type of plasma wave in which ions oscillate in response to a restoring force provided by an effective tension on the magnetic field lines.
Definition
An Alfvén wave is a low-frequency (compared to the ion gyrofrequency) travelling oscillation of the ions and magnetic field in a plasma. The ion mass density provides the inertia and the magnetic field line tension provides the restoring force. Alfvén waves propagate in the direction of the magnetic field, and the motion of the ions and the perturbation of the magnetic field are transverse to the direction of propagation. However, Alfvén waves existing at oblique incidences will smoothly change into magnetosonic waves when the propagation is perpendicular to the magnetic field.
Alfvén waves are dispersionless.
Alfvén velocity
The low-frequency relative permittivity of a magnetized plasma is given by where B is the magnetic flux density, is the speed of light, is the permeability of the vacuum, and the mass density is the sum over all species of charged plasma particles (electrons as well as all types of ions). Here species has number density and mass per particle .
The phase velocity of an electromagnetic wave in such a medium is For the case of an Alfvén wave where is the Alfvén wave group velocity. (The formula for the phase velocity assumes that the plasma particles are moving at non-relativistic speeds, the mass-weighted particle velocity is zero in the frame of reference, and the wave is propagating parallel to the magnetic field vector.)
If , then . On the other hand, when , . That is, at high field or low density, the group velocity of the Alfvén wave approaches the speed of light, and the Alfvén wave becomes an ordinary electromagnetic wave.
Neglecting the contribution of the electrons to the mass density, , where is the ion number density and is the mean ion mass per particle, so that
Alfvén time
In plasma physics, the Alfvén time is an important timescale for wave phenomena. It is related to the Alfvén velocity by: where denotes the characteristic scale of the system. For example, could be the minor radius of the torus in a tokamak.
Relativistic case
The Alfvén wave velocity in relativistic magnetohydrodynamics is where e is the total energy density of plasma particles, is the total plasma pressure, and is the magnetic pressure. In the non-relativistic limit, where , this formula reduces to the one given previously.
History

The coronal heating problem
Further information: Stellar corona § Coronal heating problemThe study of Alfvén waves began from the coronal heating problem, a longstanding question in heliophysics. It was unclear why the temperature of the solar corona is hot (about one million kelvins) compared to its surface (the photosphere), which is only a few thousand kelvins. Intuitively, it would make sense to see a decrease in temperature when moving away from a heat source, but this does not seem to be the case even though the photosphere is denser and would generate more heat than the corona.
In 1942, Hannes Alfvén proposed in Nature the existence of an electromagnetic-hydrodynamic wave which would carry energy from the photosphere to heat up the corona and the solar wind. He claimed that the sun had all the necessary criteria to support these waves and they may in turn be responsible for sun spots. He stated:
If a conducting liquid is placed in a constant magnetic field, every motion of the liquid gives rise to an E.M.F. which produces electric currents. Owing to the magnetic field, these currents give mechanical forces which change the state of motion of the liquid. Thus a kind of combined electromagnetic–hydrodynamic wave is produced.
This would eventually turn out to be Alfvén waves. He received the 1970 Nobel Prize in Physics for this discovery.
Experimental studies and observations
The convection zone of the Sun, the region beneath the photosphere in which energy is transported primarily by convection, is sensitive to the motion of the core due to the rotation of the Sun. Together with varying pressure gradients beneath the surface, electromagnetic fluctuations produced in the convection zone induce random motion on the photospheric surface and produce Alfvén waves. The waves then leave the surface, travel through the chromosphere and transition zone, and interact with the ionized plasma. The wave itself carries energy and some of the electrically charged plasma.
In the early 1990s, de Pontieu and Haerendel suggested that Alfvén waves may also be associated with the plasma jets known as spicules. It was theorized these brief spurts of superheated gas were carried by the combined energy and momentum of their own upward velocity, as well as the oscillating transverse motion of the Alfvén waves.
In 2007, Alfvén waves were reportedly observed for the first time traveling towards the corona by Tomczyk et al., but their predictions could not conclude that the energy carried by the Alfvén waves was sufficient to heat the corona to its enormous temperatures, for the observed amplitudes of the waves were not high enough. However, in 2011, McIntosh et al. reported the observation of highly energetic Alfvén waves combined with energetic spicules which could sustain heating the corona to its million-kelvin temperature. These observed amplitudes (20.0 km/s against 2007's observed 0.5 km/s) contained over one hundred times more energy than the ones observed in 2007. The short period of the waves also allowed more energy transfer into the coronal atmosphere. The 50,000 km-long spicules may also play a part in accelerating the solar wind past the corona. Alfvén waves are routinely observed in solar wind, in particular in fast solar wind streams. The role of Alfvénic oscillations in the interaction between fast solar wind and the Earth's magnetosphere is currently under debate.
However, the above-mentioned discoveries of Alfvén waves in the complex Sun's atmosphere, starting from the Hinode era in 2007 for the next 10 years, mostly fall in the realm of Alfvénic waves essentially generated as a mixed mode due to transverse structuring of the magnetic and plasma properties in the localized flux tubes. In 2009, Jess et al. reported the periodic variation of H-alpha line-width as observed by Swedish Solar Telescope (SST) above chromospheric bright-points. They claimed first direct detection of the long-period (126–700 s), incompressible, torsional Alfvén waves in the lower solar atmosphere.
After the seminal work of Jess et al. (2009), in 2017 Srivastava et al. detected the existence of high-frequency torsional Alfvén waves in the Sun's chromospheric fine-structured flux tubes. They discovered that these high-frequency waves carry substantial energy capable of heating the Sun's corona and also originating the supersonic solar wind. In 2018, using spectral imaging observations, non-LTE (local thermodynamic equilibrium) inversions and magnetic field extrapolations of sunspot atmospheres, Grant et al. found evidence for elliptically polarized Alfvén waves forming fast-mode shocks in the outer regions of the chromospheric umbral atmosphere. They provided quantification of the degree of physical heat provided by the dissipation of such Alfvén wave modes above active region spots.
In 2024, a paper was published in the journal Science detailing a set of observations of what turned out to be the same jet of solar wind made by Parker Solar Probe and Solar Orbiter in February 2022, and implying Alfvén waves were what kept the jet's energy high enough to match the observations.
Historical timeline
- 1942: Alfvén suggests the existence of electromagnetic-hydromagnetic waves in a paper published in Nature 150, 405–406 (1942).
- 1949: Laboratory experiments by S. Lundquist produce such waves in magnetized mercury, with a velocity that approximated Alfvén's formula.
- 1949: Enrico Fermi uses Alfvén waves in his theory of cosmic rays.
- 1950: Alfvén publishes the first edition of his book, Cosmical Electrodynamics, detailing hydromagnetic waves, and discussing their application to both laboratory and space plasmas.
- 1952: Additional confirmation appears in experiments by Winston Bostick and Morton Levine with ionized helium.
- 1954: Bo Lehnert produces Alfvén waves in liquid sodium.
- 1958: Eugene Parker suggests hydromagnetic waves in the interstellar medium.
- 1958: Berthold, Harris, and Hope detect Alfvén waves in the ionosphere after the Argus nuclear test, generated by the explosion, and traveling at speeds predicted by Alfvén formula.
- 1958: Eugene Parker suggests hydromagnetic waves in the Solar corona extending into the Solar wind.
- 1959: D. F. Jephcott produces Alfvén waves in a gas discharge.
- 1959: C. H. Kelley and J. Yenser produce Alfvén waves in the ambient atmosphere.
- 1960: Coleman et al. report the measurement of Alfvén waves by the magnetometer aboard the Pioneer and Explorer satellites.
- 1961: Sugiura suggests evidence of hydromagnetic waves in the Earth's magnetic field.
- 1961: Normal Alfvén modes and resonances in liquid sodium are studied by Jameson.
- 1966: R. O. Motz generates and observes Alfvén waves in mercury.
- 1970: Hannes Alfvén wins the 1970 Nobel Prize in Physics for "fundamental work and discoveries in magneto-hydrodynamics with fruitful applications in different parts of plasma physics".
- 1973: Eugene Parker suggests hydromagnetic waves in the intergalactic medium.
- 1974: J. V. Hollweg suggests the existence of hydromagnetic waves in interplanetary space.
- 1977: Mendis and Ip suggest the existence of hydromagnetic waves in the coma of Comet Kohoutek.
- 1984: Roberts et al. predict the presence of standing MHD waves in the solar corona and opens the field of coronal seismology.
- 1999: Aschwanden et al. and Nakariakov et al. report the detection of damped transverse oscillations of solar coronal loops observed with the extreme ultraviolet (EUV) imager on board the Transition Region And Coronal Explorer (TRACE), interpreted as standing kink (or "Alfvénic") oscillations of the loops. This confirms the theoretical prediction of Roberts et al. (1984).
- 2007: Tomczyk et al. reported the detection of Alfvénic waves in images of the solar corona with the Coronal Multi-Channel Polarimeter (CoMP) instrument at the National Solar Observatory, New Mexico. However, these observations turned out to be kink waves of coronal plasma structures.doi:10.1051/0004-6361/200911840
- 2007: A special issue on the Hinode space observatory was released in the journal Science. Alfvén wave signatures in the coronal atmosphere were observed by Cirtain et al., Okamoto et al., and De Pontieu et al. By estimating the observed waves' energy density, De Pontieu et al. have shown that the energy associated with the waves is sufficient to heat the corona and accelerate the solar wind.
- 2008: Kaghashvili et al. uses driven wave fluctuations as a diagnostic tool to detect Alfvén waves in the solar corona.
- 2009: Jess et al. detect torsional Alfvén waves in the structured Sun's chromosphere using the Swedish Solar Telescope.
- 2011: Alfvén waves are shown to propagate in a liquid metal alloy made of Gallium.
- 2017: 3D numerical modelling performed by Srivastava et al. show that the high-frequency (12–42 mHz) Alfvén waves detected by the Swedish Solar Telescope can carry substantial energy to heat the Sun's inner corona.
- 2018: Using spectral imaging observations, non-LTE inversions and magnetic field extrapolations of sunspot atmospheres, Grant et al. found evidence for elliptically polarized Alfvén waves forming fast-mode shocks in the outer regions of the chromospheric umbral atmosphere. For the first time, these authors provided quantification of the degree of physical heat provided by the dissipation of such Alfvén wave modes.
- 2024: Alfvén waves are implied to be behind a smaller than expected energy loss in solar wind jets out as far as Venus' orbit, based on Parker Solar Probe and Solar Orbiter observations only two days apart.
See also
- Alfvén surface
- Computational magnetohydrodynamics
- Electrohydrodynamics
- Electromagnetic pump
- Ferrofluid
- Magnetic flow meter
- Magnetohydrodynamic turbulence
- MHD generator
- MHD sensor
- Molten salt
- Plasma stability
- Shocks and discontinuities (magnetohydrodynamics)
References
- Iwai, K; Shinya, K,; Takashi, K. and Moreau, R. (2003) "Pressure change accompanying Alfvén waves in a liquid metal" Magnetohydrodynamics 39(3): pp. 245-250, page 245
- Chen, F.F. (2016). Introduction to Plasma Physics and Controlled Fusion (3rd ed.). Switzerland: Springer International Publishing. pp. 55, 126–131.
- Gedalin, M. (1993). "Linear waves in relativistic anisotropic magnetohydrodynamics". Physical Review E. 47 (6): 4354–4357. Bibcode:1993PhRvE..47.4354G. doi:10.1103/PhysRevE.47.4354. PMID 9960513.
- Alfvén, Hannes (1942). "Existence of electromagnetic–hydrodynamic waves". Nature. 150 (3805): 405–406. Bibcode:1942Natur.150..405A. doi:10.1038/150405d0. S2CID 4072220.
- Bart de Pontieu (18 December 1997). "Chromospheric Spicules driven by Alfvén waves". Max-Planck-Institut für extraterrestrische Physik. Archived from the original on 16 July 2002. Retrieved 1 April 2012.
- Gerhard Haerendel (1992). "Weakly damped Alfven waves as drivers of solar chromospheric spicules". Nature. 360 (6401): 241–243. Bibcode:1992Natur.360..241H. doi:10.1038/360241a0. S2CID 44454309.
- Tomczyk, S.; McIntosh, S.W.; Keil, S.L.; Judge, P.G.; Schad, T.; Seeley, D.H.; Edmondson, J. (2007). "Alfven waves in the solar corona". Science. 317 (5842): 1192–1196. Bibcode:2007Sci...317.1192T. doi:10.1126/science.1143304. PMID 17761876. S2CID 45840582.
- McIntosh; et al. (2011). "Alfvenic waves with sufficient energy to power the quiet solar corona and fast solar wind". Nature. 475 (7357): 477–480. Bibcode:2011Natur.475..477M. doi:10.1038/nature10235. PMID 21796206. S2CID 4336248.
- Karen Fox (27 July 2011). "SDO spots extra energy in the Sun's corona". NASA. Retrieved 2 April 2012.
- Pokhotelov, D.; Rae, I.J.; Murphy, K.R.; Mann, I.R. (8 June 2015). "The influence of solar wind variability on magnetospheric ULF wave power". Annales Geophysicae. 33 (6): 697–701. doi:10.5194/angeo-33-697-2015.
- Borovsky, J.E. (5 January 2023). "Further investigation of the effect of upstream solar-wind fluctuations on solar-wind/magnetosphere coupling: Is the effect real?". Frontiers in Astronomy and Space Sciences. 9: 1–18. doi:10.3389/fspas.2022.975135.
- ^ Jess, David B.; Mathioudakis, Mihalis; Erdélyi, Robert; Crockett, Philip J.; Keenan, Francis P.; Christian, Damian J. (20 March 2009). "Alfvén Waves in the Lower Solar Atmosphere". Science. 323 (5921): 1582–1585. arXiv:0903.3546. Bibcode:2009Sci...323.1582J. doi:10.1126/science.1168680. hdl:10211.3/172550. ISSN 0036-8075. PMID 19299614. S2CID 14522616.
- ^ Srivastava, Abhishek Kumar; Shetye, Juie; Murawski, Krzysztof; Doyle, John Gerard; Stangalini, Marco; Scullion, Eamon; Ray, Tom; Wójcik, Dariusz Patryk; Dwivedi, Bhola N. (3 March 2017). "High-frequency torsional Alfvén waves as an energy source for coronal heating". Scientific Reports. 7 (1): 43147. Bibcode:2017NatSR...743147S. doi:10.1038/srep43147. ISSN 2045-2322. PMC 5335648. PMID 28256538.
- ^ Grant, Samuel D. T.; Jess, David B.; Zaqarashvili, Teimuraz V.; Beck, Christian; Socas-Navarro, Hector; Aschwanden, Markus J.; Keys, Peter H.; Christian, Damian J.; Houston, Scott J.; Hewitt, Rebecca L. (2018), "Alfvén Wave Dissipation in the Solar Chromosphere", Nature Physics, 14 (5): 480–483, arXiv:1810.07712, Bibcode:2018NatPh..14..480G, doi:10.1038/s41567-018-0058-3, S2CID 119089600
- ^ Rivera, Yeimy J.; Badman, Samuel T.; Stevens, Michael L.; Verniero, Jaye L.; Stawarz, Julia E.; Shi, Chen; Raines, Jim M.; Paulson, Kristoff W.; Owen, Christopher J.; Niembro, Tatiana; Louarn, Philippe; Livi, Stefano A.; Lepri, Susan T.; Kasper, Justin C.; Horbury, Timothy S.; Halekas, Jasper S.; Dewey, Ryan M.; De Marco, Rossana; Bale, Stuart D. (30 August 2024). "In situ observations of large-amplitude Alfvén waves heating and accelerating the solar wind". Science. 385 (6712): 962–966. arXiv:2409.00267. doi:10.1126/science.adk6953. ISSN 0036-8075.
- Lehnert, Bo (15 May 1954). "Magneto-Hydrodynamic Waves in Liquid Sodium". Physical Review. 94 (4): 815–824. Bibcode:1954PhRv...94..815L. doi:10.1103/PhysRev.94.815.
- JEPHCOTT, D. F. (13 June 1959). "Alfvén Waves in a Gas Discharge". Nature. 183 (4676): 1652–1654. Bibcode:1959Natur.183.1652J. doi:10.1038/1831652a0. ISSN 0028-0836. S2CID 11487078.
- Sonett, C. P.; Smith, E. J.; Judge, D. L.; Coleman, P. J. (15 February 1960). "Current Systems in the Vestigial Geomagnetic Field: Explorer VI". Physical Review Letters. 4 (4): 161–163. Bibcode:1960PhRvL...4..161S. doi:10.1103/PhysRevLett.4.161.
- Sugiura, Masahisa (December 1961). "Evidence of low-frequency hydromagnetic waves in the exosphere". Journal of Geophysical Research. 66 (12): 4087–4095. Bibcode:1961JGR....66.4087S. doi:10.1029/jz066i012p04087. ISSN 0148-0227.
- Motz, Robin O. (1966). "Alfvén Wave Generation in a Spherical System". Physics of Fluids. 9 (2): 411–412. Bibcode:1966PhFl....9..411M. doi:10.1063/1.1761687. ISSN 0031-9171.
- Hollweg, J. V. (1974). "Hydromagnetic Waves in Interplanetary Space". Publications of the Astronomical Society of the Pacific. 86 (513): 561. Bibcode:1974PASP...86..561H. doi:10.1086/129646. ISSN 1538-3873.
- Mendis, D. A.; Ip, W. -H. (March 1977). "The ionospheres and plasma tails of comets". Space Science Reviews. 20 (2): 145–190. Bibcode:1977SSRv...20..145M. doi:10.1007/bf02186863. ISSN 0038-6308. S2CID 119883598.
- Roberts, B.; Edwin, P. M.; Benz, A. O. (1984). "Coronal oscillations". The Astrophysical Journal. 279 (2): 857–865. Bibcode:1984ApJ...279..857R. doi:10.1086/161956. ISSN 0004-637X.
- Aschwanden, Markus J.; Fletcher, Lyndsay; Schrijver, Carolus J.; Alexander, David (1999). "Coronal Loop Oscillations Observed with the Transition Region and Coronal Explorer" (PDF). The Astrophysical Journal. 520 (2): 880. Bibcode:1999ApJ...520..880A. doi:10.1086/307502. ISSN 0004-637X. S2CID 122698505.
- Tomczyk, S.; McIntosh, S. W.; Keil, S. L.; Judge, P. G.; Schad, T.; Seeley, D. H.; Edmondson, J. (31 August 2007). "Alfvén Waves in the Solar Corona". Science. 317 (5842): 1192–1196. Bibcode:2007Sci...317.1192T. doi:10.1126/science.1143304. ISSN 0036-8075. PMID 17761876. S2CID 45840582.
- Doorsselaere, T. Van; Nakariakov, V. M.; Verwichte, E. (2008). "Detection of Waves in the Solar Corona: Kink or Alfvén?". The Astrophysical Journal Letters. 676 (1): L73. Bibcode:2008ApJ...676L..73V. doi:10.1086/587029. ISSN 1538-4357.
- "Science: 318 (5856)". Science. 318 (5856). 7 December 2007. ISSN 0036-8075.
- Cirtain, J. W.; Golub, L.; Lundquist, L.; Ballegooijen, A. van; Savcheva, A.; Shimojo, M.; DeLuca, E.; Tsuneta, S.; Sakao, T. (7 December 2007). "Evidence for Alfvén Waves in Solar X-ray Jets". Science. 318 (5856): 1580–1582. Bibcode:2007Sci...318.1580C. doi:10.1126/science.1147050. ISSN 0036-8075. PMID 18063786. S2CID 39318753.
- Okamoto, T. J.; Tsuneta, S.; Berger, T. E.; Ichimoto, K.; Katsukawa, Y.; Lites, B. W.; Nagata, S.; Shibata, K.; Shimizu, T. (7 December 2007). "Coronal Transverse Magnetohydrodynamic Waves in a Solar Prominence". Science. 318 (5856): 1577–1580. arXiv:0801.1958. Bibcode:2007Sci...318.1577O. doi:10.1126/science.1145447. ISSN 0036-8075. PMID 18063785. S2CID 121422620.
- Pontieu, B. De; McIntosh, S. W.; Carlsson, M.; Hansteen, V. H.; Tarbell, T. D.; Schrijver, C. J.; Title, A. M.; Shine, R. A.; Tsuneta, S. (7 December 2007). "Chromospheric Alfvénic Waves Strong Enough to Power the Solar Wind". Science. 318 (5856): 1574–1577. Bibcode:2007Sci...318.1574D. doi:10.1126/science.1151747. ISSN 0036-8075. PMID 18063784. S2CID 33655095.
- Kaghashvili, Edisher Kh.; Quinn, Richard A.; Hollweg, Joseph V. (2009). "Driven Waves as a Diagnostics Tool in the Solar Corona". The Astrophysical Journal. 703 (2): 1318. Bibcode:2009ApJ...703.1318K. doi:10.1088/0004-637x/703/2/1318. S2CID 120848530.
- Thierry Alboussière; Philippe Cardin; François Debray; Patrick La Rizza; Jean-Paul Masson; Franck Plunian; Adolfo Ribeiro; Denys Schmitt (2011). "Experimental evidence of Alfvén wave propagation in a Gallium alloy". Phys. Fluids. 23 (9): 096601. arXiv:1106.4727. Bibcode:2011PhFl...23i6601A. doi:10.1063/1.3633090. S2CID 2234120.
Further reading
| This "Further reading" section may need cleanup. Please read the editing guide and help improve the section. (July 2022) (Learn how and when to remove this message) |
- Alfvén, H. (1942), "Existence of electromagnetic-hydrodynamic waves", Nature, 150 (3805): 405–406, Bibcode:1942Natur.150..405A, doi:10.1038/150405d0, S2CID 4072220
- Alfvén, H. (1981), Cosmic Plasma, Holland: Reidel, ISBN 978-90-277-1151-9
- Aschwanden, M. J.; Fletcher, L.; Schrijver, C. J.; Alexander, D. (1999), "Coronal Loop Oscillations Observed with the Transition Region and Coronal Explorer" (PDF), The Astrophysical Journal, 520 (2): 880–894, Bibcode:1999ApJ...520..880A, doi:10.1086/307502, S2CID 122698505
- Berthold, W. K.; Harris, A. K.; Hope, H. J. (1960), "World-Wide Effects of Hydromagnetic Waves Due to Argus", Journal of Geophysical Research, 65 (8): 2233–2239, Bibcode:1960JGR....65.2233B, doi:10.1029/JZ065i008p02233
- Bostick, Winston H.; Levine, Morton A. (1952), "Experimental Demonstration in the Laboratory of the Existence of Magneto-Hydrodynamic Waves in Ionized Helium", Physical Review, 87 (4): 671, Bibcode:1952PhRv...87..671B, doi:10.1103/PhysRev.87.671
- Coleman, P. J. Jr.; Sonett, C. P.; Judge, D. L.; Smith, E. J. (1960), "Some Preliminary Results of the Pioneer V Magnetometer Experiment", Journal of Geophysical Research, 65 (6): 1856–1857, Bibcode:1960JGR....65.1856C, doi:10.1029/JZ065i006p01856
- Cramer, N. F.; Vladimirov, S. V. (1997), "Alfvén Waves in Dusty Interstellar Clouds", Publications of the Astronomical Society of Australia, 14 (2): 170–178, Bibcode:1997PASA...14..170C, doi:10.1071/AS97170
- Dessler, A. J. (1970), "Swedish iconoclast recognized after many years of rejection and obscurity", Science, 170 (3958): 604–606, Bibcode:1970Sci...170..604D, doi:10.1126/science.170.3958.604, PMID 17799293
- Falceta-Gonçalves, D.; Jatenco-Pereira, V. (2002), "The Effects of Alfvén Waves and Radiation Pressure in Dust Winds of Late-Type Stars", The Astrophysical Journal, 576 (2): 976–981, arXiv:astro-ph/0207342, Bibcode:2002ApJ...576..976F, doi:10.1086/341794, S2CID 429332
- Fermi, E. (1949), "On the Origin of the Cosmic Radiation", Physical Review, 75 (8): 1169–1174, Bibcode:1949PhRv...75.1169F, doi:10.1103/PhysRev.75.1169, S2CID 7070907
- Galtier, S. (2000), "A weak turbulence theory for incompressible magnetohydrodynamics", J. Plasma Physics, 63 (5): 447–488, arXiv:astro-ph/0008148, Bibcode:2000JPlPh..63..447G, doi:10.1017/S0022377899008284, S2CID 15528846
- Hollweg, J. V. (1974), "Hydromagnetic waves in interplanetary space", Publications of the Astronomical Society of the Pacific, 86 (October 1974): 561–594, Bibcode:1974PASP...86..561H, doi:10.1086/129646
- Ip, W.-H.; Mendis, D. A. (1975), "The cometary magnetic field and its associated electric currents", Icarus, 26 (4): 457–461, Bibcode:1975Icar...26..457I, doi:10.1016/0019-1035(75)90115-3
- Jephcott, D. F. (1959), "Alfvén waves in a gas discharge", Nature, 183 (4676): 1652–1654, Bibcode:1959Natur.183.1652J, doi:10.1038/1831652a0, S2CID 11487078
- Lehnert, Bo (1954), "Magneto-Hydrodynamic Waves in Liquid Sodium", Physical Review, 94 (4): 815–824, Bibcode:1954PhRv...94..815L, doi:10.1103/PhysRev.94.815
- Lundquist, S. (1949), "Experimental Investigations of Magneto-Hydrodynamic Waves", Physical Review, 76 (12): 1805–1809, Bibcode:1949PhRv...76.1805L, doi:10.1103/PhysRev.76.1805
- Mancuso, S.; Spangler, S. R. (1999), "Coronal Faraday Rotation Observations: Measurements and Limits on Plasma Inhomogeneities", The Astrophysical Journal, 525 (1): 195–208, Bibcode:1999ApJ...525..195M, doi:10.1086/307896, S2CID 122721188
- Motz, R. O. (1966), "Alfven Wave Generation in a Spherical System", Physics of Fluids, 9 (2): 411–412, Bibcode:1966PhFl....9..411M, doi:10.1063/1.1761687
- Nakariakov, V. M.; Ofman, L.; Deluca, E. E.; Roberts, B.; Davila, J. M. (1999), "TRACE observation of damped coronal loop oscillations: Implications for coronal heating", Science, 285 (5429): 862–864, Bibcode:1999Sci...285..862N, doi:10.1126/science.285.5429.862, PMID 10436148
- Ofman, L.; Wang, T. J. (2008), "Hinode observations of transverse waves with flows in coronal loops", Astronomy and Astrophysics, 482 (2): L9 – L12, Bibcode:2008A&A...482L...9O, doi:10.1051/0004-6361:20079340
- Otani, N. F. (1988a), "The Alfvén ion-cyclotron instability, simulation theory and techniques", Journal of Computational Physics, 78 (2): 251–277, Bibcode:1988JCoPh..78..251O, doi:10.1016/0021-9991(88)90049-6
- Otani, N. F. (1988b), "Application of Nonlinear Dynamical Invariants in a Single Electromagnetic Wave to the Study of the Alfvén-Ion-Cyclotron Instability", Physics of Fluids, 31 (6): 1456–1464, Bibcode:1988PhFl...31.1456O, doi:10.1063/1.866736
- Parker, E. N. (1955), "Hydromagnetic Waves and the Acceleration of Cosmic Rays", Physical Review, 99 (1): 241–253, Bibcode:1955PhRv...99..241P, doi:10.1103/PhysRev.99.241
- Parker, E. N. (1958), "Suprathermal Particle Generation in the Solar Corona", The Astrophysical Journal, 128: 677, Bibcode:1958ApJ...128..677P, doi:10.1086/146580
- Parker, E. N. (1973), "Extragalactic Cosmic Rays and the Galactic Magnetic Field", Astrophysics and Space Science, 24 (1): 279–288, Bibcode:1973Ap&SS..24..279P, doi:10.1007/BF00648691, S2CID 119623745
- Silberstein, M.; Otani, N. F. (1994), "Computer simulation of Alfvén waves and double layers along auroral magnetic field lines" (PDF), Journal of Geophysical Research, 99 (A4): 6351–6365, Bibcode:1994JGR....99.6351S, doi:10.1029/93JA02963
- Sugiura, Masahisa (1961), "Some Evidence of Hydromagnetic Waves in the Earth's Magnetic Field", Physical Review Letters, 6 (6): 255–257, Bibcode:1961PhRvL...6..255S, doi:10.1103/PhysRevLett.6.255
- Tomczyk, S.; McIntosh, S. W.; Keil, S. L.; Judge, P. G.; Schad, T.; Seeley, D. H.; Edmondson, J. (2007), "Waves in the Solar Corona", Science, 317 (5842): 1192–1196, Bibcode:2007Sci...317.1192T, doi:10.1126/science.1143304, PMID 17761876, S2CID 45840582
- Van Doorsselaere, T.; Nakariakov, V. M.; Verwichte, E. (2008), "Detection of Waves in the Solar Corona: Kink or Alfvén?", The Astrophysical Journal, 676 (1): L73 – L75, Bibcode:2008ApJ...676L..73V, CiteSeerX 10.1.1.460.1896, doi:10.1086/587029, S2CID 22933645
- Vasheghani Farahani, S.; Van Doorsselaere, T.; Verwichte, E.; Nakariakov, V. M. (2009), "Propagating transverse waves in soft X-ray coronal jets", Astronomy and Astrophysics, 498 (2): L29 – L32, Bibcode:2009A&A...498L..29V, doi:10.1051/0004-6361/200911840
- Jess, David B.; Mathioudakis, Mihalis; Erdélyi, Robert; Crockett, Philip J.; Keenan, Francis P.; Christian, Damian J. (2009), "Alfvén Waves in the Lower Solar Atmosphere", Science, 323 (5921): 1582–1585, arXiv:0903.3546, Bibcode:2009Sci...323.1582J, doi:10.1126/science.1168680, hdl:10211.3/172550, PMID 19299614, S2CID 14522616
- Srivastava, Abhishek K.; Shetye, Juie; Murawski, Krzysztof; Doyle, John Gerard; Stangalini, Marco; Scullion, Eamon; Ray, Tom; Wójcik, Dariusz Patryk; Dwivedi, Bhola N. (2017), "High-frequency torsional Alfvén waves as an energy source for coronal heating", Scientific Reports, 7: id.43147, Bibcode:2017NatSR...743147S, doi:10.1038/srep43147, PMC 5335648, PMID 28256538
- Grant, Samuel D. T.; Jess, David B.; Zaqarashvili, Teimuraz V.; Beck, Christian; Socas-Navarro, Hector; Aschwanden, Markus J.; Keys, Peter H.; Christian, Damian J.; Houston, Scott J.; Hewitt, Rebecca L. (2018), "Alfvén Wave Dissipation in the Solar Chromosphere", Nature Physics, 14 (5): 480–483, arXiv:1810.07712, Bibcode:2018NatPh..14..480G, doi:10.1038/s41567-018-0058-3, S2CID 119089600
- Murtaza, Ghulam. "Alfven wave propagation in dusty atoms" (PDF). NCP. Retrieved 9 May 2020.
External links
- Mysterious Solar Ripples Detected Dave Mosher 2 September 2007 Space.com
- EurekAlert! notification of 7 December 2007 Science special issue
- EurekAlert! notification: "Scientists find solution to solar puzzle"
 of a magnetized plasma is given by
of a magnetized plasma is given by
 where B is the
where B is the  is the
is the  is the
is the  over all species of charged plasma particles (electrons as well as all types of ions).
Here species
over all species of charged plasma particles (electrons as well as all types of ions).
Here species  has number density
has number density  and mass per particle
and mass per particle  .
.
 For the case of an Alfvén wave
For the case of an Alfvén wave
 where
where
 is the Alfvén wave group velocity.
(The formula for the phase velocity assumes that the plasma particles are moving at non-relativistic speeds, the mass-weighted particle velocity is zero in the frame of reference, and the wave is propagating parallel to the magnetic field vector.)
is the Alfvén wave group velocity.
(The formula for the phase velocity assumes that the plasma particles are moving at non-relativistic speeds, the mass-weighted particle velocity is zero in the frame of reference, and the wave is propagating parallel to the magnetic field vector.)
 , then
, then  . On the other hand, when
. On the other hand, when  ,
,  . That is, at high field or low density, the group velocity of the Alfvén wave approaches the speed of light, and the Alfvén wave becomes an ordinary electromagnetic wave.
. That is, at high field or low density, the group velocity of the Alfvén wave approaches the speed of light, and the Alfvén wave becomes an ordinary electromagnetic wave.
 , where
, where  is the ion number density and
is the ion number density and  is the mean ion mass per particle, so that
is the mean ion mass per particle, so that

 is an important timescale for wave phenomena. It is related to the Alfvén velocity by:
is an important timescale for wave phenomena. It is related to the Alfvén velocity by:
 where
where  denotes the characteristic scale of the system. For example,
denotes the characteristic scale of the system. For example,  where e is the total energy density of plasma particles,
where e is the total energy density of plasma particles,  is the total plasma pressure, and
is the total plasma pressure, and
 is the
is the  , this formula reduces to the one given previously.
, this formula reduces to the one given previously.