Chart used to show conditions at which physical phases of a substance occur For the use of this term in mathematics and physics, see Phase portrait and Phase space.

A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chart used to show conditions (pressure, temperature, etc.) at which thermodynamically distinct phases (such as solid, liquid or gaseous states) occur and coexist at equilibrium.
Overview
Common components of a phase diagram are lines of equilibrium or phase boundaries, which refer to lines that mark conditions under which multiple phases can coexist at equilibrium. Phase transitions occur along lines of equilibrium. Metastable phases are not shown in phase diagrams as, despite their common occurrence, they are not equilibrium phases.
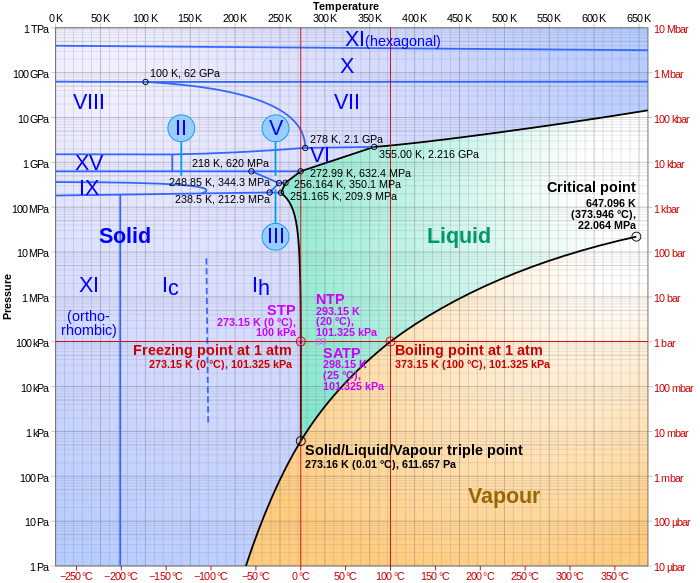
Triple points are points on phase diagrams where lines of equilibrium intersect. Triple points mark conditions at which three different phases can coexist. For example, the water phase diagram has a triple point corresponding to the single temperature and pressure at which solid, liquid, and gaseous water can coexist in a stable equilibrium (273.16 K and a partial vapor pressure of 611.657 Pa). The pressure on a pressure-temperature diagram (such as the water phase diagram shown) is the partial pressure of the substance in question.
The solidus is the temperature below which the substance is stable in the solid state. The liquidus is the temperature above which the substance is stable in a liquid state. There may be a gap between the solidus and liquidus; within the gap, the substance consists of a mixture of crystals and liquid (like a "slurry").
Working fluids are often categorized on the basis of the shape of their phase diagram.
Types
2-dimensional diagrams
Pressure vs temperature
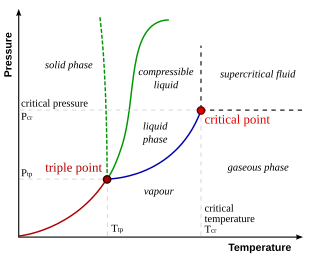
The simplest phase diagrams are pressure–temperature diagrams of a single simple substance, such as water. The axes correspond to the pressure and temperature. The phase diagram shows, in pressure–temperature space, the lines of equilibrium or phase boundaries between the three phases of solid, liquid, and gas.
The curves on the phase diagram show the points where the free energy (and other derived properties) becomes non-analytic: their derivatives with respect to the coordinates (temperature and pressure in this example) change discontinuously (abruptly). For example, the heat capacity of a container filled with ice will change abruptly as the container is heated past the melting point. The open spaces, where the free energy is analytic, correspond to single phase regions. Single phase regions are separated by lines of non-analytical behavior, where phase transitions occur, which are called phase boundaries.
In the diagram on the right, the phase boundary between liquid and gas does not continue indefinitely. Instead, it terminates at a point on the phase diagram called the critical point. This reflects the fact that, at extremely high temperatures and pressures, the liquid and gaseous phases become indistinguishable, in what is known as a supercritical fluid. In water, the critical point occurs at around Tc = 647.096 K (373.946 °C), pc = 22.064 MPa (217.75 atm) and ρc = 356 kg/m.
The existence of the liquid–gas critical point reveals a slight ambiguity in labelling the single phase regions. When going from the liquid to the gaseous phase, one usually crosses the phase boundary, but it is possible to choose a path that never crosses the boundary by going to the right of the critical point. Thus, the liquid and gaseous phases can blend continuously into each other. The solid–liquid phase boundary can only end in a critical point if the solid and liquid phases have the same symmetry group.
For most substances, the solid–liquid phase boundary (or fusion curve) in the phase diagram has a positive slope so that the melting point increases with pressure. This is true whenever the solid phase is denser than the liquid phase. The greater the pressure on a given substance, the closer together the molecules of the substance are brought to each other, which increases the effect of the substance's intermolecular forces. Thus, the substance requires a higher temperature for its molecules to have enough energy to break out of the fixed pattern of the solid phase and enter the liquid phase. A similar concept applies to liquid–gas phase changes.
Water is an exception which has a solid-liquid boundary with negative slope so that the melting point decreases with pressure. This occurs because ice (solid water) is less dense than liquid water, as shown by the fact that ice floats on water. At a molecular level, ice is less dense because it has a more extensive network of hydrogen bonding which requires a greater separation of water molecules. Other exceptions include antimony and bismuth.
At very high pressures above 50 GPa (500 000 atm), liquid nitrogen undergoes a liquid-liquid phase transition to a polymeric form and becomes denser than solid nitrogen at the same pressure. Under these conditions therefore, solid nitrogen also floats in its liquid.
The value of the slope dP/dT is given by the Clausius–Clapeyron equation for fusion (melting)
where ΔHfus is the heat of fusion which is always positive, and ΔVfus is the volume change for fusion. For most substances ΔVfus is positive so that the slope is positive. However for water and other exceptions, ΔVfus is negative so that the slope is negative.
Other thermodynamic properties
In addition to temperature and pressure, other thermodynamic properties may be graphed in phase diagrams. Examples of such thermodynamic properties include specific volume, specific enthalpy, or specific entropy. For example, single-component graphs of temperature vs. specific entropy (T vs. s) for water/steam or for a refrigerant are commonly used to illustrate thermodynamic cycles such as a Carnot cycle, Rankine cycle, or vapor-compression refrigeration cycle.
Any two thermodynamic quantities may be shown on the horizontal and vertical axes of a two-dimensional diagram. Additional thermodynamic quantities may each be illustrated in increments as a series of lines—curved, straight, or a combination of curved and straight. Each of these iso-lines represents the thermodynamic quantity at a certain constant value.
- Chart in U.S. units
-
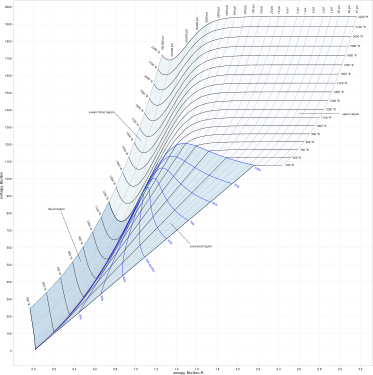 enthalpy–entropy (h–s) diagram for steam
enthalpy–entropy (h–s) diagram for steam
-
 pressure–enthalpy (p–h) diagram for steam
pressure–enthalpy (p–h) diagram for steam
-
 temperature–entropy (T–s) diagram for steam
temperature–entropy (T–s) diagram for steam
3-dimensional diagrams
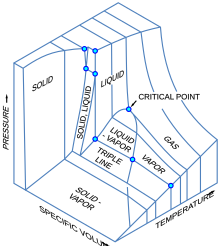
It is possible to envision three-dimensional (3D) graphs showing three thermodynamic quantities. For example, for a single component, a 3D Cartesian coordinate type graph can show temperature (T) on one axis, pressure (p) on a second axis, and specific volume (v) on a third. Such a 3D graph is sometimes called a p–v–T diagram. The equilibrium conditions are shown as curves on a curved surface in 3D with areas for solid, liquid, and vapor phases and areas where solid and liquid, solid and vapor, or liquid and vapor coexist in equilibrium. A line on the surface called a triple line is where solid, liquid and vapor can all coexist in equilibrium. The critical point remains a point on the surface even on a 3D phase diagram.
An orthographic projection of the 3D p–v–T graph showing pressure and temperature as the vertical and horizontal axes collapses the 3D plot into the standard 2D pressure–temperature diagram. When this is done, the solid–vapor, solid–liquid, and liquid–vapor surfaces collapse into three corresponding curved lines meeting at the triple point, which is the collapsed orthographic projection of the triple line.
Binary mixtures

Other much more complex types of phase diagrams can be constructed, particularly when more than one pure component is present. In that case, concentration becomes an important variable. Phase diagrams with more than two dimensions can be constructed that show the effect of more than two variables on the phase of a substance. Phase diagrams can use other variables in addition to or in place of temperature, pressure and composition, for example the strength of an applied electrical or magnetic field, and they can also involve substances that take on more than just three states of matter. One type of phase diagram plots temperature against the relative concentrations of two substances in a binary mixture called a binary phase diagram, as shown at right. Such a mixture can be either a solid solution, eutectic or peritectic, among others. These two types of mixtures result in very different graphs. Another type of binary phase diagram is a boiling-point diagram for a mixture of two components, i. e. chemical compounds. For two particular volatile components at a certain pressure such as atmospheric pressure, a boiling-point diagram shows what vapor (gas) compositions are in equilibrium with given liquid compositions depending on temperature. In a typical binary boiling-point diagram, temperature is plotted on a vertical axis and mixture composition on a horizontal axis.
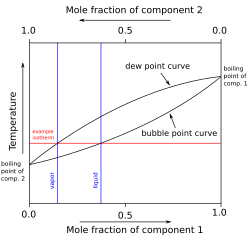
A two component diagram with components A and B in an "ideal" solution is shown. The construction of a liquid vapor phase diagram assumes an ideal liquid solution obeying Raoult's law and an ideal gas mixture obeying Dalton's law of partial pressure. A tie line from the liquid to the gas at constant pressure would indicate the two compositions of the liquid and gas respectively.
A simple example diagram with hypothetical components 1 and 2 in a non-azeotropic mixture is shown at right. The fact that there are two separate curved lines joining the boiling points of the pure components means that the vapor composition is usually not the same as the liquid composition the vapor is in equilibrium with. See Vapor–liquid equilibrium for more information.
In addition to the above-mentioned types of phase diagrams, there are many other possible combinations. Some of the major features of phase diagrams include congruent points, where a solid phase transforms directly into a liquid. There is also the peritectoid, a point where two solid phases combine into one solid phase during cooling. The inverse of this, when one solid phase transforms into two solid phases during cooling, is called the eutectoid.
A complex phase diagram of great technological importance is that of the iron–carbon system for less than 7% carbon (see steel).
The x-axis of such a diagram represents the concentration variable of the mixture. As the mixtures are typically far from dilute and their density as a function of temperature is usually unknown, the preferred concentration measure is mole fraction. A volume-based measure like molarity would be inadvisable.
Ternary phase diagrams
A system with three components is called a ternary system. At constant pressure the maximum number of independent variables is three – the temperature and two concentration values. For a representation of ternary equilibria a three-dimensional phase diagram is required. Often such a diagram is drawn with the composition as a horizontal plane and the temperature on an axis perpendicular to this plane. To represent composition in a ternary system an equilateral triangle is used, called Gibbs triangle (see also Ternary plot).
The temperature scale is plotted on the axis perpendicular to the composition triangle. Thus, the space model of a ternary phase diagram is a right-triangular prism. The prism sides represent corresponding binary systems A-B, B-C, A-C.
However, the most common methods to present phase equilibria in a ternary system are the following: 1) projections on the concentration triangle ABC of the liquidus, solidus, solvus surfaces; 2) isothermal sections; 3) vertical sections.
Crystals
Polymorphic and polyamorphic substances have multiple crystal or amorphous phases, which can be graphed in a similar fashion to solid, liquid, and gas phases.
Mesophases
Some organic materials pass through intermediate states between solid and liquid; these states are called mesophases. Attention has been directed to mesophases because they enable display devices and have become commercially important through the so-called liquid-crystal technology. Phase diagrams are used to describe the occurrence of mesophases.
See also
- CALPHAD (method)
- Computational thermodynamics
- Congruent melting and incongruent melting
- Gibbs phase rule
- Glass databases
- Hamiltonian mechanics
- Phase separation
- Saturation dome
- Schreinemaker's analysis
- Simple phase envelope algorithm
References
- "Phase Diagrams". ch302.cm.utexas.edu. Retrieved 14 July 2023.
- Predel, Bruno; Hoch, Michael J. R.; Pool, Monte (2004). Phase Diagrams and Heterogeneous Equilibria: A Practical Introduction. Springer. ISBN 978-3-540-14011-5.
- Papon, P.; Leblond, J.; Meijer, P. H. E. (2002). The Physics of Phase Transition : Concepts and Applications. Berlin: Springer. ISBN 978-3-540-43236-4.
- The International Association for the Properties of Water and Steam "Guideline on the Use of Fundamental Physical Constants and Basic Constants of Water", 2001, p. 5
- Landau, Lev D.; Lifshitz, Evgeny M. (1980). Statistical Physics. Vol. 5 (3rd ed.). Butterworth-Heinemann. ISBN 978-0-7506-3372-7.
- ^ Whitten, Kenneth W.; Galley, Kenneth D.; Davis, Raymond E. (1992). General Chemistry (4th ed.). Saunders College Publishing. p. 477. ISBN 9780030751561.
- Dorin, Henry; Demmin, Peter E.; Gabel, Dorothy L. (1992). Chemistry : The Study of Matter Prentice (Fourth ed.). Prentice Hall. pp. 266–273. ISBN 978-0-13-127333-7.
- Averill, Bruce A.; Eldredge, Patricia (2012). "11.7 Phase Diagrams". Principles of General Chemistry. Creative Commons.
- Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General Chemistry. Principles and Modern Applications (8th ed.). Prentice Hall. p. 495. ISBN 0-13-014329-4.
- Mukherjee, Goutam Dev; Boehler, Reinhard (30 November 2007). "High-Pressure Melting Curve of Nitrogen and the Liquid-Liquid Phase Transition". Physical Review Letters. 99 (22): 225701. Bibcode:2007PhRvL..99v5701M. doi:10.1103/PhysRevLett.99.225701. PMID 18233298.
- Laidler, Keith J.; Meiser, John H. (1982). Physical Chemistry. Benjamin/Cummings. pp. 173–74.
- Zemansky, Mark W.; Dittman, Richard H. (1981). Heat and Thermodynamics (6th ed.). McGraw-Hill. Figs. 2-3, 2-4, 2-5, 10-10, P10-1. ISBN 978-0-07-072808-0.
- Web applet: 3D Phase Diagrams for Water, Carbon Dioxide and Ammonia. Described in Glasser, Leslie; Herráez, Angel; Hanson, Robert M. (2009). "Interactive 3D Phase Diagrams Using Jmol". Journal of Chemical Education. 86 (5): 566. Bibcode:2009JChEd..86..566G. doi:10.1021/ed086p566. hdl:20.500.11937/11329.
- David, Carl W. (2022). "The phase diagram of a non-ideal mixture's p − v − x 2-component gas=liquid representation, including azeotropes". Chemistry Education Materials. University of Connecticut. Retrieved 9 April 2022.
- Alan Prince, "Alloy Phase Equilibria", Elsevier, 290 pp (1966) ISBN 978-0444404626
- A similar diagram may be found on the site Water structure and science. Water structure and science Site by Martin Chaplin, accessed 2 July 2015.
- Chandrasekhar, Sivaramakrishna (1992). Liquid Crystals (2nd ed.). Cambridge University Press. pp. 27–29, 356. ISBN 978-0-521-41747-1.
External links
- Iron-Iron Carbide Phase Diagram Example
- How to build a phase diagram
- Phase Changes: Phase Diagrams: Part 1 Archived 16 May 2009 at the Wayback Machine
- Equilibrium Fe-C phase diagram
- Phase diagrams for lead free solders Archived 27 July 2009 at the Wayback Machine
- DoITPoMS Phase Diagram Library
- DoITPoMS Teaching and Learning Package – "Phase Diagrams and Solidification"
- Phase Diagrams: The Beginning of Wisdom – Open Access Journal Article
- Binodal curves, tie-lines, lever rule and invariant points – How to read phase diagrams (Video by SciFox on TIB AV-Portal)
- The Alloy Phase Diagram International Commission (APDIC)
- Periodic table of phase diagrams of the elements (pdf poster)
| Chemical equilibria | |
|---|---|
| Concepts | |
| Models | |
| Applications | |
| Specific equilibria | |
| Chemical solutions | |
|---|---|
| Solution | |
| Concentration and related quantities | |
| Solubility | |
| Solvent | |


