| 5-cube 5-orthoplex compound | |
|---|---|
| Type | Compound |
| Schläfli symbol | {4,3,3,3} ∪ {3,3,3,4} |
| Coxeter diagram | |
| Intersection | Birectified 5-cube |
| Convex hull | dual of rectified 5-orthoplex |
| 5-polytopes | 2: 1 5-cube 1 5-orthoplex |
| Polychora | 42: 10 tesseract 32 16-cell |
| Polyhedra | 120: 40 cubes 80 tetrahedra |
| Faces | 160: 80 squares 80 triangles |
| Edges | 120 (80+40) |
| Vertices | 42 (32+10) |
| Symmetry group | B5, , order 3840 |
In 5-dimensional geometry, the 5-cube 5-orthoplex compound is a polytope compound composed of a regular 5-cube and dual regular 5-orthoplex. A compound polytope is a figure that is composed of several polytopes sharing a common center. The outer vertices of a compound can be connected to form a convex polytope called the convex hull. The compound is a facetting of the convex hull.
In 5-polytope compounds constructed as dual pairs, the hypercells and vertices swap positions and cells and edges swap positions. Because of this the number of hypercells and vertices are equal, as are cells and edges. Mid-edges of the 5-cube cross mid-cell in the 16-cell, and vice versa.
It can be seen as the 5-dimensional analogue of a compound of cube and octahedron.
Construction
The 42 Cartesian coordinates of the vertices of the compound are.
- 10: (±2, 0, 0, 0, 0), (0, ±2, 0, 0, 0), (0, 0, ±2, 0, 0), (0, 0, 0, ±2, 0), (0, 0, 0, 0, ±2)
- 32: (±1, ±1, ±1, ±1, ±1)
The convex hull of the vertices makes the dual of rectified 5-orthoplex.
The intersection of the 5-cube and 5-orthoplex compound is the uniform birectified 5-cube: ![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() ∩
∩ ![]()
![]()
![]()
![]()
![]() .
.
Images
The compound can be seen in projection as the union of the two polytope graphs. The convex hull as the dual of the rectified 5-orthoplex will have the same vertices, but different edges.
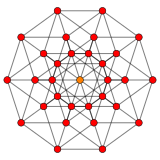 5-cube |
 5-orthoplex |
 Compound |
 Birectified 5-orthoplex (Intersection) |
References
- Klitzing, Richard. "Compound polytopes".
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
External links
- Olshevsky, George. "Cross polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Klitzing, Richard. "5D uniform polytopes (polytera) x3o3o3o4o - tac, o3o3o3o4x - pent".