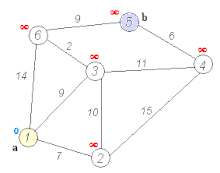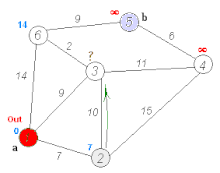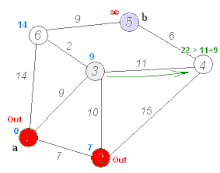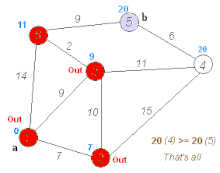
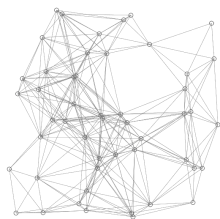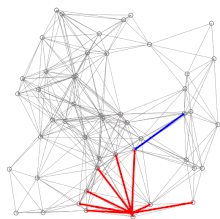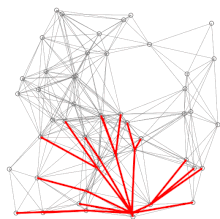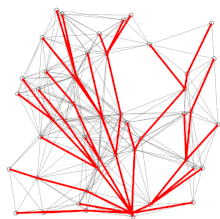
 Dijkstra's algorithm to find the shortest path between a and b. It picks the unvisited vertex with the lowest distance, calculates the distance through it to each unvisited neighbor, and updates the neighbor's distance if smaller. Mark visited (set to red) when done with neighbors. Dijkstra's algorithm to find the shortest path between a and b. It picks the unvisited vertex with the lowest distance, calculates the distance through it to each unvisited neighbor, and updates the neighbor's distance if smaller. Mark visited (set to red) when done with neighbors. | |
| Class | Search algorithm Greedy algorithm Dynamic programming |
|---|---|
| Data structure | Graph Usually used with priority queue or heap for optimization |
| Worst-case performance | |
Dijkstra's algorithm (/ˈdaɪkstrəz/ DYKE-strəz) is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, a road network. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.
Dijkstra's algorithm finds the shortest path from a given source node to every other node. It can be used to find the shortest path to a specific destination node, by terminating the algorithm after determining the shortest path to the destination node. For example, if the nodes of the graph represent cities, and the costs of edges represent the average distances between pairs of cities connected by a direct road, then Dijkstra's algorithm can be used to find the shortest route between one city and all other cities. A common application of shortest path algorithms is network routing protocols, most notably IS-IS (Intermediate System to Intermediate System) and OSPF (Open Shortest Path First). It is also employed as a subroutine in algorithms such as Johnson's algorithm.
The algorithm uses a min-priority queue data structure for selecting the shortest paths known so far. Before more advanced priority queue structures were discovered, Dijkstra's original algorithm ran in time, where is the number of nodes. Fredman & Tarjan 1984 proposed a Fibonacci heap priority queue to optimize the running time complexity to . This is asymptotically the fastest known single-source shortest-path algorithm for arbitrary directed graphs with unbounded non-negative weights. However, specialized cases (such as bounded/integer weights, directed acyclic graphs etc.) can be improved further. If preprocessing is allowed, algorithms such as contraction hierarchies can be up to seven orders of magnitude faster.
Dijkstra's algorithm is commonly used on graphs where the edge weights are positive integers or real numbers. It can be generalized to any graph where the edge weights are partially ordered, provided the subsequent labels (a subsequent label is produced when traversing an edge) are monotonically non-decreasing.
In many fields, particularly artificial intelligence, Dijkstra's algorithm or a variant offers a uniform cost search and is formulated as an instance of the more general idea of best-first search.
History
What is the shortest way to travel from Rotterdam to Groningen, in general: from given city to given city. It is the algorithm for the shortest path, which I designed in about twenty minutes. One morning I was shopping in Amsterdam with my young fiancée, and tired, we sat down on the café terrace to drink a cup of coffee and I was just thinking about whether I could do this, and I then designed the algorithm for the shortest path. As I said, it was a twenty-minute invention. In fact, it was published in '59, three years later. The publication is still readable, it is, in fact, quite nice. One of the reasons that it is so nice was that I designed it without pencil and paper. I learned later that one of the advantages of designing without pencil and paper is that you are almost forced to avoid all avoidable complexities. Eventually, that algorithm became to my great amazement, one of the cornerstones of my fame.
— Edsger Dijkstra, in an interview with Philip L. Frana, Communications of the ACM, 2001
Dijkstra thought about the shortest path problem while working as a programmer at the Mathematical Center in Amsterdam in 1956. He wanted to demonstrate the capabilities of the new ARMAC computer. His objective was to choose a problem and a computer solution that non-computing people could understand. He designed the shortest path algorithm and later implemented it for ARMAC for a slightly simplified transportation map of 64 cities in the Netherlands (he limited it to 64, so that 6 bits would be sufficient to encode the city number). A year later, he came across another problem advanced by hardware engineers working on the institute's next computer: minimize the amount of wire needed to connect the pins on the machine's back panel. As a solution, he re-discovered Prim's minimal spanning tree algorithm (known earlier to Jarník, and also rediscovered by Prim). Dijkstra published the algorithm in 1959, two years after Prim and 29 years after Jarník.
Algorithm

The algorithm requires a starting node, and node N, with a distance between the starting node and N. Dijkstra's algorithm starts with infinite distances and tries to improve them step by step:
- Create a set of all unvisited nodes: the unvisited set.
- Assign to every node a distance from start value: for the starting node, it is zero, and for all other nodes, it is infinity, since initially no path is known to these nodes. During execution, the distance of a node N is the length of the shortest path discovered so far between the starting node and N.
- From the unvisited set, select the current node to be the one with the smallest (finite) distance; initially, this is the starting node (distance zero). If the unvisited set is empty, or contains only nodes with infinite distance (which are unreachable), then the algorithm terminates by skipping to step 6. If the only concern is the path to a target node, the algorithm terminates once the current node is the target node. Otherwise, the algorithm continues.
- For the current node, consider all of its unvisited neighbors and update their distances through the current node; compare the newly calculated distance to the one currently assigned to the neighbor and assign the smaller one to it. For example, if the current node A is marked with a distance of 6, and the edge connecting it with its neighbor B has length 2, then the distance to B through A is 6 + 2 = 8. If B was previously marked with a distance greater than 8, then update it to 8 (the path to B through A is shorter). Otherwise, keep its current distance (the path to B through A is not the shortest).
- After considering all of the current node's unvisited neighbors, the current node is removed from the unvisited set. Thus a visited node is never rechecked, which is correct because the distance recorded on the current node is minimal (as ensured in step 3), and thus final. Repeat from to step 3.
- Once the loop exits (steps 3–5), every visited node contains its shortest distance from the starting node.
Description
Note: For ease of understanding, this discussion uses the terms intersection, road and map – however, in formal terminology these terms are vertex, edge and graph, respectively.The shortest path between two intersections on a city map can be found by this algorithm using pencil and paper. Every intersection is listed on a separate line: one is the starting point and is labeled (given a distance of) 0. Every other intersection is initially labeled with a distance of infinity. This is done to note that no path to these intersections has yet been established. At each iteration one intersection becomes the current intersection. For the first iteration, this is the starting point.
From the current intersection, the distance to every neighbor (directly-connected) intersection is assessed by summing the label (value) of the current intersection and the distance to the neighbor and then relabeling the neighbor with the lesser of that sum and the neighbor's existing label. I.e., the neighbor is relabeled if the path to it through the current intersection is shorter than previously assessed paths. If so, mark the road to the neighbor with an arrow pointing to it, and erase any other arrow that points to it. After the distances to each of the current intersection's neighbors have been assessed, the current intersection is marked as visited. The unvisited intersection with the smallest label becomes the current intersection and the process repeats until all nodes with labels less than the destination's label have been visited.
Once no unvisited nodes remain with a label smaller than the destination's label, the remaining arrows show the shortest path.
Pseudocode
In the following pseudocode, dist is an array that contains the current distances from the source to other vertices, i.e. dist is the current distance from the source to the vertex u. The prev array contains pointers to previous-hop nodes on the shortest path from source to the given vertex (equivalently, it is the next-hop on the path from the given vertex to the source). The code u ← vertex in Q with min dist, searches for the vertex u in the vertex set Q that has the least dist value. Graph.Edges(u, v) returns the length of the edge joining (i.e. the distance between) the two neighbor-nodes u and v. The variable alt on line 14 is the length of the path from the source node to the neighbor node v if it were to go through u. If this path is shorter than the current shortest path recorded for v, then the distance of v is updated to alt.
1 function Dijkstra(Graph, source): 2 3 for each vertex v in Graph.Vertices: 4 dist ← INFINITY 5 prev ← UNDEFINED 6 add v to Q 7 dist ← 0 8 9 while Q is not empty: 10 u ← vertex in Q with minimum dist 11 remove u from Q 12 13 for each neighbor v of u still in Q: 14 alt ← dist + Graph.Edges(u, v) 15 if alt < dist: 16 dist ← alt 17 prev ← u 18 19 return dist, prev
To find the shortest path between vertices source and target, the search terminates after line 10 if u = target. The shortest path from source to target can be obtained by reverse iteration:
1 S ← empty sequence 2 u ← target 3 if prev is defined or u = source: // Proceed if the vertex is reachable 4 while u is defined: // Construct the shortest path with a stack S 5 insert u at the beginning of S // Push the vertex onto the stack 6 u ← prev // Traverse from target to source
Now sequence S is the list of vertices constituting one of the shortest paths from source to target, or the empty sequence if no path exists.
A more general problem is to find all the shortest paths between source and target (there might be several of the same length). Then instead of storing only a single node in each entry of prev all nodes satisfying the relaxation condition can be stored. For example, if both r and source connect to target and they lie on different shortest paths through target (because the edge cost is the same in both cases), then both r and source are added to prev. When the algorithm completes, prev data structure describes a graph that is a subset of the original graph with some edges removed. Its key property is that if the algorithm was run with some starting node, then every path from that node to any other node in the new graph is the shortest path between those nodes graph, and all paths of that length from the original graph are present in the new graph. Then to actually find all these shortest paths between two given nodes, a path finding algorithm on the new graph, such as depth-first search would work.
Using a priority queue
A min-priority queue is an abstract data type that provides 3 basic operations: add_with_priority(), decrease_priority() and extract_min(). As mentioned earlier, using such a data structure can lead to faster computing times than using a basic queue. Notably, Fibonacci heap or Brodal queue offer optimal implementations for those 3 operations. As the algorithm is slightly different in appearance, it is mentioned here, in pseudocode as well:
1 function Dijkstra(Graph, source): 2 create vertex priority queue Q 3 4 dist ← 0 // Initialization 5 Q.add_with_priority(source, 0) // associated priority equals dist 6 7 for each vertex v in Graph.Vertices: 8 if v ≠ source 9 prev ← UNDEFINED // Predecessor of v 10 dist ← INFINITY // Unknown distance from source to v 11 Q.add_with_priority(v, INFINITY) 12 13 14 while Q is not empty: // The main loop 15 u ← Q.extract_min() // Remove and return best vertex 16 for each neighbor v of u: // Go through all v neighbors of u 17 alt ← dist + Graph.Edges(u, v) 18 if alt < dist: 19 prev ← u 20 dist ← alt 21 Q.decrease_priority(v, alt) 22 23 return dist, prev
Instead of filling the priority queue with all nodes in the initialization phase, it is possible to initialize it to contain only source; then, inside the if alt < dist block, the decrease_priority() becomes an add_with_priority() operation.
Yet another alternative is to add nodes unconditionally to the priority queue and to instead check after extraction (u ← Q.extract_min()) that it isn't revisiting, or that no shorter connection was found yet in the if alt < dist block. This can be done by additionally extracting the associated priority p from the queue and only processing further if p == dist inside the while Q is not empty loop.
These alternatives can use entirely array-based priority queues without decrease-key functionality, which have been found to achieve even faster computing times in practice. However, the difference in performance was found to be narrower for denser graphs.
Proof
To prove the correctness of Dijkstra's algorithm, mathematical induction can be used on the number of visited nodes.
Invariant hypothesis: For each visited node v, dist is the shortest distance from source to v, and for each unvisited node u, dist is the shortest distance from source to u when traveling via visited nodes only, or infinity if no such path exists. (Note: we do not assume dist is the actual shortest distance for unvisited nodes, while dist is the actual shortest distance)
Base case
The base case is when there is just one visited node, source. Its distance is defined to be zero, which is the shortest distance, since negative weights are not allowed. Hence, the hypothesis holds.
Induction
Assuming that the hypothesis holds for visited nodes, to show it holds for nodes, let u be the next visited node, i.e. the node with minimum dist. The claim is that dist is the shortest distance from source to u.
The proof is by contradiction. If a shorter path were available, then this shorter path either contains another unvisited node or not.
- In the former case, let w be the first unvisited node on this shorter path. By induction, the shortest paths from source to u and w through visited nodes only have costs
distanddistrespectively. This means the cost of going from source to u via w has the cost of at leastdist+ the minimal cost of going from w to u. As the edge costs are positive, the minimal cost of going from w to u is a positive number. However,distis at mostdistbecause otherwise w would have been picked by the priority queue instead of u. This is a contradiction, since it has already been established thatdist+ a positive number <dist. - In the latter case, let w be the last but one node on the shortest path. That means
dist + Graph.Edges < dist. That is a contradiction because by the time w is visited, it should have setdistto at mostdist + Graph.Edges.
For all other visited nodes v, the dist is already known to be the shortest distance from source already, because of the inductive hypothesis, and these values are unchanged.
After processing u, it is still true that for each unvisited node w, dist is the shortest distance from source to w using visited nodes only. Any shorter path that did not use u, would already have been found, and if a shorter path used u it would have been updated when processing u.
After all nodes are visited, the shortest path from source to any node v consists only of visited nodes. Therefore, dist is the shortest distance.
Running time
Bounds of the running time of Dijkstra's algorithm on a graph with edges E and vertices V can be expressed as a function of the number of edges, denoted , and the number of vertices, denoted , using big-O notation. The complexity bound depends mainly on the data structure used to represent the set Q. In the following, upper bounds can be simplified because is for any simple graph, but that simplification disregards the fact that in some problems, other upper bounds on may hold.
For any data structure for the vertex set Q, the running time i s:
where and are the complexities of the decrease-key and extract-minimum operations in Q, respectively.
The simplest version of Dijkstra's algorithm stores the vertex set Q as a linked list or array, and edges as an adjacency list or matrix. In this case, extract-minimum is simply a linear search through all vertices in Q, so the running time is .
For sparse graphs, that is, graphs with far fewer than edges, Dijkstra's algorithm can be implemented more efficiently by storing the graph in the form of adjacency lists and using a self-balancing binary search tree, binary heap, pairing heap, Fibonacci heap or a priority heap as a priority queue to implement extracting minimum efficiently. To perform decrease-key steps in a binary heap efficiently, it is necessary to use an auxiliary data structure that maps each vertex to its position in the heap, and to update this structure as the priority queue Q changes. With a self-balancing binary search tree or binary heap, the algorithm requires
time in the worst case; for connected graphs this time bound can be simplified to . The Fibonacci heap improves this to
When using binary heaps, the average case time complexity is lower than the worst-case: assuming edge costs are drawn independently from a common probability distribution, the expected number of decrease-key operations is bounded by , giving a total running time of
Practical optimizations and infinite graphs
In common presentations of Dijkstra's algorithm, initially all nodes are entered into the priority queue. This is, however, not necessary: the algorithm can start with a priority queue that contains only one item, and insert new items as they are discovered (instead of doing a decrease-key, check whether the key is in the queue; if it is, decrease its key, otherwise insert it). This variant has the same worst-case bounds as the common variant, but maintains a smaller priority queue in practice, speeding up queue operations.
Moreover, not inserting all nodes in a graph makes it possible to extend the algorithm to find the shortest path from a single source to the closest of a set of target nodes on infinite graphs or those too large to represent in memory. The resulting algorithm is called uniform-cost search (UCS) in the artificial intelligence literature and can be expressed in pseudocode as
procedure uniform_cost_search(start) is
node ← start
frontier ← priority queue containing node only
expanded ← empty set
do
if frontier is empty then
return failure
node ← frontier.pop()
if node is a goal state then
return solution(node)
expanded.add(node)
for each of node's neighbors n do
if n is not in expanded and not in frontier then
frontier.add(n)
else if n is in frontier with higher cost
replace existing node with n
Its complexity can be expressed in an alternative way for very large graphs: when C is the length of the shortest path from the start node to any node satisfying the "goal" predicate, each edge has cost at least ε, and the number of neighbors per node is bounded by b, then the algorithm's worst-case time and space complexity are both in O(b).
Further optimizations for the single-target case include bidirectional variants, goal-directed variants such as the A* algorithm (see § Related problems and algorithms), graph pruning to determine which nodes are likely to form the middle segment of shortest paths (reach-based routing), and hierarchical decompositions of the input graph that reduce s–t routing to connecting s and t to their respective "transit nodes" followed by shortest-path computation between these transit nodes using a "highway". Combinations of such techniques may be needed for optimal practical performance on specific problems.
Optimality for comparison-sorting by distance
As well as simply computing distances and paths, Dijkstra's algorithm can be used to sort vertices by their distances from a given starting vertex. In 2023, Haeupler, Rozhoň, Tětek, Hladík, and Tarjan (one of the inventors of the 1984 heap), proved that, for this sorting problem on a positively-weighted directed graph, a version of Dijkstra's algorithm with a special heap data structure has a runtime and number of comparisons that is within a constant factor of optimal among comparison-based algorithms for the same sorting problem on the same graph and starting vertex but with variable edge weights. To achieve this, they use a comparison-based heap whose cost of returning/removing the minimum element from the heap is logarithmic in the number of elements inserted after it rather than in the number of elements in the heap.
Specialized variants
When arc weights are small integers (bounded by a parameter ), specialized queues can be used for increased speed. The first algorithm of this type was Dial's algorithm for graphs with positive integer edge weights, which uses a bucket queue to obtain a running time . The use of a Van Emde Boas tree as the priority queue brings the complexity to . Another interesting variant based on a combination of a new radix heap and the well-known Fibonacci heap runs in time . Finally, the best algorithms in this special case run in time and time.
Related problems and algorithms
Dijkstra's original algorithm can be extended with modifications. For example, sometimes it is desirable to present solutions which are less than mathematically optimal. To obtain a ranked list of less-than-optimal solutions, the optimal solution is first calculated. A single edge appearing in the optimal solution is removed from the graph, and the optimum solution to this new graph is calculated. Each edge of the original solution is suppressed in turn and a new shortest-path calculated. The secondary solutions are then ranked and presented after the first optimal solution.
Dijkstra's algorithm is usually the working principle behind link-state routing protocols. OSPF and IS-IS are the most common.
Unlike Dijkstra's algorithm, the Bellman–Ford algorithm can be used on graphs with negative edge weights, as long as the graph contains no negative cycle reachable from the source vertex s. The presence of such cycles means that no shortest path can be found, since the label becomes lower each time the cycle is traversed. (This statement assumes that a "path" is allowed to repeat vertices. In graph theory that is normally not allowed. In theoretical computer science it often is allowed.) It is possible to adapt Dijkstra's algorithm to handle negative weights by combining it with the Bellman-Ford algorithm (to remove negative edges and detect negative cycles): Johnson's algorithm.
The A* algorithm is a generalization of Dijkstra's algorithm that reduces the size of the subgraph that must be explored, if additional information is available that provides a lower bound on the distance to the target.
The process that underlies Dijkstra's algorithm is similar to the greedy process used in Prim's algorithm. Prim's purpose is to find a minimum spanning tree that connects all nodes in the graph; Dijkstra is concerned with only two nodes. Prim's does not evaluate the total weight of the path from the starting node, only the individual edges.
Breadth-first search can be viewed as a special-case of Dijkstra's algorithm on unweighted graphs, where the priority queue degenerates into a FIFO queue.
The fast marching method can be viewed as a continuous version of Dijkstra's algorithm which computes the geodesic distance on a triangle mesh.
Dynamic programming perspective
From a dynamic programming point of view, Dijkstra's algorithm is a successive approximation scheme that solves the dynamic programming functional equation for the shortest path problem by the Reaching method.
In fact, Dijkstra's explanation of the logic behind the algorithm:
Problem 2. Find the path of minimum total length between two given nodes P and Q. We use the fact that, if R is a node on the minimal path from P to Q, knowledge of the latter implies the knowledge of the minimal path from P to R.
is a paraphrasing of Bellman's Principle of Optimality in the context of the shortest path problem.
See also
- A* search algorithm
- Bellman–Ford algorithm
- Euclidean shortest path
- Floyd–Warshall algorithm
- Johnson's algorithm
- Longest path problem
- Parallel all-pairs shortest path algorithm
Notes
- Controversial, see Moshe Sniedovich (2006). "Dijkstra's algorithm revisited: the dynamic programming connexion". Control and Cybernetics. 35: 599–620. and below part.
- ^ Cormen et al. 2001.
- ^ Fredman & Tarjan 1987.
- Richards, Hamilton. "Edsger Wybe Dijkstra". A.M. Turing Award. Association for Computing Machinery. Retrieved 16 October 2017.
At the Mathematical Centre a major project was building the ARMAC computer. For its official inauguration in 1956, Dijkstra devised a program to solve a problem interesting to a nontechnical audience: Given a network of roads connecting cities, what is the shortest route between two designated cities?
- ^ Frana, Phil (August 2010). "An Interview with Edsger W. Dijkstra". Communications of the ACM. 53 (8): 41–47. doi:10.1145/1787234.1787249. S2CID 27009702.
- Dijkstra, E. W. (1959). "A note on two problems in connexion with graphs". Numerische Mathematik. 1: 269–271. CiteSeerX 10.1.1.165.7577. doi:10.1007/BF01386390. S2CID 123284777.
- ^ Mehlhorn, Kurt; Sanders, Peter (2008). "Chapter 10. Shortest Paths" (PDF). Algorithms and Data Structures: The Basic Toolbox. Springer. doi:10.1007/978-3-540-77978-0. ISBN 978-3-540-77977-3.
- Schrijver, Alexander (2012). "On the history of the shortest path problem" (PDF). Optimization Stories. Documenta Mathematica Series. Vol. 6. pp. 155–167. doi:10.4171/dms/6/19. ISBN 978-3-936609-58-5.
- Leyzorek et al. 1957.
- Szcześniak, Ireneusz; Jajszczyk, Andrzej; Woźna-Szcześniak, Bożena (2019). "Generic Dijkstra for optical networks". Journal of Optical Communications and Networking. 11 (11): 568–577. arXiv:1810.04481. doi:10.1364/JOCN.11.000568. S2CID 52958911.
- Szcześniak, Ireneusz; Woźna-Szcześniak, Bożena (2023), "Generic Dijkstra: Correctness and tractability", NOMS 2023-2023 IEEE/IFIP Network Operations and Management Symposium, pp. 1–7, arXiv:2204.13547, doi:10.1109/NOMS56928.2023.10154322, ISBN 978-1-6654-7716-1, S2CID 248427020
- ^ Felner, Ariel (2011). Position Paper: Dijkstra's Algorithm versus Uniform Cost Search or a Case Against Dijkstra's Algorithm. Proc. 4th Int'l Symp. on Combinatorial Search. Archived from the original on 18 February 2020. Retrieved 12 February 2015. In a route-finding problem, Felner finds that the queue can be a factor 500–600 smaller, taking some 40% of the running time.
- "ARMAC". Unsung Heroes in Dutch Computing History. 2007. Archived from the original on 13 November 2013.
- Dijkstra, Edsger W., Reflections on "A note on two problems in connexion with graphs (PDF)
- Tarjan, Robert Endre (1983), Data Structures and Network Algorithms, CBMS_NSF Regional Conference Series in Applied Mathematics, vol. 44, Society for Industrial and Applied Mathematics, p. 75,
The third classical minimum spanning tree algorithm was discovered by Jarník and rediscovered by Prim and Dikstra; it is commonly known as Prim's algorithm.
- Prim, R.C. (1957). "Shortest connection networks and some generalizations" (PDF). Bell System Technical Journal. 36 (6): 1389–1401. Bibcode:1957BSTJ...36.1389P. doi:10.1002/j.1538-7305.1957.tb01515.x. Archived from the original (PDF) on 18 July 2017. Retrieved 18 July 2017.
- V. Jarník: O jistém problému minimálním , Práce Moravské Přírodovědecké Společnosti, 6, 1930, pp. 57–63. (in Czech)
- Gass, Saul; Fu, Michael (2013). "Dijkstra's Algorithm". In Gass, Saul I; Fu, Michael C (eds.). Encyclopedia of Operations Research and Management Science. Vol. 1. Springer. doi:10.1007/978-1-4419-1153-7. ISBN 978-1-4419-1137-7 – via Springer Link.
- Fredman & Tarjan 1984.
- Observe that p < dist cannot ever hold because of the update dist ← alt when updating the queue. See https://cs.stackexchange.com/questions/118388/dijkstra-without-decrease-key for discussion.
- Chen, M.; Chowdhury, R. A.; Ramachandran, V.; Roche, D. L.; Tong, L. (2007). Priority Queues and Dijkstra's Algorithm – UTCS Technical Report TR-07-54 – 12 October 2007 (PDF). Austin, Texas: The University of Texas at Austin, Department of Computer Sciences.
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2022) . "22". Introduction to Algorithms (4th ed.). MIT Press and McGraw-Hill. pp. 622–623. ISBN 0-262-04630-X.
- ^ Russell, Stuart; Norvig, Peter (2009) . Artificial Intelligence: A Modern Approach (3rd ed.). Prentice Hall. pp. 75, 81. ISBN 978-0-13-604259-4.
- Sometimes also least-cost-first search: Nau, Dana S. (1983). "Expert computer systems" (PDF). Computer. 16 (2). IEEE: 63–85. doi:10.1109/mc.1983.1654302. S2CID 7301753.
- Wagner, Dorothea; Willhalm, Thomas (2007). Speed-up techniques for shortest-path computations. STACS. pp. 23–36.
- Bauer, Reinhard; Delling, Daniel; Sanders, Peter; Schieferdecker, Dennis; Schultes, Dominik; Wagner, Dorothea (2010). "Combining hierarchical and goal-directed speed-up techniques for Dijkstra's algorithm". J. Experimental Algorithmics. 15: 2.1. doi:10.1145/1671970.1671976. S2CID 1661292.
- Haeupler, Bernhard; Hladík, Richard; Rozhoň, Václav; Tarjan, Robert; Tětek, Jakub (28 October 2024). "Universal Optimality of Dijkstra via Beyond-Worst-Case Heaps". arXiv:2311.11793 .
- Brubaker, Ben (25 October 2024). "Computer Scientists Establish the Best Way to Traverse a Graph". Quanta Magazine. Retrieved 9 December 2024.
- Dial 1969.
- ^ Ahuja et al. 1990.
- Thorup 2000.
- Raman 1997.
- Sniedovich, M. (2006). "Dijkstra's algorithm revisited: the dynamic programming connexion" (PDF). Journal of Control and Cybernetics. 35 (3): 599–620. Online version of the paper with interactive computational modules.
- Denardo, E.V. (2003). Dynamic Programming: Models and Applications. Mineola, NY: Dover Publications. ISBN 978-0-486-42810-9.
- Sniedovich, M. (2010). Dynamic Programming: Foundations and Principles. Francis & Taylor. ISBN 978-0-8247-4099-3.
- Dijkstra 1959, p. 270.
References
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Section 24.3: Dijkstra's algorithm". Introduction to Algorithms (Second ed.). MIT Press and McGraw–Hill. pp. 595–601. ISBN 0-262-03293-7.
- Dial, Robert B. (1969). "Algorithm 360: Shortest-path forest with topological ordering [H]". Communications of the ACM. 12 (11): 632–633. doi:10.1145/363269.363610. S2CID 6754003.
- Fredman, Michael Lawrence; Tarjan, Robert E. (1984). Fibonacci heaps and their uses in improved network optimization algorithms. 25th Annual Symposium on Foundations of Computer Science. IEEE. pp. 338–346. doi:10.1109/SFCS.1984.715934.
- Fredman, Michael Lawrence; Tarjan, Robert E. (1987). "Fibonacci heaps and their uses in improved network optimization algorithms". Journal of the Association for Computing Machinery. 34 (3): 596–615. doi:10.1145/28869.28874. S2CID 7904683.
- Zhan, F. Benjamin; Noon, Charles E. (February 1998). "Shortest Path Algorithms: An Evaluation Using Real Road Networks". Transportation Science. 32 (1): 65–73. doi:10.1287/trsc.32.1.65. S2CID 14986297.
- Leyzorek, M.; Gray, R. S.; Johnson, A. A.; Ladew, W. C.; Meaker, Jr., S. R.; Petry, R. M.; Seitz, R. N. (1957). Investigation of Model Techniques – First Annual Report – 6 June 1956 – 1 July 1957 – A Study of Model Techniques for Communication Systems. Cleveland, Ohio: Case Institute of Technology.
- Knuth, D.E. (1977). "A Generalization of Dijkstra's Algorithm". Information Processing Letters. 6 (1): 1–5. doi:10.1016/0020-0190(77)90002-3.
- Ahuja, Ravindra K.; Mehlhorn, Kurt; Orlin, James B.; Tarjan, Robert E. (April 1990). "Faster Algorithms for the Shortest Path Problem" (PDF). Journal of the ACM. 37 (2): 213–223. doi:10.1145/77600.77615. hdl:1721.1/47994. S2CID 5499589.
- Raman, Rajeev (1997). "Recent results on the single-source shortest paths problem". SIGACT News. 28 (2): 81–87. doi:10.1145/261342.261352. S2CID 18031586.
- Thorup, Mikkel (2000). "On RAM priority Queues". SIAM Journal on Computing. 30 (1): 86–109. doi:10.1137/S0097539795288246. S2CID 5221089.
- Thorup, Mikkel (1999). "Undirected single-source shortest paths with positive integer weights in linear time". Journal of the ACM. 46 (3): 362–394. doi:10.1145/316542.316548. S2CID 207654795.
External links
- Oral history interview with Edsger W. Dijkstra, Charles Babbage Institute, University of Minnesota, Minneapolis
- Implementation of Dijkstra's algorithm using TDD, Robert Cecil Martin, The Clean Code Blog
| Graph and tree traversal algorithms | |
|---|---|
| Search | |
| Shortest path | |
| Minimum spanning tree | |
| List of graph search algorithms | |
| Optimization: Algorithms, methods, and heuristics | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|  | |||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||


 is the number of nodes.
is the number of nodes.  visited nodes, to show it holds for
visited nodes, to show it holds for  nodes, let u be the next visited node, i.e. the node with minimum
nodes, let u be the next visited node, i.e. the node with minimum  , and the number of vertices, denoted
, and the number of vertices, denoted  for any simple graph, but that simplification disregards the fact that in some problems, other upper bounds on
for any simple graph, but that simplification disregards the fact that in some problems, other upper bounds on 
 and
and  are the complexities of the decrease-key and extract-minimum operations in Q, respectively.
are the complexities of the decrease-key and extract-minimum operations in Q, respectively.
 .
.
 edges, Dijkstra's algorithm can be implemented more efficiently by storing the graph in the form of adjacency lists and using a
edges, Dijkstra's algorithm can be implemented more efficiently by storing the graph in the form of adjacency lists and using a 
 . The
. The 
 , giving a total running time of
, giving a total running time of

 ), specialized queues can be used for increased speed. The first algorithm of this type was Dial's algorithm for graphs with positive integer edge weights, which uses a
), specialized queues can be used for increased speed. The first algorithm of this type was Dial's algorithm for graphs with positive integer edge weights, which uses a  . The use of a
. The use of a  . Another interesting variant based on a combination of a new
. Another interesting variant based on a combination of a new  . Finally, the best algorithms in this special case run in
. Finally, the best algorithms in this special case run in  time and
time and  time.
time.
