
In probability theory and machine learning, the multi-armed bandit problem (sometimes called the K- or N-armed bandit problem) is a problem in which a decision maker iteratively selects one of multiple fixed choices (i.e., arms or actions) when the properties of each choice are only partially known at the time of allocation, and may become better understood as time passes. A fundamental aspect of bandit problems is that choosing an arm does not affect the properties of the arm or other arms.
Instances of the multi-armed bandit problem include the task of iteratively allocating a fixed, limited set of resources between competing (alternative) choices in a way that minimizes the regret. A notable alternative setup for the multi-armed bandit problem include the "best arm identification" problem where the goal is instead to identify the best choice by the end of a finite number of rounds.
The multi-armed bandit problem is a classic reinforcement learning problem that exemplifies the exploration–exploitation tradeoff dilemma. In contrast to general RL, the selected actions in bandit problems do not affect the reward distribution of the arms. The name comes from imagining a gambler at a row of slot machines (sometimes known as "one-armed bandits"), who has to decide which machines to play, how many times to play each machine and in which order to play them, and whether to continue with the current machine or try a different machine. The multi-armed bandit problem also falls into the broad category of stochastic scheduling.
In the problem, each machine provides a random reward from a probability distribution specific to that machine, that is not known a priori. The objective of the gambler is to maximize the sum of rewards earned through a sequence of lever pulls. The crucial tradeoff the gambler faces at each trial is between "exploitation" of the machine that has the highest expected payoff and "exploration" to get more information about the expected payoffs of the other machines. The trade-off between exploration and exploitation is also faced in machine learning. In practice, multi-armed bandits have been used to model problems such as managing research projects in a large organization, like a science foundation or a pharmaceutical company. In early versions of the problem, the gambler begins with no initial knowledge about the machines.
Herbert Robbins in 1952, realizing the importance of the problem, constructed convergent population selection strategies in "some aspects of the sequential design of experiments". A theorem, the Gittins index, first published by John C. Gittins, gives an optimal policy for maximizing the expected discounted reward.
Empirical motivation

The multi-armed bandit problem models an agent that simultaneously attempts to acquire new knowledge (called "exploration") and optimize their decisions based on existing knowledge (called "exploitation"). The agent attempts to balance these competing tasks in order to maximize their total value over the period of time considered. There are many practical applications of the bandit model, for example:
- clinical trials investigating the effects of different experimental treatments while minimizing patient losses,
- adaptive routing efforts for minimizing delays in a network,
- financial portfolio design
In these practical examples, the problem requires balancing reward maximization based on the knowledge already acquired with attempting new actions to further increase knowledge. This is known as the exploitation vs. exploration tradeoff in machine learning.
The model has also been used to control dynamic allocation of resources to different projects, answering the question of which project to work on, given uncertainty about the difficulty and payoff of each possibility.
Originally considered by Allied scientists in World War II, it proved so intractable that, according to Peter Whittle, the problem was proposed to be dropped over Germany so that German scientists could also waste their time on it.
The version of the problem now commonly analyzed was formulated by Herbert Robbins in 1952.
The multi-armed bandit model
The multi-armed bandit (short: bandit or MAB) can be seen as a set of real distributions , each distribution being associated with the rewards delivered by one of the levers. Let be the mean values associated with these reward distributions. The gambler iteratively plays one lever per round and observes the associated reward. The objective is to maximize the sum of the collected rewards. The horizon is the number of rounds that remain to be played. The bandit problem is formally equivalent to a one-state Markov decision process. The regret after rounds is defined as the expected difference between the reward sum associated with an optimal strategy and the sum of the collected rewards:
,
where is the maximal reward mean, , and is the reward in round t.
A zero-regret strategy is a strategy whose average regret per round tends to zero with probability 1 when the number of played rounds tends to infinity. Intuitively, zero-regret strategies are guaranteed to converge to a (not necessarily unique) optimal strategy if enough rounds are played.
Variations
A common formulation is the Binary multi-armed bandit or Bernoulli multi-armed bandit, which issues a reward of one with probability , and otherwise a reward of zero.
Another formulation of the multi-armed bandit has each arm representing an independent Markov machine. Each time a particular arm is played, the state of that machine advances to a new one, chosen according to the Markov state evolution probabilities. There is a reward depending on the current state of the machine. In a generalization called the "restless bandit problem", the states of non-played arms can also evolve over time. There has also been discussion of systems where the number of choices (about which arm to play) increases over time.
Computer science researchers have studied multi-armed bandits under worst-case assumptions, obtaining algorithms to minimize regret in both finite and infinite (asymptotic) time horizons for both stochastic and non-stochastic arm payoffs.
Best Arm Identification
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (August 2024) (Learn how and when to remove this message) |
An important variation of the classical regret minimization problem in multi-armed bandits is the one of Best Arm Identification (BAI), also known as pure exploration. This problem is crucial in various applications, including clinical trials, adaptive routing, recommendation systems, and A/B testing.
In BAI, the objective is to identify the arm having the highest expected reward. An algorithm in this setting is characterized by a sampling rule, a decision rule, and a stopping rule, described as follows:
- Sampling rule: is a sequence of actions at each time step
- Stopping rule: is a (random) stopping time which suggests when to stop collecting samples
- Decision rule: is a guess on the best arm based on the data collected up to time
There are two predominant settings in BAI:
Fixed budget setting: Given a time horizon , the objective is to identify the arm with the highest expected reward minimizing probability of error .
Fixed confidence setting: Given a confidence level , the objective is to identify the arm with the highest expected reward with the least possible amount of trials and with probability of error .
For example using a decision rule, we could use where is the machine no.1 (you can use a different variable respectively) and is the amount for each time an attempt is made at pulling the lever, where , identify as the sum of each attempts , (...) as needed, and from there you can get a ratio, sum or mean as quantitative probability and sample your formulation for each slots.
You can also do where equal to each a unique machine slot, is the amount each time the lever is triggered, is the sum of , would be the total available amount in your possession, is relative to where reduced as the sum of each gain or loss from (let's say you have 100$ that is defined as and would be a gain is equal to a loss, from there you get your results either positive or negative to add for with your own specific rule) and as the maximum you are willing to spend. It is possible to express this construction using a combination of multiple algebraic formulation, as mentioned above where you can limit with for, or in Time and so on.
Bandit strategies
A major breakthrough was the construction of optimal population selection strategies, or policies (that possess uniformly maximum convergence rate to the population with highest mean) in the work described below.
Optimal solutions
Further information: Gittins indexIn the paper "Asymptotically efficient adaptive allocation rules", Lai and Robbins (following papers of Robbins and his co-workers going back to Robbins in the year 1952) constructed convergent population selection policies that possess the fastest rate of convergence (to the population with highest mean) for the case that the population reward distributions are the one-parameter exponential family. Then, in Katehakis and Robbins simplifications of the policy and the main proof were given for the case of normal populations with known variances. The next notable progress was obtained by Burnetas and Katehakis in the paper "Optimal adaptive policies for sequential allocation problems", where index based policies with uniformly maximum convergence rate were constructed, under more general conditions that include the case in which the distributions of outcomes from each population depend on a vector of unknown parameters. Burnetas and Katehakis (1996) also provided an explicit solution for the important case in which the distributions of outcomes follow arbitrary (i.e., non-parametric) discrete, univariate distributions.
Later in "Optimal adaptive policies for Markov decision processes" Burnetas and Katehakis studied the much larger model of Markov Decision Processes under partial information, where the transition law and/or the expected one period rewards may depend on unknown parameters. In this work, the authors constructed an explicit form for a class of adaptive policies with uniformly maximum convergence rate properties for the total expected finite horizon reward under sufficient assumptions of finite state-action spaces and irreducibility of the transition law. A main feature of these policies is that the choice of actions, at each state and time period, is based on indices that are inflations of the right-hand side of the estimated average reward optimality equations. These inflations have recently been called the optimistic approach in the work of Tewari and Bartlett, Ortner Filippi, Cappé, and Garivier, and Honda and Takemura.
For Bernoulli multi-armed bandits, Pilarski et al. studied computation methods of deriving fully optimal solutions (not just asymptotically) using dynamic programming in the paper "Optimal Policy for Bernoulli Bandits: Computation and Algorithm Gauge." Via indexing schemes, lookup tables, and other techniques, this work provided practically applicable optimal solutions for Bernoulli bandits provided that time horizons and numbers of arms did not become excessively large. Pilarski et al. later extended this work in "Delayed Reward Bernoulli Bandits: Optimal Policy and Predictive Meta-Algorithm PARDI" to create a method of determining the optimal policy for Bernoulli bandits when rewards may not be immediately revealed following a decision and may be delayed. This method relies upon calculating expected values of reward outcomes which have not yet been revealed and updating posterior probabilities when rewards are revealed.
When optimal solutions to multi-arm bandit tasks are used to derive the value of animals' choices, the activity of neurons in the amygdala and ventral striatum encodes the values derived from these policies, and can be used to decode when the animals make exploratory versus exploitative choices. Moreover, optimal policies better predict animals' choice behavior than alternative strategies (described below). This suggests that the optimal solutions to multi-arm bandit problems are biologically plausible, despite being computationally demanding.
Approximate solutions
Many strategies exist which provide an approximate solution to the bandit problem, and can be put into the four broad categories detailed below.
Semi-uniform strategies
Semi-uniform strategies were the earliest (and simplest) strategies discovered to approximately solve the bandit problem. All those strategies have in common a greedy behavior where the best lever (based on previous observations) is always pulled except when a (uniformly) random action is taken.
- Epsilon-greedy strategy: The best lever is selected for a proportion of the trials, and a lever is selected at random (with uniform probability) for a proportion . A typical parameter value might be , but this can vary widely depending on circumstances and predilections.
- Epsilon-first strategy: A pure exploration phase is followed by a pure exploitation phase. For trials in total, the exploration phase occupies trials and the exploitation phase trials. During the exploration phase, a lever is randomly selected (with uniform probability); during the exploitation phase, the best lever is always selected.
- Epsilon-decreasing strategy: Similar to the epsilon-greedy strategy, except that the value of decreases as the experiment progresses, resulting in highly explorative behaviour at the start and highly exploitative behaviour at the finish.
- Adaptive epsilon-greedy strategy based on value differences (VDBE): Similar to the epsilon-decreasing strategy, except that epsilon is reduced on basis of the learning progress instead of manual tuning (Tokic, 2010). High fluctuations in the value estimates lead to a high epsilon (high exploration, low exploitation); low fluctuations to a low epsilon (low exploration, high exploitation). Further improvements can be achieved by a softmax-weighted action selection in case of exploratory actions (Tokic & Palm, 2011).
- Adaptive epsilon-greedy strategy based on Bayesian ensembles (Epsilon-BMC): An adaptive epsilon adaptation strategy for reinforcement learning similar to VBDE, with monotone convergence guarantees. In this framework, the epsilon parameter is viewed as the expectation of a posterior distribution weighting a greedy agent (that fully trusts the learned reward) and uniform learning agent (that distrusts the learned reward). This posterior is approximated using a suitable Beta distribution under the assumption of normality of observed rewards. In order to address the possible risk of decreasing epsilon too quickly, uncertainty in the variance of the learned reward is also modeled and updated using a normal-gamma model. (Gimelfarb et al., 2019).
Probability matching strategies
Probability matching strategies reflect the idea that the number of pulls for a given lever should match its actual probability of being the optimal lever. Probability matching strategies are also known as Thompson sampling or Bayesian Bandits, and are surprisingly easy to implement if you can sample from the posterior for the mean value of each alternative.
Probability matching strategies also admit solutions to so-called contextual bandit problems.
Pricing strategies
Pricing strategies establish a price for each lever. For example, as illustrated with the POKER algorithm, the price can be the sum of the expected reward plus an estimation of extra future rewards that will gain through the additional knowledge. The lever of highest price is always pulled.
Contextual bandit
A useful generalization of the multi-armed bandit is the contextual multi-armed bandit. At each iteration an agent still has to choose between arms, but they also see a d-dimensional feature vector, the context vector they can use together with the rewards of the arms played in the past to make the choice of the arm to play. Over time, the learner's aim is to collect enough information about how the context vectors and rewards relate to each other, so that it can predict the next best arm to play by looking at the feature vectors.
Approximate solutions for contextual bandit
Many strategies exist that provide an approximate solution to the contextual bandit problem, and can be put into two broad categories detailed below.
Online linear bandits
- LinUCB (Upper Confidence Bound) algorithm: the authors assume a linear dependency between the expected reward of an action and its context and model the representation space using a set of linear predictors.
- LinRel (Linear Associative Reinforcement Learning) algorithm: Similar to LinUCB, but utilizes Singular-value decomposition rather than Ridge regression to obtain an estimate of confidence.
Online non-linear bandits
- UCBogram algorithm: The nonlinear reward functions are estimated using a piecewise constant estimator called a regressogram in nonparametric regression. Then, UCB is employed on each constant piece. Successive refinements of the partition of the context space are scheduled or chosen adaptively.
- Generalized linear algorithms: The reward distribution follows a generalized linear model, an extension to linear bandits.
- KernelUCB algorithm: a kernelized non-linear version of linearUCB, with efficient implementation and finite-time analysis.
- Bandit Forest algorithm: a random forest is built and analyzed w.r.t the random forest built knowing the joint distribution of contexts and rewards.
- Oracle-based algorithm: The algorithm reduces the contextual bandit problem into a series of supervised learning problem, and does not rely on typical realizability assumption on the reward function.
Constrained contextual bandit
In practice, there is usually a cost associated with the resource consumed by each action and the total cost is limited by a budget in many applications such as crowdsourcing and clinical trials. Constrained contextual bandit (CCB) is such a model that considers both the time and budget constraints in a multi-armed bandit setting. A. Badanidiyuru et al. first studied contextual bandits with budget constraints, also referred to as Resourceful Contextual Bandits, and show that a regret is achievable. However, their work focuses on a finite set of policies, and the algorithm is computationally inefficient.
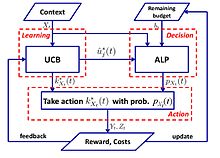
A simple algorithm with logarithmic regret is proposed in:
- UCB-ALP algorithm: The framework of UCB-ALP is shown in the right figure. UCB-ALP is a simple algorithm that combines the UCB method with an Adaptive Linear Programming (ALP) algorithm, and can be easily deployed in practical systems. It is the first work that show how to achieve logarithmic regret in constrained contextual bandits. Although is devoted to a special case with single budget constraint and fixed cost, the results shed light on the design and analysis of algorithms for more general CCB problems.
Adversarial bandit
Another variant of the multi-armed bandit problem is called the adversarial bandit, first introduced by Auer and Cesa-Bianchi (1998). In this variant, at each iteration, an agent chooses an arm and an adversary simultaneously chooses the payoff structure for each arm. This is one of the strongest generalizations of the bandit problem as it removes all assumptions of the distribution and a solution to the adversarial bandit problem is a generalized solution to the more specific bandit problems.
Example: Iterated prisoner's dilemma
An example often considered for adversarial bandits is the iterated prisoner's dilemma. In this example, each adversary has two arms to pull. They can either Deny or Confess. Standard stochastic bandit algorithms don't work very well with these iterations. For example, if the opponent cooperates in the first 100 rounds, defects for the next 200, then cooperate in the following 300, etc. then algorithms such as UCB won't be able to react very quickly to these changes. This is because after a certain point sub-optimal arms are rarely pulled to limit exploration and focus on exploitation. When the environment changes the algorithm is unable to adapt or may not even detect the change.
Approximate solutions
Exp3
EXP3 is a popular algorithm for adversarial multiarmed bandits, suggested and analyzed in this setting by Auer et al. . Recently there was an increased interest in the performance of this algorithm in the stochastic setting, due to its new applications to stochastic multi-armed bandits with side information and to multi-armed bandits in the mixed stochastic-adversarial setting . The paper presented an empirical evaluation and improved analysis of the performance of the EXP3 algorithm in the stochastic setting, as well as a modification of the EXP3 algorithm capable of achieving "logarithmic" regret in stochastic environment.
Algorithm
Parameters: Real Initialisation: for For each t = 1, 2, ..., T 1. Set 2. Draw randomly according to the probabilities 3. Receive reward 4. For set:
Explanation
Exp3 chooses an arm at random with probability it prefers arms with higher weights (exploit), it chooses with probability to uniformly randomly explore. After receiving the rewards the weights are updated. The exponential growth significantly increases the weight of good arms.
Regret analysis
The (external) regret of the Exp3 algorithm is at most
Follow the perturbed leader (FPL) algorithm
Algorithm
Parameters: Real Initialisation: For each t = 1,2,...,T 1. For each arm generate a random noise from an exponential distribution 2. Pull arm : Add noise to each arm and pull the one with the highest value 3. Update value: The rest remains the same
Explanation
We follow the arm that we think has the best performance so far adding exponential noise to it to provide exploration.
Exp3 vs FPL
| Exp3 | FPL |
|---|---|
| Maintains weights for each arm to calculate pulling probability | Doesn't need to know the pulling probability per arm |
| Has efficient theoretical guarantees | The standard FPL does not have good theoretical guarantees |
| Might be computationally expensive (calculating the exponential terms) | Computationally quite efficient |
Infinite-armed bandit
In the original specification and in the above variants, the bandit problem is specified with a discrete and finite number of arms, often indicated by the variable . In the infinite armed case, introduced by Agrawal (1995), the "arms" are a continuous variable in dimensions.
Non-stationary bandit
This framework refers to the multi-armed bandit problem in a non-stationary setting (i.e., in presence of concept drift). In the non-stationary setting, it is assumed that the expected reward for an arm can change at every time step : . Thus, no longer represents the whole sequence of expected (stationary) rewards for arm . Instead, denotes the sequence of expected rewards for arm , defined as .
A dynamic oracle represents the optimal policy to be compared with other policies in the non-stationary setting. The dynamic oracle optimises the expected reward at each step by always selecting the best arm, with expected reward of . Thus, the cumulative expected reward for the dynamic oracle at final time step is defined as:
Hence, the regret for policy is computed as the difference between and the cumulative expected reward at step for policy :
Garivier and Moulines derive some of the first results with respect to bandit problems where the underlying model can change during play. A number of algorithms were presented to deal with this case, including Discounted UCB and Sliding-Window UCB. A similar approach based on Thompson Sampling algorithm is the f-Discounted-Sliding-Window Thompson Sampling (f-dsw TS) proposed by Cavenaghi et al. The f-dsw TS algorithm exploits a discount factor on the reward history and an arm-related sliding window to contrast concept drift in non-stationary environments. Another work by Burtini et al. introduces a weighted least squares Thompson sampling approach (WLS-TS), which proves beneficial in both the known and unknown non-stationary cases.
Other variants
Many variants of the problem have been proposed in recent years.
Dueling bandit
The dueling bandit variant was introduced by Yue et al. (2012) to model the exploration-versus-exploitation tradeoff for relative feedback. In this variant the gambler is allowed to pull two levers at the same time, but they only get a binary feedback telling which lever provided the best reward. The difficulty of this problem stems from the fact that the gambler has no way of directly observing the reward of their actions. The earliest algorithms for this problem are InterleaveFiltering, Beat-The-Mean. The relative feedback of dueling bandits can also lead to voting paradoxes. A solution is to take the Condorcet winner as a reference.
More recently, researchers have generalized algorithms from traditional MAB to dueling bandits: Relative Upper Confidence Bounds (RUCB), Relative EXponential weighing (REX3), Copeland Confidence Bounds (CCB), Relative Minimum Empirical Divergence (RMED), and Double Thompson Sampling (DTS).
Collaborative bandit
Approaches using multiple bandits that cooperate sharing knowledge in order to better optimize their performance started in 2013 with "A Gang of Bandits", an algorithm relying on a similarity graph between the different bandit problems to share knowledge. The need of a similarity graph was removed in 2014 by the work on the CLUB algorithm. Following this work, several other researchers created algorithms to learn multiple models at the same time under bandit feedback. For example, COFIBA was introduced by Li and Karatzoglou and Gentile (SIGIR 2016), where the classical collaborative filtering, and content-based filtering methods try to learn a static recommendation model given training data.
Combinatorial bandit
The Combinatorial Multiarmed Bandit (CMAB) problem arises when instead of a single discrete variable to choose from, an agent needs to choose values for a set of variables. Assuming each variable is discrete, the number of possible choices per iteration is exponential in the number of variables. Several CMAB settings have been studied in the literature, from settings where the variables are binary to more general setting where each variable can take an arbitrary set of values.
See also
- Gittins index – a powerful, general strategy for analyzing bandit problems.
- Greedy algorithm
- Optimal stopping
- Search theory
- Stochastic scheduling
References
- ^ Auer, P.; Cesa-Bianchi, N.; Fischer, P. (2002). "Finite-time Analysis of the Multiarmed Bandit Problem". Machine Learning. 47 (2/3): 235–256. doi:10.1023/A:1013689704352.
- Katehakis, Michael N.; Veinott, Jr., Arthur F. (1987). "The Multi-Armed Bandit Problem: Decomposition and Computation". Mathematics of Operations Research. 12 (2): 262–268. doi:10.1287/moor.12.2.262. S2CID 656323.
- Bubeck, Sébastien (2012). "Regret Analysis of Stochastic and Nonstochastic Multi-armed Bandit Problems". Foundations and Trends in Machine Learning. 5: 1–122. arXiv:1204.5721. doi:10.1561/2200000024.
- ^ Gittins, J. C. (1989), Multi-armed bandit allocation indices, Wiley-Interscience Series in Systems and Optimization., Chichester: John Wiley & Sons, Ltd., ISBN 978-0-471-92059-5
- ^ Berry, Donald A.; Fristedt, Bert (1985), Bandit problems: Sequential allocation of experiments, Monographs on Statistics and Applied Probability, London: Chapman & Hall, ISBN 978-0-412-24810-8
- Soare, Marta; Lazaric, Alessandro; Munos, Rémi (2014). "Best-Arm Identification in Linear Bandits". arXiv:1409.6110 .
- Weber, Richard (1992), "On the Gittins index for multiarmed bandits", Annals of Applied Probability, 2 (4): 1024–1033, doi:10.1214/aoap/1177005588, JSTOR 2959678
- Robbins, H. (1952). "Some aspects of the sequential design of experiments". Bulletin of the American Mathematical Society. 58 (5): 527–535. doi:10.1090/S0002-9904-1952-09620-8.
- J. C. Gittins (1979). "Bandit Processes and Dynamic Allocation Indices". Journal of the Royal Statistical Society. Series B (Methodological). 41 (2): 148–177. doi:10.1111/j.2517-6161.1979.tb01068.x. JSTOR 2985029. S2CID 17724147.
- Press, William H. (2009), "Bandit solutions provide unified ethical models for randomized clinical trials and comparative effectiveness research", Proceedings of the National Academy of Sciences, 106 (52): 22387–22392, Bibcode:2009PNAS..10622387P, doi:10.1073/pnas.0912378106, PMC 2793317, PMID 20018711.
- Press (1986)
- Brochu, Eric; Hoffman, Matthew W.; de Freitas, Nando (September 2010). "Portfolio Allocation for Bayesian Optimization". arXiv:1009.5419 .
- Shen, Weiwei; Wang, Jun; Jiang, Yu-Gang; Zha, Hongyuan (2015), "Portfolio Choices with Orthogonal Bandit Learning", Proceedings of International Joint Conferences on Artificial Intelligence (IJCAI2015), archived from the original on 2021-12-04, retrieved 2016-03-20
- Farias, Vivek F; Ritesh, Madan (2011), "The irrevocable multiarmed bandit problem", Operations Research, 59 (2): 383–399, CiteSeerX 10.1.1.380.6983, doi:10.1287/opre.1100.0891
- Whittle, Peter (1979), "Discussion of Dr Gittins' paper", Journal of the Royal Statistical Society, Series B, 41 (2): 148–177, doi:10.1111/j.2517-6161.1979.tb01069.x
- ^ Vermorel, Joannes; Mohri, Mehryar (2005), Multi-armed bandit algorithms and empirical evaluation (PDF), In European Conference on Machine Learning, Springer, pp. 437–448
- Whittle, Peter (1988), "Restless bandits: Activity allocation in a changing world", Journal of Applied Probability, 25A: 287–298, doi:10.2307/3214163, JSTOR 3214163, MR 0974588, S2CID 202109695
- Whittle, Peter (1981), "Arm-acquiring bandits", Annals of Probability, 9 (2): 284–292, doi:10.1214/aop/1176994469
- Auer, P.; Cesa-Bianchi, N.; Freund, Y.; Schapire, R. E. (2002). "The Nonstochastic Multiarmed Bandit Problem". SIAM J. Comput. 32 (1): 48–77. CiteSeerX 10.1.1.130.158. doi:10.1137/S0097539701398375. S2CID 13209702.
- Aurelien Garivier; Emilie Kaufmann (2016). "Optimal Best Arm Identification with Fixed Confidence". arXiv:1602.04589 .
- Lai, T.L.; Robbins, H. (1985). "Asymptotically efficient adaptive allocation rules". Advances in Applied Mathematics. 6 (1): 4–22. doi:10.1016/0196-8858(85)90002-8.
- Katehakis, M.N.; Robbins, H. (1995). "Sequential choice from several populations". Proceedings of the National Academy of Sciences of the United States of America. 92 (19): 8584–5. Bibcode:1995PNAS...92.8584K. doi:10.1073/pnas.92.19.8584. PMC 41010. PMID 11607577.
- Burnetas, A.N.; Katehakis, M.N. (1996). "Optimal adaptive policies for sequential allocation problems". Advances in Applied Mathematics. 17 (2): 122–142. doi:10.1006/aama.1996.0007.
- Burnetas, Apostolos N.; Katehakis, Michael N. (1997). "Optimal adaptive policies for Markov decision processes". Mathematics of Operations Research. 22 (1): 222–255. doi:10.1287/moor.22.1.222.
- Tewari, A.; Bartlett, P.L. (2008). "Optimistic linear programming gives logarithmic regret for irreducible MDPs" (PDF). Advances in Neural Information Processing Systems. 20. CiteSeerX 10.1.1.69.5482. Archived from the original (PDF) on 2012-05-25. Retrieved 2012-10-12.
- Ortner, R. (2010). "Online regret bounds for Markov decision processes with deterministic transitions". Theoretical Computer Science. 411 (29): 2684–2695. doi:10.1016/j.tcs.2010.04.005.
- Filippi, S. and Cappé, O. and Garivier, A. (2010). "Online regret bounds for Markov decision processes with deterministic transitions", Communication, Control, and Computing (Allerton), 2010 48th Annual Allerton Conference on, pp. 115–122
- Honda, J.; Takemura, A. (2011). "An asymptotically optimal policy for finite support models in the multi-armed bandit problem". Machine Learning. 85 (3): 361–391. arXiv:0905.2776. doi:10.1007/s10994-011-5257-4. S2CID 821462.
- ^ Pilarski, Sebastian; Pilarski, Slawomir; Varró, Dániel (February 2021). "Optimal Policy for Bernoulli Bandits: Computation and Algorithm Gauge". IEEE Transactions on Artificial Intelligence. 2 (1): 2–17. doi:10.1109/TAI.2021.3074122. ISSN 2691-4581. S2CID 235475602.
- ^ Pilarski, Sebastian; Pilarski, Slawomir; Varro, Daniel (2021). "Delayed Reward Bernoulli Bandits: Optimal Policy and Predictive Meta-Algorithm PARDI". IEEE Transactions on Artificial Intelligence. 3 (2): 152–163. doi:10.1109/TAI.2021.3117743. ISSN 2691-4581. S2CID 247682940.
- Averbeck, B.B. (2015). "Theory of choice in bandit, information sampling, and foraging tasks". PLOS Computational Biology. 11 (3): e1004164. Bibcode:2015PLSCB..11E4164A. doi:10.1371/journal.pcbi.1004164. PMC 4376795. PMID 25815510.
- Costa, V.D.; Averbeck, B.B. (2019). "Subcortical Substrates of Explore-Exploit Decisions in Primates". Neuron. 103 (3): 533–535. doi:10.1016/j.neuron.2019.05.017. PMC 6687547. PMID 31196672.
- Sutton, R. S. & Barto, A. G. 1998 Reinforcement learning: an introduction. Cambridge, MA: MIT Press.
- Tokic, Michel (2010), "Adaptive ε-greedy exploration in reinforcement learning based on value differences" (PDF), KI 2010: Advances in Artificial Intelligence, Lecture Notes in Computer Science, vol. 6359, Springer-Verlag, pp. 203–210, CiteSeerX 10.1.1.458.464, doi:10.1007/978-3-642-16111-7_23, ISBN 978-3-642-16110-0.
- Tokic, Michel; Palm, Günther (2011), "Value-Difference Based Exploration: Adaptive Control Between Epsilon-Greedy and Softmax" (PDF), KI 2011: Advances in Artificial Intelligence, Lecture Notes in Computer Science, vol. 7006, Springer-Verlag, pp. 335–346, ISBN 978-3-642-24455-1.
- Gimelfarb, Michel; Sanner, Scott; Lee, Chi-Guhn (2019), "ε-BMC: A Bayesian Ensemble Approach to Epsilon-Greedy Exploration in Model-Free Reinforcement Learning" (PDF), Proceedings of the Thirty-Fifth Conference on Uncertainty in Artificial Intelligence, AUAI Press, p. 162.
- ^ Scott, S.L. (2010), "A modern Bayesian look at the multi-armed bandit", Applied Stochastic Models in Business and Industry, 26 (2): 639–658, doi:10.1002/asmb.874, S2CID 573750
- Olivier Chapelle; Lihong Li (2011), "An empirical evaluation of Thompson sampling", Advances in Neural Information Processing Systems, 24, Curran Associates: 2249–2257
- Langford, John; Zhang, Tong (2008), "The Epoch-Greedy Algorithm for Contextual Multi-armed Bandits", Advances in Neural Information Processing Systems, vol. 20, Curran Associates, Inc., pp. 817–824
- Lihong Li; Wei Chu; John Langford; Robert E. Schapire (2010), "A contextual-bandit approach to personalized news article recommendation", Proceedings of the 19th international conference on World wide web, pp. 661–670, arXiv:1003.0146, doi:10.1145/1772690.1772758, ISBN 9781605587998, S2CID 207178795
- Wei Chu; Lihong Li; Lev Reyzin; Robert E. Schapire (2011), "Contextual bandits with linear payoff functions" (PDF), Proceedings of the 14th International Conference on Artificial Intelligence and Statistics (AISTATS): 208–214
- Auer, P. (2000). "Using upper confidence bounds for online learning". Proceedings 41st Annual Symposium on Foundations of Computer Science. IEEE Comput. Soc. pp. 270–279. doi:10.1109/sfcs.2000.892116. ISBN 978-0769508504. S2CID 28713091.
- Hong, Tzung-Pei; Song, Wei-Ping; Chiu, Chu-Tien (November 2011). "Evolutionary Composite Attribute Clustering". 2011 International Conference on Technologies and Applications of Artificial Intelligence. IEEE. pp. 305–308. doi:10.1109/taai.2011.59. ISBN 9781457721748. S2CID 14125100.
- Rigollet, Philippe; Zeevi, Assaf (2010), Nonparametric Bandits with Covariates, Conference on Learning Theory, COLT 2010, arXiv:1003.1630, Bibcode:2010arXiv1003.1630R
- Slivkins, Aleksandrs (2011), Contextual bandits with similarity information. (PDF), Conference on Learning Theory, COLT 2011
- Perchet, Vianney; Rigollet, Philippe (2013), "The multi-armed bandit problem with covariates", Annals of Statistics, 41 (2): 693–721, arXiv:1110.6084, doi:10.1214/13-aos1101, S2CID 14258665
- Sarah Filippi; Olivier Cappé; Aurélien Garivier; Csaba Szepesvári (2010), "Parametric Bandits: The Generalized Linear Case", Advances in Neural Information Processing Systems, 23, Curran Associates: 586–594
- Lihong Li; Yu Lu; Dengyong Zhou (2017), "Provably optimal algorithms for generalized linear contextual bandits", Proceedings of the 34th International Conference on Machine Learning (ICML): 2071–2080, arXiv:1703.00048, Bibcode:2017arXiv170300048L
- Kwang-Sung Jun; Aniruddha Bhargava; Robert D. Nowak; Rebecca Willett (2017), "Scalable generalized linear bandits: Online computation and hashing", Advances in Neural Information Processing Systems, 30, Curran Associates: 99–109, arXiv:1706.00136, Bibcode:2017arXiv170600136J
- Branislav Kveton; Manzil Zaheer; Csaba Szepesvári; Lihong Li; Mohammad Ghavamzadeh; Craig Boutilier (2020), "Randomized exploration in generalized linear bandits", Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics (AISTATS), arXiv:1906.08947, Bibcode:2019arXiv190608947K
- Michal Valko; Nathan Korda; Rémi Munos; Ilias Flaounas; Nello Cristianini (2013), Finite-Time Analysis of Kernelised Contextual Bandits, 29th Conference on Uncertainty in Artificial Intelligence (UAI 2013) and (JFPDA 2013)., arXiv:1309.6869, Bibcode:2013arXiv1309.6869V
- Féraud, Raphaël; Allesiardo, Robin; Urvoy, Tanguy; Clérot, Fabrice (2016). "Random Forest for the Contextual Bandit Problem". Aistats: 93–101. Archived from the original on 2016-08-10. Retrieved 2016-06-10.
- Alekh Agarwal; Daniel J. Hsu; Satyen Kale; John Langford; Lihong Li; Robert E. Schapire (2014), "Taming the monster: A fast and simple algorithm for contextual bandits", Proceedings of the 31st International Conference on Machine Learning (ICML): 1638–1646, arXiv:1402.0555, Bibcode:2014arXiv1402.0555A
- Badanidiyuru, A.; Langford, J.; Slivkins, A. (2014), "Resourceful contextual bandits" (PDF), Proceeding of Conference on Learning Theory (COLT)
- ^ Wu, Huasen; Srikant, R.; Liu, Xin; Jiang, Chong (2015), "Algorithms with Logarithmic or Sublinear Regret for Constrained Contextual Bandits", The 29th Annual Conference on Neural Information Processing Systems (NIPS), 28, Curran Associates: 433–441, arXiv:1504.06937, Bibcode:2015arXiv150406937W
- Burtini, Giuseppe; Loeppky, Jason; Lawrence, Ramon (2015). "A Survey of Online Experiment Design with the Stochastic Multi-Armed Bandit". arXiv:1510.00757 .
- Seldin, Y., Szepesvári, C., Auer, P. and Abbasi-Yadkori, Y., 2012, December. Evaluation and Analysis of the Performance of the EXP3 Algorithm in Stochastic Environments. In EWRL (pp. 103–116).
- Hutter, M. and Poland, J., 2005. Adaptive online prediction by following the perturbed leader. Journal of Machine Learning Research, 6 (Apr), pp.639–660.
- Agrawal, Rajeev. The Continuum-Armed Bandit Problem. SIAM J. of Control and Optimization. 1995.
- Besbes, O.; Gur, Y.; Zeevi, A. Stochastic multi-armed-bandit problem with non-stationary rewards. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 199–207<https://proceedings.neurips.cc/paper/2014/file/903ce9225fca3e988c2af215d4e544d3-Paper.pdf>
- Discounted UCB, Levente Kocsis, Csaba Szepesvári, 2006
- Garivier, Aurélien; Moulines, Eric (2008). "On Upper-Confidence Bound Policies for Non-Stationary Bandit Problems". arXiv:0805.3415 .
- Cavenaghi, Emanuele; Sottocornola, Gabriele; Stella, Fabio; Zanker, Markus (2021). "Non Stationary Multi-Armed Bandit: Empirical Evaluation of a New Concept Drift-Aware Algorithm". Entropy. 23 (3): 380. Bibcode:2021Entrp..23..380C. doi:10.3390/e23030380. PMC 8004723. PMID 33807028.
- Improving Online Marketing Experiments with Drifting Multi-armed Bandits, Giuseppe Burtini, Jason Loeppky, Ramon Lawrence, 2015 <http://www.scitepress.org/DigitalLibrary/PublicationsDetail.aspx?ID=Dx2xXEB0PJE=&t=1>
- ^ Yue, Yisong; Broder, Josef; Kleinberg, Robert; Joachims, Thorsten (2012), "The K-armed dueling bandits problem", Journal of Computer and System Sciences, 78 (5): 1538–1556, CiteSeerX 10.1.1.162.2764, doi:10.1016/j.jcss.2011.12.028
- Yue, Yisong; Joachims, Thorsten (2011), "Beat the Mean Bandit", Proceedings of ICML'11
- Urvoy, Tanguy; Clérot, Fabrice; Féraud, Raphaël; Naamane, Sami (2013), "Generic Exploration and K-armed Voting Bandits" (PDF), Proceedings of the 30th International Conference on Machine Learning (ICML-13), archived from the original (PDF) on 2016-10-02, retrieved 2016-04-29
- Zoghi, Masrour; Whiteson, Shimon; Munos, Remi; Rijke, Maarten D (2014), "Relative Upper Confidence Bound for the $K$-Armed Dueling Bandit Problem" (PDF), Proceedings of the 31st International Conference on Machine Learning (ICML-14), archived from the original (PDF) on 2016-03-26, retrieved 2016-04-27
- Gajane, Pratik; Urvoy, Tanguy; Clérot, Fabrice (2015), "A Relative Exponential Weighing Algorithm for Adversarial Utility-based Dueling Bandits" (PDF), Proceedings of the 32nd International Conference on Machine Learning (ICML-15), archived from the original (PDF) on 2015-09-08, retrieved 2016-04-29
- Zoghi, Masrour; Karnin, Zohar S; Whiteson, Shimon; Rijke, Maarten D (2015), "Copeland Dueling Bandits", Advances in Neural Information Processing Systems, NIPS'15, arXiv:1506.00312, Bibcode:2015arXiv150600312Z
- Komiyama, Junpei; Honda, Junya; Kashima, Hisashi; Nakagawa, Hiroshi (2015), "Regret Lower Bound and Optimal Algorithm in Dueling Bandit Problem" (PDF), Proceedings of the 28th Conference on Learning Theory, archived from the original (PDF) on 2016-06-17, retrieved 2016-04-27
- Wu, Huasen; Liu, Xin (2016), "Double Thompson Sampling for Dueling Bandits", The 30th Annual Conference on Neural Information Processing Systems (NIPS), arXiv:1604.07101, Bibcode:2016arXiv160407101W
- Cesa-Bianchi, Nicolo; Gentile, Claudio; Zappella, Giovanni (2013), A Gang of Bandits, Advances in Neural Information Processing Systems 26, NIPS 2013, arXiv:1306.0811
- Gentile, Claudio; Li, Shuai; Zappella, Giovanni (2014), "Online Clustering of Bandits", The 31st International Conference on Machine Learning, Journal of Machine Learning Research (ICML 2014), arXiv:1401.8257, Bibcode:2014arXiv1401.8257G
- Li, Shuai; Alexandros, Karatzoglou; Gentile, Claudio (2016), "Collaborative Filtering Bandits", The 39th International ACM SIGIR Conference on Information Retrieval (SIGIR 2016), arXiv:1502.03473, Bibcode:2015arXiv150203473L
- Gai, Y.; Krishnamachari, B.; Jain, R. (2010), "Learning multiuser channel allocations in cognitive radio networks: A combinatorial multi-armed bandit formulation", 2010 IEEE Symposium on New Frontiers in Dynamic Spectrum (PDF), pp. 1–9
- ^ Chen, Wei; Wang, Yajun; Yuan, Yang (2013), "Combinatorial multi-armed bandit: General framework and applications", Proceedings of the 30th International Conference on Machine Learning (ICML 2013) (PDF), pp. 151–159, archived from the original (PDF) on 2016-11-19, retrieved 2019-06-14
- ^ Santiago Ontañón (2017), "Combinatorial Multi-armed Bandits for Real-Time Strategy Games", Journal of Artificial Intelligence Research, 58: 665–702, arXiv:1710.04805, Bibcode:2017arXiv171004805O, doi:10.1613/jair.5398, S2CID 8517525
Further reading
- Guha, S.; Munagala, K.; Shi, P. (2010), "Approximation algorithms for restless bandit problems", Journal of the ACM, 58: 1–50, arXiv:0711.3861, doi:10.1145/1870103.1870106, S2CID 1654066
- Dayanik, S.; Powell, W.; Yamazaki, K. (2008), "Index policies for discounted bandit problems with availability constraints", Advances in Applied Probability, 40 (2): 377–400, doi:10.1239/aap/1214950209.
- Powell, Warren B. (2007), "Chapter 10", Approximate Dynamic Programming: Solving the Curses of Dimensionality, New York: John Wiley and Sons, ISBN 978-0-470-17155-4.
- Robbins, H. (1952), "Some aspects of the sequential design of experiments", Bulletin of the American Mathematical Society, 58 (5): 527–535, doi:10.1090/S0002-9904-1952-09620-8.
- Sutton, Richard; Barto, Andrew (1998), Reinforcement Learning, MIT Press, ISBN 978-0-262-19398-6, archived from the original on 2013-12-11.
- Allesiardo, Robin (2014), "A Neural Networks Committee for the Contextual Bandit Problem", Neural Information Processing – 21st International Conference, ICONIP 2014, Malaisia, November 03-06,2014, Proceedings, Lecture Notes in Computer Science, vol. 8834, Springer, pp. 374–381, arXiv:1409.8191, doi:10.1007/978-3-319-12637-1_47, ISBN 978-3-319-12636-4, S2CID 14155718.
- Weber, Richard (1992), "On the Gittins index for multiarmed bandits", Annals of Applied Probability, 2 (4): 1024–1033, doi:10.1214/aoap/1177005588, JSTOR 2959678.
- Katehakis, M.; C. Derman (1986), "Computing optimal sequential allocation rules in clinical trials", Adaptive statistical procedures and related topics, Institute of Mathematical Statistics Lecture Notes - Monograph Series, vol. 8, pp. 29–39, doi:10.1214/lnms/1215540286, ISBN 978-0-940600-09-6, JSTOR 4355518.
- Katehakis, Michael N.; Veinott, Jr., Arthur F. (1987), "The multi-armed bandit problem: decomposition and computation", Mathematics of Operations Research, 12 (2): 262–268, doi:10.1287/moor.12.2.262, JSTOR 3689689, S2CID 656323
External links
- MABWiser, open-source Python implementation of bandit strategies that supports context-free, parametric and non-parametric contextual policies with built-in parallelization and simulation capability.
- PyMaBandits, open-source implementation of bandit strategies in Python and Matlab.
- Contextual, open-source R package facilitating the simulation and evaluation of both context-free and contextual Multi-Armed Bandit policies.
- bandit.sourceforge.net Bandit project, open-source implementation of bandit strategies.
- Banditlib, open-source implementation of bandit strategies in C++.
- Leslie Pack Kaelbling and Michael L. Littman (1996). Exploitation versus Exploration: The Single-State Case.
- Tutorial: Introduction to Bandits: Algorithms and Theory. Part1. Part2.
- Feynman's restaurant problem, a classic example (with known answer) of the exploitation vs. exploration tradeoff.
- Bandit algorithms vs. A-B testing.
- S. Bubeck and N. Cesa-Bianchi A Survey on Bandits.
- A Survey on Contextual Multi-armed Bandits, a survey/tutorial for Contextual Bandits.
- Blog post on multi-armed bandit strategies, with Python code.
- Animated, interactive plots illustrating Epsilon-greedy, Thompson sampling, and Upper Confidence Bound exploration/exploitation balancing strategies.
| Differentiable computing | |
|---|---|
| General | |
| Hardware | |
| Software libraries | |
 , each distribution being associated with the rewards delivered by one of the
, each distribution being associated with the rewards delivered by one of the  levers. Let
levers. Let  be the mean values associated with these reward distributions. The gambler iteratively plays one lever per round and observes the associated reward. The objective is to maximize the sum of the collected rewards. The horizon
be the mean values associated with these reward distributions. The gambler iteratively plays one lever per round and observes the associated reward. The objective is to maximize the sum of the collected rewards. The horizon  is the number of rounds that remain to be played. The bandit problem is formally equivalent to a one-state
is the number of rounds that remain to be played. The bandit problem is formally equivalent to a one-state  after
after  rounds is defined as the expected difference between the reward sum associated with an optimal strategy and the sum of the collected rewards:
rounds is defined as the expected difference between the reward sum associated with an optimal strategy and the sum of the collected rewards:
 ,
,
 is the maximal reward mean,
is the maximal reward mean,  , and
, and  is the reward in round t.
is the reward in round t.
 tends to zero with probability 1 when the number of played rounds tends to infinity. Intuitively, zero-regret strategies are guaranteed to converge to a (not necessarily unique) optimal strategy if enough rounds are played.
tends to zero with probability 1 when the number of played rounds tends to infinity. Intuitively, zero-regret strategies are guaranteed to converge to a (not necessarily unique) optimal strategy if enough rounds are played.
 , and otherwise a reward of zero.
, and otherwise a reward of zero.
 is a sequence of actions at each time step
is a sequence of actions at each time step is a (random) stopping time which suggests when to stop collecting samples
is a (random) stopping time which suggests when to stop collecting samples is a guess on the best arm based on the data collected up to time
is a guess on the best arm based on the data collected up to time  , the objective is to identify the arm with the highest expected reward
, the objective is to identify the arm with the highest expected reward  minimizing probability of error
minimizing probability of error  .
.
 , the objective is to identify the arm with the highest expected reward
, the objective is to identify the arm with the highest expected reward  .
.
 where
where  is the machine no.1 (you can use a different variable respectively) and
is the machine no.1 (you can use a different variable respectively) and  is the amount for each time an attempt is made at pulling the lever, where
is the amount for each time an attempt is made at pulling the lever, where  , identify
, identify  as the sum of each attempts
as the sum of each attempts  , (...) as needed, and from there you can get a ratio, sum or mean as quantitative probability and sample your formulation for each slots.
, (...) as needed, and from there you can get a ratio, sum or mean as quantitative probability and sample your formulation for each slots.
 where
where  equal to each a unique machine slot,
equal to each a unique machine slot,  is the amount each time the lever is triggered,
is the amount each time the lever is triggered,  is the sum of
is the sum of  ,
,  would be the total available amount in your possession,
would be the total available amount in your possession,  reduced
reduced  as the sum of each gain or loss from
as the sum of each gain or loss from  (let's say you have 100$ that is defined as
(let's say you have 100$ that is defined as  and
and  would be a gain
would be a gain  is equal to a loss, from there you get your results either positive or negative to add for
is equal to a loss, from there you get your results either positive or negative to add for  as the maximum you are willing to spend.
It is possible to express this construction using a combination of multiple algebraic formulation, as mentioned above where you can limit with
as the maximum you are willing to spend.
It is possible to express this construction using a combination of multiple algebraic formulation, as mentioned above where you can limit with  of the trials, and a lever is selected at random (with uniform probability) for a proportion
of the trials, and a lever is selected at random (with uniform probability) for a proportion  . A typical parameter value might be
. A typical parameter value might be  , but this can vary widely depending on circumstances and predilections.
, but this can vary widely depending on circumstances and predilections. trials and the exploitation phase
trials and the exploitation phase  trials. During the exploration phase, a lever is randomly selected (with uniform probability); during the exploitation phase, the best lever is always selected.
trials. During the exploration phase, a lever is randomly selected (with uniform probability); during the exploitation phase, the best lever is always selected. regret is achievable. However, their work focuses on a finite set of policies, and the algorithm is computationally inefficient.
regret is achievable. However, their work focuses on a finite set of policies, and the algorithm is computationally inefficient.
![{\displaystyle \gamma \in (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dc19e2d373af486a2a9fe5dc8c3b749cf5756db) Initialisation:
Initialisation:  for
for  For each t = 1, 2, ..., T
1. Set
For each t = 1, 2, ..., T
1. Set 
 randomly according to the probabilities
randomly according to the probabilities  3. Receive reward
3. Receive reward  4. For
4. For  set:
set:


 it prefers arms with higher weights (exploit), it chooses with probability
it prefers arms with higher weights (exploit), it chooses with probability  to uniformly randomly explore. After receiving the rewards the weights are updated. The exponential growth significantly increases the weight of good arms.
to uniformly randomly explore. After receiving the rewards the weights are updated. The exponential growth significantly increases the weight of good arms.

 Initialisation:
Initialisation:  For each t = 1,2,...,T
1. For each arm generate a random noise from an exponential distribution
For each t = 1,2,...,T
1. For each arm generate a random noise from an exponential distribution  2. Pull arm
2. Pull arm  :
:  Add noise to each arm and pull the one with the highest value
3. Update value:
Add noise to each arm and pull the one with the highest value
3. Update value:  The rest remains the same
The rest remains the same
 . In the infinite armed case, introduced by Agrawal (1995), the "arms" are a continuous variable in
. In the infinite armed case, introduced by Agrawal (1995), the "arms" are a continuous variable in  :
:  . Thus,
. Thus,  no longer represents the whole sequence of expected (stationary) rewards for arm
no longer represents the whole sequence of expected (stationary) rewards for arm  denotes the sequence of expected rewards for arm
denotes the sequence of expected rewards for arm  .
.
 . Thus, the cumulative expected reward
. Thus, the cumulative expected reward  for the dynamic oracle at final time step
for the dynamic oracle at final time step 
 for policy
for policy  is computed as the difference between
is computed as the difference between 