Floyd's triangle is a triangular array of natural numbers used in computer science education. It is named after Robert Floyd. It is defined by filling the rows of the triangle with consecutive numbers, starting with a 1 in the top left corner:
| 1 | ||||
| 2 | 3 | |||
| 4 | 5 | 6 | ||
| 7 | 8 | 9 | 10 | |
| 11 | 12 | 13 | 14 | 15 |
The problem of writing a computer program to produce this triangle has been frequently used as an exercise or example for beginning computer programmers, covering the concepts of text formatting and simple loop constructs.
Properties
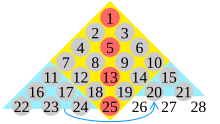
- The numbers along the left edge of the triangle are the lazy caterer's sequence and the numbers along the right edge are the triangular numbers. The nth row sums to n(n + 1)/2, the constant of an n × n magic square (sequence A006003 in the OEIS).
- Summing up the row sums in Floyd's triangle reveals the doubly triangular numbers, triangular numbers with an index that is triangular.
1 = 1 = T(T(1))
1 = 6 = T(T(2))
2 + 3
1
2 + 3 = 21 = T(T(3))
4 + 5 + 6
- Each number in the triangle is smaller than the number below it by the index of its row.
See also
References
- Keller, Arthur M. (1982), A first course in computer programming using PASCAL, McGraw-Hill, p. 39.
- Peters, James F. (1986), Pascal with program design, Holt, Rinehart and Winston, pp. 137, 154.
- Arora, Ashok; Bansal, Shefali (2005), Unix and C Programming, Firewall Media, p. 387, ISBN 9788170087618
- Xavier, C. (2007), C Language And Numerical Methods, New Age International, p. 155, ISBN 9788122411744
- Foster, Tony (2015), Doubly Triangular Numbers OEIS A002817.