Any vector space can be made into a unital associative algebra, called functional-theoretic algebra, by defining products in terms of two linear functionals. In general, it is a non-commutative algebra. It becomes commutative when the two functionals are the same.
Definition
Let AF be a vector space over a field F, and let L1 and L2 be two linear functionals on AF with the property L1(e) = L2(e) = 1F for some e in AF. We define multiplication of two elements x, y in AF by
It can be verified that the above multiplication is associative and that e is the identity of this multiplication.
So, AF forms an associative algebra with unit e and is called a functional theoretic algebra(FTA).
Suppose the two linear functionals L1 and L2 are the same, say L. Then AF becomes a commutative algebra with multiplication defined by
Example
X is a nonempty set and F a field. F is the set of functions from X to F.
If f, g are in F, x in X and α in F, then define
and
With addition and scalar multiplication defined as this, F is a vector space over F.
Now, fix two elements a, b in X and define a function e from X to F by e(x) = 1F for all x in X.
Define L1 and L2 from F to F by L1(f) = f(a) and L2(f) = f(b).
Then L1 and L2 are two linear functionals on F such that L1(e)= L2(e)= 1F For f, g in F define
Then F becomes a non-commutative function algebra with the function e as the identity of multiplication.
Note that
FTA of Curves in the Complex Plane
Let C denote the field of Complex numbers. A continuous function γ from the closed interval of real numbers to the field C is called a curve. The complex numbers γ(0) and γ(1) are, respectively, the initial and terminal points of the curve. If they coincide, the curve is called a loop. The set V of all the curves is a vector space over C.
We can make this vector space of curves into an algebra by defining multiplication as above. Choosing we have for α,β in C,
Then, V is a non-commutative algebra with e as the unity.
We illustrate this with an example.
Example of f-Product of Curves
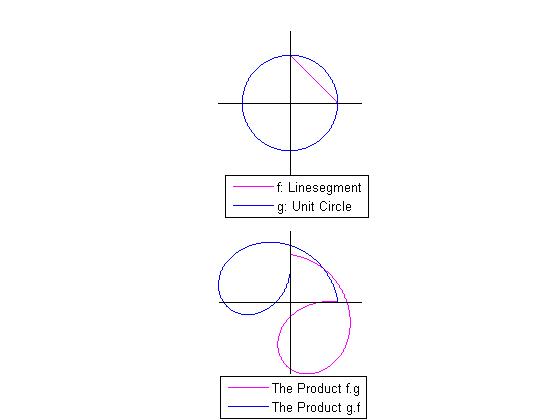
Let us take (1) the line segment joining the points (1, 0) and (0, 1) and (2) the unit circle with center at the origin. As curves in V, their equations can be obtained as
Since the circle g is a loop. The line segment f starts from : and ends at
Now, we get two f-products given by
and
Observe that showing that multiplication is non-commutative. Also both the products starts from
See also
References
- Sebastian Vattamattam and R. Sivaramakrishnan, A Note on Convolution Algebras, in Recent Trends in Mathematical Analysis, Allied Publishers, 2003.
- Sebastian Vattamattam and R. Sivaramakrishnan, Associative Algebras via Linear Functionals, Proceedings of the Annual Conference of K.M.A., Jan. 17 - 19, 2000, pp. 81-89
- Sebastian Vattamattam, Non-Commutative Function Algebras, in Bulletin of Kerala Mathematical Association, Vol. 4, No. 2, December 2007
- Sebastian Vattamattam, Transforming Curves by n-Curving, in Bulletin of Kerala Mathematics Association, Vol. 5, No. 1, December 2008
- Sebastian Vattamattam, Book of Beautiful Curves, January 2015
- R. Sivaramakrishnan, Certain Number Theoretic Episodes in Algebra, Chapman and Hall/CRC
Certain Number Theoretic Episodes in Algebra
Category:





 we have for α,β in C,
we have for α,β in C,


 the circle g
is a loop.
The line segment f starts from :
the circle g
is a loop.
The line segment f starts from : and ends at
and ends at 
 given by
given by


 showing that
multiplication is non-commutative. Also both the products starts from
showing that
multiplication is non-commutative. Also both the products starts from 