Page version status
This is an accepted version of this page
For broader coverage of this topic, see Spatial reference system.

| Geodesy | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||||||||||||||||||
| Fundamentals | ||||||||||||||||||||||||||
| Concepts | ||||||||||||||||||||||||||
| Technologies | ||||||||||||||||||||||||||
Standards (history)
|
||||||||||||||||||||||||||
A geographic coordinate system (GCS) is a spherical or geodetic coordinate system for measuring and communicating positions directly on Earth as latitude and longitude. It is the simplest, oldest and most widely used type of the various spatial reference systems that are in use, and forms the basis for most others. Although latitude and longitude form a coordinate tuple like a cartesian coordinate system, the geographic coordinate system is not cartesian because the measurements are angles and are not on a planar surface.
A full GCS specification, such as those listed in the EPSG and ISO 19111 standards, also includes a choice of geodetic datum (including an Earth ellipsoid), as different datums will yield different latitude and longitude values for the same location.
History
See also: History of geodesyThe invention of a geographic coordinate system is generally credited to Eratosthenes of Cyrene, who composed his now-lost Geography at the Library of Alexandria in the 3rd century BC. A century later, Hipparchus of Nicaea improved on this system by determining latitude from stellar measurements rather than solar altitude and determining longitude by timings of lunar eclipses, rather than dead reckoning. In the 1st or 2nd century, Marinus of Tyre compiled an extensive gazetteer and mathematically plotted world map using coordinates measured east from a prime meridian at the westernmost known land, designated the Fortunate Isles, off the coast of western Africa around the Canary or Cape Verde Islands, and measured north or south of the island of Rhodes off Asia Minor. Ptolemy credited him with the full adoption of longitude and latitude, rather than measuring latitude in terms of the length of the midsummer day.
Ptolemy's 2nd-century Geography used the same prime meridian but measured latitude from the Equator instead. After their work was translated into Arabic in the 9th century, Al-Khwārizmī's Book of the Description of the Earth corrected Marinus' and Ptolemy's errors regarding the length of the Mediterranean Sea, causing medieval Arabic cartography to use a prime meridian around 10° east of Ptolemy's line. Mathematical cartography resumed in Europe following Maximus Planudes' recovery of Ptolemy's text a little before 1300; the text was translated into Latin at Florence by Jacopo d'Angelo around 1407.
In 1884, the United States hosted the International Meridian Conference, attended by representatives from twenty-five nations. Twenty-two of them agreed to adopt the longitude of the Royal Observatory in Greenwich, England as the zero-reference line. The Dominican Republic voted against the motion, while France and Brazil abstained. France adopted Greenwich Mean Time in place of local determinations by the Paris Observatory in 1911.
Latitude and longitude
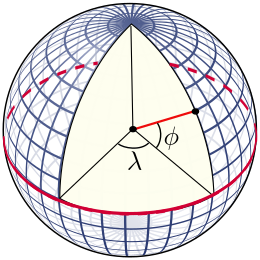
The latitude φ of a point on Earth's surface is the angle between the equatorial plane and the straight line that passes through that point and through (or close to) the center of the Earth. Lines joining points of the same latitude trace circles on the surface of Earth called parallels, as they are parallel to the Equator and to each other. The North Pole is 90° N; the South Pole is 90° S. The 0° parallel of latitude is designated the Equator, the fundamental plane of all geographic coordinate systems. The Equator divides the globe into Northern and Southern Hemispheres.
The longitude λ of a point on Earth's surface is the angle east or west of a reference meridian to another meridian that passes through that point. All meridians are halves of great ellipses (often called great circles), which converge at the North and South Poles. The meridian of the British Royal Observatory in Greenwich, in southeast London, England, is the international prime meridian, although some organizations—such as the French Institut national de l'information géographique et forestière—continue to use other meridians for internal purposes. The prime meridian determines the proper Eastern and Western Hemispheres, although maps often divide these hemispheres further west in order to keep the Old World on a single side. The antipodal meridian of Greenwich is both 180°W and 180°E. This is not to be conflated with the International Date Line, which diverges from it in several places for political and convenience reasons, including between far eastern Russia and the far western Aleutian Islands.
The combination of these two components specifies the position of any location on the surface of Earth, without consideration of altitude or depth. The visual grid on a map formed by lines of latitude and longitude is known as a graticule. The origin/zero point of this system is located in the Gulf of Guinea about 625 km (390 mi) south of Tema, Ghana, a location often facetiously called Null Island.
Geodetic datum
Main article: Geodetic datum Further information: Figure of the Earth, Reference ellipsoid, Geographic coordinate conversion, and Spatial reference systemIn order to use the theoretical definitions of latitude, longitude, and height to precisely measure actual locations on the physical earth, a geodetic datum must be used. A horizonal datum is used to precisely measure latitude and longitude, while a vertical datum is used to measure elevation or altitude. Both types of datum bind a mathematical model of the shape of the earth (usually a reference ellipsoid for a horizontal datum, and a more precise geoid for a vertical datum) to the earth. Traditionally, this binding was created by a network of control points, surveyed locations at which monuments are installed, and were only accurate for a region of the surface of the Earth. Newer datums are based on a global network for satellite measurements (GNSS, VLBI, SLR and DORIS).
This combination of mathematical model and physical binding mean that anyone using the same datum will obtain the same location measurement for the same physical location. However, two different datums will usually yield different location measurements for the same physical location, which may appear to differ by as much as several hundred meters; this not because the location has moved, but because the reference system used to measure it has shifted. Because any spatial reference system or map projection is ultimately calculated from latitude and longitude, it is crucial that they clearly state the datum on which they are based. For example, a UTM coordinate based on a WGS84 realisation will be different than a UTM coordinate based on NAD27 for the same location. Converting coordinates from one datum to another requires a datum transformation such as a Helmert transformation, although in certain situations a simple translation may be sufficient.
Datums may be global, meaning that they represent the whole Earth, or they may be regional, meaning that they represent an ellipsoid best-fit to only a portion of the Earth. Examples of global datums include the several realizations of WGS 84 (with the 2D datum ensemble EPSG:4326 with 2 meter accuracy as identifier) used for the Global Positioning System, and the several realizations of the International Terrestrial Reference System and Frame (such as ITRF2020 with subcentimeter accuracy), which takes into account continental drift and crustal deformation.
Datums with a regional fit of the ellipsoid that are chosen by a national cartographical organization include the North American Datums, the European ED50, and the British OSGB36. Given a location, the datum provides the latitude and longitude . In the United Kingdom there are three common latitude, longitude, and height systems in use. WGS 84 differs at Greenwich from the one used on published maps OSGB36 by approximately 112 m. ED50 differs from about 120 m to 180 m.
Points on the Earth's surface move relative to each other due to continental plate motion, subsidence, and diurnal Earth tidal movement caused by the Moon and the Sun. This daily movement can be as much as a meter. Continental movement can be up to 10 cm a year, or 10 m in a century. A weather system high-pressure area can cause a sinking of 5 mm. Scandinavia is rising by 1 cm a year as a result of the melting of the ice sheets of the last ice age, but neighboring Scotland is rising by only 0.2 cm. These changes are insignificant if a regional datum is used, but are statistically significant if a global datum is used.
Length of a degree
Main articles: Length of a degree of latitude and Length of a degree of longitude See also: Arc length § Great circles on EarthOn the GRS 80 or WGS 84 spheroid at sea level at the Equator, one latitudinal second measures 30.715 m, one latitudinal minute is 1843 m and one latitudinal degree is 110.6 km. The circles of longitude, meridians, meet at the geographical poles, with the west–east width of a second naturally decreasing as latitude increases. On the Equator at sea level, one longitudinal second measures 30.92 m, a longitudinal minute is 1855 m and a longitudinal degree is 111.3 km. At 30° a longitudinal second is 26.76 m, at Greenwich (51°28′38″N) 19.22 m, and at 60° it is 15.42 m.
On the WGS 84 spheroid, the length in meters of a degree of latitude at latitude ϕ (that is, the number of meters you would have to travel along a north–south line to move 1 degree in latitude, when at latitude ϕ), is about
The returned measure of meters per degree latitude varies continuously with latitude.
Similarly, the length in meters of a degree of longitude can be calculated as
(Those coefficients can be improved, but as they stand the distance they give is correct within a centimeter.)
The formulae both return units of meters per degree.
An alternative method to estimate the length of a longitudinal degree at latitude is to assume a spherical Earth (to get the width per minute and second, divide by 60 and 3600, respectively):
where Earth's average meridional radius is 6,367,449 m. Since the Earth is an oblate spheroid, not spherical, that result can be off by several tenths of a percent; a better approximation of a longitudinal degree at latitude is
where Earth's equatorial radius equals 6,378,137 m and ; for the GRS 80 and WGS 84 spheroids, . ( is known as the reduced (or parametric) latitude). Aside from rounding, this is the exact distance along a parallel of latitude; getting the distance along the shortest route will be more work, but those two distances are always within 0.6 m of each other if the two points are one degree of longitude apart.
| Latitude | City | Degree | Minute | Second | 0.0001° |
|---|---|---|---|---|---|
| 60° | Saint Petersburg | 55.80 km | 0.930 km | 15.50 m | 5.58 m |
| 51° 28′ 38″ N | Greenwich | 69.47 km | 1.158 km | 19.30 m | 6.95 m |
| 45° | Bordeaux | 78.85 km | 1.31 km | 21.90 m | 7.89 m |
| 30° | New Orleans | 96.49 km | 1.61 km | 26.80 m | 9.65 m |
| 0° | Quito | 111.3 km | 1.855 km | 30.92 m | 11.13 m |
Alternate encodings
Like any series of multiple-digit numbers, latitude-longitude pairs can be challenging to communicate and remember. Therefore, alternative schemes have been developed for encoding GCS coordinates into alphanumeric strings or words:
- the Maidenhead Locator System, popular with radio operators.
- the World Geographic Reference System (GEOREF), developed for global military operations, replaced by the current Global Area Reference System (GARS).
- Open Location Code or "Plus Codes", developed by Google and released into the public domain.
- Geohash, a public domain system based on the Morton Z-order curve.
- Mapcode, an open-source system originally developed at TomTom.
- What3words, a proprietary system that encodes GCS coordinates as pseudorandom sets of words by dividing the coordinates into three numbers and looking up words in an indexed dictionary.
These are not distinct coordinate systems, only alternative methods for expressing latitude and longitude measurements.
See also
- Decimal degrees – Angular measurements, typically for latitude and longitude
- Geographical distance – Distance measured along the surface of the Earth
- Geographic information system – System to capture, manage, and present geographic data
- Geo URI scheme – System of geographic location identifiers
- ISO 6709, standard representation of geographic point location by coordinates
- Linear referencing – method of spatial referencingPages displaying wikidata descriptions as a fallback
- Primary direction – Celestial coordinate system used to specify the positions of celestial objectsPages displaying short descriptions of redirect targets
- Planetary coordinate system
- Spatial reference system – System to specify locations on Earth
- Jan Smits (2015). Mathematical data for bibliographic descriptions of cartographic materials and spatial data. Geographical co-ordinates. ICA Commission on Map Projections.
Notes
- The pair had accurate absolute distances within the Mediterranean but underestimated the circumference of the Earth, causing their degree measurements to overstate its length west from Rhodes or Alexandria, respectively.
- Alternative versions of latitude and longitude include geocentric coordinates, which measure with respect to Earth's center; geodetic coordinates, which model Earth as an ellipsoid; and geographic coordinates, which measure with respect to a plumb line at the location for which coordinates are given.
- WGS 84 is the default datum used in most GPS equipment, but other datums and map projections can be selected.
References
- Chang, Kang-tsung (2016). Introduction to Geographic Information Systems (9th ed.). McGraw-Hill. p. 24. ISBN 978-1-259-92964-9.
- DiBiase, David. "The Nature of Geographic Information". Archived from the original on 19 February 2024. Retrieved 18 February 2024.
- "Using the EPSG geodetic parameter dataset, Guidance Note 7-1". EPSG Geodetic Parameter Dataset. Geomatic Solutions. Archived from the original on 15 December 2021. Retrieved 15 December 2021.
- McPhail, Cameron (2011), Reconstructing Eratosthenes' Map of the World (PDF), Dunedin: University of Otago, pp. 20–24, archived (PDF) from the original on 2 April 2015, retrieved 14 March 2015.
- Evans, James (1998), The History and Practice of Ancient Astronomy, Oxford, England: Oxford University Press, pp. 102–103, ISBN 9780199874453, archived from the original on 17 March 2023, retrieved 5 May 2020.
- "The International Meridian Conference". Millennium Dome: The O2 in Greenwich. Greenwich 2000 Limited. 9 June 2011. Archived from the original on 6 August 2012. Retrieved 31 October 2012.
- American Society of Civil Engineers (1 January 1994). Glossary of the Mapping Sciences. ASCE Publications. p. 224. ISBN 9780784475706.
- "Making maps compatible with GPS". Government of Ireland 1999. Archived from the original on 21 July 2011. Retrieved 15 April 2008.
- "A guide to the coordinate systems in Great Britain". Ordnance Survey.
- "WGS 84: EPSG Projection -- Spatial Reference". spatialreference.org. Archived from the original on 13 May 2020. Retrieved 5 May 2020.
- EPSG:4326
- Bolstad, Paul (2012). GIS Fundamentals (PDF) (5th ed.). Atlas books. p. 102. ISBN 978-0-9717647-3-6. Archived from the original (PDF) on 15 October 2020. Retrieved 27 January 2018.
- ^ A guide to coordinate systems in Great Britain (PDF), D00659 v3.6, Ordnance Survey, 2020, archived (PDF) from the original on 2 April 2020, retrieved 17 December 2021
- ^ Archived 29 June 2016 at the Wayback Machine Geographic Information Systems – Stackexchange
Sources
- Portions of this article are from Jason Harris' "Astroinfo" which is distributed with KStars, a desktop planetarium for Linux/KDE. See The KDE Education Project – KStars Archived 17 May 2008 at the Wayback Machine
External links
 Media related to Geographic coordinate system at Wikimedia Commons
Media related to Geographic coordinate system at Wikimedia Commons
 and longitude
and longitude  . In the United Kingdom there are three common latitude, longitude, and height systems in use. WGS 84 differs at Greenwich from the one used on published maps OSGB36 by approximately 112 m. ED50 differs from about 120 m to 180 m.
. In the United Kingdom there are three common latitude, longitude, and height systems in use. WGS 84 differs at Greenwich from the one used on published maps OSGB36 by approximately 112 m. ED50 differs from about 120 m to 180 m.



 is 6,367,449 m. Since the Earth is an
is 6,367,449 m. Since the Earth is an 
 equals 6,378,137 m and
equals 6,378,137 m and  ; for the GRS 80 and WGS 84 spheroids,
; for the GRS 80 and WGS 84 spheroids,  . (
. ( is known as the
is known as the 