
 Two shot groupings obtained with different firearms at different distances.
Two shot groupings obtained with different firearms at different distances. The group on the left measures about 13 mm and was fired at about 45 meters, which equals 13 mm/45 m = 0.29 mils (1⁄2 in group at 50 yards, approx. 1.047′×50/100 = 0.524′).
The group on the right measures about 7 mm and was fired at about 90 meters, which equals 7 mm/90 m = 0.08 mils (0.3 in group at 100 yards, approx. 1.047′×0.3 = 0.314′).
In shooting sports, a shot grouping, or simply group, is the collective pattern of projectile impacts on a target from multiple consecutive shots taken in one shooting session. The tightness of the grouping (the proximity of all the shots to each other) is a measure of the precision of a weapon, and a measure of the shooter's consistency and skill. On the other hand, the grouping displacement (the distance between the calculated group center and the intended point of aim) is a measure of accuracy.
Tightness of shot groupings are calculated by measuring the maximum distance between any two bullet holes on the target (center-to-center) in length measurements such as millimeters or inches. Often that measurement is converted into angular measurements such as milliradians ("mils" or "mrads") or minutes of angle (MOAs), which expresses the size of shot scatter regardless of the target distance. Thus, by using angular measurements, one can reliably compare the relative tightness of shot groupings fired at different distances.
Uses of the term
For firearms that shoot one round at a time, a shot grouping test can be used to measure the accuracy of the entire shooting system: the weapon's mechanical precision and the uniformity of the ammunition. The weapon is fixed into position on a test mount, and aimed at a target. Multiple shots using rounds from the same type and batch are fired to observe how the weapon groups the shots. If a person holds the weapon and shoots it, the grouping measures the combination of the person's skill and the weapon's accuracy.
In shotgun shooting, the grouping is also called the pattern or "spread". The pattern indicates the extent of scattering by shots from a single shotshell, measured as the smallest circle containing all the shots on the target. The barrel of a shotgun is choked to deliver a wider or narrower scattering, depending on the expected use. Shooting at close range indicates a cylinder bore barrel to deliver a wide grouping, while for hunting at longer distances such as 50 yards or meters, a choke is recommended to constrict the scattering for a tighter pattern.
In archery, a shot grouping is the result of one person shooting multiple arrows at a target. A tight grouping indicates consistency in the archer's form.
Firearms
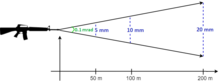
Mean point of impact (MPI) is the calculated center of the grouping, which is the average center of all the shots, and is not necessarily located at a hole in the target. The process of mechanically readjusting the gunsight's point of aim to match the MPI is called sighting in or "zeroing" the gun. The size of the grouping is described as the diameter of the smallest circle that can be drawn to contain all the shots, typically only measured from the center points of each impact (known as "center-to-center size").
A "flier" is a shot from the same shooting session that is distinctly farther from the general grouping, considered to be the outlier of the group. Such shots may be the result of trajectory deviation caused by unexpected changes in wind condition (known as a "wind shift" or "gust"), a muscular flinch of the shooter at the time of the trigger pull, a problem with the firearm mechanism, poor tuning of barrel harmonics, or inconsistency in the ammunition (e.g. bullet/pellet weight and aerodynamics, propellant load and efficiency, muzzle velocity). Infrequent single fliers may be discounted when evaluating large cohorts, but if random fliers occur often, then the problem is considered significant and should be traced to its origin.
While target shooting with a handgun, if a grouping is consistently off-center then the shooter is instructed to alter the body angle or the stance, rather than shifting the arm, wrist or hand, which should remain in position.
Metric units
When using the SI or metric units, shooting accuracy is more easily measured in milliradians ("mil" or "mrad" for short), which is an arc-based angular unit corresponding to 1/1,000th of a radian, and mathematically a direct ratio between the length of a circular arc and its radius. When imagining the shooter as the center of a two-dimensional circle, and his lines of sight as rays projecting from that center, the group size can be geometrically considered a very short length of arc, and the distance to the target as the radius.
By measuring the group size in millimeters (or in centimeters and then multiplying by a conversion factor of 10) and the distance to target in meters, the numerical conversion between radians and milliradians is cancelled out, and the angular measurement can be very easily calculated as a simple division:
And conversely, the group size of 1 milliradian at 100 meters (the default metric sighting-in distance) can be determined just as easily:
Since shot grouping are very small angles, the linear formula above can be used as an extremely good approximation for group sizes in milliradians. The error of assuming that 0.1 mil (the typical click value on mil-based adjustment wheels) equals "10 mm (1 cm) at 100 meters" is about 1×10% (or 0.0000001%).
Metric units can also be used to calculate group sizes in minutes of arc, though this is mathematically inconvenient due to the need to convert between central angle and arc length, which involves multiplication with the irrational mathematical constant π:
In the above formula, "1000" is the conversion factor between meters and millimeters; "10800" is how many arcminutes are within a 180-degree semicircle, whose arc length is "π × r" and "r" corresponds to the distance in meters.
And conversely:
Therefore, at 100 m, a 1 MOA group can be represented approximately by a 29 mm circle, slightly smaller than a half dollar coin.
Imperial units
When using imperial units, shooting accuracy is more easily measured in minutes of arc or arcminutes (symbol ′, also called "minutes of angle", or "MOA" for short), which is an angular unit equal to 1/60th of a degree. A full 360-degree circle surrounding a shooter therefore always has 360 × 60 = 21,600 arcminutes, and a semi-circle always has 10,800 arcminutes.
By measuring the grouping size as a short arc (measured in inches) on a circle whose radius corresponds to the distance to target (measured in yards), the angular measurement can be calculated using simple geometry:
In the above formula, "36" is the conversion factor between yards and inches.
Conversely, the group size of 1 arcminute at 100 yards (the most commonly used sighting-in distance in North America) can also be calculated:
The linear formula above for measuring group sizes using arcminutes with imperial units is less precise than using milliradians with metric units, but can still be a good approximation depending on the demands for precision. When shooting at a target 100 yards away, a 1 MOA group is a circle of approximately 1.047 inch diameter, roughly the size of a dollar coin. This coincidentally can be rounded down to just 1 inch, and the round-off error of assuming 1 MOA equals "1 inch at 100 yards" is about 4.5%, which is considered acceptable in most shooting applications.
Benchmarks
A big-game hunting rifle is considered accurate if its shots fall within 1.5 MOA (≈ 0.5 mil), while a rifle intended for small animals is expected to have an accuracy of 1 MOA or less (under 0.3 mil, also known as "sub-MOA"). Handguns are typically less accurate; at a shooting distance of 25 yd, a grouping is considered acceptable for self-defense if the shots fall within a circle of 4 to 5 inches, which is 15 to 19 MOA (equivalent to a grouping of 100-150 mm at 25 meters, which is 4-6 mils), representing the shot pattern needed to hit the vital organs of a human target. Expensive and well-machined match-grade pistols demonstrate a higher accuracy than normal handguns, capable of groupings of 1.25 inches at 25 yards, which is about 5 MOA (equivalent to about 30 mm at 25 meters, which is 1.2 mil).
Archery
With the increased element of human skill in archery, a grouping on target is more a measure of the archer's skill. If an archer is not getting a consistent grouping, then their basic form needs work. If an archer's arrows are grouping on target but off center, this shows consistent basic form, with better results achievable after slight adjustments.
On the equipment side, bow stabilizers have been used since the 1960s by tournament competitors and by bow hunters to counteract the torque of shooting the arrow. A tighter grouping may be achieved with such a stabilizer, which adds mass extending outward on a moment arm, usually mounted perpendicular to the bow riser, aligned with the arrow path.
Example groupings
-
 Handgun and paper target showing grouping of ten shots
Handgun and paper target showing grouping of ten shots
-
 A grouping made with a five-shot revolver
A grouping made with a five-shot revolver
-
 Eight-shot grouping
Eight-shot grouping
-
 Multiple shots from a semi-automatic handgun
Multiple shots from a semi-automatic handgun
-
 Arrow grouping with fairly consistent results but slightly off center
Arrow grouping with fairly consistent results but slightly off center
-
 Long Range Sniper Rifle Grouping
Long Range Sniper Rifle Grouping
References
- ^ Matunas, Edward (2003). Do-it-yourself Gun Repair: Gunsmithing at Home. Woods N' Water. pp. 65–6. ISBN 978-0-9722804-2-6.
- ^ Watson, David (2014). ABCs of Rifle Shooting. F+W Media. pp. 196–8. ISBN 978-1-4402-3897-0.
- Moller, Cliff. "Understanding Shotgun Chokes, A brief explanation by Briley". Briley Manufacturing. Archived from the original on July 29, 2015. Retrieved August 10, 2015.
- ^ Engh, Douglas (2005). Archery Fundamentals. Human Kinetics. pp. 72–3, 86. ISBN 978-0-7360-5501-7.
- Gilbert, Randall (2003). A to Z Guide to White-tailed Deer and Deer Hunting. Woods N' Water. p. 87. ISBN 978-0-9707493-9-0.
- McDougall, Len (2013). The Self-Reliance Manifesto: Essential Outdoor Survival Skills. Skyhorse. pp. 172–75. ISBN 9781628733006.
- McGivern, Ed (2007). Ed McGivern's Book of Fast and Fancy Revolver Shooting. Skyhorse Publishing. p. 214. ISBN 978-1-60239-086-7.
- Dexadine Ballistics Software - ballistic data for shooting and reloading
- Campbell, Robert K. (2009). The Gun Digest Book of Personal Protection & Home Defense. Krause Publications. p. 31. ISBN 978-0-89689-938-4.
- Shideler, Dan; Sigler, Derrek; Ramage, Ken (2008). The Gun Digest Book of Tactical Gear. Gun Digest Books. p. 87. ISBN 978-0-89689-684-0.
- Haywood, Kathleen; Lewis, Catherine (2013). Archery: Steps to Success (4 ed.). Human Kinetics. p. 42. ISBN 978-1-4504-4468-2.
- Bertalan, Dan (2013). The Traditional Bowyers Encyclopedia. Skyhorse Publishing. p. 293. ISBN 978-1-62873-012-8.
- Haywood and Lewis 2013, p. 15.
- Ruis, Steve; Stevenson, Claudia (2004). Precision Archery. Human Kinetics. p. 131. ISBN 978-0-7360-4634-3.





