Heisenberg's microscope is a thought experiment proposed by Werner Heisenberg that has served as the nucleus of some commonly held ideas about quantum mechanics. In particular, it provides an argument for the uncertainty principle on the basis of the principles of classical optics.
The concept was criticized by Heisenberg's mentor Niels Bohr, and theoretical and experimental developments have suggested that Heisenberg's intuitive explanation of his mathematical result might be misleading. While the act of measurement does lead to uncertainty, the loss of precision is less than that predicted by Heisenberg's argument when measured at the level of an individual state. The formal mathematical result remains valid, however, and the original intuitive argument has also been vindicated mathematically when the notion of disturbance is expanded to be independent of any specific state.
Heisenberg's argument
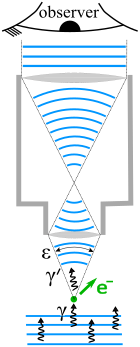
Heisenberg supposes that an electron is like a classical particle, moving in the direction along a line below the microscope. Let the cone of light rays leaving the microscope lens and focusing on the electron make an angle with the electron. Let be the wavelength of the light rays. Then, according to the laws of classical optics, the microscope can only resolve the position of the electron up to an accuracy of
An observer perceives an image of the particle because the light rays strike the particle and bounce back through the microscope to the observer's eye. We know from experimental evidence that when a photon strikes an electron, the latter has a Compton recoil with momentum proportional to , where is the Planck constant. However, the extent of "recoil cannot be exactly known, since the direction of the scattered photon is undetermined within the bundle of rays entering the microscope." In particular, the electron's momentum in the direction is only determined up to
Combining the relations for and , we thus have
- ,
which is an approximate expression of Heisenberg's uncertainty principle.
Analysis of argument
Although the thought experiment was formulated as an introduction to Heisenberg's uncertainty principle, one of the pillars of modern physics, it attacks the very premises under which it was constructed, thereby contributing to the development of an area of physics—namely, quantum mechanics—that redefined the terms under which the original thought experiment was conceived.
Some interpretations of quantum mechanics question whether an electron actually has a determinate position before it is disturbed by the measurement used to establish said determinate position. Under the Copenhagen interpretation, an electron has some probability of showing up at any point in the universe, though the probability that it will be far from where one expects becomes very low at great distances from the neighborhood in which it is originally found. In other words, the "position" of an electron can only be stated in terms of a probability distribution, as can predictions of where it may move.
See also
- Atom localization
- Quantum mechanics
- Basics of quantum mechanics
- Interpretation of quantum mechanics
- Philosophical interpretation of classical physics
- Schrödinger's cat
- Uncertainty principle
- Quantum field theory
- Electromagnetic radiation
References
- Lee A. Rozema; et al. (6 Sep 2012). "Violation of Heisenberg's Measurement–Disturbance Relationship by Weak Measurements". Phys. Rev. Lett. 109 (18): 100404. arXiv:1208.0034. Bibcode:2012PhRvL.109j0404R. doi:10.1103/PhysRevLett.109.100404. PMID 23005268. S2CID 37576344.
- "Scientists cast doubt on Heisenberg's uncertainty principle". Science Daily. 7 Sep 2012.
- Paul Busch; Pekka Lahti; Richard Werner (Oct 2013). "Proof of Heisenberg's error–disturbance relation". Physical Review Letters. 111 (16): 160405. arXiv:1306.1565. Bibcode:2013PhRvL.111p0405B. doi:10.1103/PhysRevLett.111.160405. PMID 24182239. S2CID 24507489.
- Lett, Caron (17 Oct 2013). "Scientists prove Heisenberg's intuition correct". University of York.
- Werner Heisenberg (1949). The Physical Principles of the Quantum Theory. Courier Dover Publications. ISBN 978-0-486-60113-7.
- ^ Richmond, Michael. "Heisenberg's Microscope". Retrieved 1 Sep 2016.
Sources
- Aczel, Amir (2003). Entanglement : the unlikely story of how scientists, mathematicians, and philosophers proved Einstein's spookiest theory. New York: Plume. p. 77–79. ISBN 978-0-452-28457-9. OCLC 53378914.
- Bohr, N. (1928). "The Quantum Postulate and the Recent Development of Atomic Theory". Nature. 121 (3050). Springer Science and Business Media LLC: 580–590. Bibcode:1928Natur.121..580B. doi:10.1038/121580a0. ISSN 0028-0836. S2CID 4097746.
- Heisenberg, Werner (2007). Physics & philosophy : the revolution in modern science. New York: HarperPerennial. p. 46. ISBN 978-0-06-120919-2. OCLC 135128032.
- Messiah, Albert (2014). Quantum Mechanics. Vol. I. Dover Publications. p. 143. ISBN 978-0-486-78455-7. OCLC 874097814.
- Newman, James (2003). The World of Mathematics Set. Vol. II. City: Dover Publications. p. 1051–1055. ISBN 978-0-486-43268-7. OCLC 691512261.
External links
- History of Heisenberg's Microscope Archived 2005-12-02 at the Wayback Machine
- Lectures on Heisenberg's Microscope
 direction along a line below the microscope. Let the
direction along a line below the microscope. Let the  with the electron. Let
with the electron. Let  be the
be the 
 , where
, where  is the
is the 
 and
and  , we thus have
, we thus have
 ,
,