Misplaced Pages

Hyperrectangle Orthotope
A rectangular cuboid is a 3-orthotope
Type	Prism
Faces	2n
Edges	n × 2
Vertices	2
Schläfli symbol	{}×{}×···×{} = {}
Coxeter diagram	···
Symmetry group	, order 2
Dual polyhedron	Rectangular n-fusil
Properties	convex, zonohedron, isogonal

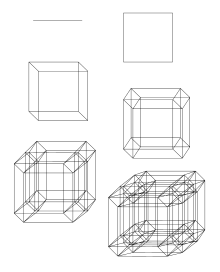
In geometry, a hyperrectangle (also called a box, hyperbox, ${\displaystyle k}$-cell or orthotope), is the generalization of a rectangle (a plane figure) and the rectangular cuboid (a solid figure) to higher dimensions. A necessary and sufficient condition is that it is congruent to the Cartesian product of finite intervals. This means that a ${\displaystyle k}$-dimensional rectangular solid has each of its edges equal to one of the closed intervals used in the definition. Every ${\displaystyle k}$-cell is compact.

If all of the edges are equal length, it is a hypercube. A hyperrectangle is a special case of a parallelotope.

Formal definition

For every integer ${\displaystyle i}$ from ${\displaystyle 1}$ to ${\displaystyle k}$, let ${\displaystyle a_{i}}$ and ${\displaystyle b_{i}}$ be real numbers such that ${\displaystyle a_{i}<b_{i}}$. The set of all points ${\displaystyle x=(x_{1},\dots ,x_{k})}$ in ${\displaystyle \mathbb {R} ^{k}}$ whose coordinates satisfy the inequalities ${\displaystyle a_{i}\leq x_{i}\leq b_{i}}$ is a ${\displaystyle k}$-cell.

Intuition

A ${\displaystyle k}$-cell of dimension ${\displaystyle k\leq 3}$ is especially simple. For example, a 1-cell is simply the interval ${\displaystyle }$ with ${\displaystyle a<b}$. A 2-cell is the rectangle formed by the Cartesian product of two closed intervals, and a 3-cell is a rectangular solid.

The sides and edges of a ${\displaystyle k}$-cell need not be equal in (Euclidean) length; although the unit cube (which has boundaries of equal Euclidean length) is a 3-cell, the set of all 3-cells with equal-length edges is a strict subset of the set of all 3-cells.

Types

A four-dimensional orthotope is likely a hypercuboid.

The special case of an n-dimensional orthotope where all edges have equal length is the n-cube or hypercube.

By analogy, the term "hyperrectangle" can refer to Cartesian products of orthogonal intervals of other kinds, such as ranges of keys in database theory or ranges of integers, rather than real numbers.

Dual polytope

n-fusil
Example: 3-fusil
Type	Prism
Faces	2n
Vertices	2
Schläfli symbol	{}+{}+···+{} = n{}
Coxeter diagram	...
Symmetry group	, order 2
Dual polyhedron	n-orthotope
Properties	convex, isotopal

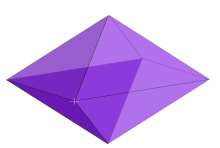
The dual polytope of an n-orthotope has been variously called a rectangular n-orthoplex, rhombic n-fusil, or n-lozenge. It is constructed by 2n points located in the center of the orthotope rectangular faces.

An n-fusil's Schläfli symbol can be represented by a sum of n orthogonal line segments: { } + { } + ... + { } or n{ }.

A 1-fusil is a line segment. A 2-fusil is a rhombus. Its plane cross selections in all pairs of axes are rhombi.

n	Example image
1	Line segment { }
2	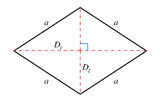Rhombus { } + { } = 2{ }
3	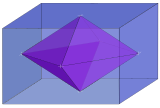Rhombic 3-orthoplex inside 3-orthotope { } + { } + { } = 3{ }

See also

• Minimum bounding rectangle
• Cuboid
• Hilbert cube

Notes

1. ^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.5 Spherical Coxeter groups, p.251
2. ^ Coxeter, 1973
3. Foran (1991)
4. Rudin (1976:39)
5. Foran (1991:24)
6. Rudin (1976:31)
7. Hirotsu, Takashi (2022). "Normal-sized hypercuboids in a given hypercube". arXiv:2211.15342.
8. See e.g. Zhang, Yi; Munagala, Kamesh; Yang, Jun (2011), "Storing matrices on disk: Theory and practice revisited" (PDF), Proc. VLDB, 4 (11): 1075–1086, doi:10.14778/3402707.3402743.

References

• Coxeter, Harold Scott MacDonald (1973). Regular Polytopes (3rd ed.). New York: Dover. pp. 122–123. ISBN 0-486-61480-8.

External links

• Weisstein, Eric W. "Orthotope". MathWorld.
• Foran, James (1991-01-07). Fundamentals of Real Analysis. CRC Press. ISBN 9780824784539. Retrieved 23 May 2014.
• Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill.

v t e Dimension
Dimensional spaces	Vector space Euclidean space Affine space Projective space Free module Manifold Algebraic variety Spacetime
Other dimensions	Krull Lebesgue covering Inductive Hausdorff Minkowski Fractal Degrees of freedom
Polytopes and shapes	Hyperplane Hypersurface Hypercube Hyperrectangle Demihypercube Hypersphere Cross-polytope Simplex Hyperpyramid
Number systems	Hypercomplex numbers Cayley–Dickson construction
Dimensions by number	Zero One Two Three Four Five Six Seven Eight n-dimensions
See also	Hyperspace Codimension
Category

• Polytopes
• Prismatoid polyhedra
• Multi-dimensional geometry