(Redirected from Lah numbers )
Mathematical sequence
Illustration of the unsigned Lah numbers for n and k between 1 and 4 In mathematics , the (signed and unsigned) Lah numbers are coefficients expressing rising factorials in terms of falling factorials and vice versa. They were discovered by Ivo Lah in 1954. Explicitly, the unsigned Lah numbers
L
(
n
,
k
)
{\displaystyle L(n,k)}
binomial coefficient
L
(
n
,
k
)
=
(
n
−
1
k
−
1
)
n
!
k
!
{\displaystyle L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}}
for
n
≥
k
≥
1
{\displaystyle n\geq k\geq 1}
Unsigned Lah numbers have an interesting meaning in combinatorics : they count the number of ways a set of
n
{\textstyle n}
partitioned into
k
{\textstyle k}
subsets . Lah numbers are related to Stirling numbers .
For
n
≥
1
{\textstyle n\geq 1}
L
(
n
,
1
)
{\textstyle L(n,1)}
factorial
n
!
{\textstyle n!}
{
1
,
2
,
3
}
{\textstyle \{1,2,3\}}
{
(
1
,
2
,
3
)
}
,
{
(
1
,
3
,
2
)
}
,
{
(
2
,
1
,
3
)
}
,
{
(
2
,
3
,
1
)
}
,
{
(
3
,
1
,
2
)
}
,
{
(
3
,
2
,
1
)
}
{\displaystyle \{(1,2,3)\},\{(1,3,2)\},\{(2,1,3)\},\{(2,3,1)\},\{(3,1,2)\},\{(3,2,1)\}}
L
(
3
,
2
)
{\textstyle L(3,2)}
{
1
,
2
,
3
}
{\textstyle \{1,2,3\}}
{
1
,
(
2
,
3
)
}
,
{
1
,
(
3
,
2
)
}
,
{
2
,
(
1
,
3
)
}
,
{
2
,
(
3
,
1
)
}
,
{
3
,
(
1
,
2
)
}
,
{
3
,
(
2
,
1
)
}
{\displaystyle \{1,(2,3)\},\{1,(3,2)\},\{2,(1,3)\},\{2,(3,1)\},\{3,(1,2)\},\{3,(2,1)\}}
L
(
n
,
n
)
{\textstyle L(n,n)}
{
1
,
2
,
…
,
n
}
{\textstyle \{1,2,\ldots ,n\}}
n
{\displaystyle n}
Karamata –Knuth style notation has taken over. Lah numbers are now often written as
L
(
n
,
k
)
=
⌊
n
k
⌋
{\displaystyle L(n,k)=\left\lfloor {n \atop k}\right\rfloor }
Table of values
Below is a table of values for the Lah numbers:
kn
0
1
2
3
4
5
6
7
8
9
10
0
1
1
0
1
2
0
2
1
3
0
6
6
1
4
0
24
36
12
1
5
0
120
240
120
20
1
6
0
720
1800
1200
300
30
1
7
0
5040
15120
12600
4200
630
42
1
8
0
40320
141120
141120
58800
11760
1176
56
1
9
0
362880
1451520
1693440
846720
211680
28224
2016
72
1
10
0
3628800
16329600
21772800
12700800
3810240
635040
60480
3240
90
1
The row sums are
1
,
1
,
3
,
13
,
73
,
501
,
4051
,
37633
,
…
{\textstyle 1,1,3,13,73,501,4051,37633,\dots }
A000262 in the OEIS ).
Rising and falling factorials
Let
x
(
n
)
{\textstyle x^{(n)}}
rising factorial
x
(
x
+
1
)
(
x
+
2
)
⋯
(
x
+
n
−
1
)
{\textstyle x(x+1)(x+2)\cdots (x+n-1)}
(
x
)
n
{\textstyle (x)_{n}}
falling factorial
x
(
x
−
1
)
(
x
−
2
)
⋯
(
x
−
n
+
1
)
{\textstyle x(x-1)(x-2)\cdots (x-n+1)}
x
(
n
)
=
∑
k
=
0
n
L
(
n
,
k
)
(
x
)
k
{\displaystyle x^{(n)}=\sum _{k=0}^{n}L(n,k)(x)_{k}}
(
x
)
n
=
∑
k
=
0
n
(
−
1
)
n
−
k
L
(
n
,
k
)
x
(
k
)
.
{\displaystyle (x)_{n}=\sum _{k=0}^{n}(-1)^{n-k}L(n,k)x^{(k)}.}
x
(
x
+
1
)
(
x
+
2
)
=
6
x
+
6
x
(
x
−
1
)
+
1
x
(
x
−
1
)
(
x
−
2
)
{\displaystyle x(x+1)(x+2)={\color {red}6}x+{\color {red}6}x(x-1)+{\color {red}1}x(x-1)(x-2)}
x
(
x
−
1
)
(
x
−
2
)
=
6
x
−
6
x
(
x
+
1
)
+
1
x
(
x
+
1
)
(
x
+
2
)
,
{\displaystyle x(x-1)(x-2)={\color {red}6}x-{\color {red}6}x(x+1)+{\color {red}1}x(x+1)(x+2),}
where the coefficients 6, 6, and 1 are exactly the Lah numbers
L
(
3
,
1
)
{\displaystyle L(3,1)}
L
(
3
,
2
)
{\displaystyle L(3,2)}
L
(
3
,
3
)
{\displaystyle L(3,3)}
Identities and relations
The Lah numbers satisfy a variety of identities and relations.
In Karamata –Knuth notation for Stirling numbers
L
(
n
,
k
)
=
∑
j
=
k
n
[
n
j
]
{
j
k
}
{\displaystyle L(n,k)=\sum _{j=k}^{n}\left\left\{{j \atop k}\right\}}
[
n
j
]
{\textstyle \left}
unsigned Stirling numbers of the first kind and
{
j
k
}
{\textstyle \left\{{j \atop k}\right\}}
Stirling numbers of the second kind .
L
(
n
,
k
)
=
(
n
−
1
k
−
1
)
n
!
k
!
=
(
n
k
)
(
n
−
1
)
!
(
k
−
1
)
!
=
(
n
k
)
(
n
−
1
k
−
1
)
(
n
−
k
)
!
{\displaystyle L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}={n \choose k}{\frac {(n-1)!}{(k-1)!}}={n \choose k}{n-1 \choose k-1}(n-k)!}
L
(
n
,
k
)
=
n
!
(
n
−
1
)
!
k
!
(
k
−
1
)
!
⋅
1
(
n
−
k
)
!
=
(
n
!
k
!
)
2
k
n
(
n
−
k
)
!
{\displaystyle L(n,k)={\frac {n!(n-1)!}{k!(k-1)!}}\cdot {\frac {1}{(n-k)!}}=\left({\frac {n!}{k!}}\right)^{2}{\frac {k}{n(n-k)!}}}
k
(
k
+
1
)
L
(
n
,
k
+
1
)
=
(
n
−
k
)
L
(
n
,
k
)
{\displaystyle k(k+1)L(n,k+1)=(n-k)L(n,k)}
k
>
0
{\displaystyle k>0}
Recurrence relations
The Lah numbers satisfy the recurrence relations
L
(
n
+
1
,
k
)
=
(
n
+
k
)
L
(
n
,
k
)
+
L
(
n
,
k
−
1
)
=
k
(
k
+
1
)
L
(
n
,
k
+
1
)
+
2
k
L
(
n
,
k
)
+
L
(
n
,
k
−
1
)
{\displaystyle {\begin{aligned}L(n+1,k)&=(n+k)L(n,k)+L(n,k-1)\\&=k(k+1)L(n,k+1)+2kL(n,k)+L(n,k-1)\end{aligned}}}
L
(
n
,
0
)
=
δ
n
{\displaystyle L(n,0)=\delta _{n}}
Kronecker delta , and
L
(
n
,
k
)
=
0
{\displaystyle L(n,k)=0}
k
>
n
{\displaystyle k>n}
Exponential generating function
∑
n
≥
k
L
(
n
,
k
)
x
n
n
!
=
1
k
!
(
x
1
−
x
)
k
{\displaystyle \sum _{n\geq k}L(n,k){\frac {x^{n}}{n!}}={\frac {1}{k!}}\left({\frac {x}{1-x}}\right)^{k}}
Derivative of exp(1/x )
The n -th derivative of the function
e
1
x
{\displaystyle e^{\frac {1}{x}}}
d
n
d
x
n
e
1
x
=
(
−
1
)
n
∑
k
=
1
n
L
(
n
,
k
)
x
n
+
k
⋅
e
1
x
.
{\displaystyle {\frac {{\textrm {d}}^{n}}{{\textrm {d}}x^{n}}}e^{\frac {1}{x}}=(-1)^{n}\sum _{k=1}^{n}{\frac {L(n,k)}{x^{n+k}}}\cdot e^{\frac {1}{x}}.}
d
d
x
e
1
x
=
−
1
x
2
⋅
e
1
x
{\displaystyle {\frac {\textrm {d}}{{\textrm {d}}x}}e^{\frac {1}{x}}=-{\frac {1}{x^{2}}}\cdot e^{\frac {1}{x}}}
d
2
d
x
2
e
1
x
=
d
d
x
(
−
1
x
2
e
1
x
)
=
−
−
2
x
3
⋅
e
1
x
−
1
x
2
⋅
−
1
x
2
⋅
e
1
x
=
(
2
x
3
+
1
x
4
)
⋅
e
1
x
{\displaystyle {\frac {{\textrm {d}}^{2}}{{\textrm {d}}x^{2}}}e^{\frac {1}{x}}={\frac {\textrm {d}}{{\textrm {d}}x}}\left(-{\frac {1}{x^{2}}}e^{\frac {1}{x}}\right)=-{\frac {-2}{x^{3}}}\cdot e^{\frac {1}{x}}-{\frac {1}{x^{2}}}\cdot {\frac {-1}{x^{2}}}\cdot e^{\frac {1}{x}}=\left({\frac {2}{x^{3}}}+{\frac {1}{x^{4}}}\right)\cdot e^{\frac {1}{x}}}
d
3
d
x
3
e
1
x
=
d
d
x
(
(
2
x
3
+
1
x
4
)
⋅
e
1
x
)
=
(
−
6
x
4
+
−
4
x
5
)
⋅
e
1
x
+
(
2
x
3
+
1
x
4
)
⋅
−
1
x
2
⋅
e
1
x
=
−
(
6
x
4
+
6
x
5
+
1
x
6
)
⋅
e
1
x
{\displaystyle {\frac {{\textrm {d}}^{3}}{{\textrm {d}}x^{3}}}e^{\frac {1}{x}}={\frac {\textrm {d}}{{\textrm {d}}x}}\left(\left({\frac {2}{x^{3}}}+{\frac {1}{x^{4}}}\right)\cdot e^{\frac {1}{x}}\right)=\left({\frac {-6}{x^{4}}}+{\frac {-4}{x^{5}}}\right)\cdot e^{\frac {1}{x}}+\left({\frac {2}{x^{3}}}+{\frac {1}{x^{4}}}\right)\cdot {\frac {-1}{x^{2}}}\cdot e^{\frac {1}{x}}=-\left({\frac {6}{x^{4}}}+{\frac {6}{x^{5}}}+{\frac {1}{x^{6}}}\right)\cdot e^{\frac {1}{x}}}
Link to Laguerre polynomials
Generalized Laguerre polynomials
L
n
(
α
)
(
x
)
{\displaystyle L_{n}^{(\alpha )}(x)}
α
=
−
1
{\displaystyle \alpha =-1}
n
!
L
n
(
−
1
)
(
x
)
=
∑
k
=
0
n
L
(
n
,
k
)
(
−
x
)
k
{\displaystyle n!L_{n}^{(-1)}(x)=\sum _{k=0}^{n}L(n,k)(-x)^{k}}
Laguerre polynomial in Umbral calculus convention.
Practical application
In recent years, Lah numbers have been used in steganography for hiding data in images. Compared to alternatives such as DCT , DFT and DWT , it has lower complexity of calculation—
O
(
n
log
n
)
{\displaystyle O(n\log n)}
chromatic dispersion .
In Lah-Laguerre optics , such an approach tremendously speeds up optimization problems.
See also
References
Lah, Ivo (1954). "A new kind of numbers and its application in the actuarial mathematics". Boletim do Instituto dos Actuários Portugueses . 9 : 7–15.
John Riordan, Introduction to Combinatorial Analysis , Princeton University Press (1958, reissue 1980) ISBN 978-0-691-02365-6 (reprinted again in 2002 by Dover Publications).
Petkovsek, Marko; Pisanski, Tomaz (Fall 2007). "Combinatorial Interpretation of Unsigned Stirling and Lah Numbers". Pi Mu Epsilon Journal . 12 (7): 417–424. JSTOR 24340704 .
Comtet, Louis (1974). Advanced Combinatorics 156 . ISBN 9789027703804
Shattuck, Mark (2014). "Generalized r-Lah numbers". arXiv :1412.8721 .
Nyul, Gábor; Rácz, Gabriella (2015-10-06). "The r-Lah numbers" . Discrete Mathematics . Seventh Czech-Slovak International Symposium on Graph Theory, Combinatorics, Algorithms and Applications, Košice 2013. 338 (10): 1660–1666. doi :10.1016/j.disc.2014.03.029 . hdl :2437/213886 . ISSN 0012-365X .
Daboul, Siad; Mangaldan, Jan; Spivey, Michael Z.; Taylor, Peter J. (2013). "The Lah Numbers and the nth Derivative of
e
1
x
{\displaystyle e^{1 \over x}}
Mathematics Magazine . 86 (1): 39–47. doi :10.4169/math.mag.86.1.039 . JSTOR 10.4169/math.mag.86.1.039 . S2CID 123113404 .
Rota, Gian-Carlo; Kahaner, D; Odlyzko, A (1973-06-01). "On the foundations of combinatorial theory. VIII. Finite operator calculus" . Journal of Mathematical Analysis and Applications . 42 (3): 684–760. doi :10.1016/0022-247X(73)90172-8 . ISSN 0022-247X .
Ghosal, Sudipta Kr; Mukhopadhyay, Souradeep; Hossain, Sabbir; Sarkar, Ram (2020). "Application of Lah Transform for Security and Privacy of Data through Information Hiding in Telecommunication". Transactions on Emerging Telecommunications Technologies . 32 (2). doi :10.1002/ett.3984 . S2CID 225866797 .
"Image Steganography-using-Lah-Transform" . MathWorks . 5 June 2020.Popmintchev, Dimitar; Wang, Siyang; Xiaoshi, Zhang; Stoev, Ventzislav; Popmintchev, Tenio (2022-10-24). "Analytical Lah-Laguerre optical formalism for perturbative chromatic dispersion" . Optics Express 30 (22): 40779–40808. Bibcode :2022OExpr..3040779P . doi :10.1364/OE.457139 . PMID 36299007 .
Popmintchev, Dimitar; Wang, Siyang; Xiaoshi, Zhang; Stoev, Ventzislav; Popmintchev, Tenio (2020-08-30). "Theory of the Chromatic Dispersion, Revisited". arXiv :2011.00066 .
External links
The signed and unsigned Lah numbers are respectively (sequence A008297 in the OEIS ) and (sequence A105278 in the OEIS ) Classes of natural numbers Possessing a specific set of other numbers
Expressible via specific sums
Categories :
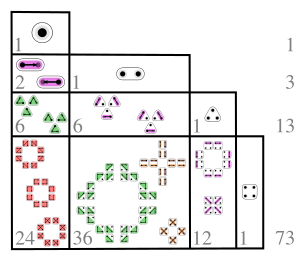
 are given by the formula involving the
are given by the formula involving the 
 .
.
 elements can be
elements can be  nonempty linearly ordered
nonempty linearly ordered  , the Lah number
, the Lah number  is equal to the
is equal to the  in the interpretation above, the only partition of
in the interpretation above, the only partition of  into 1 set can have its set ordered in 6 ways:
into 1 set can have its set ordered in 6 ways:
 is equal to 6, because there are six partitions of
is equal to 6, because there are six partitions of 
 is always 1 because the only way to partition
is always 1 because the only way to partition  into
into  non-empty subsets results in subsets of size 1, that can only be permuted in one way.
In the more recent literature,
non-empty subsets results in subsets of size 1, that can only be permuted in one way.
In the more recent literature, 
 (sequence
(sequence  represent the
represent the  and let
and let  represent the
represent the  . The Lah numbers are the coefficients that express each of these families of polynomials in terms of the other. Explicitly,
. The Lah numbers are the coefficients that express each of these families of polynomials in terms of the other. Explicitly, and
and For example,
For example, and
and
 ,
,  , and
, and  .
.
 where
where  are the
are the  are the
are the 

 , for
, for  .
. where
where  , the
, the  for all
for all  .
.

 can be expressed with the Lah numbers, as follows
can be expressed with the Lah numbers, as follows For example,
For example,



 are linked to Lah numbers upon setting
are linked to Lah numbers upon setting 
 This formula is the default
This formula is the default  —of their integer coefficients.
The Lah and Laguerre transforms naturally arise in the perturbative description of the
—of their integer coefficients.
The Lah and Laguerre transforms naturally arise in the perturbative description of the  ". Mathematics Magazine. 86 (1): 39–47.
". Mathematics Magazine. 86 (1): 39–47.