| Part of a series on | |||||||
| Continuum mechanics | |||||||
|---|---|---|---|---|---|---|---|
| Fick's laws of diffusion | |||||||
Laws
|
|||||||
| Solid mechanics | |||||||
Fluid mechanics
|
|||||||
Rheology
|
|||||||
| Scientists | |||||||
Fluid mechanics is the branch of physics concerned with the mechanics of fluids (liquids, gases, and plasmas) and the forces on them. It has applications in a wide range of disciplines, including mechanical, aerospace, civil, chemical, and biomedical engineering, as well as geophysics, oceanography, meteorology, astrophysics, and biology.
It can be divided into fluid statics, the study of fluids at rest; and fluid dynamics, the study of the effect of forces on fluid motion. It is a branch of continuum mechanics, a subject which models matter without using the information that it is made out of atoms; that is, it models matter from a macroscopic viewpoint rather than from microscopic.
Fluid mechanics, especially fluid dynamics, is an active field of research, typically mathematically complex. Many problems are partly or wholly unsolved and are best addressed by numerical methods, typically using computers. A modern discipline, called computational fluid dynamics (CFD), is devoted to this approach. Particle image velocimetry, an experimental method for visualizing and analyzing fluid flow, also takes advantage of the highly visual nature of fluid flow.
History
Main article: History of fluid mechanics For a chronological guide, see Timeline of fluid and continuum mechanics.The study of fluid mechanics goes back at least to the days of ancient Greece, when Archimedes investigated fluid statics and buoyancy and formulated his famous law known now as the Archimedes' principle, which was published in his work On Floating Bodies—generally considered to be the first major work on fluid mechanics. Iranian scholar Abu Rayhan Biruni and later Al-Khazini applied experimental scientific methods to fluid mechanics. Rapid advancement in fluid mechanics began with Leonardo da Vinci (observations and experiments), Evangelista Torricelli (invented the barometer), Isaac Newton (investigated viscosity) and Blaise Pascal (researched hydrostatics, formulated Pascal's law), and was continued by Daniel Bernoulli with the introduction of mathematical fluid dynamics in Hydrodynamica (1739).
Inviscid flow was further analyzed by various mathematicians (Jean le Rond d'Alembert, Joseph Louis Lagrange, Pierre-Simon Laplace, Siméon Denis Poisson) and viscous flow was explored by a multitude of engineers including Jean Léonard Marie Poiseuille and Gotthilf Hagen. Further mathematical justification was provided by Claude-Louis Navier and George Gabriel Stokes in the Navier–Stokes equations, and boundary layers were investigated (Ludwig Prandtl, Theodore von Kármán), while various scientists such as Osborne Reynolds, Andrey Kolmogorov, and Geoffrey Ingram Taylor advanced the understanding of fluid viscosity and turbulence.
Main branches
Fluid statics
Main article: Fluid staticsFluid statics or hydrostatics is the branch of fluid mechanics that studies fluids at rest. It embraces the study of the conditions under which fluids are at rest in stable equilibrium; and is contrasted with fluid dynamics, the study of fluids in motion. Hydrostatics offers physical explanations for many phenomena of everyday life, such as why atmospheric pressure changes with altitude, why wood and oil float on water, and why the surface of water is always level whatever the shape of its container. Hydrostatics is fundamental to hydraulics, the engineering of equipment for storing, transporting and using fluids. It is also relevant to some aspects of geophysics and astrophysics (for example, in understanding plate tectonics and anomalies in the Earth's gravitational field), to meteorology, to medicine (in the context of blood pressure), and many other fields.
Fluid dynamics
Main article: Fluid dynamicsFluid dynamics is a subdiscipline of fluid mechanics that deals with fluid flow—the science of liquids and gases in motion. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves calculating various properties of the fluid, such as velocity, pressure, density, and temperature, as functions of space and time. It has several subdisciplines itself, including aerodynamics (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and movements on aircraft, determining the mass flow rate of petroleum through pipelines, predicting evolving weather patterns, understanding nebulae in interstellar space and modeling explosions. Some fluid-dynamical principles are used in traffic engineering and crowd dynamics.
Relationship to continuum mechanics
Fluid mechanics is a subdiscipline of continuum mechanics, as illustrated in the following table.
| Continuum mechanics The study of the physics of continuous materials |
Solid mechanics The study of the physics of continuous materials with a defined rest shape. |
Elasticity Describes materials that return to their rest shape after applied stresses are removed. | |
| Plasticity Describes materials that permanently deform after a sufficient applied stress. |
Rheology The study of materials with both solid and fluid characteristics. | ||
| Fluid mechanics The study of the physics of continuous materials which deform when subjected to a force. |
Non-Newtonian fluid Do not undergo strain rates proportional to the applied shear stress. | ||
| Newtonian fluids undergo strain rates proportional to the applied shear stress. | |||
In a mechanical view, a fluid is a substance that does not support shear stress; that is why a fluid at rest has the shape of its containing vessel. A fluid at rest has no shear stress.
Assumptions
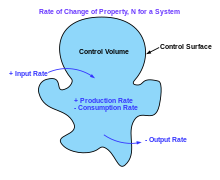
The assumptions inherent to a fluid mechanical treatment of a physical system can be expressed in terms of mathematical equations. Fundamentally, every fluid mechanical system is assumed to obey:
For example, the assumption that mass is conserved means that for any fixed control volume (for example, a spherical volume)—enclosed by a control surface—the rate of change of the mass contained in that volume is equal to the rate at which mass is passing through the surface from outside to inside, minus the rate at which mass is passing from inside to outside. This can be expressed as an equation in integral form over the control volume.
The continuum assumption is an idealization of continuum mechanics under which fluids can be treated as continuous, even though, on a microscopic scale, they are composed of molecules. Under the continuum assumption, macroscopic (observed/measurable) properties such as density, pressure, temperature, and bulk velocity are taken to be well-defined at "infinitesimal" volume elements—small in comparison to the characteristic length scale of the system, but large in comparison to molecular length scale. Fluid properties can vary continuously from one volume element to another and are average values of the molecular properties. The continuum hypothesis can lead to inaccurate results in applications like supersonic speed flows, or molecular flows on nano scale. Those problems for which the continuum hypothesis fails can be solved using statistical mechanics. To determine whether or not the continuum hypothesis applies, the Knudsen number, defined as the ratio of the molecular mean free path to the characteristic length scale, is evaluated. Problems with Knudsen numbers below 0.1 can be evaluated using the continuum hypothesis, but molecular approach (statistical mechanics) can be applied to find the fluid motion for larger Knudsen numbers.
Navier–Stokes equations
Main article: Navier–Stokes equationsThe Navier–Stokes equations (named after Claude-Louis Navier and George Gabriel Stokes) are differential equations that describe the force balance at a given point within a fluid. For an incompressible fluid with vector velocity field , the Navier–Stokes equations are
- .
These differential equations are the analogues for deformable materials to Newton's equations of motion for particles – the Navier–Stokes equations describe changes in momentum (force) in response to pressure and viscosity, parameterized by the kinematic viscosity . Occasionally, body forces, such as the gravitational force or Lorentz force are added to the equations.
Solutions of the Navier–Stokes equations for a given physical problem must be sought with the help of calculus. In practical terms, only the simplest cases can be solved exactly in this way. These cases generally involve non-turbulent, steady flow in which the Reynolds number is small. For more complex cases, especially those involving turbulence, such as global weather systems, aerodynamics, hydrodynamics and many more, solutions of the Navier–Stokes equations can currently only be found with the help of computers. This branch of science is called computational fluid dynamics.
Inviscid and viscous fluids
An inviscid fluid has no viscosity, . In practice, an inviscid flow is an idealization, one that facilitates mathematical treatment. In fact, purely inviscid flows are only known to be realized in the case of superfluidity. Otherwise, fluids are generally viscous, a property that is often most important within a boundary layer near a solid surface, where the flow must match onto the no-slip condition at the solid. In some cases, the mathematics of a fluid mechanical system can be treated by assuming that the fluid outside of boundary layers is inviscid, and then matching its solution onto that for a thin laminar boundary layer.
For fluid flow over a porous boundary, the fluid velocity can be discontinuous between the free fluid and the fluid in the porous media (this is related to the Beavers and Joseph condition). Further, it is useful at low subsonic speeds to assume that gas is incompressible—that is, the density of the gas does not change even though the speed and static pressure change.
Newtonian versus non-Newtonian fluids
A Newtonian fluid (named after Isaac Newton) is defined to be a fluid whose shear stress is linearly proportional to the velocity gradient in the direction perpendicular to the plane of shear. This definition means regardless of the forces acting on a fluid, it continues to flow. For example, water is a Newtonian fluid, because it continues to display fluid properties no matter how much it is stirred or mixed. A slightly less rigorous definition is that the drag of a small object being moved slowly through the fluid is proportional to the force applied to the object. (Compare friction). Important fluids, like water as well as most gasses, behave—to good approximation—as a Newtonian fluid under normal conditions on Earth.
By contrast, stirring a non-Newtonian fluid can leave a "hole" behind. This will gradually fill up over time—this behavior is seen in materials such as pudding, oobleck, or sand (although sand isn't strictly a fluid). Alternatively, stirring a non-Newtonian fluid can cause the viscosity to decrease, so the fluid appears "thinner" (this is seen in non-drip paints). There are many types of non-Newtonian fluids, as they are defined to be something that fails to obey a particular property—for example, most fluids with long molecular chains can react in a non-Newtonian manner.
Equations for a Newtonian fluid
Main article: Newtonian fluidThe constant of proportionality between the viscous stress tensor and the velocity gradient is known as the viscosity. A simple equation to describe incompressible Newtonian fluid behavior is
where
- is the shear stress exerted by the fluid ("drag"),
- is the fluid viscosity—a constant of proportionality, and
- is the velocity gradient perpendicular to the direction of shear.
For a Newtonian fluid, the viscosity, by definition, depends only on temperature, not on the forces acting upon it. If the fluid is incompressible the equation governing the viscous stress (in Cartesian coordinates) is
where
- is the shear stress on the face of a fluid element in the direction
- is the velocity in the direction
- is the direction coordinate.
If the fluid is not incompressible the general form for the viscous stress in a Newtonian fluid is
where is the second viscosity coefficient (or bulk viscosity). If a fluid does not obey this relation, it is termed a non-Newtonian fluid, of which there are several types. Non-Newtonian fluids can be either plastic, Bingham plastic, pseudoplastic, dilatant, thixotropic, rheopectic, viscoelastic.
In some applications, another rough broad division among fluids is made: ideal and non-ideal fluids. An ideal fluid is non-viscous and offers no resistance whatsoever to a shearing force. An ideal fluid really does not exist, but in some calculations, the assumption is justifiable. One example of this is the flow far from solid surfaces. In many cases, the viscous effects are concentrated near the solid boundaries (such as in boundary layers) while in regions of the flow field far away from the boundaries the viscous effects can be neglected and the fluid there is treated as it were inviscid (ideal flow). When the viscosity is neglected, the term containing the viscous stress tensor in the Navier–Stokes equation vanishes. The equation reduced in this form is called the Euler equation.
See also
- Transport phenomena
- Aerodynamics
- Applied mechanics
- Bernoulli's principle
- Communicating vessels
- Computational fluid dynamics
- Compressor map
- Secondary flow
- Different types of boundary conditions in fluid dynamics
- Fluid–structure interaction
- Immersed boundary method
- Stochastic Eulerian Lagrangian method
- Stokesian dynamics
- Smoothed-particle hydrodynamics
References
- ^ White, Frank M. (2011). Fluid Mechanics (7th ed.). McGraw-Hill. ISBN 978-0-07-352934-9.
- Tu, Jiyuan; Yeoh, Guan Heng; Liu, Chaoqun (Nov 21, 2012). Computational Fluid Dynamics: A Practical Approach. Butterworth-Heinemann. ISBN 978-0080982434.
- Mariam Rozhanskaya and I. S. Levinova (1996), "Statics", p. 642,
- Batchelor, C. K., & Batchelor, G. K. (2000). An introduction to fluid dynamics. Cambridge University Press.
- Bertin, J. J., & Smith, M. L. (1998). Aerodynamics for engineers (Vol. 5). Upper Saddle River, NJ: Prentice Hall.
- Anderson Jr, J. D. (2010). Fundamentals of aerodynamics. Tata McGraw-Hill Education.
- Houghton, E. L., & Carpenter, P. W. (2003). Aerodynamics for engineering students. Elsevier.
- Milne-Thomson, L. M. (1973). Theoretical aerodynamics. Courier Corporation.
- Milne-Thomson, L. M. (1996). Theoretical hydrodynamics. Courier Corporation.
- Birkhoff, G. (2015). Hydrodynamics. Princeton University Press.
- ^ Batchelor, George K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press. p. 74. ISBN 0-521-66396-2.
- Greenkorn, Robert (3 October 2018). Momentum, Heat, and Mass Transfer Fundamentals. CRC Press. p. 18. ISBN 978-1-4822-9297-8.
- Constantin, P., & Foias, C. (1988). Navier-stokes equations. University of Chicago Press.
- Temam, R. (2001). Navier-Stokes equations: theory and numerical analysis (Vol. 343). American Mathematical Society.
- Foias, C., Manley, O., Rosa, R., & Temam, R. (2001). Navier-Stokes equations and turbulence (Vol. 83). Cambridge University Press.
- Girault, V., & Raviart, P. A. (2012). Finite element methods for Navier-Stokes equations: theory and algorithms (Vol. 5). Springer Science & Business Media.
- Anderson, J. D., & Wendt, J. (1995). Computational fluid dynamics (Vol. 206). New York: McGraw-Hill.
- Chung, T. J. (2010). Computational fluid dynamics. Cambridge University Press.
- Blazek, J. (2015). Computational fluid dynamics: principles and applications. Butterworth-Heinemann.
- Wesseling, P. (2009). Principles of computational fluid dynamics (Vol. 29). Springer Science & Business Media.
- Anderson, D., Tannehill, J. C., & Pletcher, R. H. (2016). Computational fluid mechanics and heat transfer. Taylor & Francis.
- Kundu, Pijush K.; Cohen, Ira M.; Dowling, David R. (27 March 2015). "10". Fluid Mechanics (6th ed.). Academic Press. ISBN 978-0124059351.
Further reading
- Falkovich, Gregory (2011), Fluid Mechanics (A short course for physicists), Cambridge University Press, doi:10.1017/CBO9780511794353, ISBN 978-1-107-00575-4
- Kundu, Pijush K.; Cohen, Ira M. (2008), Fluid Mechanics (4th revised ed.), Academic Press, ISBN 978-0-12-373735-9
- Currie, I. G. (1974), Fundamental Mechanics of Fluids, McGraw-Hill, Inc., ISBN 0-07-015000-1
- Massey, B.; Ward-Smith, J. (2005), Mechanics of Fluids (8th ed.), Taylor & Francis, ISBN 978-0-415-36206-1
- Nazarenko, Sergey (2014), Fluid Dynamics via Examples and Solutions, CRC Press (Taylor & Francis group), ISBN 978-1-43-988882-7
External links
- Free Fluid Mechanics books
- Annual Review of Fluid Mechanics. Archived 2009-01-19 at the Wayback Machine.
- CFDWiki – the Computational Fluid Dynamics reference wiki.
- Educational Particle Image Velocimetry Archived 2017-08-03 at the Wayback Machine – resources and demonstrations
| Major branches of physics | |
|---|---|
| Divisions | |
| Approaches | |
| Classical | |
| Modern | |
| Interdisciplinary | |
| Related | |

 , the Navier–Stokes equations are
, the Navier–Stokes equations are
 .
. and viscosity, parameterized by the
and viscosity, parameterized by the  . Occasionally,
. Occasionally,  . In practice, an inviscid flow is an
. In practice, an inviscid flow is an 
 is the shear stress exerted by the fluid ("
is the shear stress exerted by the fluid (" is the fluid viscosity—a constant of proportionality, and
is the fluid viscosity—a constant of proportionality, and is the velocity gradient perpendicular to the direction of shear.
is the velocity gradient perpendicular to the direction of shear.
 is the shear stress on the
is the shear stress on the  face of a fluid element in the
face of a fluid element in the  direction
direction is the velocity in the
is the velocity in the  is the
is the 
 is the second viscosity coefficient (or bulk viscosity). If a fluid does not obey this relation, it is termed a
is the second viscosity coefficient (or bulk viscosity). If a fluid does not obey this relation, it is termed a  in the Navier–Stokes equation vanishes. The equation reduced in this form is called the
in the Navier–Stokes equation vanishes. The equation reduced in this form is called the