Misplaced Pages

McCay cubic

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Plane curve unique to a given triangle

In Euclidean geometry, the McCay cubic (also called M'Cay cubic or Griffiths cubic) is a cubic plane curve in the plane of a reference triangle and associated with it. It is the third cubic curve in Bernard Gilbert's Catalogue of Triangle Cubics and it is assigned the identification number K003.

Definition

  Reference triangle △ABC   Nine-point circle of △ABC   Pedal triangle of point P   Pedal circle (circumcircle of pedal triangle) of P   McCay cubic: locus of P such that the pedal circle and nine point circle are tangent

The McCay cubic can be defined by locus properties in several ways. For example, the McCay cubic is the locus of a point P such that the pedal circle of P is tangent to the nine-point circle of the reference triangle △ABC. The McCay cubic can also be defined as the locus of point P such that the circumcevian triangle of P and △ABC are orthologic.

Equation of the McCay cubic

The equation of the McCay cubic in barycentric coordinates x : y : z {\displaystyle x:y:z} is

∑ cyclic ( a 2 ( b 2 + c 2 − a 2 ) x ( c 2 y 2 − b 2 z 2 ) ) = 0. {\displaystyle \sum _{\text{cyclic}}(a^{2}(b^{2}+c^{2}-a^{2})x(c^{2}y^{2}-b^{2}z^{2}))=0.}

The equation in trilinear coordinates α : β : γ {\displaystyle \alpha :\beta :\gamma } is

α ( β 2 − γ 2 ) cos ⁡ A + β ( γ 2 − α 2 ) cos ⁡ B + γ ( α 2 − β 2 ) cos ⁡ C = 0 {\displaystyle \alpha (\beta ^{2}-\gamma ^{2})\cos A+\beta (\gamma ^{2}-\alpha ^{2})\cos B+\gamma (\alpha ^{2}-\beta ^{2})\cos C=0}

McCay cubic as a stelloid

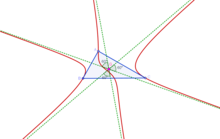
McCay cubic with its three concurring asymptotes

A stelloid is a cubic that has three real concurring asymptotes making 60° angles with one another. McCay cubic is a stelloid in which the three asymptotes concur at the centroid of triangle ABC. A circum-stelloid having the same asymptotic directions as those of McCay cubic and concurring at a certain (finite) is called McCay stelloid. The point where the asymptoptes concur is called the "radial center" of the stelloid. Given a finite point X there is one and only one McCay stelloid with X as the radial center.

References

  1. Weisstein, Eric W. "M'Cay Cubic". MathWorld-A Wolfram Web Resource. Wolfram Research, Inc. Retrieved 5 December 2021.
  2. ^ Bernard Gilbert. "K003 McCay Cubic = Griffiths Cubic". Cubics in the Triangle Plane. Bernard Gilbert. Retrieved 5 December 2021.
  3. John Griffiths. Mathematical Questions and Solutions from the Educational Times 2 (1902) 109, and 3 (1903) 29.
  4. Bernard Gilbert. "McCay Stelloids" (PDF). Catalogue of Triangle Cubics. Bernard Gilbert. Retrieved 25 December 2021.
Categories: