
The Mesoamerican Long Count calendar is a non-repeating base-20 and base-18 calendar used by pre-Columbian Mesoamerican cultures, most notably the Maya. For this reason, it is often known as the Maya Long Count calendar. Using a modified vigesimal tally, the Long Count calendar identifies a day by counting the number of days passed since a mythical creation date that corresponds to August 11, 3114 BCE in the proleptic Gregorian calendar. The Long Count calendar was widely used on monuments.
Background
The two most widely used calendars in pre-Columbian Mesoamerica were the 260-day Tzolkʼin and the 365-day Haabʼ. The equivalent Aztec calendars are known in Nahuatl as the Tonalpohualli and Xiuhpohualli, respectively.
The combination of a Haabʼ and a Tzolkʼin date identifies a day in a combination which does not occur again for 18,980 days (52 Haabʼ cycles of 365 days equals 73 Tzolkʼin cycles of 260 days, approximately 52 years), a period known as the Calendar Round. To identify days over periods longer than this, Mesoamericans used the Long Count calendar.
Long Count periods
| This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (August 2017) (Learn how and when to remove this message) |

The Long Count calendar identifies a date by counting the number of days from a starting date that is generally calculated to be August 11, 3114 BCE in the proleptic Gregorian calendar or September 6 in the Julian calendar (or −3113 in astronomical year numbering). There has been much debate over the precise correlation between the Western calendars and the Long Count calendars. The August 11 date is based on the GMT correlation.
The completion of 13 bʼakʼtuns (August 11, 3114 BCE) marks the Creation of the world of human beings according to the Maya. On this day, Raised-up-Sky-Lord caused three stones to be set by associated gods at Lying-Down-Sky, First-Three-Stone-Place. Because the sky still lay on the primordial sea, it was black. The setting of the three stones centered the cosmos which allowed the sky to be raised, revealing the sun.
Rather than using a base 10 scheme, the Long Count days were tallied in a modified base-20 scheme. In a pure base 20 scheme, 0.0.0.1.5 is equal to 25 and 0.0.0.2.0 is equal to 40. The Long Count is not pure base-20, however, since the second digit from the right (and only that digit) rolls over to zero when it reaches 18. Thus 0.0.1.0.0 does not represent 400 days, but rather only 360 days and 0.0.0.17.19 represents 359 days.
The name bʼakʼtun was invented by modern scholars. The numbered Long Count was no longer in use by the time the Spanish arrived in the Yucatán Peninsula, although unnumbered kʼatuns and tuns were still in use. Instead the Maya were using an abbreviated Short Count.
| Long Count unit |
Long Count period |
Days | Approximate Solar Years |
|---|---|---|---|
| 1 Kʼin | 1 | ||
| 1 Winal | 20 Kʼin | 20 | |
| 1 Tun | 18 Winal | 360 | 1 |
| 1 Kʼatun | 20 Tun | 7,200 | 20 |
| 1 Bʼakʼtun | 20 Kʼatun | 144,000 | 394 |
| 1 Piktun | 20 Bʼakʼtun | 2,880,000 | 7,885 |
| 1 Kalabtun | 20 Piktun | 57,600,000 | 157,704 |
| 1 Kʼinchiltun | 20 Kalabtun | 1,152,000,000 | 3,154,071 |
| 1 Alautun | 20 Kʼinchiltun | 23,040,000,000 | 63,081,429 |
| 1 Hablatun | 20 Alautun | 460,800,000,000 | 1,261,628,585 |
Mesoamerican numerals
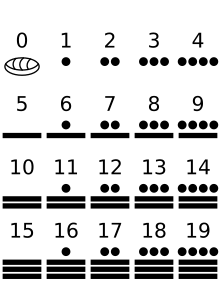
Long Count dates are written with Mesoamerican numerals, as shown on this table. A dot represents 1 while a bar equals 5. The shell glyph was used to represent the zero concept. The Long Count calendar required the use of zero as a place-holder and presents one of the earliest uses of the zero concept in history.
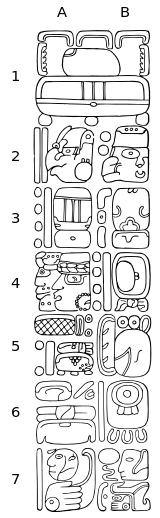
On Maya monuments, the Long Count syntax is more complex. The date sequence is given once, at the beginning of the inscription and opens with the so-called ISIG (Introductory Series Initial Glyph) which reads tzik-a(h) habʼ ("revered was the year-count with the patron "). Next come the 5 digits of the Long Count, followed by the Calendar Round (tzolkʼin and Haabʼ) and supplementary series. The supplementary series is optional and contains lunar data, for example, the age of the moon on the day and the calculated length of current lunation. The text then continues with whatever activity occurred on that date.
A drawing of a full Maya Long Count inscription is shown below.
Earliest Long Counts
The earliest contemporaneous Long Count inscription yet discovered is on Stela 2 at Chiapa de Corzo, Chiapas, Mexico, showing a date of 36 BCE, although Stela 2 from Takalik Abaj, Guatemala might be earlier. Takalik Abaj Stela 2's highly battered Long Count inscription shows 7 bak'tuns, followed by k'atuns with a tentative 6 coefficient, but that could also be 11 or 16, giving the range of possible dates to fall between 236 and 19 BCE.
Although Takalik Abaj Stela 2 remains controversial, this table includes it, as well as six other artifacts with the eight oldest Long Count inscriptions according to Dartmouth professor Vincent H. Malmström (two of the artifacts contain two dates and Malmström does not include Takalik Abaj Stela 2). Interpretations of inscriptions on some artifacts differ.
| Archaeological site | Name | Gregorian date
GMT (584283) correlation |
Long Count | Location |
|---|---|---|---|---|
| Takalik Abaj | Stela 2 | 236 – 19 BCE | 7.(6,11,16).?.?.? | Retalhuleu, Guatemala |
| Chiapa de Corzo | Stela 2 | December 6, 36 BCE or October 9, 182 CE |
7.16.3.2.13 or 8.7.3.2.13 |
Chiapas, Mexico |
| Tres Zapotes | Stela C | September 1, 32 BCE | 7.16.6.16.18 | Veracruz, Mexico |
| El Baúl | Stela 1 | 11 – 37 CE | 7.18.9.7.12, 7.18.14.8.12, 7.19.7.8.12, or 7.19.15.7.12 |
Escuintla, Guatemala |
| Takalik Abaj | Stela 5 | August 31, 83 CE or May 19, 103 CE |
8.2.2.10.15 or 8.3.2.10.15 |
Retalhuleu, Guatemala |
| Takalik Abaj | Stela 5 | June 3, 126 CE | 8.4.5.17.11 | Retalhuleu, Guatemala |
| La Mojarra | Stela 1 | May 19, 143 CE | 8.5.3.3.5 | Veracruz, Mexico |
| La Mojarra | Stela 1 | July 11, 156 CE | 8.5.16.9.7 | Veracruz, Mexico |
| Near La Mojarra | Tuxtla Statuette | March 12, 162 CE | 8.6.2.4.17 | Veracruz, Mexico |
Of the six sites, three are on the western edge of the Maya homeland and three are several hundred kilometers further west, leading some researchers to believe that the Long Count calendar predates the Maya. La Mojarra Stela 1, the Tuxtla Statuette, Tres Zapotes Stela C and Chiapa Stela 2 are all inscribed in an Epi-Olmec, not Maya, style. El Baúl Stela 2, on the other hand, was created in the Izapan style.
The first unequivocally Maya artifact is Stela 29 from Tikal, with the Long Count date of 292 CE (8.12.14.8.15), more than 300 years after Stela 2 from Chiapa de Corzo.
More recently, with the discovery in Guatemala of the San Bartolo (Maya site) stone block text (c. 300 BCE), it has been argued that this text celebrates an upcoming time period ending celebration. This time period may have been projected to end sometime between 7.3.0.0.0 (295 BCE) and 7.5.0.0.0 (256 BCE). Besides being the earliest Maya hieroglyphic text so far uncovered, this would arguably be the earliest evidence to date of Long Count notation in Mesoamerica.
Correlations between Western calendars and the Long Count

This is the second oldest Long Count date yet discovered. The numerals 7.16.6.16.18 translate to September 1, 32 BCE (Gregorian). The glyphs surrounding the date are what is thought to be one of the few surviving examples of Epi-Olmec script.
The Maya and Western calendars are correlated by using a Julian day number (JDN) of the starting date of the current creation — 13.0.0.0.0, 4 Ajaw, 8 Kumkʼu. This is referred to as a "correlation constant". The generally accepted correlation constant is the Modified Thompson 2, "Goodman–Martinez–Thompson", or GMT correlation of 584,283 days. Using the GMT correlation, the current creation started on September 6, −3113 (Julian astronomical) – August 11, 3114 BCE in the Proleptic Gregorian calendar. The study of correlating the Maya and western calendar is referred to as the correlation question. The GMT correlation is also called the 11.16 correlation.
In Breaking the Maya Code, Michael D. Coe writes: "In spite of oceans of ink that have been spilled on the subject, there now is not the slightest chance that these three scholars (conflated to G-M-T when talking about the correlation) were not right ...". The evidence for the GMT correlation is historical, astronomical and archaeological:
Historical: Calendar Round dates with a corresponding Julian date are recorded in Diego de Landa's Relación de las cosas de Yucatán (written circa 1566), the Chronicle of Oxcutzkab and the books of Chilam Balam. De Landa records a date that is a Tun ending in the Short Count. Oxkutzcab contains 12 Tun endings. Bricker and Bricker find that only the GMT correlation is consistent with these dates. The Book of Chilam Balam of Chumayel contains the only colonial reference to classic long-count dates. The Julian calendar date of 11.16.0.0.0 (November 2, 1539) confirms the GMT correlation.
The Annals of the Cakchiquels contains numerous Tzolkʼin dates correlated with European dates. These confirm the GMT correlation. Weeks, Sachse and Prager transcribed three divinatory calendars from highland Guatemala. They found that the 1772 calendar confirms the GMT correlation. The fall of the capital city of the Aztec Empire, Tenochtitlan, occurred on August 13, 1521. A number of different chroniclers wrote that the Tzolkʼin (Tonalpohualli) date of the event was 1 Snake.
Post-conquest scholars such as Sahagún and Durán recorded Tonalpohualli dates with a calendar date. Many indigenous communities in the Mexican states of Veracruz, Oaxaca and Chiapas and in Guatemala, principally those speaking the Mayan languages Ixil, Mam, Pokomchí and Quiché, keep the Tzolkʼin and in many cases the Haabʼ. These are all consistent with the GMT correlation. Munro Edmonsen studied 60 Mesoamerican calendars, 20 of which have known correlations to European calendars, and found remarkable consistency among them and that only the GMT correlation fits the historical, ethnographic and astronomical evidence.
Astronomical: Any correct correlation must match the astronomical content of classic inscriptions. The GMT correlation does an excellent job of matching lunar data in the supplementary series. For example: An inscription at the Temple of the Sun at Palenque records that on Long Count 9.16.4.10.8 there were 26 days completed in a 30-day lunation. This Long Count is also the entry date for the eclipse table of the Dresden Codex.
Using the third method, the Palenque system, the new moon would have been the first evening when one could look to the west after sunset and see the thin crescent moon. Given our modern ability to know exactly where to look, when the crescent Moon is favorably located, from an excellent site, on rare occasions, using binoculars or a telescope, observers can see and photograph the crescent moon less than one day after conjunction. Generally, most observers cannot see the new Moon with the naked eye until the first evening when the lunar phase day is at least 1.5. If one assumes that the new moon is the first day when the lunar phase day is at least 1.5 at six in the evening in time zone UTC−6 (the time zone of the Maya area), the GMT correlation will match many lunar inscriptions exactly. In this example the lunar phase day was 27.7 (26 days counting from zero) at 6 pm after a conjunction at 1:25 am October 10, 755 and a new Moon when the lunar phase day was 1.7 at 6 pm on October 11, 755 (Julian calendar). This works well for many but not all lunar inscriptions.
Modern astronomers refer to the conjunction of the Sun and Moon (the time when the Sun and Moon have the same ecliptic longitude) as the new moon. But Mesoamerican astronomy was observational, not theoretical. The people of Mesoamerica did not know about the Copernican nature of the solar system — they had no theoretical understanding of the orbital nature of the heavenly bodies. Some authors analyze the lunar inscriptions based on this modern understanding of the motions of the Moon but there is no evidence that the Mesoamericans shared it.
The first method seems to have been used for other inscriptions such as Quirgua stela E (9.17.0.0.0). By the third method, that stela should show a moon age of 26 days, but in fact it records a new moon. Using the GMT correlation at six AM in the time zone UTC−6, this would be 2.25 days before conjunction, so it could record the first day when one could not see the waning moon.
Fuls analysed these inscriptions and found strong evidence for the Palenque system and the GMT correlation; however, he cautioned: "Analysis of the Lunar Series shows that at least two different methods and formulas were used to calculate the moon's age and position in the six-month cycle ..." which gives eclipse seasons when the Moon is near its ascending or descending node and an eclipse is likely to occur. Dates converted using the GMT correlation agree closely with the Dresden Codex eclipse tables. The Dresden Codex contains a Venus table which records the heliacal risings of Venus. Using the GMT correlation these agree closely with modern astronomical calculations.
Archaeological: Various items that can be associated with specific Long Count dates have been isotope dated. In 1959 the University of Pennsylvania carbon dated samples from ten wood lintels from Tikal. These were carved with a date equivalent to 741 AD, using the GMT correlation. The average carbon date was 746±34 years. Recently one of these, Lintel 3 from Temple I, was analyzed again using more accurate methods and found to agree closely with the GMT correlation. In 2012, using modern AMS radiocarbon dating, a single beam from Tikal was dated, also strongly supporting the GMT.
If a proposed correlation only has to agree with one of these lines of evidence there could be numerous other possibilities. Astronomers have proposed many correlations, for example: Lounsbury, Fuls, et al., Böhm and Böhm and Stock.
Today, 12 January 2025 (UTC), in the Long Count is 13.0.12.4.5 (using GMT correlation).
| Name | Correlation |
|---|---|
| Bowditch | 394,483 |
| Willson | 438,906 |
| Smiley | 482,699 |
| Makemson | 489,138 |
| Modified Spinden | 489,383 |
| Spinden | 489,384 |
| Teeple | 492,622 |
| Dinsmoor | 497,879 |
| −4CR | 508,363 |
| −2CR | 546,323 |
| Stock | 556,408 |
| Goodman | 584,280 |
| Martinez–Hernandez | 584,281 |
| GMT | 584,283 |
| Modified Thompson 1 | 584,284 |
| Thompson (Lounsbury) | 584,285 |
| Pogo | 588,626 |
| +2CR | 622,243 |
| Böhm & Böhm | 622,261 |
| Kreichgauer | 626,927 |
| +4CR | 660,203 |
| Fuls, et al. | 660,208 |
| Hochleitner | 674,265 |
| Schultz | 677,723 |
| Escalona–Ramos | 679,108 |
| Vaillant | 679,183 |
| Weitzel | 774,078 |
| Long Count | (proleptic before 1582) Gregorian date GMT (584,283) correlation |
Julian day number |
|---|---|---|
| 0.0.0.0.0 (13.0.0.0.0) |
Mon, Aug 11, 3114 BCE | 584,283 |
| 1.0.0.0.0 | Thu, Nov 13, 2720 BCE | 728,283 |
| 2.0.0.0.0 | Sun, Feb 16, 2325 BCE | 872,283 |
| 3.0.0.0.0 | Wed, May 21, 1931 BCE | 1,016,283 |
| 4.0.0.0.0 | Sat, Aug 23, 1537 BCE | 1,160,283 |
| 5.0.0.0.0 | Tue, Nov 26, 1143 BCE | 1,304,283 |
| 6.0.0.0.0 | Fri, Feb 28, 748 BCE | 1,448,283 |
| 7.0.0.0.0 | Mon, Jun 3, 354 BCE | 1,592,283 |
| 8.0.0.0.0 | Thu, Sep 5, 41 CE | 1,736,283 |
| 9.0.0.0.0 | Sun, Dec 9, 435 | 1,880,283 |
| 10.0.0.0.0 | Wed, Mar 13, 830 | 2,024,283 |
| 11.0.0.0.0 | Sat, Jun 15, 1224 | 2,168,283 |
| 12.0.0.0.0 | Tue, Sep 18, 1618 | 2,312,283 |
| 13.0.0.0.0 | Fri, Dec 21, 2012 | 2,456,283 |
| 14.0.0.0.0 | Mon, Mar 26, 2407 | 2,600,283 |
| 15.0.0.0.0 | Thu, Jun 28, 2801 | 2,744,283 |
| 16.0.0.0.0 | Sun, Oct 1, 3195 | 2,888,283 |
| 17.0.0.0.0 | Wed, Jan 3, 3590 | 3,032,283 |
| 18.0.0.0.0 | Sat, Apr 7, 3984 | 3,176,283 |
| 19.0.0.0.0 | Tue, Jul 11, 4378 | 3,320,283 |
| 1.0.0.0.0.0 | Fri, Oct 13, 4772 | 3,464,283 |
2012 and the Long Count
Main article: 2012 phenomenonAccording to the Popol Vuh, a book compiling details of creation accounts known to the Kʼicheʼ Maya of the Colonial-era highlands, humankind lives in the fourth world. The Popol Vuh describes the first three creations that the gods failed in making and the creation of the successful fourth world where men were placed. In the Maya Long Count, the previous creation ended at the end of a 13th bʼakʼtun.
The previous creation ended on a Long Count of 12.19.19.17.19. Another 12.19.19.17.19 occurred on December 20, 2012 (Gregorian Calendar), followed by the start of the 14th bʼakʼtun, 13.0.0.0.0, on December 21, 2012. There are only two references to the current creation's 13th bʼakʼtun in the fragmentary Mayan corpus: Tortuguero Monument 6, part of a ruler's inscription and the recently discovered La Corona Hieroglyphic Stairway 2, Block V.
Maya inscriptions occasionally reference future predicted events or commemorations that would occur on dates that lie beyond 2012 (that is, beyond the completion of the 13th bʼakʼtun of the current era). Most of these are in the form of "distance dates" where some Long Count date is given, together with a Distance Number that is to be added to the Long Count date to arrive at this future date.
For example, on the west panel at the Temple of Inscriptions in Palenque, a section of the text projects into the future to the 80th Calendar Round (CR) 'anniversary' of the famous Palenque ruler Kʼinich Janaabʼ Pakal's accession to the throne (Pakal's accession occurred on a Calendar Round date 5 Lamat 1 Mol, at Long Count 9.9.2.4.8 equivalent to 27 July 615 CE in the proleptic Gregorian calendar). It does this by commencing with Pakal's birthdate 9.8.9.13.0 8 Ajaw 13 Pop (24 March 603 CE Gregorian) and adding to it the Distance Number 10.11.10.5.8.
This calculation arrives at the 80th Calendar Round since his accession, a day that also has a CR date of 5 Lamat 1 Mol, but which lies over 4,000 years in the future from Pakal's time—the day 21 October in the year 4772. The inscription notes that this day would fall eight days after the completion of the 1st piktun (since the creation or zero date of the Long Count system), where the piktun is the next-highest order above the bʼakʼtun in the Long Count. If the completion date of that piktun—13 October 4772—were to be written out in Long Count notation, it could be represented as 1.0.0.0.0.0. The 80th CR anniversary date, eight days later, would be 1.0.0.0.0.8 5 Lamat 1 Mol.
Despite the publicity generated by the 2012 date, Susan Milbrath, curator of Latin American Art and Archaeology at the Florida Museum of Natural History, stated that "We have no record or knowledge that would think the world would come to an end" in 2012. USA Today writes "'For the ancient Maya, it was a huge celebration to make it to the end of a whole cycle,' says Sandra Noble, executive director of the Foundation for the Advancement of Mesoamerican Studies in Crystal River, Florida. To render December 21, 2012, as a doomsday event or moment of cosmic shifting, she says, is 'a complete fabrication and a chance for a lot of people to cash in.'" "There will be another cycle," says E. Wyllys Andrews V, director of the Tulane University Middle American Research Institute (MARI). "We know the Maya thought there was one before this, and that implies they were comfortable with the idea of another one after this."
Converting between the Long Count and western calendars
Calculating a Western calendar date from a Long Count
It is important to know the difference between the Julian and Gregorian calendars when calculating a Western calendar date from a Long Count date.
Using as an example the Long Count date of 9.10.11.17.0 (Long Count date mentioned on the Palenque Palace Tablet), first calculate the number of days that have passed since the zero date (August 11, 3114 BCE; GMT correlation, in the Proleptic Gregorian calendar, September 6, −3113 Julian astronomical).
| 9 | × 144,000 | = 1,296,000 |
| 10 | × 7,200 | = 72,000 |
| 11 | × 360 | = 3,960 |
| 17 | × 20 | = 340 |
| 0 | × 1 | = 0 |
| Total days | = 1,372,300 |
Then add the GMT correlation to the total number of days.
- 1,372,300 + 584,283 = 1,956,583
This number is a Julian day.
To convert a Julian day to a Proleptic Gregorian calendar date:
From this number, subtract the nearest smaller Julian Day Number (in the table below), in this case 1,940,206, which corresponds to the year 600 CE.
| year | JDN: | year | JDN: |
|---|---|---|---|
| 1 | 1,721,060 | 1100 | 2,122,827 |
| 100 | 1,757,585 | 1200 | 2,159,351 |
| 200 | 1,794,109 | 1300 | 2,195,876 |
| 300 | 1,830,633 | 1400 | 2,232,400 |
| 400 | 1,867,157 | 1500 | 2,268,924 |
| 500 | 1,903,682 | 1600 | 2,305,448 |
| 600 | 1,940,206 | 1700 | 2,341,973 |
| 700 | 1,976,730 | 1800 | 2,378,497 |
| 800 | 2,013,254 | 1900 | 2,415,021 |
| 900 | 2,049,779 | 2000 | 2,451,545 |
| 1000 | 2,086,303 |
- 1,956,583 – 1,940,206 = 16,377
Next, divide this number by 365 days (vague year).
- 16,377 / 365 = 44.86849
The remainder is 44.86849 years, which is 44 years and 317 days. The full year date is 644 CE. Now calculate the month and day number, taking into account leap days over the 44 years. In the Gregorian Calendar, every fourth year is a leap year with the exception of centuries not evenly divisible by 400 (e.g. 100, 200, 300). When the year is divisible by 400 (e.g. 400, 800, etc.), do not add an extra day. The calculated year is 644 CE. The number of leap days, keeping in mind that the year 600 is not a leap year, is 10. Subtracting that from 317 remainder days is 307; in other words, the 307th day of the year 644 CE, which is November 3. To summarize: the Long Count date 9.10.11.17.0 corresponds to November 3, 644 CE, in the Proleptic Gregorian calendar.
To convert a Julian day to a Julian/Gregorian astronomical date (Proleptic Julian calendar before 46 BCE):
Use an astronomical algorithm such as the Method of Meeus to convert the Julian day to a Julian/Gregorian date with astronomical dating of negative years:
In this example:
input: Julian day J
J = J + 0.5 // 1,956,583.5
Z = integer part of J // 1,956,583
F = fraction part of J // 0.5
if Z < 2,299,161 then // Julian?
A = Z
else
alpha = floor((Z - 1,867,216.25) / 36,524.25) // 15
A = Z + 1 + alpha - floor(alpha / 4.0) // 2,436,129
// The floor operation rounds a decimal number down to the next lowest integer.
// For example, floor(1.5) = 1 and floor(−1.5) = -2
end if
B = A + 1524 // 1,958,107
C = floor((B - 122.1) / 365.25) // 5,360
D = floor(365.25 × C) // 1,957,740
E = floor((B - D) / 30.6001) // 11
day = B - D - floor(30.6001 × E) + F // 31.5
if E < 14 then
month = E - 1 // 10
else
month = E - 13
end if
if month > 2 then
year = C - 4716 // 644
else
year = C - 4715
end if
return (year, month, day)
In this example the Julian date is noon October 31, 644. The Method of Meeus is not valid for negative year numbers (astronomical), so another method such as the method of Peter Baum should be used.
Calculating a full Long Count date
| This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (August 2020) (Learn how and when to remove this message) |
A full Long Count date not only includes the five digits of the Long Count, but the 2 character Tzolkʼin and the two-character Haabʼ dates as well. The five digit Long Count can therefore be confirmed with the other four characters (the "calendar round date").
Taking as an example a Calendar Round date of 9.12.2.0.16 (Long Count) 5 Kibʼ (Tzolkʼin) 14 Yaxkʼin (Haabʼ). One can check whether this date is correct by the following calculation.
It is perhaps easier to find out how many days there are since 4 Ajaw 8 Kumkʼu and show how the date 5 Kibʼ 14 Yaxkʼin is derived.
| 9 | × 144000 | = 1296000 |
| 12 | × 7200 | = 86400 |
| 2 | × 360 | = 720 |
| 0 | × 20 | = 0 |
| 16 | × 1 | = 16 |
| Total days | = 1383136 |
Calculating the Tzolkʼin date portion
The Tzolkʼin date is counted forward from 4 Ajaw. To calculate the numerical portion of the Tzolkʼin date, add 4 to the total number of days given by the date and then divide total number of days by 13.
- (4 + 1,383,136) / 13 = 106,395 (and 5/13)
This means that 106,395 whole 13 day cycles have been completed and the numerical portion of the Tzolkʼin date is 5.
To calculate the day, divide the total number of days in the long count by 20 since there are twenty day names.
- 1,383,136 / 20 = 69,156 (and 16/20)
This means 16 day names must be counted from Ajaw. This gives Kibʼ. Therefore, the Tzolkʼin date is 5 Kibʼ.
Calculating the Haabʼ date portion
The Haabʼ date 8 Kumkʼu is the ninth day of the eighteenth month. There are 17 days to the start of the next year.
Subtract 17 days from the total, to find how many complete Haabʼ years are contained.
- 1,383,136 − 17 = 1,383,119
by 365
- 1,383,119 / 365 = 3,789 and (134/365)
Therefore, 3,789 complete Haabʼ have passed and the remainder 134 is the 135th day in the new Haabʼ, since a remainder of 0 would indicate the first day.
Find which month the day is in. Dividing the remainder 134 by 20, is six complete months and a remainder of 14, indicating the 15th day. So, the date in the Haabʼ lies in the seventh month, which is Yaxkʼin. The fifteenth day of Yaxkʼin is 14, thus the Haabʼ date is 14 Yaxkʼin.
So the date of the long count date 9.12.2.0.16 5 Kibʼ 14 Yaxkʼin is confirmed.
Piktuns and higher orders
There are also four rarely used higher-order periods above the bʼakʼtun: piktun, kalabtun, kʼinchiltun and alautun. All of these words are inventions of Mayanists. Each one consists of 20 of the lesser units.
Many inscriptions give the date of the current creation as a large number of 13s preceding 13.0.0.0.0 4 Ahau 8 Kumkʼu. For example, a Late Classic monument from Coba, Stela 1. The date of creation is expressed as 13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.0.0.0.0, where the units are 13s in the nineteen places larger than the bʼakʼtun. Some authors think that the 13s were symbolic of a completion and did not represent an actual number.
Most inscriptions that use these are in the form of distance dates and Long Reckonings – they give a base date, a distance number that is added or subtracted and the resulting Long Count.
The first example below is from Schele (1987). The second is from Stuart (2005 pp. 60, 77)
Palenque Temple of the Cross, tablet, Schele (1987 p.)
12.19.13.4.0 8 Ajaw 18 Tzek in the prior era
6.14.0 Distance number linking to the "era date"
13.0.0.0.0 4 Ajaw 8 Kumkʼu
Palenque Temple XIX, South Panel G2-H6 Stuart (2005 pp. 60, 77)
12.10.1.13.2 9 Ikʼ 5 Mol (seating of GI in the prior era)
2.8.3.8.0
1.18.5.3.2 9 Ikʼ 15 Keh (rebirth of GI, this date also in Temple of the Cross)
The tablet of the inscriptions contains this inscription:
9.8.9.13.0 8 Ajaw 13 Pop
10.11.10.5.8
1.0.0.0.0.8
The Dresden codex contains another method for writing distance numbers. These are Ring Numbers. Specific dates within the Dresden codex are often given by calculations involving Ring Numbers. Förstemann identified these, but Wilson (1924) later clarified the way in which they operate. Ring Numbers are intervals of days between the Era Base date 4 Ajaw 8 Kumkʼu and an earlier Ring Base date, where the place-holder for the numeral of days in the interval is circled by an image of a tied red band. Added to this earlier Ring Base date is another count of days forward, which Thompson refers to as a Long Round, leading to a final date within the Long Count that is given as an entry date to be used within a specific table in the codex.
Ring number (12) 12.12.17.3.1 13 Imix 9 Wo (7.2.14.19 before (13) 13.0.0.0.0)
distance number (0) 10.13.13.3.2
Long Count 10.6.10.6.3 13 Akʼbal 1 Kankʼin
Ring number (portion of the DN preceding era date) 7.2.14.19
Add Ring number to the ring number date to reach 13.0.0.0.0
Thompson contains a table of typical long reckonings after Satterwaite.
The "Serpent Numbers" in the Dresden codex pp. 61–69 is a table of dates using a base date of 1.18.1.8.0.16 in the prior era (5,482,096 days).
See also
Notes
- The correlation between the Long Count and Western calendars is calculated according to the one used by a majority of Maya researchers, known as the (modified) GMT or Goodman-Martinez-Thompson correlation. An alternate correlation sometimes used puts the starting date two days later. August 11, 3114 BCE is a date in the proleptic Gregorian calendar, which is to September 6, −3113 Julian astronomical.
- Notable in this sequence is the glyph with nine variant forms labeled G by early epigraphers. It has been connected with the cycle of Lords of the Night known from colonial era sources in Central Mexico but alternate explanations have also been offered. See Thompson.
- To clarify, there are Long Count inscriptions which refer to dates earlier than the 1st century BCE, but these were carved much later in a retrospective fashion.
- All extant Maya inscriptions that represent this base date wrote it with a "13" bakʼtuns, not "0". But when using "13.0.0.0.0" as a base date in calculations, the "13" bakʼtuns has the numerical value 0, as if it were written as "0.0.0.0.0". This is easily confused when the "13" bakʼtuns has the actual value 13 in the current baktʼun, as in the Maya date for today: 13.0.12.4.5 (=05:33, Sunday, January 12, 2025 (UTC)).
- According to Thompson "The point from which the moon age is counted is not surely known. The possibilities are disappearance of the old moon, conjunction, or appearance of the new moon ... Beyer (1973a) believed that the calculation was made from the disappearance of the old moon. The latter method of counting (disappearance of the old moon) is still current in some Tzeltal, Chol, and Tzotzil villages in Chiapas ..."
- Various sources place this on other dates, notably on December 23.
- Gregorian, using GMT correlation JDN=584283.
- In 46 BC Julius Caesar adopted the convention of having three years of twelve months of approximately 30 days each to make a year of 365 days and a leap year of 366 days. This made the length of the civil year 365.25 days, close to the length of the solar year of 365.2422 days. This is the Julian calendar. By 1582 there was an appreciable discrepancy between the winter solstice and Christmas and the spring equinox and Easter. Pope Gregory XIII, with the help of Italian astronomer Aloysius Lilius (Luigi Lilio), reformed this system by abolishing the days October 5 through October 14, 1582. This brought the civil and tropical years closer together. He also missed three days every four centuries by decreeing that centuries are only leap years if they are evenly divisible by 400. So for example 1700, 1800 and 1900 are not leap years but 1600 and 2000 are. This is the Gregorian calendar. Astronomical calculations will return a year zero and years before that are negative numbers. This is astronomical dating. Years before 46 BC are calculated as proleptic Julian dates. There is no year zero in historical dating. In historical dating the year 1 BCE is followed by the year 1 CE For example, the year −3113 (astronomical dating) is the same as 3114 BCE (historical dating). Many books about the Maya and many computer programs to do Maya calendar conversions use the Proleptic Gregorian calendar. In this calendar all dates before the start of the Gregorian calendar are revised as if the Gregorian calendar had been in use before its adoption in October 1582. Although this system is popular among Mayanists, it is rarely used by anyone else, so for example, dates converted using this system are useless for the study of Maya Astronomy.
- Astronomical algorithms calculate a day as a decimal number equal to a day and a fraction of a day. The Julian date starts at noon. Astronomical dating has a year 0. In historical dating the year 1 BCE is followed by the year 1 CE. Astronomical years before 0 are written with a negative sign. For example, the year 3114 BCE is the year −3113 astronomical.
- "... we have clear evidence that the current Bakʼtun cycle does not conclude at 13, as the last one did, but advances to 20. In other words, 13.0.0.0.0 will be followed by 14.0.0.0.0, 15.0.0.0.0, and so on to 19.0.0.0.0 . A text at the site of Palenque, Mexico, makes this very plain when it records the completion of 1 Piktun, the next unit above the Bakʼtun, in 4772 CE.
References
- Freidel, Schele & Parker (1993, pp. 59–75).
- Boot, p. 2.
- Graham (1992, p. 331, see Fig. 5 for a line drawing of the monument)
- ^ Malmström, Vincent Herschel (1997). "Chapter 6". Cycles of the Sun, Mysteries of the Moon. University of Texas Press. ISBN 978-0-292-75197-2. Archived from the original on 24 August 2011. Retrieved 22 August 2010. Note: Malmström's Gregorian dates are three or four days later than a correlation of 584283 would give (the Misplaced Pages table has been corrected).
- "Vincent H. Mahlstrom". Department of Geography, Faculty & Staff. Dartmouth College. Retrieved 17 February 2014.
- ^ Marcus, Joyce (1976). "The origins of Mesoamerican writing" (PDF). Annual Review of Anthropology. 5. Annual Reviews Inc.: 49–54. doi:10.1146/annurev.an.05.100176.000343.
- ^ Riese, Berthold (1988). "Epigraphy of the southeast zone in relation to other parts of the Maya realm". In Boone, Elizabeth Hill; Willey, Gordon Randolph (eds.). The Southeast Classic Maya Zone: Papers from the Dumbarton Oaks Symposium, 6th and 7th October, 1984. Washington, D.C.: Dumbarton Oaks, Trustees for Harvard University. p. 68. ISBN 978-0-88402-170-4.
- Mora-Marín, David F. (2005). "Kaminaljuyu stela 10: Script classification and linguistic affiliation". Ancient Mesoamerica. 16 (1). Cambridge University Press: 63–87. doi:10.1017/S0956536105050029. ISSN 0956-5361. S2CID 162510333.
The parallel *oo Ͼ *uu Ͼ *u shift in Chʼolan is attested indirectly in the use of the T548 TUN/ HABʼ logogram with the Initial Series Introductory Glyph on Takalik Abaj Stela 2 (236–19 b.c.; Justeson and Mathews 1983; MoraMarín 2001:253).
- ^ Stuart, David (2004). "Chapter 11: The beginnings of the Copan dynasty: A review of the hieroglyphic and historical evidence". In Bell, Ellen E.; Canuto, Marcello A.; Sharer, Robert J. (eds.). Understanding Early Classic Copan. Philadelphia, PA: University of Pennsylvania Museum of Archaeology. p. 219. ISBN 978-1-931707-51-0.
- ^ Ochoa, Lorenzo; Lee, Thomas A., eds. (1983). Antropología e historia de los mixe-zoques y mayas (in Spanish). Mexico: Universidad Nacional Autónoma de México, Instituto de Investigaciones Filológicas, Centro de Estudios Mayas. pp. 191, 194. ISBN 978-968-5804-97-4.
- Diehl (2004, p. 186).
- "A sketch of prior documentation of epi-Olmec texts", Section 5 in Peréz de Lara & Justeson (2005).
- Coe & Koontz (2002), p. 87
- Saturno et al. 2006
- Giron-Abrego 2012
- Thompson, J. Eric. "Maya chronology: The correlation question" (PDF). mesoweb.com. Retrieved 6 September 2015.
- Thompson, J.E.S. Maya hieroglyphic writing. Forgotten Books. p. 73. ISBN 978-1-60506-860-2.
- "Clarifications: The Correlation Debate". alignment2012.com. Retrieved 6 September 2015.
- "Maya Calendar: The Correlation Problem". hermetic.ch. Retrieved 6 September 2015.
- "FAMSI – FAQ's about 2012: The end of the World? – FAQ's – What is this correlation constant?". famsi.org. Retrieved 6 September 2015.
- Breaking the Maya Code, 1992, p. 114.
- Bricker, Harvey M.; Bricker, Victoria Reifler (1 August 2011). Astronomy in the Maya Codices. Memoirs of the American Philosophical Society. American Philosophical Society. p. 85. ISBN 978-0871692658.
if the 12 tun endings in the Chronicle of Oxkutzcab are accepted as referring to the 12 consecutive years and if the calendar-round dates (except that containing the month of Ceh) are correct when translated to a common calendar, the "11.16" correlation is the only possible one.
- The Book of Chilam Balam of Chumayel Ralph L. Roys, Washington D.C.; Carnegie Institution 1933, pp. 79, 83
- Edmonson, Munro S. (December 1976). "The Mayan Calendar Reform of 11.16.0.0.0". Current Anthropology. 17 (4): 713–17. doi:10.1086/201806. JSTOR 2741269. S2CID 145181714.
- Recinos 1953, p. 33 Recinos gives 2 Tihax (Etzʼnabʼ) is September 10, 1541(Julian). The date which marked the destruction of the city of Guatemala founded at the foot of the Volcano of Agua. "After a period of heavy rain there was an earthquake and then a flood of water (a lahar) that destroyed the old city of Guatemala".
- Weeks, John M.; Sachse, Frauke; Prager, Christian M. (15 May 2013). Maya Daykeeping: Three Calendars from Highland Guatemala (Mesoamerican Worlds). University Press of Colorado. pp. 176–84. ISBN 978-1607322467. In Appendix 2, Notes on the Correlation of Maya and Gregorian Calendars, the authors give the examples of December 9, 1722 = 8 Kej 20 Ukabʼ Siʼj (8 Manikʼ 0 Yax) and December 9, 1723 = 9 E 20 Ukabʼ Siʼj (9 Ebʼ 0 Yax). "Using Thompson's correlation constant of A = 584,283, all values from the calendar round correspond with the information in the 1722 Kʼicheʼ calendar."
- (Díaz 1904: 2:129)
- (Sahagún 1975: 12:122)
- Miles, Susanna W, "An Analysis of the Modern Middle American Calendars: A Study in Conservation." In Acculturation in the Americas. Edited by Sol Tax, p. 273. Chicago: University of Chicago Press, 1952.
- Barbara Tedlock, Time and the Highland Maya Revised edition (1992 p. 1)
- Edmonson, Munro S. (1988). The Book of the Year Middle American Calendrical Systems. Salt Lake City: University of Utah Press. ISBN 0-87480-288-1.
- "Lunar Glyphs in the Maya Calendrics – The Lunar Series – The Supplementary and Lunar Glyphs". astras-stargate.com. Retrieved 6 September 2015.
- Fuls (2007) Ancient Mesoamerica, 18, 273–282 Cambridge University Press. after Robertson 1991: Vol. 4 : p. 95.
- Finley, Michael John. "The Dresden Codex eclipse table". Retrieved 1 January 2018.
- Thompson, J. Eric S. (1950). Maya Hieroglyphic Writing, an Introduction. p. 236
- Aveni 2001
- "Sighting the Crescent Moon", Sky & Telescope, July 1994, 14
- "In Quest of the Youngest Moon", Sky & Telescope, December 1996, 104–105
- "Young Moons and the Islamic Calendar", Sky & Telescope, December 1996, 106
- "Seeking Thin Crescent Moons", Sky & Telescope, February 2004, 102–106
- "Young-Moon Hunting in 2005", Sky and Telescope, February 2005, 75–76
- "What's the Thinnest Crescent Moon You Can See?". Sky and Telescope. 13 December 2017.
- Stray, G. (2007). The Mayan and Other Ancient Calendars. Walker. p. 40. ISBN 978-0-8027-1634-7.
- Andreas Fuls (2007). Ancient Mesoamerica, 18, 273–282 Cambridge University Press.
- Bricker and Bricker pp. 249–366
- Bricker and Bricker pp. 163–248
- Ralph, Elizabeth K. (1965). "Review of radiocarbon dates from Tikal and the Maya calendar correlation problem". American Antiquity. 30 (4): 421–427. doi:10.2307/277941. JSTOR 277941. S2CID 163676704.
- Kennett, Douglas J.; Hajdas, Irka; Culleton, Brendan J.; Belmecheri, Soumaya; Martin, Simon; Neff, Hector; et al. (11 April 2013). "Correlating the ancient Maya and modern European calendars with high-precision AMS 14C dating". Scientific Reports. 3: 1597. Bibcode:2013NatSR...3.1597K. doi:10.1038/srep01597. PMC 3623374. PMID 23579869.
- Kennett, Douglas J., et al., "Correlating the ancient Maya and modern European calendars with high-precision AMS 14C dating", Scientific reports 3.1, 2013
- A Derivation of the Maya-to-Julian Calendar Correlation From the Dresden Codex Venus Chronology, in The Sky In Mayan Literature (1992)
- Fuls, Andreas. "The Correlation Question". archaeoastronomie.de. Retrieved 6 September 2015.
- Vladimir Böhm; Bohumil Böhm. "Mayan Dating". hermetic.ch. Retrieved 6 September 2015.
- "Mayan dating, Mayan astronomy, Correlation MD/JD". volny.cz. Retrieved 6 September 2015.
- Stock, Anton. "Dating the eclipse table of the Dresden Codex and the correlation problem". baktun.de. Retrieved 6 September 2015.
- Schele & Freidel (1990), pp. 429–30
- Schele and Friedel (1992).
- "Notes on a New Text from La Corona". decipherment.wordpress.com. Maya Decipherment. 30 June 2012. Retrieved 6 September 2015.
- ^ Schele (1992, pp. 93–95)
- Schele & Freidel (1990, p. 430 n.39)
- ^ MacDonald, G. Jeffrey (27 March 2007). "Does Maya calendar predict 2012 apocalypse?". USA Today. Gannett Company.
- Rivet, Ryan (25 June 2008). "The sky is not falling". New Wave. Tulane University. Archived from the original on 18 April 2011.
- Kettunen, Harri; Helmke, Christophe (2014). "Introduction to Maya Hieroglyphs" (PDF). The Slovak Archaeological and Historical Institute. Wayeb. Bratislava: Comenius University.
- Meeus, Jean (2009) . "Chapter 7: Julian Day". Astronomical Algorithms (Second ed.). Willman-Bell. p. 63. ISBN 978-0-943396-61-3.
with corrections as of 10 August 2009
- Baum, Peter. "Date conversion method". Archived from the original on 10 September 2014.
- Thompson 1960, pp. 314, 316, 148–49 harvnb error: no target: CITEREFThompson1960 (help) Appendix IV: "I have throughout assumed that the baktuns were grouped, not in 13's, but in 20's, for the evidence supporting a vigesimal count of baktuns in Dresden and at Palenque and Copan is too strong to be overridden."
- Grofe, Michael John (2007). The Serpent Series: Precession in the Maya Dresden Codex. p. 55.
On occasion, the Maya also recorded intervals of time even greater than 13 Bʼakʼtuns, such as one Piktun, composed of 20 Bʼakʼtuns. This is relevant to the current discussion concerning the Serpent Series.
- Martin. "Time, Kingship, and the Maya Universe". penn.museum.
- Fig. 444 in Wagner 2006, p. 283 harvnb error: no target: CITEREFWagner2006 (help)
- Schele & Freidel 1992, p. 430 harvnb error: no target: CITEREFScheleFreidel1992 (help)
- D. Freidel; L. Schele; J. Parker (1993). Maya Cosmos: Three Thousand Years On The Shaman's Path. Vol. 62, Fig. 2:1.
- "Schele Drawing Collection". research.famsi.org. Retrieved 6 September 2015.
- ^ Anderson, Lloyd B. (2008). "20 or 13 Baktuns in a Pictun?" (PDF). traditionalhighcultures.org. Archived from the original (PDF) on 14 May 2015. Retrieved 6 September 2015.
- ^ Thompson, J. Eric S. "Distances across Era Date" (PDF). traditionalhighcultures.org. Archived from the original (PDF) on 17 November 2009. Retrieved 13 January 2013. table from Thompson
- Förstemann, Ernst. Commentary on the Maya Manuscript in the Royal Public Library of Dresden. Vol. IV. No. 2. Peabody Museum of American Archaeology and Archaeology and Ethnography, Harvard University. pp. 222–264.
- Thompson 1972, pp. 20–21 harvnb error: no target: CITEREFThompson1972 (help)
- Grofe, Michael John (2007). The Serpent Series: Precession in the Maya Dresden Codex. p. 55.
- Thompson 1972, pp. 20–22 harvnb error: no target: CITEREFThompson1972 (help)
- Beyer, Hermann (1933). "Emendations of the 'Serpent Numbers' of the Dresden Maya Codex". Anthropos (St. Gabriel Mödling bei Wien). 28: 1–7.
- The Long Count Position of the Serpent Number Dates. Vol. I. Mexico: Proc. 27th Int. Cong. Of Amer., Mexico, 1939. 1943. pp. 401–05.
- Grofe, Michael John (2007). The Serpent Series: Precession in the Maya Dresden Codex. p. 63.
Bibliography
- Boot, Eric (2002). "The Dos Pilas-Tikal Wars from the Perspective of Dos Pilas Hieroglyphic Stairway 4" (PDF). Mesoweb. Articles. Retrieved 15 March 2007.
- Bricker, Harvey M.; Bricker, Victoria R. (2011). Astronomy in the Maya Codices. Philadelphia: American Philosophical Society. ISBN 978-0-87169-265-8.
- Coe, Michael D. (1992). Breaking the Maya Code. London and New York: Thames & Hudson. ISBN 0-500-05061-9. OCLC 26605966.
- Coe, Michael D.; Koontz, Rex (2002). Mexico: from the Olmecs to the Aztecs (5th, revised and enlarged ed.). London and New York: Thames & Hudson. ISBN 0-500-28346-X. OCLC 50131575.
- Coe, Michael D.; Van Stone, Mark L (2005). Reading the Maya Glyphs. London: Thames & Hudson. ISBN 978-0-500-28553-4.
- Diehl, Richard (2004). The Olmecs: America's First Civilization. Ancient peoples and places series. London: Thames & Hudson. ISBN 0-500-02119-8. OCLC 56746987.
- Freidel, David; Schele, Linda; Parker, Joy (1993). Maya Cosmos: Three thousand years on the shaman's path. New York: William Morrow. ISBN 0-68810-081-3. OCLC 27430287.
- Giron-Abrego, Mario (2012). "An Early Example of the Logogram TZUTZ at San Bartolo" (PDF). Wayeb. Wayeb Notes. Retrieved 15 March 2013.
- Graham, John A. (1992). J.P. Laporte; H. Escobedo; S. Brady (eds.). "Escultura en bulto Olmeca y Maya en Takʼalik Abʼaj: Su desarrollo y portento" (PDF). IV Simposio de Investigaciones Arqueológicas en Guatemala, 1990 (in Spanish). Guatemala: Museo Nacional de Arqueología y Etnología: 325–334. Archived from the original (PDF) on 11 December 2009. Retrieved 16 March 2013.
- Gronemeyer, Sven (2006). "Glyphs G and F: Identified as aspects of the Maize God" (PDF). Wayeb Notes. 22: 1–23. ISSN 1379-8286. Retrieved 4 April 2007.
- Kelley, David H. (2005). Exploring Ancient Skies: an Encyclopedic Survey of Archaeoastronomy. Berlin: Springer Verlag. ISBN 0-387-95310-8.
- Kelley, David H. (2008). "Archaeoastronomy". In Deborah M. Pearsall (ed.). Encyclopedia of Archaeology, Vol. 1: A. Oxford: Academic Press. pp. 451–64. ISBN 978-0-12-548030-7. OCLC 2007931569.
- MacDonald, G. Jeffrey (27 March 2007). "Does Maya calendar predict 2012 apocalypse?" (online edition). USA Today. McLean, VA: Gannett Company. p. 11D. ISSN 0734-7456. Retrieved 28 May 2009.
- Pérez de Lara, Jorge; Justeson, John (2005). "Photographic Documentation of Monuments with Epi-Olmec Script/Imagery". The Foundation Granting Department: Reports Submitted to FAMSI. Foundation for the Advancement of Mesoamerican Studies, Inc. (FAMSI). Retrieved 4 April 2007.
- Recinos, Adrián (1953). The Annals of the Cakchiquels Translated from the Cakchiquel Maya by Adrián Recinos and Delia Goetz. Translated by Goetz, Delia (1st ed.). Norman: University of Oklahoma Press. pp. 3–165.
- Saturno, William A.; Stuart, David; Beltran, Boris (2006). "Early Maya Writing at San Bartolo, Guatemala". Science. 311 (5765): 1281–1283. Bibcode:2006Sci...311.1281S. doi:10.1126/science.1121745. PMID 16400112. S2CID 46351994.
- Schele, Linda (1992). "A New Look at the Dynastic History of Palenque". In Victoria R. Bricker (Volume), with Patricia A. Andrews (ed.). Supplement to the Handbook of Middle American Indians, Vol. 5: Epigraphy. Victoria Reifler Bricker (general editor). Austin: University of Texas Press. pp. 82–109. ISBN 0-292-77650-0. OCLC 23693597.
- Schele, Linda; Freidel, David (1990). A Forest of Kings: The Untold Story of the Ancient Maya (pbk reprint of 1990 ed.). New York: Harper Perennial. ISBN 0-688-11204-8. OCLC 145324300.
- Thompson, J. Eric S. (1929). "Maya Chronology: Glyph G of the Lunar Series". American Anthropologist. New Series. 31 (2): 223–231. doi:10.1525/aa.1929.31.2.02a00010. ISSN 0002-7294. OCLC 51205515.
- Thompson, J. Eric S. (1971). Maya Hieroglyphic Writing, an Introduction (3rd ed.). Norman, OK: University of Oklahoma Press. ISBN 978-0-8061-0447-8.
- van Stone, Mark L. (2010). 2012: Science and Prophecy of the Ancient Maya. California: Tlacaelel Press. ISBN 978-0-9826826-0-9.
- Voss, Alexander W.; Kremer, H. Juergen (2000). "Kʼakʼ-u-pakal, Hun-pik-tokʼ and the Kokom: The Political Organisation of Chichen Itza" (PDF). 3rd European Maya Conference (1998). Retrieved 26 October 2005.
- Wagner, Elizabeth (2006). "Maya Creation Myths and Cosmology". In Nikolai Grube (ed.). Maya: Divine Kings of the Rain Forest. Eva Eggebrecht and Matthias Seidel (assistant eds.). Cologne: Könemann. pp. 280–293. ISBN 3-8331-1957-8. OCLC 71165439.
External links
- Coba Stela 1 (Schele #4087), partial illustration from the Linda Schele Drawings Collection of the monument from Coba with an expanded Long Count date
- Maya calendar on michielb.nl, with conversion applet from Gregorian calendar to Maya date (Uses the proleptic Gregorian calendar.)
- The Dresden Codex Lunar Series and Sidereal Astronomy
- Day Symbols of the Maya Year at Project Gutenberg 1897 text by Cyrus Thomas.
| Calendars | |||||||
|---|---|---|---|---|---|---|---|
| Systems | |||||||
| In wide use | |||||||
| In more limited use |
| ||||||
| Historical | |||||||
| By specialty |
| ||||||
| Reform proposals | |||||||
| Displays and applications | |||||||
| Year naming and numbering |
| ||||||
| Fictional | |||||||