
In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.
Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points. The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its dual problem of intersecting half-spaces, are fundamental problems of computational geometry. They can be solved in time for two or three dimensional point sets, and in time matching the worst-case output complexity given by the upper bound theorem in higher dimensions.
As well as for finite point sets, convex hulls have also been studied for simple polygons, Brownian motion, space curves, and epigraphs of functions. Convex hulls have wide applications in mathematics, statistics, combinatorial optimization, economics, geometric modeling, and ethology. Related structures include the orthogonal convex hull, convex layers, Delaunay triangulation and Voronoi diagram, and convex skull.
Definitions

A set of points in a Euclidean space is defined to be convex if it contains the line segments connecting each pair of its points. The convex hull of a given set may be defined as
- The (unique) minimal convex set containing
- The intersection of all convex sets containing
- The set of all convex combinations of points in
- The union of all simplices with vertices in
For bounded sets in the Euclidean plane, not all on one line, the boundary of the convex hull is the simple closed curve with minimum perimeter containing . One may imagine stretching a rubber band so that it surrounds the entire set and then releasing it, allowing it to contract; when it becomes taut, it encloses the convex hull of . This formulation does not immediately generalize to higher dimensions: for a finite set of points in three-dimensional space, a neighborhood of a spanning tree of the points encloses them with arbitrarily small surface area, smaller than the surface area of the convex hull. However, in higher dimensions, variants of the obstacle problem of finding a minimum-energy surface above a given shape can have the convex hull as their solution.
For objects in three dimensions, the first definition states that the convex hull is the smallest possible convex bounding volume of the objects. The definition using intersections of convex sets may be extended to non-Euclidean geometry, and the definition using convex combinations may be extended from Euclidean spaces to arbitrary real vector spaces or affine spaces; convex hulls may also be generalized in a more abstract way, to oriented matroids.
Equivalence of definitions

It is not obvious that the first definition makes sense: why should there exist a unique minimal convex set containing , for every ? However, the second definition, the intersection of all convex sets containing , is well-defined. It is a subset of every other convex set that contains , because is included among the sets being intersected. Thus, it is exactly the unique minimal convex set containing . Therefore, the first two definitions are equivalent.
Each convex set containing must (by the assumption that it is convex) contain all convex combinations of points in , so the set of all convex combinations is contained in the intersection of all convex sets containing . Conversely, the set of all convex combinations is itself a convex set containing , so it also contains the intersection of all convex sets containing , and therefore the second and third definitions are equivalent.
In fact, according to Carathéodory's theorem, if is a subset of a -dimensional Euclidean space, every convex combination of finitely many points from is also a convex combination of at most points in . The set of convex combinations of a -tuple of points is a simplex; in the plane it is a triangle and in three-dimensional space it is a tetrahedron. Therefore, every convex combination of points of belongs to a simplex whose vertices belong to , and the third and fourth definitions are equivalent.
Upper and lower hulls
In two dimensions, the convex hull is sometimes partitioned into two parts, the upper hull and the lower hull, stretching between the leftmost and rightmost points of the hull. More generally, for convex hulls in any dimension, one can partition the boundary of the hull into upward-facing points (points for which an upward ray is disjoint from the hull), downward-facing points, and extreme points. For three-dimensional hulls, the upward-facing and downward-facing parts of the boundary form topological disks.
Topological properties
Closed and open hulls
The closed convex hull of a set is the closure of the convex hull, and the open convex hull is the interior (or in some sources the relative interior) of the convex hull.
The closed convex hull of is the intersection of all closed half-spaces containing . If the convex hull of is already a closed set itself (as happens, for instance, if is a finite set or more generally a compact set), then it equals the closed convex hull. However, an intersection of closed half-spaces is itself closed, so when a convex hull is not closed it cannot be represented in this way.
If the open convex hull of a set is -dimensional, then every point of the hull belongs to an open convex hull of at most points of . The sets of vertices of a square, regular octahedron, or higher-dimensional cross-polytope provide examples where exactly points are needed.
Preservation of topological properties

Topologically, the convex hull of an open set is always itself open, and the convex hull of a compact set is always itself compact. However, there exist closed sets for which the convex hull is not closed. For instance, the closed set
(the set of points that lie on or above the witch of Agnesi) has the open upper half-plane as its convex hull.
The compactness of convex hulls of compact sets, in finite-dimensional Euclidean spaces, is generalized by the Krein–Smulian theorem, according to which the closed convex hull of a weakly compact subset of a Banach space (a subset that is compact under the weak topology) is weakly compact.
Extreme points
Main article: Krein–Milman theoremAn extreme point of a convex set is a point in the set that does not lie on any open line segment between any other two points of the same set. For a convex hull, every extreme point must be part of the given set, because otherwise it cannot be formed as a convex combination of given points. According to the Krein–Milman theorem, every compact convex set in a Euclidean space (or more generally in a locally convex topological vector space) is the convex hull of its extreme points. However, this may not be true for convex sets that are not compact; for instance, the whole Euclidean plane and the open unit ball are both convex, but neither one has any extreme points. Choquet theory extends this theory from finite convex combinations of extreme points to infinite combinations (integrals) in more general spaces.
Geometric and algebraic properties
Closure operator
The convex-hull operator has the characteristic properties of a closure operator:
- It is extensive, meaning that the convex hull of every set is a superset of .
- It is non-decreasing, meaning that, for every two sets and with , the convex hull of is a subset of the convex hull of .
- It is idempotent, meaning that for every , the convex hull of the convex hull of is the same as the convex hull of .
When applied to a finite set of points, this is the closure operator of an antimatroid, the shelling antimatroid of the point set. Every antimatroid can be represented in this way by convex hulls of points in a Euclidean space of high-enough dimension.
Minkowski sum
The operations of constructing the convex hull and taking the Minkowski sum commute with each other, in the sense that the Minkowski sum of convex hulls of sets gives the same result as the convex hull of the Minkowski sum of the same sets. This provides a step towards the Shapley–Folkman theorem bounding the distance of a Minkowski sum from its convex hull.
Projective duality
The projective dual operation to constructing the convex hull of a set of points is constructing the intersection of a family of closed halfspaces that all contain the origin (or any other designated point).
Special cases
Finite point sets

The convex hull of a finite point set forms a convex polygon when , or more generally a convex polytope in . Each extreme point of the hull is called a vertex, and (by the Krein–Milman theorem) every convex polytope is the convex hull of its vertices. It is the unique convex polytope whose vertices belong to and that encloses all of . For sets of points in general position, the convex hull is a simplicial polytope.
According to the upper bound theorem, the number of faces of the convex hull of points in -dimensional Euclidean space is . In particular, in two and three dimensions the number of faces is at most linear in .
Simple polygons
Main article: Convex hull of a simple polygon
The convex hull of a simple polygon encloses the given polygon and is partitioned by it into regions, one of which is the polygon itself. The other regions, bounded by a polygonal chain of the polygon and a single convex hull edge, are called pockets. Computing the same decomposition recursively for each pocket forms a hierarchical description of a given polygon called its convex differences tree. Reflecting a pocket across its convex hull edge expands the given simple polygon into a polygon with the same perimeter and larger area, and the Erdős–Nagy theorem states that this expansion process eventually terminates.
Brownian motion
The curve generated by Brownian motion in the plane, at any fixed time, has probability 1 of having a convex hull whose boundary forms a continuously differentiable curve. However, for any angle in the range , there will be times during the Brownian motion where the moving particle touches the boundary of the convex hull at a point of angle . The Hausdorff dimension of this set of exceptional times is (with high probability) .
Space curves

For the convex hull of a space curve or finite set of space curves in general position in three-dimensional space, the parts of the boundary away from the curves are developable and ruled surfaces. Examples include the oloid, the convex hull of two circles in perpendicular planes, each passing through the other's center, the sphericon, the convex hull of two semicircles in perpendicular planes with a common center, and D-forms, the convex shapes obtained from Alexandrov's uniqueness theorem for a surface formed by gluing together two planar convex sets of equal perimeter.
Functions
Main article: Lower convex envelopeThe convex hull or lower convex envelope of a function on a real vector space is the function whose epigraph is the lower convex hull of the epigraph of . It is the unique maximal convex function majorized by . The definition can be extended to the convex hull of a set of functions (obtained from the convex hull of the union of their epigraphs, or equivalently from their pointwise minimum) and, in this form, is dual to the convex conjugate operation.
Computation
Main article: Convex hull algorithmsIn computational geometry, a number of algorithms are known for computing the convex hull for a finite set of points and for other geometric objects. Computing the convex hull means constructing an unambiguous, efficient representation of the required convex shape. Output representations that have been considered for convex hulls of point sets include a list of linear inequalities describing the facets of the hull, an undirected graph of facets and their adjacencies, or the full face lattice of the hull. In two dimensions, it may suffice more simply to list the points that are vertices, in their cyclic order around the hull.
For convex hulls in two or three dimensions, the complexity of the corresponding algorithms is usually estimated in terms of , the number of input points, and , the number of points on the convex hull, which may be significantly smaller than . For higher-dimensional hulls, the number of faces of other dimensions may also come into the analysis. Graham scan can compute the convex hull of points in the plane in time . For points in two and three dimensions, more complicated output-sensitive algorithms are known that compute the convex hull in time . These include Chan's algorithm and the Kirkpatrick–Seidel algorithm. For dimensions , the time for computing the convex hull is , matching the worst-case output complexity of the problem. The convex hull of a simple polygon in the plane can be constructed in linear time.
Dynamic convex hull data structures can be used to keep track of the convex hull of a set of points undergoing insertions and deletions of points, and kinetic convex hull structures can keep track of the convex hull for points moving continuously. The construction of convex hulls also serves as a tool, a building block for a number of other computational-geometric algorithms such as the rotating calipers method for computing the width and diameter of a point set.
Related structures
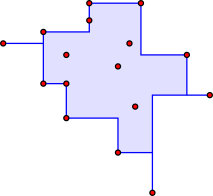 Orthogonal convex hull
Orthogonal convex hull Relative convex hull
Relative convex hull
Several other shapes can be defined from a set of points in a similar way to the convex hull, as the minimal superset with some property, the intersection of all shapes containing the points from a given family of shapes, or the union of all combinations of points for a certain type of combination. For instance:
- The affine hull is the smallest affine subspace of a Euclidean space containing a given set, or the union of all affine combinations of points in the set.
- The linear hull is the smallest linear subspace of a vector space containing a given set, or the union of all linear combinations of points in the set.
- The conical hull or positive hull of a subset of a vector space is the set of all positive combinations of points in the subset.
- The visual hull of a three-dimensional object, with respect to a set of viewpoints, consists of the points such that every ray from a viewpoint through intersects the object. Equivalently it is the intersection of the (non-convex) cones generated by the outline of the object with respect to each viewpoint. It is used in 3D reconstruction as the largest shape that could have the same outlines from the given viewpoints.
- The circular hull or alpha-hull of a subset of the plane is the intersection of all disks with a given radius that contain the subset.
- The relative convex hull of a subset of a two-dimensional simple polygon is the intersection of all relatively convex supersets, where a set within the same polygon is relatively convex if it contains the geodesic between any two of its points.
- The orthogonal convex hull or rectilinear convex hull is the intersection of all orthogonally convex and connected supersets, where a set is orthogonally convex if it contains all axis-parallel segments between pairs of its points.
- The orthogonal convex hull is a special case of a much more general construction, the hyperconvex hull, which can be thought of as the smallest injective metric space containing the points of a given metric space.
- The holomorphically convex hull is a generalization of similar concepts to complex analytic manifolds, obtained as an intersection of sublevel sets of holomorphic functions containing a given set.
The Delaunay triangulation of a point set and its dual, the Voronoi diagram, are mathematically related to convex hulls: the Delaunay triangulation of a point set in can be viewed as the projection of a convex hull in The alpha shapes of a finite point set give a nested family of (non-convex) geometric objects describing the shape of a point set at different levels of detail. Each of alpha shape is the union of some of the features of the Delaunay triangulation, selected by comparing their circumradius to the parameter alpha. The point set itself forms one endpoint of this family of shapes, and its convex hull forms the other endpoint. The convex layers of a point set are a nested family of convex polygons, the outermost of which is the convex hull, with the inner layers constructed recursively from the points that are not vertices of the convex hull.
The convex skull of a polygon is the largest convex polygon contained inside it. It can be found in polynomial time, but the exponent of the algorithm is high.
Applications
Convex hulls have wide applications in many fields. Within mathematics, convex hulls are used to study polynomials, matrix eigenvalues, and unitary elements, and several theorems in discrete geometry involve convex hulls. They are used in robust statistics as the outermost contour of Tukey depth, are part of the bagplot visualization of two-dimensional data, and define risk sets of randomized decision rules. Convex hulls of indicator vectors of solutions to combinatorial problems are central to combinatorial optimization and polyhedral combinatorics. In economics, convex hulls can be used to apply methods of convexity in economics to non-convex markets. In geometric modeling, the convex hull property Bézier curves helps find their crossings, and convex hulls are part of the measurement of boat hulls. And in the study of animal behavior, convex hulls are used in a standard definition of the home range.
Mathematics

Newton polygons of univariate polynomials and Newton polytopes of multivariate polynomials are convex hulls of points derived from the exponents of the terms in the polynomial, and can be used to analyze the asymptotic behavior of the polynomial and the valuations of its roots. Convex hulls and polynomials also come together in the Gauss–Lucas theorem, according to which the roots of the derivative of a polynomial all lie within the convex hull of the roots of the polynomial.
In spectral analysis, the numerical range of a normal matrix is the convex hull of its eigenvalues. The Russo–Dye theorem describes the convex hulls of unitary elements in a C*-algebra. In discrete geometry, both Radon's theorem and Tverberg's theorem concern the existence of partitions of point sets into subsets with intersecting convex hulls.
The definitions of a convex set as containing line segments between its points, and of a convex hull as the intersection of all convex supersets, apply to hyperbolic spaces as well as to Euclidean spaces. However, in hyperbolic space, it is also possible to consider the convex hulls of sets of ideal points, points that do not belong to the hyperbolic space itself but lie on the boundary of a model of that space. The boundaries of convex hulls of ideal points of three-dimensional hyperbolic space are analogous to ruled surfaces in Euclidean space, and their metric properties play an important role in the geometrization conjecture in low-dimensional topology. Hyperbolic convex hulls have also been used as part of the calculation of canonical triangulations of hyperbolic manifolds, and applied to determine the equivalence of knots.
See also the section on Brownian motion for the application of convex hulls to this subject, and the section on space curves for their application to the theory of developable surfaces.
Statistics

In robust statistics, the convex hull provides one of the key components of a bagplot, a method for visualizing the spread of two-dimensional sample points. The contours of Tukey depth form a nested family of convex sets, with the convex hull outermost, and the bagplot also displays another polygon from this nested family, the contour of 50% depth.
In statistical decision theory, the risk set of a randomized decision rule is the convex hull of the risk points of its underlying deterministic decision rules.
Combinatorial optimization
In combinatorial optimization and polyhedral combinatorics, central objects of study are the convex hulls of indicator vectors of solutions to a combinatorial problem. If the facets of these polytopes can be found, describing the polytopes as intersections of halfspaces, then algorithms based on linear programming can be used to find optimal solutions. In multi-objective optimization, a different type of convex hull is also used, the convex hull of the weight vectors of solutions. One can maximize any quasiconvex combination of weights by finding and checking each convex hull vertex, often more efficiently than checking all possible solutions.
Economics
Main article: Convexity in economicsIn the Arrow–Debreu model of general economic equilibrium, agents are assumed to have convex budget sets and convex preferences. These assumptions of convexity in economics can be used to prove the existence of an equilibrium. When actual economic data is non-convex, it can be made convex by taking convex hulls. The Shapley–Folkman theorem can be used to show that, for large markets, this approximation is accurate, and leads to a "quasi-equilibrium" for the original non-convex market.
Geometric modeling
In geometric modeling, one of the key properties of a Bézier curve is that it lies within the convex hull of its control points. This so-called "convex hull property" can be used, for instance, in quickly detecting intersections of these curves.
In the geometry of boat and ship design, chain girth is a measurement of the size of a sailing vessel, defined using the convex hull of a cross-section of the hull of the vessel. It differs from the skin girth, the perimeter of the cross-section itself, except for boats and ships that have a convex hull.
Ethology
The convex hull is commonly known as the minimum convex polygon in ethology, the study of animal behavior, where it is a classic, though perhaps simplistic, approach in estimating an animal's home range based on points where the animal has been observed. Outliers can make the minimum convex polygon excessively large, which has motivated relaxed approaches that contain only a subset of the observations, for instance by choosing one of the convex layers that is close to a target percentage of the samples, or in the local convex hull method by combining convex hulls of neighborhoods of points.
Quantum physics
In quantum physics, the state space of any quantum system — the set of all ways the system can be prepared — is a convex hull whose extreme points are positive-semidefinite operators known as pure states and whose interior points are called mixed states. The Schrödinger–HJW theorem proves that any mixed state can in fact be written as a convex combination of pure states in multiple ways.
Thermodynamics

A convex hull in thermodynamics was identified by Josiah Willard Gibbs (1873), although the paper was published before the convex hull was so named. In a set of energies of several stoichiometries of a material, only those measurements on the lower convex hull will be stable. When removing a point from the hull and then calculating its distance to the hull, its distance to the new hull represents the degree of stability of the phase.
History
The lower convex hull of points in the plane appears, in the form of a Newton polygon, in a letter from Isaac Newton to Henry Oldenburg in 1676. The term "convex hull" itself appears as early as the work of Garrett Birkhoff (1935), and the corresponding term in German appears earlier, for instance in Hans Rademacher's review of Kőnig (1922). Other terms, such as "convex envelope", were also used in this time frame. By 1938, according to Lloyd Dines, the term "convex hull" had become standard; Dines adds that he finds the term unfortunate, because the colloquial meaning of the word "hull" would suggest that it refers to the surface of a shape, whereas the convex hull includes the interior and not just the surface.
Notes
- The terminology convex closure refers to the fact that the convex hull defines a closure operator. However, this term is also frequently used to refer to the closed convex hull, with which it should not be confused — see e.g Fan (1959), p.48.
- ^ Rockafellar (1970), p. 12.
- ^ de Berg et al. (2008), p. 3.
- Williams & Rossignac (2005). See also Douglas Zare, answer to "the perimeter of a non-convex set", MathOverflow, May 16, 2014.
- Oberman (2007).
- Knuth (1992).
- ^ Rockafellar (1970), p. 12; Lay (1982), p. 17.
- de Berg et al. (2008), p. 6. The idea of partitioning the hull into two chains comes from an efficient variant of Graham scan by Andrew (1979).
- Sontag (1982).
- Rockafellar (1970), p. 99.
- Steinitz (1914); Gustin (1947); Bárány, Katchalski & Pach (1982)
- Grünbaum (2003), p. 16; Lay (1982), p. 21; Sakuma (1977).
- This example is given by Talman (1977), Remark 2.6.
- Whitley (1986).
- Krein & Milman (1940); Lay (1982), p. 43.
- Okon (2000).
- Kiselman (2002).
- Kashiwabara, Nakamura & Okamoto (2005).
- Krein & Šmulian (1940), Theorem 3, pages 562–563; Schneider (1993), Theorem 1.1.2 (pages 2–3) and Chapter 3.
- de Berg et al. (2008), p. 254.
- Grünbaum (2003), p. 57.
- de Berg et al. (2008), p. 256.
- de Berg et al. (2008), p. 245.
- Rappoport (1992).
- Demaine et al. (2008).
- Cranston, Hsu & March (1989).
- Sedykh (1981).
- Dirnböck & Stachel (1997).
- Seaton (2017).
- Rockafellar (1970), p. 36.
- Rockafellar (1970), p. 149.
- Avis, Bremner & Seidel (1997).
- de Berg et al. (2008), p. 13.
- Chazelle (1993); de Berg et al. (2008), p. 256.
- McCallum & Avis (1979); Graham & Yao (1983); Lee (1983).
- Chan (2012).
- Basch, Guibas & Hershberger (1999).
- Toussaint (1983).
- ^ Westermann (1976).
- Laurentini (1994).
- ^ Edelsbrunner, Kirkpatrick & Seidel (1983).
- Toussaint (1986).
- Ottmann, Soisalon-Soininen & Wood (1984).
- Herrlich (1992).
- Rossi (1961).
- Brown (1979).
- Chazelle (1985).
- Chang & Yap (1986).
- Artin (1967); Gel'fand, Kapranov & Zelevinsky (1994)
- Prasolov (2004).
- Johnson (1976).
- Gardner (1984).
- Reay (1979).
- Epstein & Marden (1987).
- Weeks (1993).
- Rousseeuw, Ruts & Tukey (1999).
- Harris (1971).
- Pulleyblank (1983); see especially remarks following Theorem 2.9.
- Katoh (1992).
- Nicola (2000). See in particular Section 16.9, Non Convexity and Approximate Equilibrium, pp. 209–210.
- Chen & Wang (2003).
- Mason (1908).
- Kernohan, Gitzen & Millspaugh (2001), p. 137–140; Nilsen, Pedersen & Linnell (2008)
- Worton (1995).
- Getz & Wilmers (2004).
- Rieffel & Polak (2011).
- Kirkpatrick (2006).
- Kim et al. (2019).
- Gibbs (1873).
- Hautier (2014); Fultz (2020)
- Newton (1676); see Auel (2019), page 336, and Escobar & Kaveh (2020).
- See, e.g., White (1923), page 520.
- Dines (1938).
References
- Fan, Ky (1959), Convex Sets and Their Applications. Summer Lectures 1959., Argon national laboratory
- Andrew, A. M. (1979), "Another efficient algorithm for convex hulls in two dimensions", Information Processing Letters, 9 (5): 216–219, doi:10.1016/0020-0190(79)90072-3
- Artin, Emil (1967), "2.5. Newton's Polygon", Algebraic Numbers and Algebraic Functions, Gordon and Breach, pp. 37–43, MR 0237460
- Auel, Asher (2019), "The mathematics of Grace Murray Hopper" (PDF), Notices of the American Mathematical Society, 66 (3): 330–340, doi:10.1090/noti1810, MR 3889348, S2CID 76650751
- Avis, David; Bremner, David; Seidel, Raimund (1997), "How good are convex hull algorithms?", Computational Geometry, 7 (5–6): 265–301, doi:10.1016/S0925-7721(96)00023-5, MR 1447243
- Bárány, Imre; Katchalski, Meir; Pach, János (1982), "Quantitative Helly-type theorems", Proceedings of the American Mathematical Society, 86 (1): 109–114, doi:10.1090/S0002-9939-1982-0663877-X, JSTOR 2044407, MR 0663877
- Basch, Julien; Guibas, Leonidas J.; Hershberger, John (1999), "Data structures for mobile data", Journal of Algorithms, 31 (1): 1–28, CiteSeerX 10.1.1.134.6921, doi:10.1006/jagm.1998.0988, MR 1670903, S2CID 8013433
- Birkhoff, Garrett (1935), "Integration of functions with values in a Banach space", Transactions of the American Mathematical Society, 38 (2): 357–378, doi:10.2307/1989687, JSTOR 1989687, MR 1501815
- Brown, K. Q. (1979), "Voronoi diagrams from convex hulls", Information Processing Letters, 9 (5): 223–228, doi:10.1016/0020-0190(79)90074-7, S2CID 44537056
- de Berg, M.; van Kreveld, M.; Overmars, Mark; Schwarzkopf, O. (2008), Computational Geometry: Algorithms and Applications (3rd ed.), Springer
- Chan, Timothy M. (2012), "Three problems about dynamic convex hulls", International Journal of Computational Geometry and Applications, 22 (4): 341–364, doi:10.1142/S0218195912600096, MR 2994585
- Chang, J. S.; Yap, C.-K. (1986), "A polynomial solution for the potato-peeling problem", Discrete & Computational Geometry, 1 (2): 155–182, doi:10.1007/BF02187692, MR 0834056
- Chazelle, Bernard (1985), "On the convex layers of a planar set", IEEE Transactions on Information Theory, 31 (4): 509–517, doi:10.1109/TIT.1985.1057060, MR 0798557
- Chazelle, Bernard (1993), "An optimal convex hull algorithm in any fixed dimension" (PDF), Discrete & Computational Geometry, 10 (1): 377–409, CiteSeerX 10.1.1.113.8709, doi:10.1007/BF02573985, S2CID 26605267
- Chen, Qinyu; Wang, Guozhao (March 2003), "A class of Bézier-like curves", Computer Aided Geometric Design, 20 (1): 29–39, doi:10.1016/s0167-8396(03)00003-7
- Cranston, M.; Hsu, P.; March, P. (1989), "Smoothness of the convex hull of planar Brownian motion", Annals of Probability, 17 (1): 144–150, doi:10.1214/aop/1176991500, JSTOR 2244202, MR 0972777
- Demaine, Erik D.; Gassend, Blaise; O'Rourke, Joseph; Toussaint, Godfried T. (2008), "All polygons flip finitely ... right?", Surveys on Discrete and Computational Geometry, Contemporary Mathematics, vol. 453, Providence, Rhode Island: American Mathematical Society, pp. 231–255, doi:10.1090/conm/453/08801, ISBN 978-0-8218-4239-3, MR 2405683
- Dines, L. L. (1938), "On convexity", American Mathematical Monthly, 45 (4): 199–209, doi:10.2307/2302604, JSTOR 2302604, MR 1524247
- Dirnböck, Hans; Stachel, Hellmuth (1997), "The development of the oloid" (PDF), Journal for Geometry and Graphics, 1 (2): 105–118, MR 1622664
- Edelsbrunner, Herbert; Kirkpatrick, David G.; Seidel, Raimund (1983), "On the shape of a set of points in the plane", IEEE Transactions on Information Theory, 29 (4): 551–559, doi:10.1109/TIT.1983.1056714
- Epstein, D. B. A.; Marden, A. (1987), "Convex hulls in hyperbolic space, a theorem of Sullivan, and measured pleated surfaces", in Epstein, D. B. A. (ed.), Analytical and geometric aspects of hyperbolic space (Coventry/Durham, 1984), London Mathematical Society Lecture Note Series, vol. 111, Cambridge: Cambridge University Press, pp. 113–253, MR 0903852
- Escobar, Laura; Kaveh, Kiumars (September 2020), "Convex polytopes, algebraic geometry, and combinatorics" (PDF), Notices of the American Mathematical Society, 67 (8): 1116–1123, doi:10.1090/noti2137, S2CID 221659506
- Fultz, Brent (April 2020), Phase Transitions in Materials, Cambridge University Press, p. 55, doi:10.1017/9781108641449, ISBN 9781108641449
- Gardner, L. Terrell (1984), "An elementary proof of the Russo-Dye theorem", Proceedings of the American Mathematical Society, 90 (1): 171, doi:10.2307/2044692, JSTOR 2044692, MR 0722439, S2CID 119501393
- Gel'fand, I. M.; Kapranov, M. M.; Zelevinsky, A. V. (1994), "6. Newton Polytopes and Chow Polytopes", Discriminants, Resultants, and Multidimensional Determinants, Mathematics: Theory & Applications, Birkhäuser, pp. 193–213, doi:10.1007/978-0-8176-4771-1, ISBN 0-8176-3660-9, MR 1264417
- Getz, Wayne M.; Wilmers, Christopher C. (2004), "A local nearest-neighbor convex-hull construction of home ranges and utilization distributions" (PDF), Ecography, 27 (4), Wiley: 489–505, Bibcode:2004Ecogr..27..489G, doi:10.1111/j.0906-7590.2004.03835.x, S2CID 14592779
- Gibbs, Willard J. (1873), "A method of geometrical representation of the thermodynamic properties of substances by means of surfaces", Transactions of the Connecticut Academy of Arts and Sciences, 2: 382–404; reprinted in The Scientific Papers of J. Willard Gibbs, Vol. I: Thermodynamics, Longmans, Green, & Co., 1906, pp. 33–54
- Graham, Ronald L.; Yao, F. Frances (1983), "Finding the convex hull of a simple polygon", Journal of Algorithms, 4 (4): 324–331, doi:10.1016/0196-6774(83)90013-5, MR 0729228
- Grünbaum, Branko (2003), Convex Polytopes, Graduate Texts in Mathematics, vol. 221 (2nd ed.), Springer, ISBN 9780387004242
- Gustin, William (1947), "On the interior of the convex hull of a Euclidean set", Bulletin of the American Mathematical Society, 53 (4): 299–301, doi:10.1090/S0002-9904-1947-08787-5, MR 0020800
- Harris, Bernard (1971), "Mathematical models for statistical decision theory" (PDF), Optimizing methods in statistics (Proc. Sympos., Ohio State Univ., Columbus, Ohio, 1971), pp. 369–389, MR 0356305, archived from the original (PDF) on 2021-02-28, retrieved 2020-01-01
- Hautier, Geoffroy (2014), "Data mining approaches to high-throughput crystal structure and compound prediction", in Atahan-Evrenk, Sule; Aspuru-Guzik, Alan (eds.), Prediction and Calculation of Crystal Structures: Methods and Applications, Topics in Current Chemistry, vol. 345, Springer International Publishing, pp. 139–179, doi:10.1007/128_2013_486, ISBN 978-3-319-05773-6, PMID 24287952; see p. 143
- Herrlich, Horst (1992), "Hyperconvex hulls of metric spaces", Proceedings of the Symposium on General Topology and Applications (Oxford, 1989), Topology and Its Applications, 44 (1–3): 181–187, doi:10.1016/0166-8641(92)90092-E, MR 1173256
- Johnson, Charles R. (1976), "Normality and the numerical range", Linear Algebra and Its Applications, 15 (1): 89–94, doi:10.1016/0024-3795(76)90080-x, MR 0460358
- Kashiwabara, Kenji; Nakamura, Masataka; Okamoto, Yoshio (2005), "The affine representation theorem for abstract convex geometries", Computational Geometry, 30 (2): 129–144, CiteSeerX 10.1.1.14.4965, doi:10.1016/j.comgeo.2004.05.001, MR 2107032
- Katoh, Naoki (1992), "Bicriteria network optimization problems", IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, E75-A: 321–329
- Kernohan, Brian J.; Gitzen, Robert A.; Millspaugh, Joshua J. (2001), "Analysis of animal space use and movements", in Millspaugh, Joshua; Marzluff, John M. (eds.), Radio Tracking and Animal Populations, Academic Press, ISBN 9780080540221
- Kim, Sooran; Kim, Kyoo; Koo, Jahyun; Lee, Hoonkyung; Min, Byung Il; Kim, Duck Young (December 2019), "Pressure-induced phase transitions and superconductivity in magnesium carbides", Scientific Reports, 9 (1): 20253, Bibcode:2019NatSR...920253K, doi:10.1038/s41598-019-56497-6, PMC 6934831, PMID 31882982
- Kirkpatrick, K. A. (2006), "The Schrödinger–HJW theorem", Foundations of Physics Letters, 19 (1): 95–102, arXiv:quant-ph/0305068, Bibcode:2006FoPhL..19...95K, doi:10.1007/s10702-006-1852-1, S2CID 15995449
- Kiselman, Christer O. (2002), "A semigroup of operators in convexity theory", Transactions of the American Mathematical Society, 354 (5): 2035–2053, doi:10.1090/S0002-9947-02-02915-X, MR 1881029
- Knuth, Donald E. (1992), Axioms and Hulls, Lecture Notes in Computer Science, vol. 606, Heidelberg: Springer-Verlag, doi:10.1007/3-540-55611-7, ISBN 3-540-55611-7, MR 1226891, S2CID 5452191, archived from the original on 2017-06-20, retrieved 2011-09-15
- Kőnig, Dénes (December 1922), "Über konvexe Körper", Mathematische Zeitschrift, 14 (1): 208–210, doi:10.1007/bf01215899, S2CID 128041360; see also review by Hans Rademacher (1922), JFM 48.0835.01
- Krein, Mark; Milman, David (1940), "On extreme points of regular convex sets", Studia Mathematica, 9: 133–138, doi:10.4064/sm-9-1-133-138
- Krein, M.; Šmulian, V. (1940), "On regularly convex sets in the space conjugate to a Banach space", Annals of Mathematics, Second Series, 41 (3): 556–583, doi:10.2307/1968735, hdl:10338.dmlcz/100106, JSTOR 1968735, MR 0002009
- Laurentini, A. (1994), "The visual hull concept for silhouette-based image understanding", IEEE Transactions on Pattern Analysis and Machine Intelligence, 16 (2): 150–162, doi:10.1109/34.273735
- Lay, Steven R. (1982), Convex Sets and their Applications, John Wiley & Sons, ISBN 0-471-09584-2, MR 0655598
- Lee, D. T. (1983), "On finding the convex hull of a simple polygon", International Journal of Computer and Information Sciences, 12 (2): 87–98, doi:10.1007/BF00993195, MR 0724699, S2CID 28600832
- Mason, Herbert B. (1908), Encyclopaedia of Ships and Shipping, p. 698
- McCallum, Duncan; Avis, David (1979), "A linear algorithm for finding the convex hull of a simple polygon", Information Processing Letters, 9 (5): 201–206, doi:10.1016/0020-0190(79)90069-3, MR 0552534
- Newton, Isaac (October 24, 1676), "Letter to Henry Oldenburg", The Newton Project, University of Oxford
- Nicola, Piercarlo (2000), "General Competitive Equilibrium", Mainstream Mathematical Economics in the 20th Century, Springer, pp. 197–215, doi:10.1007/978-3-662-04238-0_16, ISBN 978-3-642-08638-0
- Nilsen, Erlend B.; Pedersen, Simen; Linnell, John D. C. (2008), "Can minimum convex polygon home ranges be used to draw biologically meaningful conclusions?", Ecological Research, 23 (3): 635–639, Bibcode:2008EcoR...23..635N, doi:10.1007/s11284-007-0421-9, S2CID 30843551
- Oberman, Adam M. (2007), "The convex envelope is the solution of a nonlinear obstacle problem", Proceedings of the American Mathematical Society, 135 (6): 1689–1694, doi:10.1090/S0002-9939-07-08887-9, MR 2286077
- Okon, T. (2000), "Choquet theory in metric spaces", Zeitschrift für Analysis und ihre Anwendungen, 19 (2): 303–314, doi:10.4171/ZAA/952, MR 1768994
- Ottmann, T.; Soisalon-Soininen, E.; Wood, Derick (1984), "On the definition and computation of rectilinear convex hulls", Information Sciences, 33 (3): 157–171, doi:10.1016/0020-0255(84)90025-2
- Prasolov, Victor V. (2004), "1.2.1 The Gauss–Lucas theorem", Polynomials, Algorithms and Computation in Mathematics, vol. 11, Springer, pp. 12–13, doi:10.1007/978-3-642-03980-5, ISBN 3-540-40714-6, MR 2082772
- Pulleyblank, W. R. (1983), "Polyhedral combinatorics", in Bachem, Achim; Korte, Bernhard; Grötschel, Martin (eds.), Mathematical Programming: The State of the Art (XIth International Symposium on Mathematical Programming, Bonn 1982), Springer, pp. 312–345, doi:10.1007/978-3-642-68874-4_13, ISBN 978-3-642-68876-8
- Rappoport, Ari (1992), "An efficient adaptive algorithm for constructing the convex differences tree of a simple polygon", Computer Graphics Forum, 11 (4): 235–240, doi:10.1111/1467-8659.1140235, S2CID 20137707
- Reay, John R. (1979), "Several generalizations of Tverberg's theorem", Israel Journal of Mathematics, 34 (3): 238–244 (1980), doi:10.1007/BF02760885, MR 0570883, S2CID 121352925
- Rieffel, Eleanor G.; Polak, Wolfgang H. (2011), Quantum Computing: A Gentle Introduction, MIT Press, pp. 215–216, ISBN 978-0-262-01506-6
- Rockafellar, R. Tyrrell (1970), Convex Analysis, Princeton Mathematical Series, vol. 28, Princeton, N.J.: Princeton University Press, MR 0274683
- Rossi, Hugo (1961), "Holomorphically convex sets in several complex variables", Annals of Mathematics, Second Series, 74 (3): 470–493, doi:10.2307/1970292, JSTOR 1970292, MR 0133479
- Rousseeuw, Peter J.; Ruts, Ida; Tukey, John W. (1999), "The bagplot: A bivariate boxplot", The American Statistician, 53 (4): 382–387, doi:10.1080/00031305.1999.10474494
- Sakuma, Itsuo (1977), "Closedness of convex hulls", Journal of Economic Theory, 14 (1): 223–227, doi:10.1016/0022-0531(77)90095-3
- Schneider, Rolf (1993), Convex Bodies: The Brunn–Minkowski Theory, Encyclopedia of Mathematics and its Applications, vol. 44, Cambridge: Cambridge University Press, doi:10.1017/CBO9780511526282, ISBN 0-521-35220-7, MR 1216521
- Seaton, Katherine A. (2017), "Sphericons and D-forms: a crocheted connection", Journal of Mathematics and the Arts, 11 (4): 187–202, arXiv:1603.08409, doi:10.1080/17513472.2017.1318512, MR 3765242, S2CID 84179479
- Sedykh, V. D. (1981), "Structure of the convex hull of a space curve", Trudy Seminara imeni I. G. Petrovskogo (6): 239–256, MR 0630708, translated in Journal of Soviet Mathematics 33 (4): 1140–1153, 1986, doi:10.1007/BF01086114
- Sontag, Eduardo D. (1982), "Remarks on piecewise-linear algebra", Pacific Journal of Mathematics, 98 (1): 183–201, doi:10.2140/pjm.1982.98.183, MR 0644949, S2CID 18446330
- Steinitz, E. (1914), "Bedingt konvergente Reihen und konvexe Systeme. (Fortsetzung)", Journal für die Reine und Angewandte Mathematik, 1914 (144): 1–40, doi:10.1515/crll.1914.144.1, MR 1580890, S2CID 122998337
- Talman, Louis A. (1977), "Fixed points for condensing multifunctions in metric spaces with convex structure", Kōdai Mathematical Seminar Reports, 29 (1–2): 62–70, MR 0463985
- Toussaint, Godfried (1983), "Solving geometric problems with the rotating calipers", Proceedings of IEEE MELECON '83, Athens, CiteSeerX 10.1.1.155.5671
- Toussaint, Godfried (1986), "An optimal algorithm for computing the relative convex hull of a set of points in a polygon", Proceedings of EURASIP, Signal Processing III: Theories and Applications, Part 2, North-Holland, pp. 853–856
- Weeks, Jeffrey R. (1993), "Convex hulls and isometries of cusped hyperbolic 3-manifolds", Topology and Its Applications, 52 (2): 127–149, doi:10.1016/0166-8641(93)90032-9, MR 1241189
- Westermann, L. R. J. (1976), "On the hull operator", Indagationes Mathematicae, 38 (2): 179–184, doi:10.1016/1385-7258(76)90065-2, MR 0404097
- White, F. Puryer (April 1923), "Pure mathematics", Science Progress in the Twentieth Century, 17 (68): 517–526, JSTOR 43432008
- Whitley, Robert (1986), "The Kreĭn-Šmulian theorem", Proceedings of the American Mathematical Society, 97 (2): 376–377, doi:10.2307/2046536, JSTOR 2046536, MR 0835903
- Williams, Jason; Rossignac, Jarek (2005), "Tightening: curvature-limiting morphological simplification", in Kobbelt, Leif; Shapiro, Vadim (eds.), Proceedings of the Tenth ACM Symposium on Solid and Physical Modeling 2005, Cambridge, Massachusetts, USA, June 13-15, 2005, ACM, pp. 107–112, doi:10.1145/1060244.1060257, hdl:1853/3736, S2CID 15514388
- Worton, Bruce J. (1995), "A convex hull-based estimator of home-range size", Biometrics, 51 (4): 1206–1215, doi:10.2307/2533254, JSTOR 2533254
External links
- "Convex hull", Encyclopedia of Mathematics, EMS Press, 2001
- Weisstein, Eric W., "Convex Hull", MathWorld
- "Convex Hull" by Eric W. Weisstein, Wolfram Demonstrations Project, 2007.
| Convex analysis and variational analysis | |
|---|---|
| Basic concepts | |
| Topics (list) | |
| Maps | |
| Main results (list) | |
| Sets | |
| Series | |
| Duality | |
| Applications and related | |
 for two or three dimensional point sets, and in time matching the worst-case output complexity given by the
for two or three dimensional point sets, and in time matching the worst-case output complexity given by the  may be defined as
may be defined as
 and then releasing it, allowing it to contract; when it becomes taut, it encloses the convex hull of
and then releasing it, allowing it to contract; when it becomes taut, it encloses the convex hull of  that contains
that contains  -dimensional Euclidean space, every convex combination of finitely many points from
-dimensional Euclidean space, every convex combination of finitely many points from  points in
points in  -tuple of points is a
-tuple of points is a  points of
points of 
 , the convex hull of
, the convex hull of  forms a
forms a  , or more generally a
, or more generally a  . Each extreme point of the hull is called a
. Each extreme point of the hull is called a  points in
points in  . In particular, in two and three dimensions the number of faces is at most linear in
. In particular, in two and three dimensions the number of faces is at most linear in  in the range
in the range  , there will be times during the Brownian motion where the moving particle touches the boundary of the convex hull at a point of angle
, there will be times during the Brownian motion where the moving particle touches the boundary of the convex hull at a point of angle  .
.
 on a real vector space is the function whose
on a real vector space is the function whose  , the number of points on the convex hull, which may be significantly smaller than
, the number of points on the convex hull, which may be significantly smaller than  . These include
. These include  , the time for computing the convex hull is
, the time for computing the convex hull is  such that every ray from a viewpoint through
such that every ray from a viewpoint through  that contain the subset.
that contain the subset. can be viewed as the projection of a convex hull in
can be viewed as the projection of a convex hull in  The
The