Multi-stage game - Misplaced Pages

In game theory, a multi-stage game is a sequence of several simultaneous games played one after the other. This is a generalization of a repeated game: a repeated game is a special case of a multi-stage game, in which the stage games are identical.

Multi-Stage Game with Different Information Sets

As an example, consider a two-stage game in which the stage game in Figure 1 is played in each of two periods:

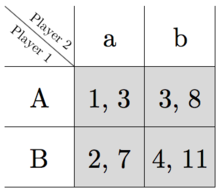
The payoff to each player is the simple sum of the payoffs of both games.

Players cannot observe the action of the other player within a round; however, at the beginning of Round 2, Player 2 finds out about Player 1's action in Round 1, while Player 1 does not find out about Player 2's action in Round 1.

For Player 1, there are ${\textstyle 2^{3}=8}$ strategies.

For Player 2, there are ${\textstyle 2^{5}=32}$ strategies.

The extensive form of this multi-stage game is shown in Figure 2:

In this game, the only Nash Equilibrium in each stage is (B, b).

(BB, bb) will be the Nash Equilibrium for the entire game.

Multi-Stage Game with Changing Payoffs

In this example, consider a two-stage game in which the stage game in Figure 3 is played in the first period and the game in Figure 4 is played in the second:

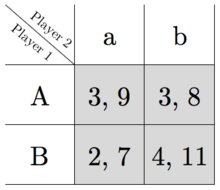
The payoff to each player is the simple sum of the payoffs of both games.

Players cannot observe the action of the other player within a round; however, at the beginning of Round 2, both players find out about the other's action in Round 1.

For Player 1, there are ${\textstyle 2^{5}=32}$ strategies.

For Player 2, there are ${\textstyle 2^{5}=32}$ strategies.

The extensive form of this multi-stage game is shown in Figure 5:

Each of the two stages has two Nash Equilibria: which are (A, a), (B, b), (X, x), and (Y, y).

If the complete contingent strategy of Player 1 matches Player 2 (i.e. AXXXX, axxxx), it will be a Nash Equilibrium. There are 32 such combinations in this multi-stage game. Additionally, all of these equilibria are subgame-perfect.

References

Steve Tadelis. "Multi-Stage Games" (PDF). Retrieved 6 October 2016.

Fudenberg, Drew; Tirole, Jean (1991). Game Theory. Cambridge, Massachusetts: MIT Press. ISBN 9780262061414. Book preview.
Watson, Joel (2013). Strategy: an introduction to game theory (Third ed.). New York. ISBN 978-0-393-91838-0. OCLC 842323069.{{cite book}}: CS1 maint: location missing publisher (link)

This game theory article is a stub. You can help Misplaced Pages by expanding it.

Categories: