
A nested set collection or nested set family is a collection of sets that consists of chains of subsets forming a hierarchical structure, like Russian dolls.
It is used as reference concept in scientific hierarchy definitions, and many technical approaches, like the tree in computational data structures or nested set model of relational databases.
Sometimes the concept is confused with a collection of sets with a hereditary property (like finiteness in a hereditarily finite set).
Formal definition
Some authors regard a nested set collection as a family of sets. Others prefer to classify it relation as an inclusion order.
Let B be a non-empty set and C a collection of subsets of B. Then C is a nested set collection if:
- (and, for some authors, )
The first condition states that the whole set B, which contains all the elements of every subset, must belong to the nested set collection. Some authors do not assume that B is nonempty.
The second condition states that the intersection of every couple of sets in the nested set collection is not the empty set only if one set is a subset of the other.
In particular, when scanning all pairs of subsets at the second condition, it is true for any combination with B.
Example
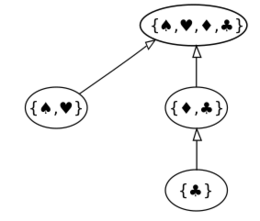
Using a set of atomic elements, as the set of the playing card suits:
- B = {♠, ♥, ♦, ♣}; B1 = {♠, ♥}; B2 = {♦, ♣}; B3 = {♣};
C = {B, B1, B2, B3}.
The second condition of the formal definition can be checked by combining all pairs:
- B1 ∩ B2 = ∅; B1 ∩ B3 = ∅; B3 ⊂ B2.
There is a hierarchy that can be expressed by two branches and its nested order: B3 ⊂ B2 ⊂ B; B1 ⊂ B.
Derived concepts
As sets, that are general abstraction and foundations for many concepts, the nested set is the foundation for "nested hierarchy", "containment hierarchy" and others.
Nested hierarchy
A nested hierarchy or inclusion hierarchy is a hierarchical ordering of nested sets. The concept of nesting is exemplified in Russian matryoshka dolls. Each doll is encompassed by another doll, all the way to the outer doll. The outer doll holds all of the inner dolls, the next outer doll holds all the remaining inner dolls, and so on. Matryoshkas represent a nested hierarchy where each level contains only one object, i.e., there is only one of each size of doll; a generalized nested hierarchy allows for multiple objects within levels but with each object having only one parent at each level. Illustrating the general concept:
A square can always also be referred to as a quadrilateral, polygon or shape. In this way, it is a hierarchy. However, consider the set of polygons using this classification. A square can only be a quadrilateral; it can never be a triangle, hexagon, etc.
Nested hierarchies are the organizational schemes behind taxonomies and systematic classifications. For example, using the original Linnaean taxonomy (the version he laid out in the 10th edition of Systema Naturae), a human can be formulated as:
Taxonomies may change frequently (as seen in biological taxonomy), but the underlying concept of nested hierarchies is always the same.
Containment hierarchy
A containment hierarchy is a direct extrapolation of the nested hierarchy concept. All of the ordered sets are still nested, but every set must be "strict" — no two sets can be identical. The shapes example above can be modified to demonstrate this:
The notation means x is a subset of y but is not equal to y.
Containment hierarchy is used in class inheritance of object-oriented programming.
See also
- Hereditarily countable set
- Hereditary property
- Hierarchy (mathematics)
- Nested set model for storing hierarchical information in relational databases
References
- ^ B. Korte and J. Vygen (2012). Combinatorial Optimization. Springer, Heidelberg.
- "Digital Libraries and Archives: 8th Italian Research Conference, IRCDL 2012 - Bari, Italy, February 9–10, 2012, Revised Selected Papers", edited by Maristella Agosti, Floriana Esposito, Stefano Ferilli, Nicola Ferro. Published in 2013. ISBN 9783642358340. Definition at page 221.
- Lane, David (2006). "Hierarchy, Complexity, Society". In Pumain, Denise (ed.). Hierarchy in Natural and Social Sciences. New York, New York: Springer-Verlag. pp. 81–120. ISBN 978-1-4020-4126-6.
- Linnaei, Carl von (1959). Systema naturae per regna tria naturae :secundum classes, ordines, genera, species, cum characteribus, differentiis, synonymis, locis (in Latin) (10th ed.). Stockholm: Impensis Direct. ISBN 0-665-53008-0. Retrieved 2011-09-24.
| Set theory | ||
|---|---|---|
| Overview |  | |
| Axioms | ||
| Operations |
| |
| ||
| Set types | ||
| Theories | ||
| ||
| Set theorists | ||
 (and, for some authors,
(and, for some authors,  )
)



 means x is a subset of y but is not equal to y.
means x is a subset of y but is not equal to y.