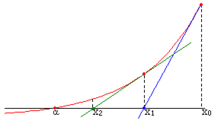
In numerical analysis, the Newton–Raphson method, also known simply as Newton's method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real-valued function. The most basic version starts with a real-valued function f, its derivative f′, and an initial guess x0 for a root of f. If f satisfies certain assumptions and the initial guess is close, then
is a better approximation of the root than x0. Geometrically, (x1, 0) is the x-intercept of the tangent of the graph of f at (x0, f(x0)): that is, the improved guess, x1, is the unique root of the linear approximation of f at the initial guess, x0. The process is repeated as
until a sufficiently precise value is reached. The number of correct digits roughly doubles with each step. This algorithm is first in the class of Householder's methods, and was succeeded by Halley's method. The method can also be extended to complex functions and to systems of equations.
Description
The idea is to start with an initial guess, then to approximate the function by its tangent line, and finally to compute the x-intercept of this tangent line. This x-intercept will typically be a better approximation to the original function's root than the first guess, and the method can be iterated.

If the tangent line to the curve f(x) at x = xn intercepts the x-axis at xn+1 then the slope is
Solving for xn+1 gives

We start the process with some arbitrary initial value x0. (The closer to the zero, the better. But, in the absence of any intuition about where the zero might lie, a "guess and check" method might narrow the possibilities to a reasonably small interval by appealing to the intermediate value theorem.) The method will usually converge, provided this initial guess is close enough to the unknown zero, and that f′(x0) ≠ 0. Furthermore, for a zero of multiplicity 1, the convergence is at least quadratic (see Rate of convergence) in a neighbourhood of the zero, which intuitively means that the number of correct digits roughly doubles in every step. More details can be found in § Analysis below.
Householder's methods are similar but have higher order for even faster convergence. However, the extra computations required for each step can slow down the overall performance relative to Newton's method, particularly if f or its derivatives are computationally expensive to evaluate.
History
In the Old Babylonian period (19th–16th century BCE), the side of a square of known area could be effectively approximated, and this is conjectured to have been done using a special case of Newton's method, described algebraically below, by iteratively improving an initial estimate; an equivalent method can be found in Heron of Alexandria's Metrica (1st–2nd century CE), so is often called Heron's method. Jamshīd al-Kāshī used a method to solve x − N = 0 to find roots of N, a method that was algebraically equivalent to Newton's method, and in which a similar method was found in Trigonometria Britannica, published by Henry Briggs in 1633.
The method first appeared roughly in Isaac Newton's work in De analysi per aequationes numero terminorum infinitas (written in 1669, published in 1711 by William Jones) and in De metodis fluxionum et serierum infinitarum (written in 1671, translated and published as Method of Fluxions in 1736 by John Colson). However, while Newton gave the basic ideas, his method differs from the modern method given above. He applied the method only to polynomials, starting with an initial root estimate and extracting a sequence of error corrections. He used each correction to rewrite the polynomial in terms of the remaining error, and then solved for a new correction by neglecting higher-degree terms. He did not explicitly connect the method with derivatives or present a general formula. Newton applied this method to both numerical and algebraic problems, producing Taylor series in the latter case.
Newton may have derived his method from a similar, less precise method by mathematician François Viète, however, the two methods are not the same. The essence of Viète's own method can be found in the work of the Persian mathematician Sharaf al-Din al-Tusi.
The Japanese mathematician Seki Kōwa used a form of Newton's method in the 1680s to solve single-variable equations, though the connection with calculus was missing.
Newton's method was first published in 1685 in A Treatise of Algebra both Historical and Practical by John Wallis. In 1690, Joseph Raphson published a simplified description in Analysis aequationum universalis. Raphson also applied the method only to polynomials, but he avoided Newton's tedious rewriting process by extracting each successive correction from the original polynomial. This allowed him to derive a reusable iterative expression for each problem. Finally, in 1740, Thomas Simpson described Newton's method as an iterative method for solving general nonlinear equations using calculus, essentially giving the description above. In the same publication, Simpson also gives the generalization to systems of two equations and notes that Newton's method can be used for solving optimization problems by setting the gradient to zero.
Arthur Cayley in 1879 in The Newton–Fourier imaginary problem was the first to notice the difficulties in generalizing Newton's method to complex roots of polynomials with degree greater than 2 and complex initial values. This opened the way to the study of the theory of iterations of rational functions.
Practical considerations
Newton's method is a powerful technique—in general the convergence is quadratic: as the method converges on the root, the difference between the root and the approximation is squared (the number of accurate digits roughly doubles) at each step. However, there are some difficulties with the method.
Difficulty in calculating the derivative of a function
Newton's method requires that the derivative can be calculated directly. An analytical expression for the derivative may not be easily obtainable or could be expensive to evaluate. In these situations, it may be appropriate to approximate the derivative by using the slope of a line through two nearby points on the function. Using this approximation would result in something like the secant method whose convergence is slower than that of Newton's method.
Failure of the method to converge to the root
It is important to review the proof of quadratic convergence of Newton's method before implementing it. Specifically, one should review the assumptions made in the proof. For situations where the method fails to converge, it is because the assumptions made in this proof are not met.
For example, in some cases, if the first derivative is not well behaved in the neighborhood of a particular root, then it is possible that Newton's method will fail to converge no matter where the initialization is set. In some cases, Newton's method can be stabilized by using successive over-relaxation, or the speed of convergence can be increased by using the same method.
In a robust implementation of Newton's method, it is common to place limits on the number of iterations, bound the solution to an interval known to contain the root, and combine the method with a more robust root finding method.
Slow convergence for roots of multiplicity greater than 1
If the root being sought has multiplicity greater than one, the convergence rate is merely linear (errors reduced by a constant factor at each step) unless special steps are taken. When there are two or more roots that are close together then it may take many iterations before the iterates get close enough to one of them for the quadratic convergence to be apparent. However, if the multiplicity m of the root is known, the following modified algorithm preserves the quadratic convergence rate:
This is equivalent to using successive over-relaxation. On the other hand, if the multiplicity m of the root is not known, it is possible to estimate m after carrying out one or two iterations, and then use that value to increase the rate of convergence.
If the multiplicity m of the root is finite then g(x) = f(x)/f′(x) will have a root at the same location with multiplicity 1. Applying Newton's method to find the root of g(x) recovers quadratic convergence in many cases although it generally involves the second derivative of f(x). In a particularly simple case, if f(x) = x then g(x) = x/m and Newton's method finds the root in a single iteration with
Analysis
Suppose that the function f has a zero at α, i.e., f(α) = 0, and f is differentiable in a neighborhood of α.
If f is continuously differentiable and its derivative is nonzero at α, then there exists a neighborhood of α such that for all starting values x0 in that neighborhood, the sequence (xn) will converge to α.
If f is continuously differentiable, its derivative is nonzero at α, and it has a second derivative at α, then the convergence is quadratic or faster. If the second derivative is not 0 at α then the convergence is merely quadratic. If the third derivative exists and is bounded in a neighborhood of α, then:
where
If the derivative is 0 at α, then the convergence is usually only linear. Specifically, if f is twice continuously differentiable, f′(α) = 0 and f″(α) ≠ 0, then there exists a neighborhood of α such that, for all starting values x0 in that neighborhood, the sequence of iterates converges linearly, with rate 1/2. Alternatively, if f′(α) = 0 and f′(x) ≠ 0 for x ≠ α, x in a neighborhood U of α, α being a zero of multiplicity r, and if f ∈ C(U), then there exists a neighborhood of α such that, for all starting values x0 in that neighborhood, the sequence of iterates converges linearly.
However, even linear convergence is not guaranteed in pathological situations.
In practice, these results are local, and the neighborhood of convergence is not known in advance. But there are also some results on global convergence: for instance, given a right neighborhood U+ of α, if f is twice differentiable in U+ and if f′ ≠ 0, f · f″ > 0 in U+, then, for each x0 in U+ the sequence xk is monotonically decreasing to α.
Proof of quadratic convergence for Newton's iterative method
According to Taylor's theorem, any function f(x) which has a continuous second derivative can be represented by an expansion about a point that is close to a root of f(x). Suppose this root is α. Then the expansion of f(α) about xn is:
| 1 |
where the Lagrange form of the Taylor series expansion remainder is
where ξn is in between xn and α.
Since α is the root, (1) becomes:
| 2 |
Dividing equation (2) by f′(xn) and rearranging gives
| 3 |
Remembering that xn + 1 is defined by
| 4 |
one finds that
That is,
| 5 |
Taking the absolute value of both sides gives
| 6 |
Equation (6) shows that the order of convergence is at least quadratic if the following conditions are satisfied:
- f′(x) ≠ 0; for all x ∈ I, where I is the interval ;
- f″(x) is continuous, for all x ∈ I;
- M |ε0| < 1
where M is given by
If these conditions hold,
Fourier conditions
Suppose that f(x) is a concave function on an interval, which is strictly increasing. If it is negative at the left endpoint and positive at the right endpoint, the intermediate value theorem guarantees that there is a zero ζ of f somewhere in the interval. From geometrical principles, it can be seen that the Newton iteration xi starting at the left endpoint is monotonically increasing and convergent, necessarily to ζ.
Joseph Fourier introduced a modification of Newton's method starting at the right endpoint:
This sequence is monotonically decreasing and convergent. By passing to the limit in this definition, it can be seen that the limit of yi must also be the zero ζ.
So, in the case of a concave increasing function with a zero, initialization is largely irrelevant. Newton iteration starting anywhere left of the zero will converge, as will Fourier's modified Newton iteration starting anywhere right of the zero. The accuracy at any step of the iteration can be determined directly from the difference between the location of the iteration from the left and the location of the iteration from the right. If f is twice continuously differentiable, it can be proved using Taylor's theorem that
showing that this difference in locations converges quadratically to zero.
All of the above can be extended to systems of equations in multiple variables, although in that context the relevant concepts of monotonicity and concavity are more subtle to formulate. In the case of single equations in a single variable, the above monotonic convergence of Newton's method can also be generalized to replace concavity by positivity or negativity conditions on an arbitrary higher-order derivative of f. However, in this generalization, Newton's iteration is modified so as to be based on Taylor polynomials rather than the tangent line. In the case of concavity, this modification coincides with the standard Newton method.
Examples
Use of Newton's method to compute square roots
Newton's method is one of many known methods of computing square roots. Given a positive number a, the problem of finding a number x such that x = a is equivalent to finding a root of the function f(x) = x − a. The Newton iteration defined by this function is given by
This happens to coincide with the "Babylonian" method of finding square roots, which consists of replacing an approximate root xn by the arithmetic mean of xn and a⁄xn. By performing this iteration, it is possible to evaluate a square root to any desired accuracy by only using the basic arithmetic operations.
The following three tables show examples of the result of this computation for finding the square root of 612, with the iteration initialized at the values of 1, 10, and −20. Each row in a "xn" column is obtained by applying the preceding formula to the entry above it, for instance
| xn | f(xn) | xn | f(xn) | xn | f(xn) | ||
|---|---|---|---|---|---|---|---|
| 1 | −611 | 10 | −512 | −20 | −212 | ||
| 306.5 | 9.3330 × 10 | 35.6 | 655.36 | −25.3 | 28.09 | ||
| 154.2483686786 | 2.3180 × 10 | 26.3955056180 | 84.722 | −24.7448616601 | 0.30818 | ||
| 79.1079978644 | 5.6461 × 10 | 24.7906354925 | 2.5756 | −24.7386345374 | 3.8777 × 10 | ||
| 43.4221286822 | 1.2735 × 10 | 24.7386882941 | 2.6985 × 10 | −24.7386337537 | 6.1424 × 10 | ||
| 28.7581624288 | 215.03 | 24.7386337538 | 2.9746 × 10 | ||||
| 25.0195385369 | 13.977 | ||||||
| 24.7402106712 | 7.8024 × 10 | ||||||
| 24.7386338040 | 2.4865 × 10 | ||||||
| 24.7386337537 | 2.5256 × 10 |
The correct digits are underlined. It is seen that with only a few iterations one can obtain a solution accurate to many decimal places. The first table shows that this is true even if the Newton iteration were initialized by the very inaccurate guess of 1.
When computing any nonzero square root, the first derivative of f must be nonzero at the root, and that f is a smooth function. So, even before any computation, it is known that any convergent Newton iteration has a quadratic rate of convergence. This is reflected in the above tables by the fact that once a Newton iterate gets close to the root, the number of correct digits approximately doubles with each iteration.
Solution of cos(x) = x using Newton's method
Consider the problem of finding the positive number x with cos x = x. We can rephrase that as finding the zero of f(x) = cos(x) − x. We have f′(x) = −sin(x) − 3x. Since cos(x) ≤ 1 for all x and x > 1 for x > 1, we know that our solution lies between 0 and 1.
A starting value of 0 will lead to an undefined result which illustrates the importance of using a starting point close to the solution. For example, with an initial guess x0 = 0.5, the sequence given by Newton's method is:
The correct digits are underlined in the above example. In particular, x6 is correct to 12 decimal places. We see that the number of correct digits after the decimal point increases from 2 (for x3) to 5 and 10, illustrating the quadratic convergence.
Slow convergence
The function f(x) = x has a root at 0. Since f is continuously differentiable at its root, the theory guarantees that Newton's method as initialized sufficiently close to the root will converge. However, since the derivative f ′ is zero at the root, quadratic convergence is not ensured by the theory. In this particular example, the Newton iteration is given by
It is visible from this that Newton's method could be initialized anywhere and converge to zero, but at only a linear rate. If initialized at 1, dozens of iterations would be required before ten digits of accuracy are achieved.
The function f(x) = x + x also has a root at 0, where it is continuously differentiable. Although the first derivative f ′ is nonzero at the root, the second derivative f ′′ is nonexistent there, so that quadratic convergence cannot be guaranteed. In fact the Newton iteration is given by
From this, it can be seen that the rate of convergence is superlinear but subquadratic. This can be seen in the following tables, the left of which shows Newton's method applied to the above f(x) = x + x and the right of which shows Newton's method applied to f(x) = x + x. The quadratic convergence in iteration shown on the right is illustrated by the orders of magnitude in the distance from the iterate to the true root (0,1,2,3,5,10,20,39,...) being approximately doubled from row to row. While the convergence on the left is superlinear, the order of magnitude is only multiplied by about 4/3 from row to row (0,1,2,4,5,7,10,13,...).
| xn | x + x n |
xn | x + x n | |
|---|---|---|---|---|
| 1 | 2 | 1 | 2 | |
| 1.4286 × 10 | 2.1754 × 10 | 3.3333 × 10 | 4.4444 × 10 | |
| 1.4669 × 10 | 1.8260 × 10 | 6.6666 × 10 | 7.1111 × 10 | |
| 9.0241 × 10 | 9.8961 × 10 | 3.9216 × 10 | 3.9369 × 10 | |
| 2.5750 × 10 | 2.6511 × 10 | 1.5259 × 10 | 1.5259 × 10 | |
| 2.4386 × 10 | 2.4539 × 10 | 2.3283 × 10 | 2.3283 × 10 | |
| 5.0366 × 10 | 5.0406 × 10 | 5.4210 × 10 | 5.4210 × 10 | |
| 1.3344 × 10 | 1.3344 × 10 | 2.9387 × 10 | 2.9387 × 10 |
The rate of convergence is distinguished from the number of iterations required to reach a given accuracy. For example, the function f(x) = x − 1 has a root at 1. Since f ′(1) ≠ 0 and f is smooth, it is known that any Newton iteration convergent to 1 will converge quadratically. However, if initialized at 0.5, the first few iterates of Newton's method are approximately 26214, 24904, 23658, 22476, decreasing slowly, with only the 200th iterate being 1.0371. The following iterates are 1.0103, 1.00093, 1.0000082, and 1.00000000065, illustrating quadratic convergence. This highlights that quadratic convergence of a Newton iteration does not mean that only few iterates are required; this only applies once the sequence of iterates is sufficiently close to the root.
Convergence dependent on initialization
The function f(x) = x(1 + x) has a root at 0. The Newton iteration is given by
From this, it can be seen that there are three possible phenomena for a Newton iteration. If initialized strictly between ±1, the Newton iteration will converge (super-)quadratically to 0; if initialized exactly at 1 or −1, the Newton iteration will oscillate endlessly between ±1; if initialized anywhere else, the Newton iteration will diverge. This same trichotomy occurs for f(x) = arctan x.
In cases where the function in question has multiple roots, it can be difficult to control, via choice of initialization, which root (if any) is identified by Newton's method. For example, the function f(x) = x(x − 1)(x − 3)e has roots at −1, 0, 1, and 3. If initialized at −1.488, the Newton iteration converges to 0; if initialized at −1.487, it diverges to ∞; if initialized at −1.486, it converges to −1; if initialized at −1.485, it diverges to −∞; if initialized at −1.4843, it converges to 3; if initialized at −1.484, it converges to 1. This kind of subtle dependence on initialization is not uncommon; it is frequently studied in the complex plane in the form of the Newton fractal.
Divergence even when initialization is close to the root
Consider the problem of finding a root of f(x) = x. The Newton iteration is
Unless Newton's method is initialized at the exact root 0, it is seen that the sequence of iterates will fail to converge. For example, even if initialized at the reasonably accurate guess of 0.001, the first several iterates are −0.002, 0.004, −0.008, 0.016, reaching 1048.58, −2097.15, ... by the 20th iterate. This failure of convergence is not contradicted by the analytic theory, since in this case f is not differentiable at its root.
In the above example, failure of convergence is reflected by the failure of f(xn) to get closer to zero as n increases, as well as by the fact that successive iterates are growing further and further apart. However, the function f(x) = xe also has a root at 0. The Newton iteration is given by
In this example, where again f is not differentiable at the root, any Newton iteration not starting exactly at the root will diverge, but with both xn + 1 − xn and f(xn) converging to zero. This is seen in the following table showing the iterates with initialization 1:
| xn | f(xn) |
|---|---|
| 1 | 0.36788 |
| 1.6 | 9.0416 × 10 |
| 1.9342 | 2.9556 × 10 |
| 2.2048 | 1.0076 × 10 |
| 2.4396 | 3.5015 × 10 |
| 2.6505 | 1.2307 × 10 |
| 2.8437 | 4.3578 × 10 |
| 3.0232 | 1.5513 × 10 |
Although the convergence of xn + 1 − xn in this case is not very rapid, it can be proved from the iteration formula. This example highlights the possibility that a stopping criterion for Newton's method based only on the smallness of xn + 1 − xn and f(xn) might falsely identify a root.
Oscillatory behavior

It is easy to find situations for which Newton's method oscillates endlessly between two distinct values. For example, for Newton's method as applied to a function f to oscillate between 0 and 1, it is only necessary that the tangent line to f at 0 intersects the x-axis at 1 and that the tangent line to f at 1 intersects the x-axis at 0. This is the case, for example, if f(x) = x − 2x + 2. For this function, it is even the case that Newton's iteration as initialized sufficiently close to 0 or 1 will asymptotically oscillate between these values. For example, Newton's method as initialized at 0.99 yields iterates 0.99, −0.06317, 1.00628, 0.03651, 1.00196, 0.01162, 1.00020, 0.00120, 1.000002, and so on. This behavior is present despite the presence of a root of f approximately equal to −1.76929.
Undefinedness of Newton's method
In some cases, it is not even possible to perform the Newton iteration. For example, if f(x) = x − 1, then the Newton iteration is defined by
So Newton's method cannot be initialized at 0, since this would make x1 undefined. Geometrically, this is because the tangent line to f at 0 is horizontal (i.e. f ′(0) = 0), never intersecting the x-axis.
Even if the initialization is selected so that the Newton iteration can begin, the same phenomenon can block the iteration from being indefinitely continued.
If f has an incomplete domain, it is possible for Newton's method to send the iterates outside of the domain, so that it is impossible to continue the iteration. For example, the natural logarithm function f(x) = ln x has a root at 1, and is defined only for positive x. Newton's iteration in this case is given by
So if the iteration is initialized at e, the next iterate is 0; if the iteration is initialized at a value larger than e, then the next iterate is negative. In either case, the method cannot be continued.
Multidimensional formulations
Systems of equations
k variables, k functions
One may also use Newton's method to solve systems of k equations, which amounts to finding the (simultaneous) zeroes of k continuously differentiable functions This is equivalent to finding the zeroes of a single vector-valued function In the formulation given above, the scalars xn are replaced by vectors xn and instead of dividing the function f(xn) by its derivative f′(xn) one instead has to left multiply the function F(xn) by the inverse of its k × k Jacobian matrix JF(xn). This results in the expression
or, by solving the system of linear equations
for the unknown xn + 1 − xn.
k variables, m equations, with m > k
The k-dimensional variant of Newton's method can be used to solve systems of greater than k (nonlinear) equations as well if the algorithm uses the generalized inverse of the non-square Jacobian matrix J = (JJ)J instead of the inverse of J. If the nonlinear system has no solution, the method attempts to find a solution in the non-linear least squares sense. See Gauss–Newton algorithm for more information.
Example
For example, the following set of equations needs to be solved for vector of points given the vector of known values
the function vector, and Jacobian Matrix, for iteration k, and the vector of known values, are defined below.
Note that could have been rewritten to absorb and thus eliminate from the equations. The equation to solve for each iteration are
and
The iterations should be repeated until where is a value acceptably small enough to meet application requirements.
If vector is initially chosen to be that is, and and is chosen to be 1.10, then the example converges after four iterations to a value of
Iterations
The following iterations were made during the course of the solution.
Converging iteration sequence Step Variable Value 0 x = f(x) = 1 J = c = x = f(x) = 2 J = c = x = f(x) = 3 J = c = x = f(x) = 4 J = c = x = f(x) =
Complex functions
Main article: Newton fractal
When dealing with complex functions, Newton's method can be directly applied to find their zeroes. Each zero has a basin of attraction in the complex plane, the set of all starting values that cause the method to converge to that particular zero. These sets can be mapped as in the image shown. For many complex functions, the boundaries of the basins of attraction are fractals.
In some cases there are regions in the complex plane which are not in any of these basins of attraction, meaning the iterates do not converge. For example, if one uses a real initial condition to seek a root of x + 1, all subsequent iterates will be real numbers and so the iterations cannot converge to either root, since both roots are non-real. In this case almost all real initial conditions lead to chaotic behavior, while some initial conditions iterate either to infinity or to repeating cycles of any finite length.
Curt McMullen has shown that for any possible purely iterative algorithm similar to Newton's method, the algorithm will diverge on some open regions of the complex plane when applied to some polynomial of degree 4 or higher. However, McMullen gave a generally convergent algorithm for polynomials of degree 3. Also, for any polynomial, Hubbard, Schleicher, and Sutherland gave a method for selecting a set of initial points such that Newton's method will certainly converge at one of them at least.
In a Banach space
Another generalization is Newton's method to find a root of a functional F defined in a Banach space. In this case the formulation is
where F′(Xn) is the Fréchet derivative computed at Xn. One needs the Fréchet derivative to be boundedly invertible at each Xn in order for the method to be applicable. A condition for existence of and convergence to a root is given by the Newton–Kantorovich theorem.
Nash–Moser iteration
Further information: Nash–Moser theoremIn the 1950s, John Nash developed a version of the Newton's method to apply to the problem of constructing isometric embeddings of general Riemannian manifolds in Euclidean space. The loss of derivatives problem, present in this context, made the standard Newton iteration inapplicable, since it could not be continued indefinitely (much less converge). Nash's solution involved the introduction of smoothing operators into the iteration. He was able to prove the convergence of his smoothed Newton method, for the purpose of proving an implicit function theorem for isometric embeddings. In the 1960s, Jürgen Moser showed that Nash's methods were flexible enough to apply to problems beyond isometric embedding, particularly in celestial mechanics. Since then, a number of mathematicians, including Mikhael Gromov and Richard Hamilton, have found generalized abstract versions of the Nash–Moser theory. In Hamilton's formulation, the Nash–Moser theorem forms a generalization of the Banach space Newton method which takes place in certain Fréchet spaces.
Modifications
Quasi-Newton methods
When the Jacobian is unavailable or too expensive to compute at every iteration, a quasi-Newton method can be used.
Chebyshev's third-order method
| This section needs expansion. You can help by adding to it. (February 2019) |
Over p-adic numbers
In p-adic analysis, the standard method to show a polynomial equation in one variable has a p-adic root is Hensel's lemma, which uses the recursion from Newton's method on the p-adic numbers. Because of the more stable behavior of addition and multiplication in the p-adic numbers compared to the real numbers (specifically, the unit ball in the p-adics is a ring), convergence in Hensel's lemma can be guaranteed under much simpler hypotheses than in the classical Newton's method on the real line.
q-analog
Newton's method can be generalized with the q-analog of the usual derivative.
Modified Newton methods
Maehly's procedure
A nonlinear equation has multiple solutions in general. But if the initial value is not appropriate, Newton's method may not converge to the desired solution or may converge to the same solution found earlier. When we have already found N solutions of , then the next root can be found by applying Newton's method to the next equation:
This method is applied to obtain zeros of the Bessel function of the second kind.
Hirano's modified Newton method
Hirano's modified Newton method is a modification conserving the convergence of Newton method and avoiding unstableness. It is developed to solve complex polynomials.
Interval Newton's method
| This section may contain citations that do not verify the text. Please check for citation inaccuracies. (February 2019) (Learn how and when to remove this message) |
Combining Newton's method with interval arithmetic is very useful in some contexts. This provides a stopping criterion that is more reliable than the usual ones (which are a small value of the function or a small variation of the variable between consecutive iterations). Also, this may detect cases where Newton's method converges theoretically but diverges numerically because of an insufficient floating-point precision (this is typically the case for polynomials of large degree, where a very small change of the variable may change dramatically the value of the function; see Wilkinson's polynomial).
Consider f → C(X), where X is a real interval, and suppose that we have an interval extension F′ of f′, meaning that F′ takes as input an interval Y ⊆ X and outputs an interval F′(Y) such that:
We also assume that 0 ∉ F′(X), so in particular f has at most one root in X. We then define the interval Newton operator by:
where m ∈ Y. Note that the hypothesis on F′ implies that N(Y) is well defined and is an interval (see interval arithmetic for further details on interval operations). This naturally leads to the following sequence:
The mean value theorem ensures that if there is a root of f in Xk, then it is also in Xk + 1. Moreover, the hypothesis on F′ ensures that Xk + 1 is at most half the size of Xk when m is the midpoint of Y, so this sequence converges towards , where x* is the root of f in X.
If F′(X) strictly contains 0, the use of extended interval division produces a union of two intervals for N(X); multiple roots are therefore automatically separated and bounded.
Applications
Minimization and maximization problems
Main article: Newton's method in optimizationNewton's method can be used to find a minimum or maximum of a function f(x). The derivative is zero at a minimum or maximum, so local minima and maxima can be found by applying Newton's method to the derivative. The iteration becomes:
Multiplicative inverses of numbers and power series
An important application is Newton–Raphson division, which can be used to quickly find the reciprocal of a number a, using only multiplication and subtraction, that is to say the number x such that 1/x = a. We can rephrase that as finding the zero of f(x) = 1/x − a. We have f′(x) = −1/x.
Newton's iteration is
Therefore, Newton's iteration needs only two multiplications and one subtraction.
This method is also very efficient to compute the multiplicative inverse of a power series.
Solving transcendental equations
Many transcendental equations can be solved up to an arbitrary precision by using Newton's method. For example, finding the cumulative probability density function, such as a Normal distribution to fit a known probability generally involves integral functions with no known means to solve in closed form. However, computing the derivatives needed to solve them numerically with Newton's method is generally known, making numerical solutions possible. For an example, see the numerical solution to the inverse Normal cumulative distribution.
Numerical verification for solutions of nonlinear equations
A numerical verification for solutions of nonlinear equations has been established by using Newton's method multiple times and forming a set of solution candidates.
Code
The following is an example of a possible implementation of Newton's method in the Python (version 3.x) programming language for finding a root of a function f which has derivative f_prime.
The initial guess will be x0 = 1 and the function will be f(x) = x − 2 so that f′(x) = 2x.
Each new iteration of Newton's method will be denoted by x1. We will check during the computation whether the denominator (yprime) becomes too small (smaller than epsilon), which would be the case if f′(xn) ≈ 0, since otherwise a large amount of error could be introduced.
def f(x):
return x**2 - 2 # f(x) = x^2 - 2
def f_prime(x):
return 2*x # f'(x) = 2x
def newtons_method(x0, f, f_prime, tolerance, epsilon, max_iterations):
"""Newton's method
Args:
x0: The initial guess
f: The function whose root we are trying to find
f_prime: The derivative of the function
tolerance: Stop when iterations change by less than this
epsilon: Do not divide by a number smaller than this
max_iterations: The maximum number of iterations to compute
"""
for _ in range(max_iterations):
y = f(x0)
yprime = f_prime(x0)
if abs(yprime) < epsilon: # Give up if the denominator is too small
break
x1 = x0 - y / yprime # Do Newton's computation
if abs(x1 - x0) <= tolerance: # Stop when the result is within the desired tolerance
return x1 # x1 is a solution within tolerance and maximum number of iterations
x0 = x1 # Update x0 to start the process again
return None # Newton's method did not converge
See also
- Aitken's delta-squared process
- Bisection method
- Euler method
- Fast inverse square root
- Fisher scoring
- Gradient descent
- Integer square root
- Kantorovich theorem
- Laguerre's method
- Methods of computing square roots
- Newton's method in optimization
- Richardson extrapolation
- Root-finding algorithm
- Secant method
- Steffensen's method
- Subgradient method
Notes
- Fowler, David; Robson, Eleanor (1998). "Square root approximations in Old Babylonian mathematics: YBC 7289 in context". Historia Mathematica. 25 (4): 366–378. doi:10.1006/hmat.1998.2209.
- Ypma, Tjalling J. (1995). "Historical Development of the Newton-Raphson Method". SIAM Review. 37 (4): 531–551. doi:10.1137/1037125. ISSN 0036-1445. JSTOR 2132904.
- ^ Cajori, Florian (1911). "Historical Note on the Newton-Raphson Method of Approximation". The American Mathematical Monthly. 18 (2): 29–32. doi:10.2307/2973939. ISSN 0002-9890. JSTOR 2973939.
- Guicciardini, Niccolò (2009). Isaac Newton on Mathematical Certainty and Method. Transformations. Cambridge, Mass: MIT Press. pp. 158–159. ISBN 978-0-262-01317-8. OCLC 282968643.
- Ypma, Tjalling J. (1995). "Historical Development of the Newton-Raphson Method". SIAM Review. 37 (4): 531–551. doi:10.1137/1037125. ISSN 0036-1445. JSTOR 2132904.
- "Takakazu Seki - Biography". Maths History. Retrieved 27 November 2024.
- Wallis, John (1685). A Treatise of Algebra, both Historical and Practical. Oxford: Richard Davis. doi:10.3931/e-rara-8842.
- Raphson, Joseph (1697). Analysis Æequationum Universalis (in Latin) (2nd ed.). London: Thomas Bradyll. doi:10.3931/e-rara-13516.
- "Accelerated and Modified Newton Methods". Archived from the original on 24 May 2019. Retrieved 4 March 2016.
- Ryaben'kii, Victor S.; Tsynkov, Semyon V. (2006), A Theoretical Introduction to Numerical Analysis, CRC Press, p. 243, ISBN 9781584886075.
- Süli & Mayers 2003, Exercise 1.6
- ^ Ostrowski, A. M. (1973). Solution of equations in Euclidean and Banach spaces. Pure and Applied Mathematics. Vol. 9 (Third edition of 1960 original ed.). New York–London: Academic Press. MR 0359306. Zbl 0304.65002.
- Ortega and Rheinboldt, Section 13.3
- Traub, J. F. (1964). Iterative methods for the solution of equations. Prentice-Hall Series in Automatic Computation. Englewood Cliffs, NJ: Prentice-Hall, Inc. MR 0169356. Zbl 0121.11204.
- ^ J. E. Dennis, Jr. and Robert B. Schnabel. Numerical methods for unconstrained optimization and nonlinear equations. SIAM
- Anthony Ralston and Philip Rabinowitz. A first course in numerical analysis, second edition
- Yuri Nesterov. Lectures on convex optimization, second edition. Springer Optimization and its Applications, Volume 137.
- Süli & Mayers 2003.
- ^ Kenneth L. Judd. Numerical methods in economics. MIT Press
- ^ Burden, Burton; Fairs, J. Douglas; Reunolds, Albert C (July 1981). Numerical Analysis (2nd ed.). Boston, MA, United States: Prindle, Weber & Schmidt. pp. 448–452. ISBN 0-87150-314-X. OCLC 1036752194.
- Evans, Gwynne A. (1995). Practical Numerical Analysis. Chichester: John Wiley & Sons. pp. 30–33. ISBN 0471955353. OCLC 1319419671.
- Demidovich, Boris Pavlovich; Maron, Isaak Abramovich (1981). Computational Mathematics (Third ed.). Moscow: MIR Publishers. pp. 460–478. ISBN 9780828507042.
- Kiusalaas, Jaan (March 2013). Numerical Methods in Engineering with Python 3 (3rd ed.). New York: Cambridge University Press. pp. 175–176. ISBN 978-1-107-03385-6.
- This example is similar to one in reference, pages 451 and 452, but simplified to two equations instead of three.
- Henrici, Peter (1974). Applied and Computational Complex Analysis. Vol. 1. Wiley. ISBN 9780471598923.
- Strang, Gilbert (January 1991). "A chaotic search for i". The College Mathematics Journal. 22 (1): 3–12. doi:10.2307/2686733. JSTOR 2686733.
- McMullen, Curt (1987). "Families of rational maps and iterative root-finding algorithms" (PDF). Annals of Mathematics. Second Series. 125 (3): 467–493. doi:10.2307/1971408. JSTOR 1971408.
- Hubbard, John; Schleicher, Dierk; Sutherland, Scott (October 2001). "How to find all roots of complex polynomials by Newton's method". Inventiones Mathematicae. 146 (1): 1–33. Bibcode:2001InMat.146....1H. doi:10.1007/s002220100149. ISSN 0020-9910. S2CID 12603806.
- Yamamoto, Tetsuro (2001). "Historical Developments in Convergence Analysis for Newton's and Newton-like Methods". In Brezinski, C.; Wuytack, L. (eds.). Numerical Analysis: Historical Developments in the 20th Century. North-Holland. pp. 241–263. ISBN 0-444-50617-9.
- Hamilton, Richard S. (1982). "The inverse function theorem of Nash and Moser". Bulletin of the American Mathematical Society. New Series. 7 (1): 65–222. doi:10.1090/s0273-0979-1982-15004-2. MR 0656198. Zbl 0499.58003.
- Gromov, Mikhael (1986). Partial differential relations. Ergebnisse der Mathematik und ihrer Grenzgebiete (3). Vol. 9. Berlin: Springer-Verlag. doi:10.1007/978-3-662-02267-2. ISBN 3-540-12177-3. MR 0864505.
- Rajković, Predrag M.; Stanković, Miomir S.; Marinković, Slađana D. (2002). "Mean value theorems in $q$-calculus". Matematicki Vesnik. 54 (3–4): 171–178.
- Press et al. 2007
- Stoer, Josef; Bulirsch, Roland (1980). Introduction to numerical analysis. p. 279. OCLC 1244842246.
- Zhang, Shanjie; Jin, Jianming (1996). Computation of Special Functions. Wiley. ISBN 9780471119630.
- Murota, Kazuo (1982). "Global Convergence of a Modified Newton Iteration for Algebraic Equations". SIAM Journal on Numerical Analysis. 19 (4): 793–799. Bibcode:1982SJNA...19..793M. doi:10.1137/0719055.
- Moore, R. E. (1979). Methods and applications of interval analysis (Vol. 2). Siam.
- Hansen, E. (1978). Interval forms of Newtons method. Computing, 20(2), 153–163.
- Boyd, Stephen; Vandenberghe, Lieven (2004). Convex optimization. Cambridge: Cambridge University Press. doi:10.1017/CBO9780511804441. ISBN 0-521-83378-7. MR 2061575. Zbl 1058.90049.
References
- Gil, A.; Segura, J.; Temme, N. M. (2007). Numerical methods for special functions. Society for Industrial and Applied Mathematics. ISBN 978-0-89871-634-4.
- Süli, Endre; Mayers, David (2003). An Introduction to Numerical Analysis. Cambridge University Press. ISBN 0-521-00794-1.
Further reading
- Kendall E. Atkinson, An Introduction to Numerical Analysis, (1989) John Wiley & Sons, Inc, ISBN 0-471-62489-6
- Tjalling J. Ypma, Historical development of the Newton–Raphson method, SIAM Review 37 (4), 531–551, 1995. doi:10.1137/1037125.
- Bonnans, J. Frédéric; Gilbert, J. Charles; Lemaréchal, Claude; Sagastizábal, Claudia A. (2006). Numerical optimization: Theoretical and practical aspects. Universitext (Second revised ed. of translation of 1997 French ed.). Berlin: Springer-Verlag. pp. xiv+490. doi:10.1007/978-3-540-35447-5. ISBN 3-540-35445-X. MR 2265882.
- P. Deuflhard, Newton Methods for Nonlinear Problems. Affine Invariance and Adaptive Algorithms. Springer Series in Computational Mathematics, Vol. 35. Springer, Berlin, 2004. ISBN 3-540-21099-7.
- C. T. Kelley, Solving Nonlinear Equations with Newton's Method, no 1 in Fundamentals of Algorithms, SIAM, 2003. ISBN 0-89871-546-6.
- J. M. Ortega, W. C. Rheinboldt, Iterative Solution of Nonlinear Equations in Several Variables. Classics in Applied Mathematics, SIAM, 2000. ISBN 0-89871-461-3.
- Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007). "Chapter 9. Root Finding and Nonlinear Sets of Equations Importance Sampling". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.. See especially Sections 9.4, 9.6, and 9.7.
- Avriel, Mordecai (1976). Nonlinear Programming: Analysis and Methods. Prentice Hall. pp. 216–221. ISBN 0-13-623603-0.
External links
- "Newton method", Encyclopedia of Mathematics, EMS Press, 2001
- Weisstein, Eric W. "Newton's Method". MathWorld.
- Newton's method, Citizendium.
- Mathews, J., The Accelerated and Modified Newton Methods, Course notes.
- Wu, X., Roots of Equations, Course notes.
| Optimization: Algorithms, methods, and heuristics | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|  | |||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
| Root-finding algorithms | |
|---|---|
| Bracketing (no derivative) | |
| Householder | |
| Quasi-Newton | |
| Hybrid methods | |
| Polynomial methods | |
| Other methods | |






























 This is equivalent to finding the zeroes of a single vector-valued function
This is equivalent to finding the zeroes of a single vector-valued function  In the formulation given above, the scalars xn are replaced by vectors xn and instead of dividing the function f(xn) by its derivative f′(xn) one instead has to left multiply the function F(xn) by the inverse of its k × k
In the formulation given above, the scalars xn are replaced by vectors xn and instead of dividing the function f(xn) by its derivative f′(xn) one instead has to left multiply the function F(xn) by the inverse of its k × k 

 given the vector of known values
given the vector of known values 

 and Jacobian Matrix,
and Jacobian Matrix,  for iteration k, and the vector of known values,
for iteration k, and the vector of known values,  are defined below.
are defined below.

 could have been rewritten to absorb
could have been rewritten to absorb  from the equations. The equation to solve for each iteration are
from the equations. The equation to solve for each iteration are


 where
where  is a value acceptably small enough to meet application requirements.
is a value acceptably small enough to meet application requirements.
 is initially chosen to be
is initially chosen to be  that is,
that is,  and
and  and
and  is chosen to be 1.10, then the example converges after four iterations to a value of
is chosen to be 1.10, then the example converges after four iterations to a value of 



















 , then the next root can be found by applying Newton's method to the next equation:
, then the next root can be found by applying Newton's method to the next equation:





