| This article provides insufficient context for those unfamiliar with the subject. Please help improve the article by providing more context for the reader. (November 2016) (Learn how and when to remove this message) |

The Quadruplanar inversor of Sylvester and Kempe is a generalization of Hart's inversor. Like Hart's inversor, is a mechanism that provides a perfect straight line motion without sliding guides.
The mechanism was described in 1875 by James Joseph Sylvester in the journal Nature.
Like Hart's inversor, it is based on an antiparallelogram but the rather than placing the fixed, input and output points on the sides (dividing them in fixed proportion so they are all similar), Sylvester recognized that the additional points could be displaced sideways off the sides, as long as they formed similar triangles. Hart's original form is simply the degenerate case of triangles with altitude zero.
Gallery
In these diagrams:
- The antiparallelogram is highlighted in full opacity links.
- Yellow Triangles and Green Triangles are similar.
- Green Triangles are congruent with each other.
- Yellow Triangles are congruent with each other.
- Cyan links and Pink links are congruent.
- Dashed links are additional appendages to allow for a link to travel rectilinearly.
Example 1 – Sylvester–Kempe Inversor
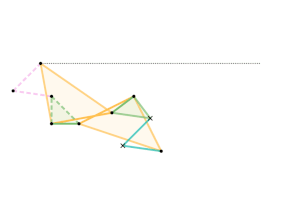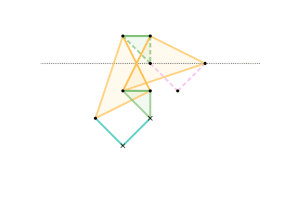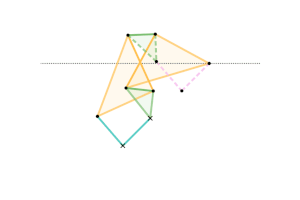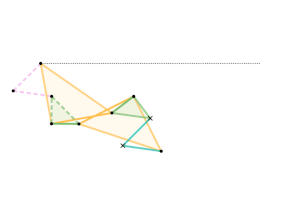
Example Dimensions:
Cyan Links =
Pink Links =
Green Triangles:
Shorter Sides =
Longest Side =
Yellow Triangles:
Shorter Sides =
Longest Side =
Example 2 – Sylvester–Kempe Inversor

Example Dimensions:
Cyan Links =
Pink Links =
Green Triangles:
Shorter Sides =
Longest Side =
Yellow Triangles:
Shorter Sides =
Longest Side =
Example 3 – Sylvester–Kempe Inversor
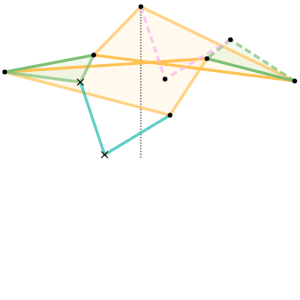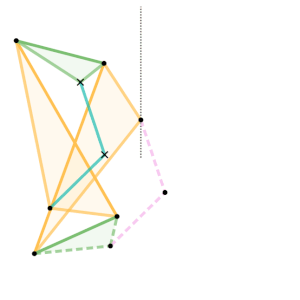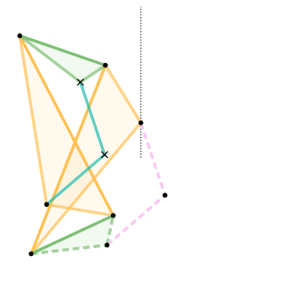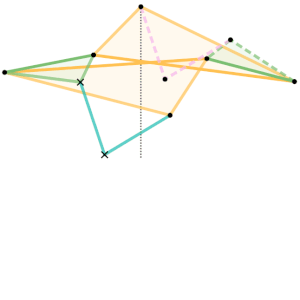
Example Dimensions:
Cyan Links =
Pink Links =
Green Triangles:
Shortest Side =
Intermediate Side =
Longest Side =
Yellow Triangles:
Shortest Side =
Intermediate Side =
Longest Side =
Example 4 – Kumara–Kampling Inversor

Created by Fumio Imai and Arglin Kampling. Rather than having the third joint of each triangular link be displaced off to the side, the third joint can also be displaced collinear to the original links, allowing for the links to remain as bars.
Example Dimensions:
Cyan Links =
Pink Links =
Green Links =
Yellow Links =
See also
- Hart's first inversor / Hart's antiparallelogram / Hart's W-frame, the origination of the Quadruplanar inversor.
- Linkage (mechanical)
- Straight line mechanism
Notes

- The midpoints must be displaced such that they not only form similar triangles, but also form a parallelogram (drawn in pink in the transition phase) if they are connected together. The triangles do not need to be right triangles, nor does the pink parallelogram have to be a rectangle. It is entirely coincidental that this happened.
References
- Sylvester, J.J. (15 July 1875). "History of the Plagiograph". Nature. XII (298): 214–216. Bibcode:1875Natur..12..214S. doi:10.1038/012214b0.
External links
- Quadruplanar Inversor Generalization – an interactive demo at GeoGebra for creating and simulating Quadruplanar Inversor linkages
- A strong relationship between new and old inversion mechanisms Dijksman, E.A., Published in: Journal of Engineering for Industry : Transactions of the ASME, Published: 01/01/1971
- https://americanhistory.si.edu/collections/search/object/nmah_1214012
- https://alexandria.tue.nl/repository/freearticles/605221.pdf














