| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In geometry, a quasiregular polyhedron is a uniform polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are vertex-transitive and edge-transitive, hence a step closer to regular polyhedra than the semiregular, which are merely vertex-transitive.
Their dual figures are face-transitive and edge-transitive; they have exactly two kinds of regular vertex figures, which alternate around each face. They are sometimes also considered quasiregular.
There are only two convex quasiregular polyhedra: the cuboctahedron and the icosidodecahedron. Their names, given by Kepler, come from recognizing that their faces are all the faces (turned differently) of the dual-pair cube and octahedron, in the first case, and of the dual-pair icosahedron and dodecahedron, in the second case.
These forms representing a pair of a regular figure and its dual can be given a vertical Schläfli symbol or r{p,q}, to represent that their faces are all the faces (turned differently) of both the regular {p,q} and the dual regular {q,p}. A quasiregular polyhedron with this symbol will have a vertex configuration p.q.p.q (or (p.q)).
More generally, a quasiregular figure can have a vertex configuration (p.q), representing r (2 or more) sequences of the faces around the vertex.
Tilings of the plane can also be quasiregular, specifically the trihexagonal tiling, with vertex configuration (3.6). Other quasiregular tilings exist on the hyperbolic plane, like the triheptagonal tiling, (3.7). Or more generally: (p.q), with 1/p + 1/q < 1/2.
Regular polyhedra and tilings with an even number of faces at each vertex can also be considered quasiregular by differentiating between faces of the same order, by representing them differently, like coloring them alternately (without defining any surface orientation). A regular figure with Schläfli symbol {p,q} can be considered quasiregular, with vertex configuration (p.p), if q is even.
Examples:
The regular octahedron, with Schläfli symbol {3,4} and 4 being even, can be considered quasiregular as a tetratetrahedron (2 sets of 4 triangles of the tetrahedron), with vertex configuration (3.3) = (3a.3b), alternating two colors of triangular faces.
The square tiling, with vertex configuration 4 and 4 being even, can be considered quasiregular, with vertex configuration (4.4) = (4a.4b), colored as a checkerboard.
The triangular tiling, with vertex configuration 3 and 6 being even, can be considered quasiregular, with vertex configuration (3.3) = (3a.3b), alternating two colors of triangular faces.
Wythoff construction
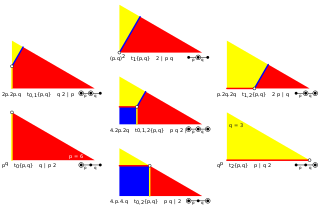 Regular (p | 2 q) and quasiregular polyhedra (2 | p q) are created from a Wythoff construction with the generator point at one of 3 corners of the fundamental domain. This defines a single edge within the fundamental domain. |
q | 2 p, p | 2 q, 2 | p q
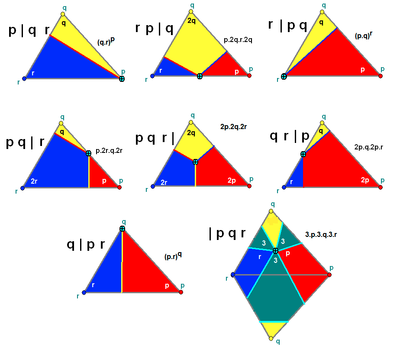
Coxeter defines a quasiregular polyhedron as one having a Wythoff symbol in the form p | q r, and it is regular if q=2 or q=r.
The Coxeter-Dynkin diagram is another symbolic representation that shows the quasiregular relation between the two dual-regular forms:
| Schläfli symbol | Coxeter diagram | Wythoff symbol | |
|---|---|---|---|
| {p,q} | q | 2 p | ||
| {q,p} | p | 2 q | ||
| r{p,q} | 2 | p q | ||
The convex quasiregular polyhedra
Further information: Rectification (geometry)There are two uniform convex quasiregular polyhedra:
- The cuboctahedron , vertex configuration (3.4), Coxeter-Dynkin diagram





- The icosidodecahedron , vertex configuration (3.5), Coxeter-Dynkin diagram





In addition, the octahedron, which is also regular, , vertex configuration (3.3), can be considered quasiregular if alternate faces are given different colors. In this form it is sometimes known as the tetratetrahedron. The remaining convex regular polyhedra have an odd number of faces at each vertex so cannot be colored in a way that preserves edge transitivity. It has Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]()
Each of these forms the common core of a dual pair of regular polyhedra. The names of two of these give clues to the associated dual pair: respectively cube octahedron, and icosahedron dodecahedron. The octahedron is the common core of a dual pair of tetrahedra (a compound known as the stella octangula); when derived in this way, the octahedron is sometimes called the tetratetrahedron, as tetrahedron tetrahedron.
| Regular | Dual regular | Quasiregular common core | Vertex figure |
|---|---|---|---|
 Tetrahedron {3,3} 3 | 2 3 |
 Tetrahedron {3,3} 3 | 2 3 |
 Tetratetrahedron r{3,3} 2 | 3 3 |
 3.3.3.3 |
 Cube {4,3} 3 | 2 4 |
 Octahedron {3,4} 4 | 2 3 |
 Cuboctahedron r{3,4} 2 | 3 4 |
 3.4.3.4 |
 Dodecahedron {5,3} 3 | 2 5 |
 Icosahedron {3,5} 5 | 2 3 |
 Icosidodecahedron r{3,5} 2 | 3 5 |
 3.5.3.5 |
Each of these quasiregular polyhedra can be constructed by a rectification operation on either regular parent, truncating the vertices fully, until each original edge is reduced to its midpoint.
Quasiregular tilings
This sequence continues as the trihexagonal tiling, vertex figure (3.6) - a quasiregular tiling based on the triangular tiling and hexagonal tiling.
| Regular | Dual regular | Quasiregular combination | Vertex figure |
|---|---|---|---|
 Hexagonal tiling {6,3} 6 | 2 3 |
 Triangular tiling {3,6} 3 | 2 6 |
 Trihexagonal tiling r{6,3} 2 | 3 6 |
 (3.6) |
The checkerboard pattern is a quasiregular coloring of the square tiling, vertex figure (4.4):
| Regular | Dual regular | Quasiregular combination | Vertex figure |
|---|---|---|---|
 {4,4} 4 | 2 4 |
 {4,4} 4 | 2 4 |
 r{4,4} 2 | 4 4 |
 (4.4) |
The triangular tiling can also be considered quasiregular, with three sets of alternating triangles at each vertex, (3.3):
 h{6,3} 3 | 3 3 |
In the hyperbolic plane, this sequence continues further, for example the triheptagonal tiling, vertex figure (3.7) - a quasiregular tiling based on the order-7 triangular tiling and heptagonal tiling.
| Regular | Dual regular | Quasiregular combination | Vertex figure |
|---|---|---|---|
 Heptagonal tiling {7,3} 7 | 2 3 |
 Triangular tiling {3,7} 3 | 2 7 |
 Triheptagonal tiling r{3,7} 2 | 3 7 |
 (3.7) |
Nonconvex examples
Coxeter, H.S.M. et al. (1954) also classify certain star polyhedra, having the same characteristics, as being quasiregular.
Two are based on dual pairs of regular Kepler–Poinsot solids, in the same way as for the convex examples:
the great icosidodecahedron , and the dodecadodecahedron :
| Regular | Dual regular | Quasiregular common core | Vertex figure |
|---|---|---|---|
 Great stellated dodecahedron {/2,3} 3 | 2 5/2 |
 Great icosahedron {3,/2} 5/2 | 2 3 |
 Great icosidodecahedron r{3,/2} 2 | 3 5/2 |
 3./2.3./2 |
 Small stellated dodecahedron {/2,5} 5 | 2 5/2 |
 Great dodecahedron {5,/2} 5/2 | 2 5 |
 Dodecadodecahedron r{5,/2} 2 | 5 5/2 |
 5./2.5./2 |
Nine more are the hemipolyhedra, which are faceted forms of the aforementioned quasiregular polyhedra derived from rectification of regular polyhedra. These include equatorial faces passing through the centre of the polyhedra:
| Quasiregular (rectified) |  Tetratetrahedron |
 Cuboctahedron |
 Icosidodecahedron |
 Great icosidodecahedron |
 Dodecadodecahedron |
|---|---|---|---|---|---|
| Quasiregular (hemipolyhedra) |  Tetrahemihexahedron /2 3 | 2 |
 Octahemioctahedron /2 3 | 3 |
 Small icosihemidodecahedron /2 3 | 5 |
 Great icosihemidodecahedron /2 3 | /3 |
 Small dodecahemicosahedron /3 /2 | 3 |
| Vertex figure |  3.4./2.4 |
 3.6./2.6 |
 3.10./2.10 |
 3./3./2./3 |
 /2.6./3.6 |
| Quasiregular (hemipolyhedra) |  Cubohemioctahedron /3 4 | 3 |
 Small dodecahemidodecahedron /4 5 | 5 |
 Great dodecahemidodecahedron /3 /2 | /3 |
 Great dodecahemicosahedron /4 5 | 3 | |
| Vertex figure |  4.6./3.6 |
 5.10./4.10 |
 /2./3./3./3 |
 5.6./4.6 |
Lastly there are three ditrigonal forms, all facetings of the regular dodecahedron, whose vertex figures contain three alternations of the two face types:
| Image | Faceted form Wythoff symbol Coxeter diagram |
Vertex figure |
|---|---|---|

|
Ditrigonal dodecadodecahedron 3 | 5/3 5 |
 (5.5/3) |

|
Small ditrigonal icosidodecahedron 3 | 5/2 3 |
 (3.5/2) |

|
Great ditrigonal icosidodecahedron 3/2 | 3 5 |
 ((3.5))/2 |
In the Euclidean plane, the sequence of hemipolyhedra continues with the following four star tilings, where apeirogons appear as the aforementioned equatorial polygons:
Quasiregular duals
Some authorities argue that, since the duals of the quasiregular solids share the same symmetries, these duals should be called quasiregular too. But not everybody uses this terminology. These duals are transitive on their edges and faces (but not on their vertices); they are the edge-transitive Catalan solids. The convex ones are, in corresponding order as above:
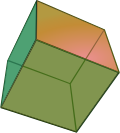
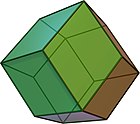
- The rhombic dodecahedron, with two types of alternating vertices, 8 with three rhombic faces, and 6 with four rhombic faces.
- The rhombic triacontahedron, with two types of alternating vertices, 20 with three rhombic faces, and 12 with five rhombic faces.
In addition, by duality with the octahedron, the cube, which is usually regular, can be made quasiregular if alternate vertices are given different colors.
Their face configurations are of the form V3.n.3.n, and Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]()
|
|

|

|

|

|
| Cube V(3.3) |
Rhombic dodecahedron V(3.4) |
Rhombic triacontahedron V(3.5) |
Rhombille tiling V(3.6) |
V(3.7) |
V(3.8) |
These three quasiregular duals are also characterised by having rhombic faces.
This rhombic-faced pattern continues as V(3.6), the rhombille tiling.
Quasiregular polytopes and honeycombs
In higher dimensions, Coxeter defined a quasiregular polytope or honeycomb to have regular facets and quasiregular vertex figures. It follows that all vertex figures are congruent and that there are two kinds of facets, which alternate.
In Euclidean 4-space, the regular 16-cell can also be seen as quasiregular as an alternated tesseract, h{4,3,3}, Coxeter diagrams: ![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() , composed of alternating tetrahedron and tetrahedron cells. Its vertex figure is the quasiregular tetratetrahedron (an octahedron with tetrahedral symmetry),
, composed of alternating tetrahedron and tetrahedron cells. Its vertex figure is the quasiregular tetratetrahedron (an octahedron with tetrahedral symmetry), ![]()
![]()
![]()
![]()
![]() .
.
The only quasiregular honeycomb in Euclidean 3-space is the alternated cubic honeycomb, h{4,3,4}, Coxeter diagrams: ![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() , composed of alternating tetrahedral and octahedral cells. Its vertex figure is the quasiregular cuboctahedron,
, composed of alternating tetrahedral and octahedral cells. Its vertex figure is the quasiregular cuboctahedron, ![]()
![]()
![]()
![]()
![]() .
.
In hyperbolic 3-space, one quasiregular honeycomb is the alternated order-5 cubic honeycomb, h{4,3,5}, Coxeter diagrams: ![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() , composed of alternating tetrahedral and icosahedral cells. Its vertex figure is the quasiregular icosidodecahedron,
, composed of alternating tetrahedral and icosahedral cells. Its vertex figure is the quasiregular icosidodecahedron, ![]()
![]()
![]()
![]()
![]() . A related paracompact alternated order-6 cubic honeycomb, h{4,3,6} has alternating tetrahedral and hexagonal tiling cells with vertex figure is a quasiregular trihexagonal tiling,
. A related paracompact alternated order-6 cubic honeycomb, h{4,3,6} has alternating tetrahedral and hexagonal tiling cells with vertex figure is a quasiregular trihexagonal tiling, ![]()
![]()
![]()
![]()
![]() .
.
| Quasiregular polychora and honeycombs: h{4,p,q} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | Finite | Affine | Compact | Paracompact | |||||||
| Schläfli symbol |
h{4,3,3} | h{4,3,4} | h{4,3,5} | h{4,3,6} | h{4,4,3} | h{4,4,4} | |||||
| Coxeter diagram |
|||||||||||
| Image | 
|

|

|

| |||||||
| Vertex figure r{p,3} |
 |
 |
 |
 |
 |
 | |||||
Regular polychora or honeycombs of the form {p,3,4} or ![]()
![]()
![]()
![]()
![]()
![]()
![]() can have their symmetry cut in half as
can have their symmetry cut in half as ![]()
![]()
![]()
![]()
![]()
![]()
![]() into quasiregular form
into quasiregular form ![]()
![]()
![]()
![]()
![]() , creating alternately colored {p,3} cells. These cases include the Euclidean cubic honeycomb {4,3,4} with cubic cells, and compact hyperbolic {5,3,4} with dodecahedral cells, and paracompact {6,3,4} with infinite hexagonal tiling cells. They have four cells around each edge, alternating in 2 colors. Their vertex figures are quasiregular tetratetrahedra,
, creating alternately colored {p,3} cells. These cases include the Euclidean cubic honeycomb {4,3,4} with cubic cells, and compact hyperbolic {5,3,4} with dodecahedral cells, and paracompact {6,3,4} with infinite hexagonal tiling cells. They have four cells around each edge, alternating in 2 colors. Their vertex figures are quasiregular tetratetrahedra, ![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]() .
.



 , same as regular octahedron
, same as regular octahedron| Regular and Quasiregular honeycombs: {p,3,4} and {p,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | Euclidean 4-space | Euclidean 3-space | Hyperbolic 3-space | ||||||||
| Name | {3,3,4} {3,3} = |
{4,3,4} {4,3} = |
{5,3,4} {5,3} = |
{6,3,4} {6,3} = | |||||||
| Coxeter diagram |
|||||||||||
| Image | 
|

|

|

| |||||||
| Cells {p,3} |
 |
 |
 |
 | |||||||
Similarly regular hyperbolic honeycombs of the form {p,3,6} or ![]()
![]()
![]()
![]()
![]()
![]()
![]() can have their symmetry cut in half as
can have their symmetry cut in half as ![]()
![]()
![]()
![]()
![]()
![]()
![]() into quasiregular form
into quasiregular form ![]()
![]()
![]()
![]()
![]() , creating alternately colored {p,3} cells. They have six cells around each edge, alternating in 2 colors. Their vertex figures are quasiregular triangular tilings,
, creating alternately colored {p,3} cells. They have six cells around each edge, alternating in 2 colors. Their vertex figures are quasiregular triangular tilings, ![]()
![]()
![]() .
.





 =
= 


| Form | Paracompact | Noncompact | |||||
|---|---|---|---|---|---|---|---|
| Name | {3,3,6} {3,3} |
{4,3,6} {4,3} |
{5,3,6} {5,3} |
{6,3,6} {6,3} |
{7,3,6} {7,3} |
{8,3,6} {8,3} |
... {∞,3,6} {∞,3} |
| Image | 
|

|

|

|

|

|

|
| Cells | {3,3} |
{4,3} |
{5,3} |
{6,3} |
{7,3} |
{8,3} |
{∞,3} |
See also
Notes
- Coxeter, H.S.M., Longuet-Higgins, M.S. and Miller, J.C.P. Uniform Polyhedra, Philosophical Transactions of the Royal Society of London 246 A (1954), pp. 401–450. (Section 7, The regular and quasiregular polyhedra p | q r)
- ^ Coxeter, Regular Polytopes, 4.7 Other honeycombs. p.69, p.88
- Coxeter, H. S. M.; Whitrow, G. J. (26 April 1950). "World-Structure and Non-Euclidean Honeycombs". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 201 (1066): 417–437. doi:10.1098/rspa.1950.0070.
References
- Cromwell, P. Polyhedra, Cambridge University Press (1977).
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 2.3 Quasi-Regular Polyhedra. (p. 17), Quasi-regular honeycombs p.69
External links
- Weisstein, Eric W. "Quasiregular polyhedron". MathWorld.
- Weisstein, Eric W. "Uniform polyhedron". MathWorld. Quasi-regular polyhedra: (p.q)
- George Hart, Quasiregular polyhedra



























 or r{p,q}, to represent that their faces are all the faces (turned differently) of both the regular {p,q} and the dual regular {q,p}. A quasiregular polyhedron with this symbol will have a
or r{p,q}, to represent that their faces are all the faces (turned differently) of both the regular {p,q} and the dual regular {q,p}. A quasiregular polyhedron with this symbol will have a 

 , vertex configuration (3.4),
, vertex configuration (3.4),  , vertex configuration (3.5), Coxeter-Dynkin diagram
, vertex configuration (3.5), Coxeter-Dynkin diagram  , vertex configuration (3.3), can be considered quasiregular if alternate faces are given different colors. In this form it is sometimes known as the tetratetrahedron. The remaining convex regular polyhedra have an odd number of faces at each vertex so cannot be colored in a way that preserves edge transitivity. It has Coxeter-Dynkin diagram
, vertex configuration (3.3), can be considered quasiregular if alternate faces are given different colors. In this form it is sometimes known as the tetratetrahedron. The remaining convex regular polyhedra have an odd number of faces at each vertex so cannot be colored in a way that preserves edge transitivity. It has Coxeter-Dynkin diagram 
 , and the
, and the  :
:

















