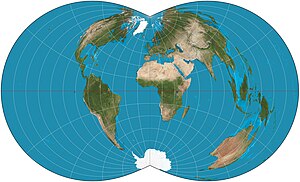
The rectangular polyconic projection is a map projection was first mentioned in 1853 by the United States Coast Survey, where it was developed and used for portions of the U.S. exceeding about one square degree. It belongs to the polyconic projection class, which consists of map projections whose parallels are non-concentric circular arcs except for the equator, which is straight. Sometimes the rectangular polyconic is called the War Office projection due to its use by the British War Office for topographic maps. It is not used much these days, with practically all military grid systems having moved onto conformal projection systems, typically modeled on the transverse Mercator projection.
Description
The rectangular polyconic has one specifiable latitude (along with the latitude of opposite sign) along which scale is correct. The scale is also true on the central meridian of the projection. Meridians are spaced such that they meet the parallels at right angles in equatorial aspect; this trait accounts for the name rectangular.
The projection is defined by:
where:
- λ is the longitude of the point to be projected;
- φ is the latitude of the point to be projected;
- λ0 is the longitude of the central meridian,
- φ0 is the latitude chosen to be the origin along λ0;
- φ1 is the latitude whose parallel is chosen to have correct scale.
To avoid division by zero, the formulas above are extended so that if φ = 0 then x = 2A and y = −φ0. If φ1= 0 then A = 1/2(λ − λ0).
See also
References
- Snyder, John P. (1993). Flattening the Earth: Two Thousand Years of Map Projections. ISBN 0-226-76747-7..
- Snyder, John P. (1989). An Album of Map Projections (PDF). Vol. U.S. Geological Survey Professional Paper 1453. United States Government Printing Office. Archived (PDF) from the original on 2012-01-19.
External links
This cartography or mapping term article is a stub. You can help Misplaced Pages by expanding it. |
