A squircle is a shape intermediate between a square and a circle. There are at least two definitions of "squircle" in use, one based on the superellipse, the other arising from work in optics. The word "squircle" is a portmanteau of the words "square" and "circle". Squircles have been applied in design and optics.
Superellipse-based squircle
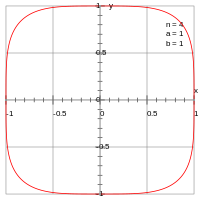
In a Cartesian coordinate system, the superellipse is defined by the equation where ra and rb are the semi-major and semi-minor axes, a and b are the x and y coordinates of the centre of the ellipse, and n is a positive number. The squircle is then defined as the superellipse with ra = rb and n = 4. Its equation is: where r is the minor radius of the squircle, and the major radius is the geometric average between square and circle. Compare this to the equation of a circle. When the squircle is centred at the origin, then a = b = 0, and it is called Lamé's special quartic.
The area inside the squircle can be expressed in terms of the gamma function Γ as where r is the minor radius of the squircle, and is the lemniscate constant.
p-norm notation
In terms of the p-norm ‖ · ‖p on R, the squircle can be expressed as: where p = 4, xc = (a, b) is the vector denoting the centre of the squircle, and x = (x, y). Effectively, this is still a "circle" of points at a distance r from the centre, but distance is defined differently. For comparison, the usual circle is the case p = 2, whereas the square is given by the p → ∞ case (the supremum norm), and a rotated square is given by p = 1 (the taxicab norm). This allows a straightforward generalization to a spherical cube, or sphube, in R, or hypersphube in higher dimensions.
Fernández-Guasti squircle
Another squircle comes from work in optics. It may be called the Fernández-Guasti squircle or FG squircle, after one of its authors, to distinguish it from the superellipse-related squircle above. This kind of squircle, centered at the origin, is defined by the equation: where r is the minor radius of the squircle, s is the squareness parameter, and x and y are in the interval [−r, r]. If s = 0, the equation is a circle; if s = 1, it is a square. This equation allows a smooth parametrization of the transition to a square from a circle, without involving infinity.
Polar form
The FG squircle's radial distance from center to edge can be described parametrically in terms of the circle radius and rotation angle:
In practice, when plotting on a computer, a small value like 0.001 can be added to the angle argument to avoid the indeterminate form when for any integer , or one can set for these cases.
Linearizing squareness
The squareness parameter in the FG squircle, while bounded between 0 and 1, results in a nonlinear interpolation of the squircle "corner" between the inner circle and the square corner. The following relationship converts to , which can then be used in the squircle formula to obtain correctly interpolated squircles:
Periodic squircle
Another type of squircle arises from trigonometry. This type of squircle is periodic in R and has the equation
where r is the minor radius of the squircle, s is the squareness parameter, and x and y are in the interval . As s approaches 0 in the limit, the equation becomes a circle. When s = 1, the equation is a square. This shape can be visualized using online graphing calculators such as Desmos.
Similar shapes

Rounded square
A shape similar to a squircle, called a rounded square, may be generated by separating four quarters of a circle and connecting their loose ends with straight lines, or by separating the four sides of a square and connecting them with quarter-circles. Such a shape is very similar but not identical to the squircle. Although constructing a rounded square may be conceptually and physically simpler, the squircle has a simpler equation and can be generalised much more easily. One consequence of this is that the squircle and other superellipses can be scaled up or down quite easily. This is useful where, for example, one wishes to create nested squircles.
Truncated circle

Another similar shape is a truncated circle, the boundary of the intersection of the regions enclosed by a square and by a concentric circle whose diameter is both greater than the length of the side of the square and less than the length of the diagonal of the square (so that each figure has interior points that are not in the interior of the other). Such shapes lack the tangent continuity possessed by both superellipses and rounded squares.
Rounded cube
A rounded cube can be defined in terms of superellipsoids.
Sphube
Similar to the name squircle, a sphube is a portmanteau of sphere and cube. It is the three-dimensional counterpart to the squircle. The equation for the FG-squircle in three dimensions is:
In polar coordinates, the sphube is expressed parametrically as
While the squareness parameter in this case does not behave identically to its squircle counterpart, nevertheless the surface is a sphere when and approaches a cube with sharp corners as .
Uses

Squircles are useful in optics. If light is passed through a two-dimensional square aperture, the central spot in the diffraction pattern can be closely modelled by a squircle or supercircle. If a rectangular aperture is used, the spot can be approximated by a superellipse.
Squircles have also been used to construct dinner plates. A squircular plate has a larger area (and can thus hold more food) than a circular one with the same radius, but still occupies the same amount of space in a rectangular or square cupboard.
Many Nokia phone models have been designed with a squircle-shaped touchpad button, as was the second generation Microsoft Zune. Apple uses an approximation of a squircle (actually a quintic superellipse) for icons in iOS, iPadOS, macOS, and the home buttons of some Apple hardware. One of the shapes for adaptive icons introduced in the Android "Oreo" operating system is a squircle. Samsung uses squircle-shaped icons in their Android software overlay One UI, and in Samsung Experience and TouchWiz.
Italian car manufacturer Fiat used numerous squircles in the interior and exterior design of the third generation Panda.
See also
References
- ^ Weisstein, Eric W. "Squircle". MathWorld.
- ^ Chamberlain Fong (2016). "Squircular Calculations". arXiv:1604.02174 .
- M. Fernández Guasti (1992). "Analytic Geometry of Some Rectilinear Figures". Int. J. Educ. Sci. Technol. 23: 895–901.
- ^ M. Fernández Guasti; A. Meléndez Cobarrubias; F.J. Renero Carrillo; A. Cornejo Rodríguez (2005). "LCD pixel shape and far-field diffraction patterns" (PDF). Optik. 116 (6): 265–269. Bibcode:2005Optik.116..265F. doi:10.1016/j.ijleo.2005.01.018. Retrieved 20 November 2006.
- ^ C. Fong (2018). Squircular Calculations. Joint Mathematics Meeting 2018, SIGMAA-ARTS. ArXiv. doi:10.48550/arXiv.1604.02174.
- C. Fong (2022). "Visualizing Squircular Implicit Surfaces". arXiv:2210.15232 .
- "Periodic Squircle in Desmos".
- "Squircle Plate". Kitchen Contraptions. Archived from the original on 1 November 2006. Retrieved 20 November 2006.
- Nokia Designer Mark Delaney mentions the squircle in a video regarding classic Nokia phone designs:
Nokia 6700 – The little black dress of phones. Archived from the original on 6 January 2010. Retrieved 9 December 2009.See 3:13 in video
- "Clayton Miller evaluates shapes on mobile phone platforms". Retrieved 2 July 2011.
- Marsal, Katie (2 September 2009). "Microsoft discontinues hard drives, "squircle" from Zune lineup". Apple Insider. Retrieved 25 August 2022.
- "The Hunt for the Squircle". Retrieved 23 May 2022.
- "Adaptive Icons". Retrieved 15 January 2018.
- "OneUI". Samsung Developers. Retrieved 2022-04-14.
- "PANDA DESIGN STORY" (PDF). Retrieved 30 December 2018.
External links
- What is the area of a Squircle? on YouTube by Matt Parker
- Online Calculator for supercircle and super-ellipse
- Web based supercircle generator
 where ra and rb are the
where ra and rb are the  where r is the minor
where r is the minor  where r is the minor radius of the squircle, and
where r is the minor radius of the squircle, and  is the
is the  where p = 4, xc = (a, b) is the vector denoting the centre of the squircle, and x = (x, y). Effectively, this is still a "circle" of points at a distance r from the centre, but distance is defined differently. For comparison, the usual circle is the case p = 2, whereas the square is given by the p → ∞ case (the
where p = 4, xc = (a, b) is the vector denoting the centre of the squircle, and x = (x, y). Effectively, this is still a "circle" of points at a distance r from the centre, but distance is defined differently. For comparison, the usual circle is the case p = 2, whereas the square is given by the p → ∞ case (the  where r is the minor radius of the squircle, s is the squareness parameter, and x and y are in the
where r is the minor radius of the squircle, s is the squareness parameter, and x and y are in the  from center to edge can be described parametrically in terms of the circle radius and rotation angle:
from center to edge can be described parametrically in terms of the circle radius and rotation angle:

 to avoid the
to avoid the  when
when  for any integer
for any integer  , or one can set
, or one can set  for these cases.
for these cases.
 in the FG squircle, while bounded between 0 and 1, results in a nonlinear interpolation of the squircle "corner" between the inner circle and the square corner. The following relationship converts
in the FG squircle, while bounded between 0 and 1, results in a nonlinear interpolation of the squircle "corner" between the inner circle and the square corner. The following relationship converts  , which can then be used in the squircle formula to obtain correctly interpolated squircles:
, which can then be used in the squircle formula to obtain correctly interpolated squircles:






 and approaches a cube with sharp corners as
and approaches a cube with sharp corners as  .
.