(Redirected from St. Venant-Kirchhoff )
Constitutive model for ideally elastic material
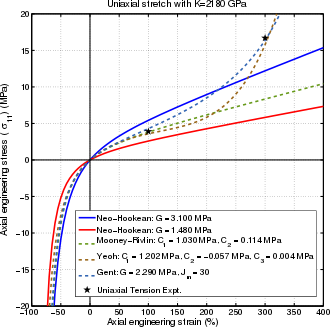
Stress–strain curves for various hyperelastic material models. A hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress–strain relationship derives from a strain energy density function . The hyperelastic material is a special case of a Cauchy elastic material .
For many materials, linear elastic models do not accurately describe the observed material behaviour. The most common example of this kind of material is rubber, whose stress -strain relationship can be defined as non-linearly elastic, isotropic and incompressible . Hyperelasticity provides a means of modeling the stress–strain behavior of such materials. The behavior of unfilled, vulcanized elastomers often conforms closely to the hyperelastic ideal. Filled elastomers and biological tissues are also often modeled via the hyperelastic idealization. In addition to being used to model physical materials, hyperelastic materials are also used as fictitious media, e.g. in the third medium contact method .
Ronald Rivlin and Melvin Mooney developed the first hyperelastic models, the Neo-Hookean and Mooney–Rivlin solids. Many other hyperelastic models have since been developed. Other widely used hyperelastic material models include the Ogden model and the Arruda–Boyce model .
Hyperelastic material models
Saint Venant–Kirchhoff model
The simplest hyperelastic material model is the Saint Venant–Kirchhoff model which is just an extension of the geometrically linear elastic material model to the geometrically nonlinear regime. This model has the general form and the isotropic form respectively
S
=
C
:
E
S
=
λ
tr
(
E
)
I
+
2
μ
E
.
{\displaystyle {\begin{aligned}{\boldsymbol {S}}&={\boldsymbol {C}}:{\boldsymbol {E}}\\{\boldsymbol {S}}&=\lambda ~{\text{tr}}({\boldsymbol {E}}){\boldsymbol {\mathit {I}}}+2\mu {\boldsymbol {E}}{\text{.}}\end{aligned}}}
:
{\displaystyle \mathbin {:} }
S
{\displaystyle {\boldsymbol {S}}}
C
:
R
3
×
3
→
R
3
×
3
{\displaystyle {\boldsymbol {C}}:\mathbb {R} ^{3\times 3}\to \mathbb {R} ^{3\times 3}}
stiffness tensor and
E
{\displaystyle {\boldsymbol {E}}}
E
=
1
2
[
(
∇
X
u
)
T
+
∇
X
u
+
(
∇
X
u
)
T
⋅
∇
X
u
]
{\displaystyle \mathbf {E} ={\frac {1}{2}}\left\,\!}
λ
{\displaystyle \lambda }
μ
{\displaystyle \mu }
Lamé constants , and
I
{\displaystyle {\boldsymbol {\mathit {I}}}}
The strain-energy density function for the Saint Venant–Kirchhoff model is
W
(
E
)
=
λ
2
[
tr
(
E
)
]
2
+
μ
tr
(
E
2
)
{\displaystyle W({\boldsymbol {E}})={\frac {\lambda }{2}}^{2}+\mu {\text{tr}}{\mathord {\left({\boldsymbol {E}}^{2}\right)}}}
and the second Piola–Kirchhoff stress can be derived from the relation
S
=
∂
W
∂
E
.
{\displaystyle {\boldsymbol {S}}={\frac {\partial W}{\partial {\boldsymbol {E}}}}~.}
Classification of hyperelastic material models
Hyperelastic material models can be classified as:
phenomenological descriptions of observed behavior
mechanistic models deriving from arguments about the underlying structure of the material
hybrids of phenomenological and mechanistic models
Generally, a hyperelastic model should satisfy the Drucker stability criterion.
Some hyperelastic models satisfy the Valanis-Landel hypothesis which states that the strain energy function can be separated into the sum of separate functions of the principal stretches
(
λ
1
,
λ
2
,
λ
3
)
{\displaystyle (\lambda _{1},\lambda _{2},\lambda _{3})}
W
=
f
(
λ
1
)
+
f
(
λ
2
)
+
f
(
λ
3
)
.
{\displaystyle W=f(\lambda _{1})+f(\lambda _{2})+f(\lambda _{3})\,.}
Stress–strain relations
Compressible hyperelastic materials
First Piola–Kirchhoff stress
If
W
(
F
)
{\displaystyle W({\boldsymbol {F}})}
1st Piola–Kirchhoff stress tensor can be calculated for a hyperelastic material as
P
=
∂
W
∂
F
or
P
i
K
=
∂
W
∂
F
i
K
.
{\displaystyle {\boldsymbol {P}}={\frac {\partial W}{\partial {\boldsymbol {F}}}}\qquad {\text{or}}\qquad P_{iK}={\frac {\partial W}{\partial F_{iK}}}.}
F
{\displaystyle {\boldsymbol {F}}}
deformation gradient . In terms of the Lagrangian Green strain (
E
{\displaystyle {\boldsymbol {E}}}
P
=
F
⋅
∂
W
∂
E
or
P
i
K
=
F
i
L
∂
W
∂
E
L
K
.
{\displaystyle {\boldsymbol {P}}={\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}\qquad {\text{or}}\qquad P_{iK}=F_{iL}~{\frac {\partial W}{\partial E_{LK}}}~.}
right Cauchy–Green deformation tensor (
C
{\displaystyle {\boldsymbol {C}}}
P
=
2
F
⋅
∂
W
∂
C
or
P
i
K
=
2
F
i
L
∂
W
∂
C
L
K
.
{\displaystyle {\boldsymbol {P}}=2~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\qquad {\text{or}}\qquad P_{iK}=2~F_{iL}~{\frac {\partial W}{\partial C_{LK}}}~.}
Second Piola–Kirchhoff stress
If
S
{\displaystyle {\boldsymbol {S}}}
second Piola–Kirchhoff stress tensor then
S
=
F
−
1
⋅
∂
W
∂
F
or
S
I
J
=
F
I
k
−
1
∂
W
∂
F
k
J
.
{\displaystyle {\boldsymbol {S}}={\boldsymbol {F}}^{-1}\cdot {\frac {\partial W}{\partial {\boldsymbol {F}}}}\qquad {\text{or}}\qquad S_{IJ}=F_{Ik}^{-1}{\frac {\partial W}{\partial F_{kJ}}}~.}
Lagrangian Green strain
S
=
∂
W
∂
E
or
S
I
J
=
∂
W
∂
E
I
J
.
{\displaystyle {\boldsymbol {S}}={\frac {\partial W}{\partial {\boldsymbol {E}}}}\qquad {\text{or}}\qquad S_{IJ}={\frac {\partial W}{\partial E_{IJ}}}~.}
right Cauchy–Green deformation tensor
S
=
2
∂
W
∂
C
or
S
I
J
=
2
∂
W
∂
C
I
J
.
{\displaystyle {\boldsymbol {S}}=2~{\frac {\partial W}{\partial {\boldsymbol {C}}}}\qquad {\text{or}}\qquad S_{IJ}=2~{\frac {\partial W}{\partial C_{IJ}}}~.}
Doyle-Ericksen formula in the material configuration.
Cauchy stress
Similarly, the Cauchy stress is given by
σ
=
1
J
∂
W
∂
F
⋅
F
T
;
J
:=
det
F
or
σ
i
j
=
1
J
∂
W
∂
F
i
K
F
j
K
.
{\displaystyle {\boldsymbol {\sigma }}={\frac {1}{J}}~{\frac {\partial W}{\partial {\boldsymbol {F}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}~;~~J:=\det {\boldsymbol {F}}\qquad {\text{or}}\qquad \sigma _{ij}={\frac {1}{J}}~{\frac {\partial W}{\partial F_{iK}}}~F_{jK}~.}
Lagrangian Green strain
σ
=
1
J
F
⋅
∂
W
∂
E
⋅
F
T
or
σ
i
j
=
1
J
F
i
K
∂
W
∂
E
K
L
F
j
L
.
{\displaystyle {\boldsymbol {\sigma }}={\frac {1}{J}}~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}\qquad {\text{or}}\qquad \sigma _{ij}={\frac {1}{J}}~F_{iK}~{\frac {\partial W}{\partial E_{KL}}}~F_{jL}~.}
right Cauchy–Green deformation tensor
σ
=
2
J
F
⋅
∂
W
∂
C
⋅
F
T
or
σ
i
j
=
2
J
F
i
K
∂
W
∂
C
K
L
F
j
L
.
{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}\qquad {\text{or}}\qquad \sigma _{ij}={\frac {2}{J}}~F_{iK}~{\frac {\partial W}{\partial C_{KL}}}~F_{jL}~.}
implicitly on reference directional quantities such as initial fiber orientations). In the special case of isotropy, the Cauchy stress can be expressed in terms of the left Cauchy-Green deformation tensor as follows:
σ
=
2
J
∂
W
∂
B
⋅
B
or
σ
i
j
=
2
J
B
i
k
∂
W
∂
B
k
j
.
{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}{\frac {\partial W}{\partial {\boldsymbol {B}}}}\cdot ~{\boldsymbol {B}}\qquad {\text{or}}\qquad \sigma _{ij}={\frac {2}{J}}~B_{ik}~{\frac {\partial W}{\partial B_{kj}}}~.}
Incompressible hyperelastic materials
For an incompressible material
J
:=
det
F
=
1
{\displaystyle J:=\det {\boldsymbol {F}}=1}
J
−
1
=
0
{\displaystyle J-1=0}
W
=
W
(
F
)
−
p
(
J
−
1
)
{\displaystyle W=W({\boldsymbol {F}})-p~(J-1)}
p
{\displaystyle p}
Lagrangian multiplier to enforce the incompressibility constraint. The 1st Piola–Kirchhoff stress now becomes
P
=
−
p
J
F
−
T
+
∂
W
∂
F
=
−
p
F
−
T
+
F
⋅
∂
W
∂
E
=
−
p
F
−
T
+
2
F
⋅
∂
W
∂
C
.
{\displaystyle {\boldsymbol {P}}=-p~J{\boldsymbol {F}}^{-{\textsf {T}}}+{\frac {\partial W}{\partial {\boldsymbol {F}}}}=-p~{\boldsymbol {F}}^{-{\textsf {T}}}+{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}=-p~{\boldsymbol {F}}^{-{\textsf {T}}}+2~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}~.}
converted into any of the other conventional stress tensors, such as the Cauchy stress tensor which is given by
σ
=
P
⋅
F
T
=
−
p
1
+
∂
W
∂
F
⋅
F
T
=
−
p
1
+
F
⋅
∂
W
∂
E
⋅
F
T
=
−
p
1
+
2
F
⋅
∂
W
∂
C
⋅
F
T
.
{\displaystyle {\boldsymbol {\sigma }}={\boldsymbol {P}}\cdot {\boldsymbol {F}}^{\textsf {T}}=-p~{\boldsymbol {\mathit {1}}}+{\frac {\partial W}{\partial {\boldsymbol {F}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}=-p~{\boldsymbol {\mathit {1}}}+{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}=-p~{\boldsymbol {\mathit {1}}}+2~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}~.}
Expressions for the Cauchy stress
Compressible isotropic hyperelastic materials
For isotropic hyperelastic materials, the Cauchy stress can be expressed in terms of the invariants of the left Cauchy–Green deformation tensor (or right Cauchy–Green deformation tensor ). If the strain energy density function is
W
(
F
)
=
W
^
(
I
1
,
I
2
,
I
3
)
=
W
¯
(
I
¯
1
,
I
¯
2
,
J
)
=
W
~
(
λ
1
,
λ
2
,
λ
3
)
,
{\displaystyle W({\boldsymbol {F}})={\hat {W}}(I_{1},I_{2},I_{3})={\bar {W}}({\bar {I}}_{1},{\bar {I}}_{2},J)={\tilde {W}}(\lambda _{1},\lambda _{2},\lambda _{3}),}
σ
=
2
I
3
[
(
∂
W
^
∂
I
1
+
I
1
∂
W
^
∂
I
2
)
B
−
∂
W
^
∂
I
2
B
⋅
B
]
+
2
I
3
∂
W
^
∂
I
3
1
=
2
J
[
1
J
2
/
3
(
∂
W
¯
∂
I
¯
1
+
I
¯
1
∂
W
¯
∂
I
¯
2
)
B
−
1
J
4
/
3
∂
W
¯
∂
I
¯
2
B
⋅
B
]
+
[
∂
W
¯
∂
J
−
2
3
J
(
I
¯
1
∂
W
¯
∂
I
¯
1
+
2
I
¯
2
∂
W
¯
∂
I
¯
2
)
]
1
=
2
J
[
(
∂
W
¯
∂
I
¯
1
+
I
¯
1
∂
W
¯
∂
I
¯
2
)
B
¯
−
∂
W
¯
∂
I
¯
2
B
¯
⋅
B
¯
]
+
[
∂
W
¯
∂
J
−
2
3
J
(
I
¯
1
∂
W
¯
∂
I
¯
1
+
2
I
¯
2
∂
W
¯
∂
I
¯
2
)
]
1
=
λ
1
λ
1
λ
2
λ
3
∂
W
~
∂
λ
1
n
1
⊗
n
1
+
λ
2
λ
1
λ
2
λ
3
∂
W
~
∂
λ
2
n
2
⊗
n
2
+
λ
3
λ
1
λ
2
λ
3
∂
W
~
∂
λ
3
n
3
⊗
n
3
{\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{\sqrt {I_{3}}}}\left+2{\sqrt {I_{3}}}~{\frac {\partial {\hat {W}}}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}\\&={\frac {2}{J}}\left+\left~{\boldsymbol {\mathit {1}}}\\&={\frac {2}{J}}\left+\left~{\boldsymbol {\mathit {1}}}\\&={\frac {\lambda _{1}}{\lambda _{1}\lambda _{2}\lambda _{3}}}~{\frac {\partial {\tilde {W}}}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\frac {\lambda _{2}}{\lambda _{1}\lambda _{2}\lambda _{3}}}~{\frac {\partial {\tilde {W}}}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+{\frac {\lambda _{3}}{\lambda _{1}\lambda _{2}\lambda _{3}}}~{\frac {\partial {\tilde {W}}}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\end{aligned}}}
the left Cauchy–Green deformation tensor for the definitions of these symbols).
Proof 1
The second Piola–Kirchhoff stress tensor for a hyperelastic material is given by
S
=
2
∂
W
∂
C
{\displaystyle {\boldsymbol {S}}=2~{\frac {\partial W}{\partial {\boldsymbol {C}}}}}
C
=
F
T
⋅
F
{\displaystyle {\boldsymbol {C}}={\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}}}
right Cauchy–Green deformation tensor and
F
{\displaystyle {\boldsymbol {F}}}
deformation gradient . The Cauchy stress is given by
σ
=
1
J
F
⋅
S
⋅
F
T
=
2
J
F
⋅
∂
W
∂
C
⋅
F
T
{\displaystyle {\boldsymbol {\sigma }}={\frac {1}{J}}~{\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}={\frac {2}{J}}~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\cdot {\boldsymbol {F}}^{T}}
J
=
det
F
{\displaystyle J=\det {\boldsymbol {F}}}
I
1
,
I
2
,
I
3
{\displaystyle I_{1},I_{2},I_{3}}
C
{\displaystyle {\boldsymbol {C}}}
∂
W
∂
C
=
∂
W
∂
I
1
∂
I
1
∂
C
+
∂
W
∂
I
2
∂
I
2
∂
C
+
∂
W
∂
I
3
∂
I
3
∂
C
.
{\displaystyle {\frac {\partial W}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\frac {\partial I_{1}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial I_{2}}}~{\frac {\partial I_{2}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial I_{3}}}~{\frac {\partial I_{3}}{\partial {\boldsymbol {C}}}}~.}
derivatives of the invariants of the symmetric tensor
C
{\displaystyle {\boldsymbol {C}}}
∂
I
1
∂
C
=
1
;
∂
I
2
∂
C
=
I
1
1
−
C
;
∂
I
3
∂
C
=
det
(
C
)
C
−
1
{\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {C}}}}={\boldsymbol {\mathit {1}}}~;~~{\frac {\partial I_{2}}{\partial {\boldsymbol {C}}}}=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {C}}~;~~{\frac {\partial I_{3}}{\partial {\boldsymbol {C}}}}=\det({\boldsymbol {C}})~{\boldsymbol {C}}^{-1}}
∂
W
∂
C
=
∂
W
∂
I
1
1
+
∂
W
∂
I
2
(
I
1
1
−
F
T
⋅
F
)
+
∂
W
∂
I
3
I
3
F
−
1
⋅
F
−
T
.
{\displaystyle {\frac {\partial W}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {\mathit {1}}}+{\frac {\partial W}{\partial I_{2}}}~(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}})+{\frac {\partial W}{\partial I_{3}}}~I_{3}~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {F}}^{-T}~.}
σ
=
2
J
[
∂
W
∂
I
1
F
⋅
F
T
+
∂
W
∂
I
2
(
I
1
F
⋅
F
T
−
F
⋅
F
T
⋅
F
⋅
F
T
)
+
∂
W
∂
I
3
I
3
1
]
{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~\left}
left Cauchy–Green deformation tensor
B
=
F
⋅
F
T
{\displaystyle {\boldsymbol {B}}={\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}}
I
3
=
J
2
{\displaystyle I_{3}=J^{2}}
σ
=
2
I
3
[
(
∂
W
∂
I
1
+
I
1
∂
W
∂
I
2
)
B
−
∂
W
∂
I
2
B
⋅
B
]
+
2
I
3
∂
W
∂
I
3
1
.
{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{\sqrt {I_{3}}}}~\left+2~{\sqrt {I_{3}}}~{\frac {\partial W}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}~.}
incompressible material
I
3
=
1
{\displaystyle I_{3}=1}
W
=
W
(
I
1
,
I
2
)
{\displaystyle W=W(I_{1},I_{2})}
∂
W
∂
C
=
∂
W
∂
I
1
∂
I
1
∂
C
+
∂
W
∂
I
2
∂
I
2
∂
C
=
∂
W
∂
I
1
1
+
∂
W
∂
I
2
(
I
1
1
−
F
T
⋅
F
)
{\displaystyle {\frac {\partial W}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\frac {\partial I_{1}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial I_{2}}}~{\frac {\partial I_{2}}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {\mathit {1}}}+{\frac {\partial W}{\partial I_{2}}}~(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}})}
σ
=
2
[
(
∂
W
∂
I
1
+
I
1
∂
W
∂
I
2
)
B
−
∂
W
∂
I
2
B
⋅
B
]
−
p
1
.
{\displaystyle {\boldsymbol {\sigma }}=2\left-p~{\boldsymbol {\mathit {1}}}~.}
p
{\displaystyle p}
Lagrange multiplier to enforce the incompressibility constraint.
If, in addition,
I
1
=
I
2
{\displaystyle I_{1}=I_{2}}
W
=
W
(
I
1
)
{\displaystyle W=W(I_{1})}
∂
W
∂
C
=
∂
W
∂
I
1
∂
I
1
∂
C
=
∂
W
∂
I
1
1
{\displaystyle {\frac {\partial W}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\frac {\partial I_{1}}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {\mathit {1}}}}
σ
=
2
∂
W
∂
I
1
B
−
p
1
.
{\displaystyle {\boldsymbol {\sigma }}=2{\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {B}}-p~{\boldsymbol {\mathit {1}}}~.}
Proof 2
The isochoric deformation gradient is defined as
F
¯
:=
J
−
1
/
3
F
{\displaystyle {\bar {\boldsymbol {F}}}:=J^{-1/3}{\boldsymbol {F}}}
B
¯
:=
F
¯
⋅
F
¯
T
=
J
−
2
/
3
B
{\displaystyle {\bar {\boldsymbol {B}}}:={\bar {\boldsymbol {F}}}\cdot {\bar {\boldsymbol {F}}}^{T}=J^{-2/3}{\boldsymbol {B}}}
B
¯
{\displaystyle {\bar {\boldsymbol {B}}}}
I
¯
1
=
tr
(
B
¯
)
=
J
−
2
/
3
tr
(
B
)
=
J
−
2
/
3
I
1
I
¯
2
=
1
2
(
tr
(
B
¯
)
2
−
tr
(
B
¯
2
)
)
=
1
2
(
(
J
−
2
/
3
tr
(
B
)
)
2
−
tr
(
J
−
4
/
3
B
2
)
)
=
J
−
4
/
3
I
2
I
¯
3
=
det
(
B
¯
)
=
J
−
6
/
3
det
(
B
)
=
J
−
2
I
3
=
J
−
2
J
2
=
1
{\displaystyle {\begin{aligned}{\bar {I}}_{1}&={\text{tr}}({\bar {\boldsymbol {B}}})=J^{-2/3}{\text{tr}}({\boldsymbol {B}})=J^{-2/3}I_{1}\\{\bar {I}}_{2}&={\frac {1}{2}}\left({\text{tr}}({\bar {\boldsymbol {B}}})^{2}-{\text{tr}}({\bar {\boldsymbol {B}}}^{2})\right)={\frac {1}{2}}\left(\left(J^{-2/3}{\text{tr}}({\boldsymbol {B}})\right)^{2}-{\text{tr}}(J^{-4/3}{\boldsymbol {B}}^{2})\right)=J^{-4/3}I_{2}\\{\bar {I}}_{3}&=\det({\bar {\boldsymbol {B}}})=J^{-6/3}\det({\boldsymbol {B}})=J^{-2}I_{3}=J^{-2}J^{2}=1\end{aligned}}}
J
{\displaystyle J}
To express the Cauchy stress in terms of the invariants
I
¯
1
,
I
¯
2
,
J
{\displaystyle {\bar {I}}_{1},{\bar {I}}_{2},J}
I
¯
1
=
J
−
2
/
3
I
1
=
I
3
−
1
/
3
I
1
;
I
¯
2
=
J
−
4
/
3
I
2
=
I
3
−
2
/
3
I
2
;
J
=
I
3
1
/
2
.
{\displaystyle {\bar {I}}_{1}=J^{-2/3}~I_{1}=I_{3}^{-1/3}~I_{1}~;~~{\bar {I}}_{2}=J^{-4/3}~I_{2}=I_{3}^{-2/3}~I_{2}~;~~J=I_{3}^{1/2}~.}
∂
W
∂
I
1
=
∂
W
∂
I
¯
1
∂
I
¯
1
∂
I
1
+
∂
W
∂
I
¯
2
∂
I
¯
2
∂
I
1
+
∂
W
∂
J
∂
J
∂
I
1
=
I
3
−
1
/
3
∂
W
∂
I
¯
1
=
J
−
2
/
3
∂
W
∂
I
¯
1
∂
W
∂
I
2
=
∂
W
∂
I
¯
1
∂
I
¯
1
∂
I
2
+
∂
W
∂
I
¯
2
∂
I
¯
2
∂
I
2
+
∂
W
∂
J
∂
J
∂
I
2
=
I
3
−
2
/
3
∂
W
∂
I
¯
2
=
J
−
4
/
3
∂
W
∂
I
¯
2
∂
W
∂
I
3
=
∂
W
∂
I
¯
1
∂
I
¯
1
∂
I
3
+
∂
W
∂
I
¯
2
∂
I
¯
2
∂
I
3
+
∂
W
∂
J
∂
J
∂
I
3
=
−
1
3
I
3
−
4
/
3
I
1
∂
W
∂
I
¯
1
−
2
3
I
3
−
5
/
3
I
2
∂
W
∂
I
¯
2
+
1
2
I
3
−
1
/
2
∂
W
∂
J
=
−
1
3
J
−
8
/
3
J
2
/
3
I
¯
1
∂
W
∂
I
¯
1
−
2
3
J
−
10
/
3
J
4
/
3
I
¯
2
∂
W
∂
I
¯
2
+
1
2
J
−
1
∂
W
∂
J
=
−
1
3
J
−
2
(
I
¯
1
∂
W
∂
I
¯
1
+
2
I
¯
2
∂
W
∂
I
¯
2
)
+
1
2
J
−
1
∂
W
∂
J
{\displaystyle {\begin{aligned}{\frac {\partial W}{\partial I_{1}}}&={\frac {\partial W}{\partial {\bar {I}}_{1}}}~{\frac {\partial {\bar {I}}_{1}}{\partial I_{1}}}+{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\frac {\partial {\bar {I}}_{2}}{\partial I_{1}}}+{\frac {\partial W}{\partial J}}~{\frac {\partial J}{\partial I_{1}}}\\&=I_{3}^{-1/3}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}=J^{-2/3}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}\\{\frac {\partial W}{\partial I_{2}}}&={\frac {\partial W}{\partial {\bar {I}}_{1}}}~{\frac {\partial {\bar {I}}_{1}}{\partial I_{2}}}+{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\frac {\partial {\bar {I}}_{2}}{\partial I_{2}}}+{\frac {\partial W}{\partial J}}~{\frac {\partial J}{\partial I_{2}}}\\&=I_{3}^{-2/3}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}=J^{-4/3}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\\{\frac {\partial W}{\partial I_{3}}}&={\frac {\partial W}{\partial {\bar {I}}_{1}}}~{\frac {\partial {\bar {I}}_{1}}{\partial I_{3}}}+{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\frac {\partial {\bar {I}}_{2}}{\partial I_{3}}}+{\frac {\partial W}{\partial J}}~{\frac {\partial J}{\partial I_{3}}}\\&=-{\frac {1}{3}}~I_{3}^{-4/3}~I_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}-{\frac {2}{3}}~I_{3}^{-5/3}~I_{2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}+{\frac {1}{2}}~I_{3}^{-1/2}~{\frac {\partial W}{\partial J}}\\&=-{\frac {1}{3}}~J^{-8/3}~J^{2/3}~{\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}-{\frac {2}{3}}~J^{-10/3}~J^{4/3}~{\bar {I}}_{2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}+{\frac {1}{2}}~J^{-1}~{\frac {\partial W}{\partial J}}\\&=-{\frac {1}{3}}~J^{-2}~\left({\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)+{\frac {1}{2}}~J^{-1}~{\frac {\partial W}{\partial J}}\end{aligned}}}
σ
=
2
I
3
[
(
∂
W
∂
I
1
+
I
1
∂
W
∂
I
2
)
B
−
∂
W
∂
I
2
B
⋅
B
]
+
2
I
3
∂
W
∂
I
3
1
.
{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{\sqrt {I_{3}}}}~\left+2~{\sqrt {I_{3}}}~{\frac {\partial W}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}~.}
I
¯
1
,
I
¯
2
,
J
{\displaystyle {\bar {I}}_{1},{\bar {I}}_{2},J}
σ
=
2
J
[
(
∂
W
∂
I
1
+
J
2
/
3
I
¯
1
∂
W
∂
I
2
)
B
−
∂
W
∂
I
2
B
⋅
B
]
+
2
J
∂
W
∂
I
3
1
.
{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~\left+2~J~{\frac {\partial W}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}~.}
W
{\displaystyle W}
I
¯
1
,
I
¯
2
,
J
{\displaystyle {\bar {I}}_{1},{\bar {I}}_{2},J}
σ
=
2
J
[
(
J
−
2
/
3
∂
W
∂
I
¯
1
+
J
−
2
/
3
I
¯
1
∂
W
∂
I
¯
2
)
B
−
J
−
4
/
3
∂
W
∂
I
¯
2
B
⋅
B
]
+
2
J
[
−
1
3
J
−
2
(
I
¯
1
∂
W
∂
I
¯
1
+
2
I
¯
2
∂
W
∂
I
¯
2
)
+
1
2
J
−
1
∂
W
∂
J
]
1
{\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{J}}~\left+\\&\qquad 2~J~\left~{\boldsymbol {\mathit {1}}}\end{aligned}}}
σ
=
2
J
[
1
J
2
/
3
(
∂
W
∂
I
¯
1
+
I
¯
1
∂
W
∂
I
¯
2
)
B
−
1
J
4
/
3
∂
W
∂
I
¯
2
B
⋅
B
]
+
[
∂
W
∂
J
−
2
3
J
(
I
¯
1
∂
W
∂
I
¯
1
+
2
I
¯
2
∂
W
∂
I
¯
2
)
]
1
{\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{J}}~\left\\&\qquad +\left{\boldsymbol {\mathit {1}}}\end{aligned}}}
B
{\displaystyle {\boldsymbol {B}}}
σ
=
2
J
[
(
∂
W
∂
I
¯
1
+
I
¯
1
∂
W
∂
I
¯
2
)
B
¯
−
∂
W
∂
I
¯
2
B
¯
⋅
B
¯
]
+
[
∂
W
∂
J
−
2
3
J
(
I
¯
1
∂
W
∂
I
¯
1
+
2
I
¯
2
∂
W
∂
I
¯
2
)
]
1
{\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{J}}~\left\\&\qquad +\left{\boldsymbol {\mathit {1}}}\end{aligned}}}
incompressible material
J
=
1
{\displaystyle J=1}
W
=
W
(
I
¯
1
,
I
¯
2
)
{\displaystyle W=W({\bar {I}}_{1},{\bar {I}}_{2})}
σ
=
2
[
(
∂
W
∂
I
¯
1
+
I
1
∂
W
∂
I
¯
2
)
B
¯
−
∂
W
∂
I
¯
2
B
¯
⋅
B
¯
]
−
p
1
.
{\displaystyle {\boldsymbol {\sigma }}=2\left-p~{\boldsymbol {\mathit {1}}}~.}
p
{\displaystyle p}
I
¯
1
=
I
¯
2
{\displaystyle {\bar {I}}_{1}={\bar {I}}_{2}}
W
=
W
(
I
¯
1
)
{\displaystyle W=W({\bar {I}}_{1})}
σ
=
2
∂
W
∂
I
¯
1
B
¯
−
p
1
.
{\displaystyle {\boldsymbol {\sigma }}=2{\frac {\partial W}{\partial {\bar {I}}_{1}}}~{\bar {\boldsymbol {B}}}-p~{\boldsymbol {\mathit {1}}}~.}
Proof 3
To express the Cauchy stress in terms of the stretches
λ
1
,
λ
2
,
λ
3
{\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}}
∂
λ
i
∂
C
=
1
2
λ
i
R
T
⋅
(
n
i
⊗
n
i
)
⋅
R
;
i
=
1
,
2
,
3
.
{\displaystyle {\frac {\partial \lambda _{i}}{\partial {\boldsymbol {C}}}}={\frac {1}{2\lambda _{i}}}~{\boldsymbol {R}}^{T}\cdot (\mathbf {n} _{i}\otimes \mathbf {n} _{i})\cdot {\boldsymbol {R}}~;~~i=1,2,3~.}
∂
W
∂
C
=
∂
W
∂
λ
1
∂
λ
1
∂
C
+
∂
W
∂
λ
2
∂
λ
2
∂
C
+
∂
W
∂
λ
3
∂
λ
3
∂
C
=
R
T
⋅
[
1
2
λ
1
∂
W
∂
λ
1
n
1
⊗
n
1
+
1
2
λ
2
∂
W
∂
λ
2
n
2
⊗
n
2
+
1
2
λ
3
∂
W
∂
λ
3
n
3
⊗
n
3
]
⋅
R
{\displaystyle {\begin{aligned}{\frac {\partial W}{\partial {\boldsymbol {C}}}}&={\frac {\partial W}{\partial \lambda _{1}}}~{\frac {\partial \lambda _{1}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial \lambda _{2}}}~{\frac {\partial \lambda _{2}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial \lambda _{3}}}~{\frac {\partial \lambda _{3}}{\partial {\boldsymbol {C}}}}\\&={\boldsymbol {R}}^{T}\cdot \left\cdot {\boldsymbol {R}}\end{aligned}}}
σ
=
2
J
F
⋅
∂
W
∂
C
⋅
F
T
=
2
J
(
V
⋅
R
)
⋅
∂
W
∂
C
⋅
(
R
T
⋅
V
)
{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\cdot {\boldsymbol {F}}^{T}={\frac {2}{J}}~({\boldsymbol {V}}\cdot {\boldsymbol {R}})\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\cdot ({\boldsymbol {R}}^{T}\cdot {\boldsymbol {V}})}
W
{\displaystyle W}
σ
=
2
J
V
⋅
[
1
2
λ
1
∂
W
∂
λ
1
n
1
⊗
n
1
+
1
2
λ
2
∂
W
∂
λ
2
n
2
⊗
n
2
+
1
2
λ
3
∂
W
∂
λ
3
n
3
⊗
n
3
]
⋅
V
{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~{\boldsymbol {V}}\cdot \left\cdot {\boldsymbol {V}}}
spectral decomposition of
V
{\displaystyle {\boldsymbol {V}}}
V
⋅
(
n
i
⊗
n
i
)
⋅
V
=
λ
i
2
n
i
⊗
n
i
;
i
=
1
,
2
,
3.
{\displaystyle {\boldsymbol {V}}\cdot (\mathbf {n} _{i}\otimes \mathbf {n} _{i})\cdot {\boldsymbol {V}}=\lambda _{i}^{2}~\mathbf {n} _{i}\otimes \mathbf {n} _{i}~;~~i=1,2,3.}
J
=
det
(
F
)
=
det
(
V
)
det
(
R
)
=
det
(
V
)
=
λ
1
λ
2
λ
3
.
{\displaystyle J=\det({\boldsymbol {F}})=\det({\boldsymbol {V}})\det({\boldsymbol {R}})=\det({\boldsymbol {V}})=\lambda _{1}\lambda _{2}\lambda _{3}~.}
σ
=
1
λ
1
λ
2
λ
3
[
λ
1
∂
W
∂
λ
1
n
1
⊗
n
1
+
λ
2
∂
W
∂
λ
2
n
2
⊗
n
2
+
λ
3
∂
W
∂
λ
3
n
3
⊗
n
3
]
{\displaystyle {\boldsymbol {\sigma }}={\frac {1}{\lambda _{1}\lambda _{2}\lambda _{3}}}~\left}
incompressible material
λ
1
λ
2
λ
3
=
1
{\displaystyle \lambda _{1}\lambda _{2}\lambda _{3}=1}
W
=
W
(
λ
1
,
λ
2
)
{\displaystyle W=W(\lambda _{1},\lambda _{2})}
σ
=
λ
1
∂
W
∂
λ
1
n
1
⊗
n
1
+
λ
2
∂
W
∂
λ
2
n
2
⊗
n
2
+
λ
3
∂
W
∂
λ
3
n
3
⊗
n
3
−
p
1
{\displaystyle {\boldsymbol {\sigma }}=\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+\lambda _{2}~{\frac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}-p~{\boldsymbol {\mathit {1}}}~}
Gateaux differentiable , but not Fréchet differentiable . A rigorous tensor derivative can only be found by solving another eigenvalue problem.
If we express the stress in terms of differences between components,
σ
11
−
σ
33
=
λ
1
∂
W
∂
λ
1
−
λ
3
∂
W
∂
λ
3
;
σ
22
−
σ
33
=
λ
2
∂
W
∂
λ
2
−
λ
3
∂
W
∂
λ
3
{\displaystyle \sigma _{11}-\sigma _{33}=\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}~;~~\sigma _{22}-\sigma _{33}=\lambda _{2}~{\frac {\partial W}{\partial \lambda _{2}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}}
λ
1
=
λ
2
{\displaystyle \lambda _{1}=\lambda _{2}}
σ
11
=
σ
22
{\displaystyle \sigma _{11}=\sigma _{22}}
σ
11
−
σ
33
=
σ
22
−
σ
33
=
λ
1
∂
W
∂
λ
1
−
λ
3
∂
W
∂
λ
3
{\displaystyle \sigma _{11}-\sigma _{33}=\sigma _{22}-\sigma _{33}=\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}}
Incompressible isotropic hyperelastic materials
For incompressible isotropic hyperelastic materials, the strain energy density function is
W
(
F
)
=
W
^
(
I
1
,
I
2
)
{\displaystyle W({\boldsymbol {F}})={\hat {W}}(I_{1},I_{2})}
σ
=
−
p
1
+
2
[
(
∂
W
^
∂
I
1
+
I
1
∂
W
^
∂
I
2
)
B
−
∂
W
^
∂
I
2
B
⋅
B
]
=
−
p
1
+
2
[
(
∂
W
∂
I
¯
1
+
I
1
∂
W
∂
I
¯
2
)
B
¯
−
∂
W
∂
I
¯
2
B
¯
⋅
B
¯
]
=
−
p
1
+
λ
1
∂
W
∂
λ
1
n
1
⊗
n
1
+
λ
2
∂
W
∂
λ
2
n
2
⊗
n
2
+
λ
3
∂
W
∂
λ
3
n
3
⊗
n
3
{\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&=-p~{\boldsymbol {\mathit {1}}}+2\left\\&=-p~{\boldsymbol {\mathit {1}}}+2\left\\&=-p~{\boldsymbol {\mathit {1}}}+\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+\lambda _{2}~{\frac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\end{aligned}}}
p
{\displaystyle p}
σ
11
−
σ
33
=
λ
1
∂
W
∂
λ
1
−
λ
3
∂
W
∂
λ
3
;
σ
22
−
σ
33
=
λ
2
∂
W
∂
λ
2
−
λ
3
∂
W
∂
λ
3
{\displaystyle \sigma _{11}-\sigma _{33}=\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}~;~~\sigma _{22}-\sigma _{33}=\lambda _{2}~{\frac {\partial W}{\partial \lambda _{2}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}}
I
1
=
I
2
{\displaystyle I_{1}=I_{2}}
σ
=
2
∂
W
∂
I
1
B
−
p
1
.
{\displaystyle {\boldsymbol {\sigma }}=2{\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {B}}-p~{\boldsymbol {\mathit {1}}}~.}
λ
1
=
λ
2
{\displaystyle \lambda _{1}=\lambda _{2}}
σ
11
−
σ
33
=
σ
22
−
σ
33
=
λ
1
∂
W
∂
λ
1
−
λ
3
∂
W
∂
λ
3
{\displaystyle \sigma _{11}-\sigma _{33}=\sigma _{22}-\sigma _{33}=\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}}
Consistency with linear elasticity
Consistency with linear elasticity is often used to determine some of the parameters of hyperelastic material models. These consistency conditions can be found by comparing Hooke's law with linearized hyperelasticity at small strains.
Consistency conditions for isotropic hyperelastic models
For isotropic hyperelastic materials to be consistent with isotropic linear elasticity , the stress–strain relation should have the following form in the infinitesimal strain limit:
σ
=
λ
t
r
(
ε
)
1
+
2
μ
ε
{\displaystyle {\boldsymbol {\sigma }}=\lambda ~\mathrm {tr} ({\boldsymbol {\varepsilon }})~{\boldsymbol {\mathit {1}}}+2\mu {\boldsymbol {\varepsilon }}}
λ
,
μ
{\displaystyle \lambda ,\mu }
Lamé constants . The strain energy density function that corresponds to the above relation is
W
=
1
2
λ
[
t
r
(
ε
)
]
2
+
μ
t
r
(
ε
2
)
{\displaystyle W={\tfrac {1}{2}}\lambda ~^{2}+\mu ~\mathrm {tr} {\mathord {\left({\boldsymbol {\varepsilon }}^{2}\right)}}}
t
r
(
ε
)
=
0
{\displaystyle \mathrm {tr} ({\boldsymbol {\varepsilon }})=0}
W
=
μ
t
r
(
ε
2
)
{\displaystyle W=\mu ~\mathrm {tr} {\mathord {\left({\boldsymbol {\varepsilon }}^{2}\right)}}}
W
(
λ
1
,
λ
2
,
λ
3
)
{\displaystyle W(\lambda _{1},\lambda _{2},\lambda _{3})}
W
(
1
,
1
,
1
)
=
0
;
∂
W
∂
λ
i
(
1
,
1
,
1
)
=
0
∂
2
W
∂
λ
i
∂
λ
j
(
1
,
1
,
1
)
=
λ
+
2
μ
δ
i
j
{\displaystyle {\begin{aligned}&W(1,1,1)=0~;~~{\frac {\partial W}{\partial \lambda _{i}}}(1,1,1)=0\\&{\frac {\partial ^{2}W}{\partial \lambda _{i}\partial \lambda _{j}}}(1,1,1)=\lambda +2\mu \delta _{ij}\end{aligned}}}
If the material is incompressible, then the above conditions may be expressed in the following form.
W
(
1
,
1
,
1
)
=
0
∂
W
∂
λ
i
(
1
,
1
,
1
)
=
∂
W
∂
λ
j
(
1
,
1
,
1
)
;
∂
2
W
∂
λ
i
2
(
1
,
1
,
1
)
=
∂
2
W
∂
λ
j
2
(
1
,
1
,
1
)
∂
2
W
∂
λ
i
∂
λ
j
(
1
,
1
,
1
)
=
i
n
d
e
p
e
n
d
e
n
t
o
f
i
,
j
≠
i
∂
2
W
∂
λ
i
2
(
1
,
1
,
1
)
−
∂
2
W
∂
λ
i
∂
λ
j
(
1
,
1
,
1
)
+
∂
W
∂
λ
i
(
1
,
1
,
1
)
=
2
μ
(
i
≠
j
)
{\displaystyle {\begin{aligned}&W(1,1,1)=0\\&{\frac {\partial W}{\partial \lambda _{i}}}(1,1,1)={\frac {\partial W}{\partial \lambda _{j}}}(1,1,1)~;~~{\frac {\partial ^{2}W}{\partial \lambda _{i}^{2}}}(1,1,1)={\frac {\partial ^{2}W}{\partial \lambda _{j}^{2}}}(1,1,1)\\&{\frac {\partial ^{2}W}{\partial \lambda _{i}\partial \lambda _{j}}}(1,1,1)=\mathrm {independentof} ~i,j\neq i\\&{\frac {\partial ^{2}W}{\partial \lambda _{i}^{2}}}(1,1,1)-{\frac {\partial ^{2}W}{\partial \lambda _{i}\partial \lambda _{j}}}(1,1,1)+{\frac {\partial W}{\partial \lambda _{i}}}(1,1,1)=2\mu ~~(i\neq j)\end{aligned}}}
Consistency conditions for incompressible I 1 based rubber materials
Many elastomers are modeled adequately by a strain energy density function that depends only on
I
1
{\displaystyle I_{1}}
W
=
W
(
I
1
)
{\displaystyle W=W(I_{1})}
I
1
=
3
,
λ
i
=
λ
j
=
1
{\displaystyle I_{1}=3,\lambda _{i}=\lambda _{j}=1}
W
(
I
1
)
|
I
1
=
3
=
0
and
∂
W
∂
I
1
|
I
1
=
3
=
μ
2
.
{\displaystyle \left.W(I_{1})\right|_{I_{1}=3}=0\quad {\text{and}}\quad \left.{\frac {\partial W}{\partial I_{1}}}\right|_{I_{1}=3}={\frac {\mu }{2}}\,.}
∂
W
∂
λ
i
=
∂
W
∂
I
1
∂
I
1
∂
λ
i
=
2
λ
i
∂
W
∂
I
1
and
∂
2
W
∂
λ
i
∂
λ
j
=
2
δ
i
j
∂
W
∂
I
1
+
4
λ
i
λ
j
∂
2
W
∂
I
1
2
.
{\displaystyle {\frac {\partial W}{\partial \lambda _{i}}}={\frac {\partial W}{\partial I_{1}}}{\frac {\partial I_{1}}{\partial \lambda _{i}}}=2\lambda _{i}{\frac {\partial W}{\partial I_{1}}}\quad {\text{and}}\quad {\frac {\partial ^{2}W}{\partial \lambda _{i}\partial \lambda _{j}}}=2\delta _{ij}{\frac {\partial W}{\partial I_{1}}}+4\lambda _{i}\lambda _{j}{\frac {\partial ^{2}W}{\partial I_{1}^{2}}}\,.}
References
^ Non-Linear Elastic Deformations , ISBN 0-486-69648-0 , Dover.
Muhr, A. H. (2005). "Modeling the stress–strain behavior of rubber". Rubber Chemistry and Technology . 78 (3): 391–425. doi :10.5254/1.3547890 .
Gao, H; Ma, X; Qi, N; Berry, C; Griffith, BE; Luo, X (2014). "A finite strain nonlinear human mitral valve model with fluid-structure interaction" . Int J Numer Methods Biomed Eng . 30 (12): 1597–613. doi :10.1002/cnm.2691 . PMC 4278556 . PMID 25319496 .
Jia, F; Ben Amar, M; Billoud, B; Charrier, B (2017). "Morphoelasticity in the development of brown alga Ectocarpus siliculosus : from cell rounding to branching" . J R Soc Interface . 14 (127): 20160596. doi :10.1098/rsif.2016.0596 . PMC 5332559 . PMID 28228537 .
Arruda, E.M.; Boyce, M.C. (1993). "A three-dimensional model for the large stretch behavior of rubber elastic materials" (PDF). J. Mech. Phys. Solids . 41 : 389–412. doi :10.1016/0022-5096(93)90013-6 . S2CID 136924401 .
Buche, M.R.; Silberstein, M.N. (2020). "Statistical mechanical constitutive theory of polymer networks: The inextricable links between distribution, behavior, and ensemble". Phys. Rev. E . 102 (1): 012501. arXiv :2004.07874 . Bibcode :2020PhRvE.102a2501B . doi :10.1103/PhysRevE.102.012501 . PMID 32794915 . S2CID 215814600 .
Rates of change of eigenvalues and eigenvectors , AIAA Journal , 6 (12) 2426–2429 (1968)
The derivatives of repeated eigenvalues and their associated eigenvectors. Journal of Vibration and Acoustics (ASME) 1996; 118:390–397.
See also
Categories :

 where
where  is tensor contraction,
is tensor contraction,  is the second Piola–Kirchhoff stress,
is the second Piola–Kirchhoff stress,  is a fourth order
is a fourth order  is the Lagrangian Green strain given by
is the Lagrangian Green strain given by

 and
and  are the
are the  is the second order unit tensor.
is the second order unit tensor.


 :
:

 is the strain energy density function, the
is the strain energy density function, the  where
where  is the
is the  In terms of the
In terms of the  )
)

 In terms of the
In terms of the  In terms of the
In terms of the  The above relation is also known as the Doyle-Ericksen formula in the material configuration.
The above relation is also known as the Doyle-Ericksen formula in the material configuration.
 In terms of the
In terms of the  In terms of the
In terms of the  The above expressions are valid even for anisotropic media (in which case, the potential function is understood to depend implicitly on reference directional quantities such as initial fiber orientations). In the special case of isotropy, the Cauchy stress can be expressed in terms of the left Cauchy-Green deformation tensor as follows:
The above expressions are valid even for anisotropic media (in which case, the potential function is understood to depend implicitly on reference directional quantities such as initial fiber orientations). In the special case of isotropy, the Cauchy stress can be expressed in terms of the left Cauchy-Green deformation tensor as follows:

 . The incompressibility constraint is therefore
. The incompressibility constraint is therefore  . To ensure incompressibility of a hyperelastic material, the strain-energy function can be written in form:
. To ensure incompressibility of a hyperelastic material, the strain-energy function can be written in form:
 where the hydrostatic pressure
where the hydrostatic pressure  functions as a
functions as a  This stress tensor can subsequently be
This stress tensor can subsequently be 
 then
then
 (See the page on
(See the page on  where
where  is the
is the  where
where  . Let
. Let  be the three principal invariants of
be the three principal invariants of  The
The  Therefore, we can write
Therefore, we can write
 Plugging into the expression for the Cauchy stress gives
Plugging into the expression for the Cauchy stress gives
 Using the
Using the  and noting that
and noting that  , we can write
, we can write
 For an
For an  and hence
and hence  .Then
.Then
 Therefore, the Cauchy stress is given by
Therefore, the Cauchy stress is given by
 where
where  , we have
, we have  and hence
and hence
 In that case the Cauchy stress can be expressed as
In that case the Cauchy stress can be expressed as

 , resulting in the isochoric deformation gradient having a determinant of 1, in other words it is volume stretch free. Using this one can subsequently define the isochoric left Cauchy–Green deformation tensor
, resulting in the isochoric deformation gradient having a determinant of 1, in other words it is volume stretch free. Using this one can subsequently define the isochoric left Cauchy–Green deformation tensor  .
The invariants of
.
The invariants of  are
are
 The set of invariants which are used to define the distortional behavior are the first two invariants of the isochoric left Cauchy–Green deformation tensor tensor, (which are identical to the ones for the right Cauchy Green stretch tensor), and add
The set of invariants which are used to define the distortional behavior are the first two invariants of the isochoric left Cauchy–Green deformation tensor tensor, (which are identical to the ones for the right Cauchy Green stretch tensor), and add  into the fray to describe the volumetric behaviour.
into the fray to describe the volumetric behaviour.
 recall that
recall that
 The chain rule of differentiation gives us
The chain rule of differentiation gives us
 Recall that the Cauchy stress is given by
Recall that the Cauchy stress is given by
 Plugging in the expressions for the derivatives of
Plugging in the expressions for the derivatives of  in terms of
in terms of  or,
or,
 In terms of the deviatoric part of
In terms of the deviatoric part of  , we can write
, we can write
 For an
For an  and hence
and hence  .Then
the Cauchy stress is given by
.Then
the Cauchy stress is given by
 where
where  , we have
, we have  and hence
the Cauchy stress can be expressed as
and hence
the Cauchy stress can be expressed as

 recall that
recall that
 The chain rule gives
The chain rule gives
 The Cauchy stress is given by
The Cauchy stress is given by
 Plugging in the expression for the derivative of
Plugging in the expression for the derivative of  Using the
Using the  we have
we have
 Also note that
Also note that
 Therefore, the expression for the Cauchy stress can be written as
Therefore, the expression for the Cauchy stress can be written as
 For an
For an  and hence
and hence  . Following Ogden p. 485, we may write
. Following Ogden p. 485, we may write
 Some care is required at this stage because, when an eigenvalue is repeated, it is in general only
Some care is required at this stage because, when an eigenvalue is repeated, it is in general only  If in addition to incompressibility we have
If in addition to incompressibility we have  then a possible solution to the problem
requires
then a possible solution to the problem
requires  and we can write the stress differences as
and we can write the stress differences as

 . The Cauchy stress is then given by
. The Cauchy stress is then given by
 where
where  where
where  are the
are the  For an incompressible material
For an incompressible material  and we have
and we have
 For any strain energy density function
For any strain energy density function  to reduce to the above forms for small strains the following conditions have to be met
to reduce to the above forms for small strains the following conditions have to be met

 These conditions can be used to find relations between the parameters of a given hyperelastic model and shear and bulk moduli.
These conditions can be used to find relations between the parameters of a given hyperelastic model and shear and bulk moduli.
 . For such materials we have
. For such materials we have  may then be expressed as
may then be expressed as
 The second consistency condition above can be derived by noting that
The second consistency condition above can be derived by noting that
 These relations can then be substituted into the consistency condition for isotropic incompressible hyperelastic materials.
These relations can then be substituted into the consistency condition for isotropic incompressible hyperelastic materials.