| Revision as of 15:42, 19 December 2004 editMsh210 (talk | contribs)Autopatrolled, Extended confirmed users, Pending changes reviewers, Rollbackers4,853 editsm Stub-sorting. You can help!← Previous edit | Latest revision as of 01:10, 25 October 2024 edit undoMonkbot (talk | contribs)Bots3,695,952 editsm Task 20: replace {lang-??} templates with {langx|??} ‹See Tfd› (Replaced 1);Tag: AWB | ||
| (358 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{short description|Astronomical equivalent of longitude}} | |||
| '''Right ascension''' (RA; symbol α: Greek letter ]) is the ] term for one of the two ]s of a point on the ] when using the ]. The other coordinate is the ]. RA is comparable to ], measured from a zero point known as the ''']'''. RA is measured in hours, minutes, and seconds. Being closely tied with ], it is both a unit of time and of angle. An '''hour of right ascension''' is equal to 15 ], a '''minute of right ascension''' equal to 15 ], and a '''second of right ascension''' equal to 15 ]. An alternative measure, used in navigation, is Sidereal Hour Angle. The main difference being that RA is measured Eastward, and SHA is measured Westward. | |||
| [[File:Ra and dec demo animation small.gif|right|thumb|350px| | |||
| RA can be used to determine a ]'s location and to determine how long it will take for a star to reach a certain point in the ]. For example, if a star with RA = 01:30:00 is at your ], then a star with RA = 20:00:00 will be in the meridian 18.5 sidereal hours later. | |||
| '''Right ascension''' and ] as seen on the inside of the ]. The primary direction of the system is the ], the ascending node of the ] (red) on the ] (blue). Right ascension is measured eastward up to 24<sup>h</sup> along the celestial equator from the primary direction.]] | |||
| '''Right ascension''' (abbreviated '''RA'''; symbol '''{{mvar|α}}''') is the ] of a particular point measured eastward along the ] from the ] at the ] to the (] of the) point in question above the Earth.<ref | |||
| >{{cite book | |||
| | author = U.S. Naval Observatory Nautical Almanac Office | |||
| | editor-last = Seidelmann | |||
| | editor-first = P. Kenneth | |||
| | title = Explanatory Supplement to the Astronomical Almanac | |||
| | publisher = University Science Books, Mill Valley, CA | |||
| | date = 1992 | |||
| |page=735 | |||
| | isbn = 0-935702-68-7}}</ref> | |||
| When paired with ], these ] specify the location of a point on the ] in the ]. | |||
| An old term, ''right ascension'' ({{langx|la|ascensio recta}})<ref | |||
| >{{cite book | |||
| |url=https://archive.org/details/guilielmiblaeui00hortgoog | |||
| |title=Institutio Astronomica | |||
| |publisher=Apud Johannem Blaeu | |||
| |date=1668 | |||
| |first=Guilielmi | |||
| |last=Blaeu | |||
| |author-link=Willem Blaeu | |||
| |page=65 | |||
| }}, "''Ascensio recta'' Solis, stellæ, aut alterius cujusdam signi, est gradus æquatorus cum quo simul exoritur in sphæra recta"; roughly translated, "''Right ascension'' of the Sun, stars, or any other sign, is the degree of the equator that rises together in a right sphere"</ref> refers to the ''ascension'', or the point on the celestial equator that rises with any ] as seen from ]'s ], where the celestial equator ] the ] at a ]. It contrasts with ''oblique ascension'', the point on the celestial equator that rises with any celestial object as seen from most ]s on Earth, where the celestial equator intersects the ] at an ].<ref | |||
| >{{cite book | |||
| |url=https://archive.org/details/bub_gb_Z1QmAAAAMAAJ | |||
| |title=A Compendious Treatise on the Use of Globes and Maps | |||
| |date=1821 | |||
| |first=John<!-- Hiram? --> | |||
| |last=Lathrop | |||
| |publisher=Wells and Lilly and J.W. Burditt, Boston | |||
| |pages=, 39 | |||
| }}</ref> | |||
| ==Explanation== | |||
| ] (green) as seen from outside the ]]] | |||
| ]s are depicted here. The symbol ♈︎ marks the ] direction. | |||
| <br />Assuming the day of the year is the March equinox: the ] lies toward the grey arrow, the star marked by a green arrow will appear to rise somewhere in the east about midnight (the Earth drawn from "above" turns anticlockwise). After the observer reaches the green arrow, dawn will over-power (see blue sky ]) the star's light for about six hours, before it sets on the western horizon. The Right ascension of the star is about 18<sup>h</sup>. 18<sup>h</sup> means it is a March early-hours star and in ] in the morning. If 12<sup>h</sup> RA, the star would be a March all-night star as ] the March equinox. If 6<sup>h</sup> RA the star would be a March late-hours star, at its high (meridian) at dusk.]] | |||
| {{main|Equatorial coordinate system}} | |||
| Right ascension is the celestial equivalent of terrestrial ]. Both right ascension and longitude measure an angle from a primary direction (a zero point) on an ]. Right ascension is measured from the Sun at the ] i.e. the ], which is the place on the ] where the Sun crosses the ] from south to north at the March ] and is currently located in the ]. Right ascension is measured continuously in a full circle from that alignment of Earth and Sun in space, that equinox, the measurement increasing towards the east.<ref | |||
| >{{cite book | |||
| |url=https://archive.org/details/anintroductiont06moulgoog | |||
| |title=An Introduction to Astronomy | |||
| |last=Moulton | |||
| |first=Forest Ray | |||
| |author-link=Forest Ray Moulton | |||
| |date=1916 | |||
| |publisher=Macmillan Co., New York | |||
| |pages=–126 | |||
| }}</ref> | |||
| As seen from Earth (except at the poles), objects noted to have 12{{Abbreviation|<sup>h</sup> RA|Hours right ascension}} are longest visible (appear throughout the night) at the March equinox; those with 0{{Abbreviation|<sup>h</sup> RA|hours right ascension}} (apart from the sun) do so at the September equinox. On those dates at midnight, such objects will reach ("culminate" at) their highest point (their meridian). How high depends on their declination; if 0° declination (i.e. on the ]) then at Earth's equator they are directly overhead (at ]). | |||
| Any ] could have been chosen for right ascension, but it is customarily measured in hours (<sup>h</sup>), minutes (<sup>m</sup>), and seconds (<sup>s</sup>), with 24<sup>h</sup> being equivalent to a ]. Astronomers have chosen this unit to measure right ascension because they measure a star's location by timing its passage through the highest point in the sky as the ]. The line which passes through the highest point in the sky, called the ], is the projection of a longitude line onto the celestial sphere. Since a complete circle contains 24<sup>h</sup> of right ascension or 360° (]), {{sfrac|1|24}} of a circle is measured as 1<sup>h</sup> of right ascension, or 15°; {{sfrac|1|1440}} of a circle is measured as 1<sup>m</sup> of right ascension, or ] (also written as 15′); and {{sfrac|1|86400}} of a circle contains 1<sup>s</sup> of right ascension, or ] (also written as 15″). A full circle, measured in right-ascension units, contains {{nobr|24 × 60 × 60 {{=}} {{val|86400}}<sup>s</sup>}}, or {{nobr|24 × 60 {{=}} {{val|1440|fmt=gaps}}<sup>m</sup>}}, or 24<sup>h</sup>.<ref>Moulton (1916), p. 126.</ref> | |||
| {{see also|Hour angle}} | |||
| Because right ascensions are measured in hours (of ]), they can be used | |||
| to time the positions of objects in the sky. For example, if a star with RA = {{nowrap|1<sup>h</sup> 30<sup>m</sup> 00<sup>s</sup>}} is at its meridian, then a star with RA = {{nowrap|20<sup>h</sup> 00<sup>m</sup> 00<sup>s</sup>}} will be on the/at its meridian (at its apparent highest point) 18.5 ] later. | |||
| Sidereal hour angle, used in ], is similar to right ascension but increases westward rather than eastward. Usually measured in degrees (°), it is the complement of right ascension with respect to 24<sup>h</sup>.<ref>''Explanatory Supplement'' (1992), p. 11.</ref> It is important not to confuse sidereal hour angle with the astronomical concept of ], which measures the angular distance of an object westward from the local ]. | |||
| ==Symbols and abbreviations== | |||
| {| class="wikitable" style="margin: 0 auto" | |||
| |- | |||
| ! scope="col" | Unit !! scope="col" | Value !! scope="col" | Symbol !! scope="col" | ] system !! scope="col" | In ] | |||
| |- | |||
| ! Hour | |||
| | {{sfrac|1|24}} circle || align="center"|<sup>h</sup> || 15]|| align="right"|{{sfrac|{{pi}}|12}} rad | |||
| |- | |||
| ! Minute | |||
| | {{sfrac|1|60}} hour, {{sfrac|1|{{val|1440|fmt=gaps}}}} circle || align="center"|<sup>m</sup> || {{sfrac|1|4}}°, 15]||align="right"|{{sfrac|{{pi}}|720}} rad | |||
| |- | |||
| ! Second | |||
| | {{sfrac|1|60}} minute, {{sfrac|1|{{val|3600|fmt=gaps}}}} hour, {{sfrac|1|{{val|86400}}}} circle || align="center"|<sup>s</sup> || {{sfrac|1|240}}°, {{sfrac|1|4}}′, 15]||align="right"| {{sfrac|{{pi}}|{{val|43200}}}} rad | |||
| |} | |||
| == Effects of precession == | |||
| {{main|Axial precession}} | |||
| The Earth's axis traces a small circle (relative to its celestial equator) slowly westward about the ]s, completing one cycle in about 26,000 years. This movement, known as ], causes the coordinates of stationary celestial objects to change continuously, if rather slowly. Therefore, ] (including right ascension) are inherently relative to the year of their observation, and astronomers specify them with reference to a particular year, known as an ]. Coordinates from different epochs must be mathematically rotated to match each other, or to match a standard epoch.<ref>Moulton (1916), pp. 92–95.</ref> Right ascension for "fixed stars" on the equator increases by about 3.1 seconds per year or 5.1 minutes per century, but for fixed stars away from the equator the rate of change can be anything from negative infinity to positive infinity. (To this must be added the ] of a star.) Over a precession cycle of 26,000 years, "fixed stars" that are far from the ]s increase in right ascension by 24h, or about 5.6' per century, whereas stars within 23.5° of an ecliptic pole undergo a net change of{{nbsp}}0h. The right ascension of ] is increasing quickly{{mdash}}in AD 2000 it was 2.5h, but when it gets closest to the north celestial pole in 2100 its right ascension will be 6h. The ] in ] and the ] in ] are always at right ascension 18<sup>h</sup> and 6<sup>h</sup> respectively. | |||
| The currently used standard epoch is ], which is January 1, 2000 at 12:00 ]. The prefix "J" indicates that it is a ]. Prior to J2000.0, astronomers used the successive ] B1875.0, B1900.0, and B1950.0.<ref>see, for instance, {{cite book | |||
| | author1 = U.S. Naval Observatory Nautical Almanac Office | |||
| | author2 = U.K. Hydrographic Office | |||
| | author3 = H.M. Nautical Almanac Office | |||
| | title = The Astronomical Almanac for the Year 2010 | |||
| | publisher = U.S. Govt. Printing Office | |||
| | date = 2008 | |||
| | page=B2 | |||
| | chapter=Time Scales and Coordinate Systems, 2010 }}</ref> | |||
| ==History== | |||
| {{Refimprove section|date=May 2012}} | |||
| ] (red) which rose or set at the same time as an object (green) on the ]. As seen from the equator, both were on a ] from pole to pole (left, ''sphaera recta'' or right sphere). From almost anywhere else, they were not (center, ''sphaera obliqua'' or oblique sphere). At the poles, objects did not rise or set (right, ''sphaera parallela'' or parallel sphere). An object's right ascension was its ascension on a right sphere.<ref>Blaeu (1668), p. 40–41.</ref>]] | |||
| The concept of right ascension has been known at least as far back as ] who measured stars in equatorial coordinates in the 2nd century BC. But Hipparchus and his successors made their ]s in ], and the use of RA was limited to special cases. | |||
| With the invention of the ], it became possible for astronomers to observe celestial objects in greater detail, provided that the telescope could be kept pointed at the object for a period of time. The easiest way to do that is to use an ], which allows the telescope to be aligned with one of its two pivots parallel to the Earth's axis. A motorized clock drive often is used with an equatorial mount to cancel out the ]. As the equatorial mount became widely adopted for observation, the equatorial coordinate system, which includes right ascension, was adopted at the same time for simplicity. Equatorial mounts could then be accurately pointed at objects with known right ascension and declination by the use of ]. The first star catalog to use right ascension and declination was ]'s '']'' (1712, 1725). | |||
| {{-}} | |||
| ] (at right, at the intersection of the ] (red) and the ] (green)) and increases eastward (towards the left). The lines of right ascension (blue) from pole to pole divide the sky into 24 hours, each equivalent to 15°.]] | |||
| ==See also== | ==See also== | ||
| {{columns-list|colwidth=30em| | |||
| *] | |||
| *] | * ] | ||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| }} | |||
| ==Notes and references== | |||
| {{astro-stub}} | |||
| {{reflist}} | |||
| == External links == | |||
| ] | |||
| * James B. Kaler, University of Illinois | |||
| ] | |||
| * University of Nebraska-Lincoln | |||
| ] | |||
| * University of Nebraska-Lincoln | |||
| ] | |||
| * {{cite web|last=Merrifield|first=Michael|title=(α,δ) – Right Ascension & Declination|url=http://www.sixtysymbols.com/videos/declination.htm|work=Sixty Symbols|publisher=] for the ]}} | |||
| ] | |||
| * (]) – to determine '''RA'''/]. | |||
| ] | |||
| ] | |||
| {{Portal bar|Astronomy|Stars|Spaceflight|Outer space|Solar System}} | |||
| ] | |||
| {{Authority control}} | |||
| ] | |||
| {{DEFAULTSORT:Right Ascension}} | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 01:10, 25 October 2024
Astronomical equivalent of longitude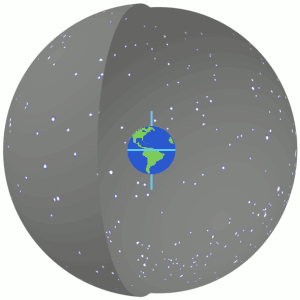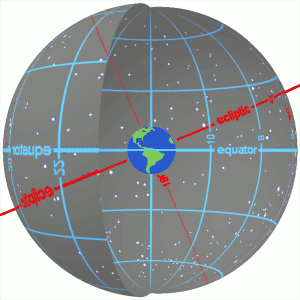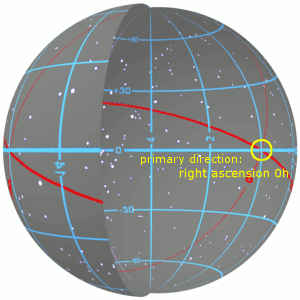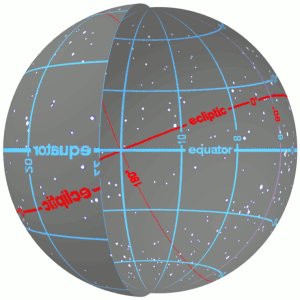
Right ascension (abbreviated RA; symbol α) is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the March equinox to the (hour circle of the) point in question above the Earth. When paired with declination, these astronomical coordinates specify the location of a point on the celestial sphere in the equatorial coordinate system.
An old term, right ascension (Latin: ascensio recta) refers to the ascension, or the point on the celestial equator that rises with any celestial object as seen from Earth's equator, where the celestial equator intersects the horizon at a right angle. It contrasts with oblique ascension, the point on the celestial equator that rises with any celestial object as seen from most latitudes on Earth, where the celestial equator intersects the horizon at an oblique angle.
Explanation


Assuming the day of the year is the March equinox: the Sun lies toward the grey arrow, the star marked by a green arrow will appear to rise somewhere in the east about midnight (the Earth drawn from "above" turns anticlockwise). After the observer reaches the green arrow, dawn will over-power (see blue sky Rayleigh scattering) the star's light for about six hours, before it sets on the western horizon. The Right ascension of the star is about 18. 18 means it is a March early-hours star and in blue sky in the morning. If 12 RA, the star would be a March all-night star as opposite the March equinox. If 6 RA the star would be a March late-hours star, at its high (meridian) at dusk.
Right ascension is the celestial equivalent of terrestrial longitude. Both right ascension and longitude measure an angle from a primary direction (a zero point) on an equator. Right ascension is measured from the Sun at the March equinox i.e. the First Point of Aries, which is the place on the celestial sphere where the Sun crosses the celestial equator from south to north at the March equinox and is currently located in the constellation Pisces. Right ascension is measured continuously in a full circle from that alignment of Earth and Sun in space, that equinox, the measurement increasing towards the east.
As seen from Earth (except at the poles), objects noted to have 12 RA are longest visible (appear throughout the night) at the March equinox; those with 0 RA (apart from the sun) do so at the September equinox. On those dates at midnight, such objects will reach ("culminate" at) their highest point (their meridian). How high depends on their declination; if 0° declination (i.e. on the celestial equator) then at Earth's equator they are directly overhead (at zenith).
Any angular unit could have been chosen for right ascension, but it is customarily measured in hours (), minutes (), and seconds (), with 24 being equivalent to a full circle. Astronomers have chosen this unit to measure right ascension because they measure a star's location by timing its passage through the highest point in the sky as the Earth rotates. The line which passes through the highest point in the sky, called the meridian, is the projection of a longitude line onto the celestial sphere. Since a complete circle contains 24 of right ascension or 360° (degrees of arc), 1/24 of a circle is measured as 1 of right ascension, or 15°; 1/1440 of a circle is measured as 1 of right ascension, or 15 minutes of arc (also written as 15′); and 1/86400 of a circle contains 1 of right ascension, or 15 seconds of arc (also written as 15″). A full circle, measured in right-ascension units, contains 24 × 60 × 60 = 86400, or 24 × 60 = 1440, or 24.
See also: Hour angleBecause right ascensions are measured in hours (of rotation of the Earth), they can be used to time the positions of objects in the sky. For example, if a star with RA = 1 30 00 is at its meridian, then a star with RA = 20 00 00 will be on the/at its meridian (at its apparent highest point) 18.5 sidereal hours later.
Sidereal hour angle, used in celestial navigation, is similar to right ascension but increases westward rather than eastward. Usually measured in degrees (°), it is the complement of right ascension with respect to 24. It is important not to confuse sidereal hour angle with the astronomical concept of hour angle, which measures the angular distance of an object westward from the local meridian.
Symbols and abbreviations
| Unit | Value | Symbol | Sexagesimal system | In radians |
|---|---|---|---|---|
| Hour | 1/24 circle | 15° | π/12 rad | |
| Minute | 1/60 hour, 1/1440 circle | 1/4°, 15′ | π/720 rad | |
| Second | 1/60 minute, 1/3600 hour, 1/86400 circle | 1/240°, 1/4′, 15″ | π/43200 rad |
Effects of precession
Main article: Axial precessionThe Earth's axis traces a small circle (relative to its celestial equator) slowly westward about the celestial poles, completing one cycle in about 26,000 years. This movement, known as precession, causes the coordinates of stationary celestial objects to change continuously, if rather slowly. Therefore, equatorial coordinates (including right ascension) are inherently relative to the year of their observation, and astronomers specify them with reference to a particular year, known as an epoch. Coordinates from different epochs must be mathematically rotated to match each other, or to match a standard epoch. Right ascension for "fixed stars" on the equator increases by about 3.1 seconds per year or 5.1 minutes per century, but for fixed stars away from the equator the rate of change can be anything from negative infinity to positive infinity. (To this must be added the proper motion of a star.) Over a precession cycle of 26,000 years, "fixed stars" that are far from the ecliptic poles increase in right ascension by 24h, or about 5.6' per century, whereas stars within 23.5° of an ecliptic pole undergo a net change of 0h. The right ascension of Polaris is increasing quickly—in AD 2000 it was 2.5h, but when it gets closest to the north celestial pole in 2100 its right ascension will be 6h. The North Ecliptic Pole in Draco and the South Ecliptic Pole in Dorado are always at right ascension 18 and 6 respectively.
The currently used standard epoch is J2000.0, which is January 1, 2000 at 12:00 TT. The prefix "J" indicates that it is a Julian epoch. Prior to J2000.0, astronomers used the successive Besselian epochs B1875.0, B1900.0, and B1950.0.
History
| This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (May 2012) (Learn how and when to remove this message) |
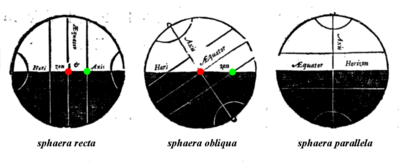
The concept of right ascension has been known at least as far back as Hipparchus who measured stars in equatorial coordinates in the 2nd century BC. But Hipparchus and his successors made their star catalogs in ecliptic coordinates, and the use of RA was limited to special cases.
With the invention of the telescope, it became possible for astronomers to observe celestial objects in greater detail, provided that the telescope could be kept pointed at the object for a period of time. The easiest way to do that is to use an equatorial mount, which allows the telescope to be aligned with one of its two pivots parallel to the Earth's axis. A motorized clock drive often is used with an equatorial mount to cancel out the Earth's rotation. As the equatorial mount became widely adopted for observation, the equatorial coordinate system, which includes right ascension, was adopted at the same time for simplicity. Equatorial mounts could then be accurately pointed at objects with known right ascension and declination by the use of setting circles. The first star catalog to use right ascension and declination was John Flamsteed's Historia Coelestis Britannica (1712, 1725).

See also
- Celestial coordinate system
- Celestial pole
- Declination
- Ecliptic
- Equatorial coordinate system
- Equinoctial colure
- Geographic coordinate system
- Hour angle
- Right ascension of the ascending node (RAAN)
- Setting circles
- Sidereal time
Notes and references
- U.S. Naval Observatory Nautical Almanac Office (1992). Seidelmann, P. Kenneth (ed.). Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. p. 735. ISBN 0-935702-68-7.
- Blaeu, Guilielmi (1668). Institutio Astronomica. Apud Johannem Blaeu. p. 65., "Ascensio recta Solis, stellæ, aut alterius cujusdam signi, est gradus æquatorus cum quo simul exoritur in sphæra recta"; roughly translated, "Right ascension of the Sun, stars, or any other sign, is the degree of the equator that rises together in a right sphere"
- Lathrop, John (1821). A Compendious Treatise on the Use of Globes and Maps. Wells and Lilly and J.W. Burditt, Boston. pp. 29, 39.
- Moulton, Forest Ray (1916). An Introduction to Astronomy. Macmillan Co., New York. pp. 125–126.
- Moulton (1916), p. 126.
- Explanatory Supplement (1992), p. 11.
- Moulton (1916), pp. 92–95.
- see, for instance, U.S. Naval Observatory Nautical Almanac Office; U.K. Hydrographic Office; H.M. Nautical Almanac Office (2008). "Time Scales and Coordinate Systems, 2010". The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. B2.
- Blaeu (1668), p. 40–41.
External links
- MEASURING THE SKY A Quick Guide to the Celestial Sphere James B. Kaler, University of Illinois
- Celestial Equatorial Coordinate System University of Nebraska-Lincoln
- Celestial Equatorial Coordinate Explorers University of Nebraska-Lincoln
- Merrifield, Michael. "(α,δ) – Right Ascension & Declination". Sixty Symbols. Brady Haran for the University of Nottingham.
- Sidereal pointer (Torquetum) – to determine RA/DEC.