| Revision as of 17:28, 17 March 2010 editWatashinowiki (talk | contribs)8 edits →External links← Previous edit | Latest revision as of 05:10, 22 December 2024 edit undoJohsmithson (talk | contribs)2 edits Added contextTags: Mobile edit Mobile web edit | ||
| (74 intermediate revisions by 47 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Options trading strategy}} | |||
| ] | |||
| ] | ] | ||
| ] | |||
| ⚫ | In ], a butterfly is a limited risk, non-directional ] that is designed to have a |
||
| ⚫ | In ], a '''butterfly''' (or simply '''fly''') is a limited risk, non-directional ] that is designed to have a high ] of earning a limited profit when the future ] of the underlying asset is expected to be lower (when long the butterfly) or less lower (when short the butterfly) than that asset's current ]. | ||
| == Long butterfly == | == Long butterfly == | ||
| A ] butterfly position will make profit if the future volatility is lower than the implied volatility. | A ] butterfly position will make profit if the future volatility is lower than the implied volatility. | ||
| A long butterfly options strategy consists of the following ]: | A long butterfly options strategy consists of the following ]: | ||
| * ] 1 ] with a ] of (X − a) | * ] 1 ] with a ] of (X − a) | ||
| * ] 2 calls with a strike price of X | * ] 2 calls with a strike price of X | ||
| * Long 1 call with a strike price of (X + a) | * Long 1 call with a strike price of (X + a) | ||
| where X = the spot price (i.e. current market price of underlying) and a > 0. | |||
| where a > 0. | |||
| Using ] a long butterfly can also be created as follows: | Using ] a long butterfly can also be created as follows: | ||
| Line 19: | Line 19: | ||
| * Short 2 puts with a strike price of X | * Short 2 puts with a strike price of X | ||
| * Long 1 put with a strike price of (X − a) | * Long 1 put with a strike price of (X − a) | ||
| where a > 0 | where X = the spot price and a > 0. | ||
| All the options |
All the options have the same ] date. | ||
| At expiration the value (but not the profit) of the butterfly will be: | At expiration the value (but not the profit) of the butterfly will be: | ||
| * zero if the price of the underlying is below (X − a) or above (X + a) | * zero if the price of the underlying is below (X − a) or above (X + a) | ||
| * positive if the price of the underlying is between (X - a) and (X + a) |
* positive if the price of the underlying is between (X - a) and (X + a) | ||
| The maximum value occurs at X (see diagram). | The maximum value occurs at X (see diagram). | ||
| Line 31: | Line 31: | ||
| == Short butterfly == | == Short butterfly == | ||
| A ] butterfly position will make profit if the future volatility is higher than the implied volatility. | A ] butterfly position will make profit if the future volatility is higher than the implied volatility. | ||
| A short butterfly options strategy consists of the same options as a long butterfly. However |
A short butterfly options strategy consists of the same options as a long butterfly. However now the middle strike option position is a long position and the upper and lower strike option positions are short. | ||
| == |
== Margin requirements == | ||
| In the United States, margin requirements for all options positions, including a butterfly, are governed by what is known as ]. However brokers are permitted to apply more stringent margin requirements than the regulations. | |||
| ⚫ | |||
| ⚫ | The double option position in the middle is called the body, while the two other positions are called the wings. | ||
| == Use in calculating implied distributions == | |||
| ⚫ | The option strategy where the middle |
||
| The price of a butterfly centered around some strike price can be used to estimate the implied probability of the underlying being at that strike price at expiry. This means the set of market prices for butterflies centered around different strike prices can be used to infer the market's belief about the probability distribution for the underlying price at expiry. This implied distribution may be different from the ] assumed in the popular ], and studying it can reveal ways in which real-world assets differ from the idealized assets described by Black-Scholes.<ref name="Natenberg chapter 24">{{cite book |last1=Natenberg |first1=Sheldon |title=Option volatility and pricing: advanced trading strategies and techniques |date=2015 |location=New York |isbn=9780071818780 |edition=Second |chapter=Chapter 24}}</ref> | |||
| In an unbalanced butterfly the variable "a" has two different values. | |||
| == Butterfly variations == | |||
| ⚫ | |||
| ⚫ | #The double option position in the middle is called the body, while the two other positions are called the wings. | ||
| #In case the distance between middle strike price and strikes above and below is unequal, such position is referred to as "broken wings" butterfly (or "broken fly" for short). | |||
| # An ] recreates the payoff diagram of a butterfly, but with a combination of two calls and two puts. | |||
| ⚫ | # The option strategy where the middle options (the body) have different strike prices is known as a ]. | ||
| # A Christmas tree butterfly (not to be confused with the ]) consists of six options used to create a payoff diagram similar to a butterfly but slightly ] or ] instead of directionally neutral.<ref>{{cite web |title=Christmas Tree Butterfly Call |url=https://www.optionsplaybook.com/option-strategies/christmas-tree-butterfly-call/ |website=www.optionsplaybook.com |access-date=19 March 2022}}</ref><ref>{{cite web |title=Christmas Tree Butterfly Put |url=https://www.optionsplaybook.com/option-strategies/christmas-tree-butterfly-put/ |website=www.optionsplaybook.com |access-date=19 March 2022}}</ref> | |||
| ==References== | ==References== | ||
| {{reflist}} | |||
| * {{cite book | * {{cite book | ||
| | last = McMillan| first = Lawrence G. | | last = McMillan| first = Lawrence G. | ||
| | title = Options as a Strategic Investment | | title = Options as a Strategic Investment | ||
| | edition = 4th |
| edition = 4th | ||
| | publisher = New York : New York Institute of Finance | | publisher = New York : New York Institute of Finance | ||
| | year = 2002 | | year = 2002 | ||
| | isbn = 0-7352-0197-8 | | isbn = 0-7352-0197-8 | ||
| }} | }} | ||
| * {{Citation | |||
| |year=1986 | |||
| ==External links== | |||
| |title=Credit By Brokers And Dealers (Regulation T) | |||
| |publisher=FINRA | |||
| * graphically illustrates component options in long and short butterflies. | |||
| |url=http://www.ecfr.gov/cgi-bin/text-idx?tpl\=/ecfrbrowse/Title12/12cfr220_main_02.tpl | |||
| }} | |||
| * things you should know about Butterfly Spreads | |||
| * How to construct a Butterfly Option Spread- A real trade example on SPY | |||
| {{Derivatives market}} | {{Derivatives market}} | ||
| ] | ] | ||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 05:10, 22 December 2024
Options trading strategy
In finance, a butterfly (or simply fly) is a limited risk, non-directional options strategy that is designed to have a high probability of earning a limited profit when the future volatility of the underlying asset is expected to be lower (when long the butterfly) or less lower (when short the butterfly) than that asset's current implied volatility.
Long butterfly
A long butterfly position will make profit if the future volatility is lower than the implied volatility.
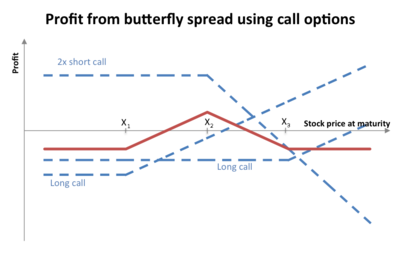
A long butterfly options strategy consists of the following options:
- Long 1 call with a strike price of (X − a)
- Short 2 calls with a strike price of X
- Long 1 call with a strike price of (X + a)
where X = the spot price (i.e. current market price of underlying) and a > 0.
Using put–call parity a long butterfly can also be created as follows:
- Long 1 put with a strike price of (X + a)
- Short 2 puts with a strike price of X
- Long 1 put with a strike price of (X − a)
where X = the spot price and a > 0.
All the options have the same expiration date.
At expiration the value (but not the profit) of the butterfly will be:
- zero if the price of the underlying is below (X − a) or above (X + a)
- positive if the price of the underlying is between (X - a) and (X + a)
The maximum value occurs at X (see diagram).
Short butterfly
A short butterfly position will make profit if the future volatility is higher than the implied volatility.
A short butterfly options strategy consists of the same options as a long butterfly. However now the middle strike option position is a long position and the upper and lower strike option positions are short.
Margin requirements
In the United States, margin requirements for all options positions, including a butterfly, are governed by what is known as Regulation T. However brokers are permitted to apply more stringent margin requirements than the regulations.
Use in calculating implied distributions
The price of a butterfly centered around some strike price can be used to estimate the implied probability of the underlying being at that strike price at expiry. This means the set of market prices for butterflies centered around different strike prices can be used to infer the market's belief about the probability distribution for the underlying price at expiry. This implied distribution may be different from the lognormal distribution assumed in the popular Black-Scholes model, and studying it can reveal ways in which real-world assets differ from the idealized assets described by Black-Scholes.
Butterfly variations
- The double option position in the middle is called the body, while the two other positions are called the wings.
- In case the distance between middle strike price and strikes above and below is unequal, such position is referred to as "broken wings" butterfly (or "broken fly" for short).
- An iron butterfly recreates the payoff diagram of a butterfly, but with a combination of two calls and two puts.
- The option strategy where the middle options (the body) have different strike prices is known as a Condor.
- A Christmas tree butterfly (not to be confused with the unrelated option combination also called a Christmas tree) consists of six options used to create a payoff diagram similar to a butterfly but slightly bearish or bullish instead of directionally neutral.
References
- Natenberg, Sheldon (2015). "Chapter 24". Option volatility and pricing: advanced trading strategies and techniques (Second ed.). New York. ISBN 9780071818780.
{{cite book}}: CS1 maint: location missing publisher (link) - "Christmas Tree Butterfly Call". www.optionsplaybook.com. Retrieved 19 March 2022.
- "Christmas Tree Butterfly Put". www.optionsplaybook.com. Retrieved 19 March 2022.
- McMillan, Lawrence G. (2002). Options as a Strategic Investment (4th ed.). New York : New York Institute of Finance. ISBN 0-7352-0197-8.
- Credit By Brokers And Dealers (Regulation T), FINRA, 1986