| Revision as of 07:57, 28 April 2008 editFDT (talk | contribs)7,708 edits Opinion on the two new articles← Previous edit | Revision as of 08:04, 28 April 2008 edit undoFDT (talk | contribs)7,708 edits Reply to PeR's warningNext edit → | ||
| Line 888: | Line 888: | ||
| Clearly there is team vandalism going on at present on this article. It is now in a worse state than when the edit war began. ] (]) 07:57, 28 April 2008 (UTC) | Clearly there is team vandalism going on at present on this article. It is now in a worse state than when the edit war began. ] (]) 07:57, 28 April 2008 (UTC) | ||
| == Reply to PeR == | |||
| PeR, there is no need to leave formal warnings for me in my tray. You have accused me of wikistalking. That is very rich coming from you. It's a case of the pot calling the kettle black. | |||
| You and FyzixFighter have been actively making a point of deleteing every single edit that I make. I am trying to improve this article. I tried to generalize the definition of centrifugal force but both of you reverted it to a high school version that shies away from anything more complicated than a circle. | |||
| That is wikistalking if ever there was a case. You are simply making that statement that you will let Wolfkeeper and Rracecarr edit these pages but under no account are you going to alow me to have the slightest input. That is wikistalking. | |||
| So do you want to call a truce, or do you want the administration to be brought in? ] (]) 08:04, 28 April 2008 (UTC) | |||
Revision as of 08:04, 28 April 2008
| Physics Redirect‑class High‑importance | ||||||||||
| ||||||||||
|
Archives |
The centrifuge
Does the centrifugal force that causes stuff to move to the outer edge of a centrifuge come under the real or fictitious category? If it is real, it is certainly not a reactive force. If it is fictitious, it has got a very real effect.
I suggest that the introduction be tidied up such as to define centrifugal force without splitting it into a real kind and a fictitious kind. 203.115.188.254 (talk) 11:01, 4 April 2008 (UTC)
- There happen to be two competing (and incompatible) uses of the term, and lack of perception of the differences continues to cause many confusions and even disputes in academia. Thus, how do you propose to do such "cleaning up" without recreating the kind of confusion that this article gets rid of from the start?
- About your example: There is no real direct force that causes stuff to move to the outer edge; such a hypothetical force can have no real effect. However, moving objects resist changing their trajectory, and that causes a very real reactive force against the centrifuge wall. Do you think that it may be useful to add this example? Harald88 (talk) 16:19, 6 April 2008 (UTC)
Harald88, In planetary orbital theory, an elliptical orbit is the result of an inward radial force of gravity and a very real outward radial force which is the centrifugal force.
In the centrifuge, gravity is neglible and so we only have the centrifugal force.
The orbital solution to a centrifugal force acting in isolation without gravity is an infinitely eccentric hyperbola. This translates into a straight line in the laboratory.
In the centrifuge, a very real effect occurs, but you say that this is simply due to the tendency of moving objects to resist changing their trajectory. This tendency is known as inertia and it is equivalent to centrifugal force in the laboratory. It is a very real effect.
Hence, I do not accept that centrifugal force is a fictitious effect. If it can bring about a real effect in a centrifuge, then it is real. David Tombe (talk) 07:29, 16 April 2008 (UTC)
- You did not answer my question. Do you think that it may be useful to add this example? Harald88 (talk) 09:21, 20 April 2008 (UTC)
Harald88, By all means put in a section about the centrifuge. It totally undermines the existing introduction which tries to claim that centrifugal force applies to two different things, one real and one fictitious, which just happen to act in the same place at the same time.
In the centrifuge, would they try to argue that the centrifugal force only becomes real at the moment when the heavy particles hit the edge?
That would be the same as saying that gravity for a man falling over a cliff only becomes real when he hits the ground. David Tombe (talk) 13:28, 21 April 2008 (UTC)
Is it real or fictitious?
The main article seems to be hedging its bets. It claims that there are two kinds of centrifugal force, with one kind being real and the other kind being fictitious. It then gives examples of each kind but goes on to admit that both of these kinds are the same thing.
The problem seems to be that modern literature presents centrifugal force to be a fictitious force, whereas classical literature presents it as a real force.
Even in the absence of a resolution of this controversy, the main article needs to be tidied up. We need to explain what centrifugal force is, without mentioning whether it is real or fictitious.
There then needs to be sections giving reasons for suggesting that it is fictitious, and sections giving reasons for suggesting that it is real.
But in its current form, the article is unsatisfactory because it talks of two kinds of centrifugal force when in fact there is only one kind. David Tombe (talk) 05:45, 18 April 2008 (UTC)
- No, the two uses are entirely incompatible, and I thought that the article makes that clear - one of the purposes of this article is to end such confusion and misjudgment. Where did you get that idea, which sentence needs to be improved?
- Note also that the article refers to a modern encyclopdia (edition of 2007) that defines centrifugal force as a reaction force.
- Thanks, Harald88 (talk) 09:19, 20 April 2008 (UTC)
- Harald88, the example of the swerving car in the so-called consensus version totally undermines what you have just said. It is trying to make out that the fictitious centrifugal force and the real centrifugal force are the same thing depending on how you view it.
- The version which I put in, which you didn't see because it was changed by Thermochap, merely states the facts as regards what centrifugal force is. It then points out that it used to be regarded as real, but that it is now regarded as fictitious. If you say that a 2007 encyclopaedia states that it is real, then that is a clear sign that there is no consensus on the matter within the physics community. David Tombe (talk) 12:31, 20 April 2008 (UTC)
The Introduction
Thermochap, I thought that the middle paragraph of your new introduction was unnecessarily complicated. It involved the Affine connection. Overall, I'm not happy with it because you have acknowledged that centrifugal force is a real reaction to a centripetal force and then brushed that fact under the carpet as being history. What do you call that real reaction effect now if it is no longer considered to be centrifugal force?
Meanwhile, you have emphasized the modern view that centrifugal force is only a fictitious effect as viewed from a rotating frame of reference, when in fact you are perfectly aware yourself that the effect is real.
I had deliberately worded the article in such as way as to point out that nowadays, centrifugal force is considered to be fictitious, whereas in days of old, it was considered to be real.David Tombe (talk) 08:14, 20 April 2008 (UTC)
- David, we have been through all this long ago. It is clear to everybody that you don't understand the first thing about this article's subject. Please do not try to edit it, your attempts to do so invariably make the article wrong and completely out of tune with established physical understanding. I have reverted it. –Henning Makholm 08:19, 20 April 2008 (UTC)
- Indeed, the use of the term as reaction force is less common nowadays, but that "old" meaning is related to Newtonian mechanics which led to the derivation of centripetal acceleration; which in turn is necessary for understanding the fictitious use of the term. Thus, although at a time I went along with putting the fictitious meaning first because of its greater popularity, for a logical and comprehensible explanation to the reader it is certainly better as it is now.
- In spite of that, as long as people like David turn up, it appears that it is still not well enough explained - or perhaps the topic is just to difficult? I'm not sure. David, what should be changed so that you won't find it confusing anymore?
- Thanks, Harald88 (talk) 09:14, 20 April 2008 (UTC)
- I actually think that the introduction is better off without any reference to the archaic use of the term "centrifucal force" to denote the reaction force to a centripetal force. That could still be in the article, but somewhere nearer the end. I also think that it needs to be made clear early in the article that the term "fictitious force" has a very specific meaning. It is not the same as "fictional". It is not the opposite of "real". It is a force that enters the calculations when a non-inertial reference frame is used. --PeR (talk) 17:28, 20 April 2008 (UTC)
- I agree with these points, mostly. However, we should be careful not to move the reaction force so far down that it appears to be merely a historical curiosity that can safely be skipped. That's what it is, of course, to one who groks the fictitious force, but it seems to me that regrettably often people confuse the two forces. Therefore readers deserves to have the difference between them explained in some detail. And it is far nicer to do that by saying, "here is an older meaning of the word, but beware that it is different from the mainstream meaning in such-and-such way", than to have to say "here is a stupid misconception that you must disabuse yourself of". Of course we can only do this because we have sources to show that the achaic sense of the term is not complete fuction -- but given that we do have those, grabbing the chance sounds like a good idea. –Henning Makholm 22:25, 20 April 2008 (UTC)
- Actually, because the reaction force is precisely a historical curiosity that can safely be skipped, I think it does more harm than good to give it a prominent position. Lots of people just read the first paragraph, and they should get as good info as possible. We should keep the text as clear as possible, and keep distractions to a minimum. --PeR (talk) 20:49, 21 April 2008 (UTC)
The Consensus Version
Henning, In the so-called consensus version, you talk about two kinds of centrifugal force. You talk about a real kind, and then you talk about a fictitious kind.
Below that, you then describe a scenario in which centrifugal force is either real or fictitious according to how you look at it.
This is entirely unsatisfactory.
The version which you reverted was not mine. In the version which I put in yesterday, I merely described centrifugal force and then pointed out the fact that it used to be considered to be real, but that nowadays it is considered to be fictitious.David Tombe (talk) 12:35, 20 April 2008 (UTC)
- No. The consensus version describes that the term "centrifugal force" has two different possible meanings, and then goes on to describe a situation that happen to illustrate both meanings. But even in the described situation the two meanings of "centrifugal force" refers to two different forces. –Henning Makholm 22:11, 20 April 2008 (UTC)
- David, The centrifugal force was never considered to be real by Newton, Maxwell, or Bernoulli. If you want to put a statement like that you need to cite a source. Specifically you need to cite a source that says "the centrifugal force was considered to be real", or something very similar to that. If you read a text by, say Maxwell, and interpret that as him saying that the centrifugal force is real, that is still original research, since it is your interpretation of what he says. --PeR (talk) 17:16, 20 April 2008 (UTC)
Thermochap pointed out this nice animation from commons:
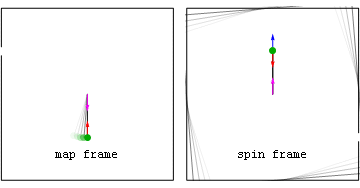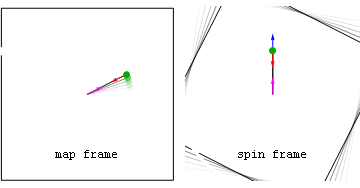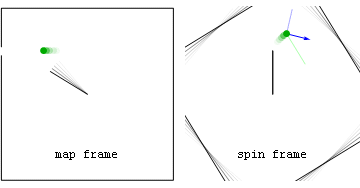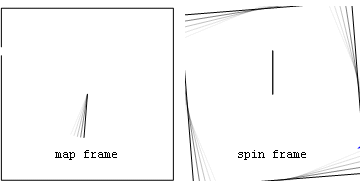
which nicely shows the difference between the two meanings described in the article. The red arrow is the centripetal force; the magenta one is the reactive centrifugal force, and the blue one is the fictitious force. I think this would make a good illustration for this article, if only the blue arrow had been decomposed into centrifugal and Coriolis terms after the green ball is let go. Names, aside, the force shown in magenta is and always was considered to be real; that shown in blue is and always was considered to be fictitious. –Henning Makholm 22:45, 20 April 2008 (UTC)
- Henning, centrifugal force has only one meaning. The controversy lies in whether or not it is real or fictitious. The official position today is that it is fictitious. However, in former times, it was considered to be real.
- I don't quite follow PeR's logic that if I were to provide a quote from an old paper confirming that centrifugal force was believed to be real, that this would have to be dismissed on the grounds that it was my original research.
- The present introduction is totally unsatisfactory because it is trying to fudge the controversy by stating that the term centrifugal force has two different possible meanings.
- The new introduction which I put in yesterday simply stated what centrifugal force is, and then further stated that the modern consensus is that centrifugal force is fictitious, whereas previously it had been regarded as real.David Tombe (talk) 07:11, 21 April 2008 (UTC)
- If you don't understand what I said, then read WP:OR. Then read what I said again. I'm tired of repeating myself. --PeR (talk) 07:57, 21 April 2008 (UTC)
Admissibility of Evidence
PeR, I think that you are going to have to repeat yourself. We need to get something straight here regarding the issue of admissibility of evidence. You declared that centrifugal force was never considered to be real. You further went on to state that if I were to produce any quotes from Newton or Bernoulli which indicated that they believed that centrifugal force was real, that this would not be deemed to be admissible evidence on the grounds that it would be my own original research.
Here is a quote from Bernoulli out of the ET Whittaker book on the history of aethers.
"The elasticity which the Aether appears to possess, and in virtue of which it is able to transmit vibrations, is really due to the presence of these whirlpools; for, owing to centrifugal force, each whirlpool is continually striving to dilate, and so presses against the neighbouring whirlpools."
And here is a quote from Maxwell's paper 'On Physical Lines of Force',
"The explanation which most readily occurs to the mind is that the excess of pressure in the equatorial direction arises from the centrifugal force of vortices or eddies in the medium having their axes in directions parallel to the lines of force"
And you are trying to tell me that this is not evidence to suggest that Bernoulli and Maxwell believed that centrifugal force was real?
- YES! I am trying to tell you that this is not evidence to suggest that Bernoulli and Maxwell believed that centrifugal force was real. However, if you don't want to accept this you don't have to. Just don't write anything in the article. If you do want to write something like that then you must (and here I am repeating myself, as requested) cite a source that says "the centrifugal force was considered to be real" or something very similar to that. If you read a text by, say Maxwell, and interpret that as him saying that the centrifugal force is real, that is still original research, since it is your interpretation of what he says. --PeR (talk) 19:42, 21 April 2008 (UTC)
PeR, There is a controversy about whether or not centrifugal force is real. The official position today is that it is not real.
The current introduction is abominable because it tries to fudge the issue by pretending that there are two centrifugal forces. One for the realists, and one for the fictitiousists. This is an extreme case of ecclecticism. The current introduction cannot remain because it is a total disgrace.David Tombe (talk) 08:02, 21 April 2008 (UTC)
- You misinterpret what it says. However, the fact that you don't understand it is evidence that it is not clearly enough written, so I agree that it should be rewritten. --PeR (talk) 19:42, 21 April 2008 (UTC)
Suggestions for improved and simplified introduction
PeR, I'm glad that you agree that the introduction should be re-written. So let's take it one step at a time.
First of all, I assume that we are both agreed that somewhere in the introduction there should be a statement clarifying that we should not be confusing centrifugal force with centripetal force.
And now, how about this for an introductory sentence?
"When an object is constrained to move in circular motion, an outward radial force will be observed to act on that object"
Would you agree that that is a correct statement of fact? There is certainly no need to distinguish between the reactive kind and the other kind because they are exactly the same effect.
Beyond that, I can't think that much more is needed in the introduction other than to state that a controversy exists regarding whether or not it is real or fictitious. David Tombe (talk) 02:13, 22 April 2008 (UTC)
- Your proposal is not a correct statement of fact. It is simply false. An outward centrifugal force appears to act on an object only when it is described in a rotating coordinate system - and then not just for objects moving in circles, but for all object that are observed in that coordinate system. The outwards force that appears in an inertial system when an object moves in a circle does not act on the object that moves circularly, but on the constraints that make it move in a circle. This is clearly described in the article (at least when you have not recently vandalised it), and there are several descriptions of it to be found on this talk page.
- Your continued assertions that these two forces are the same force are simply wrong. The two forces do not even apply to the same body. There is no controversy whatsoever about whether any of these forces are real or fictitious. Everybody agrees that the reactive force is (usually) real; and everybody agrees that the fictitious force is fictitious. Nothing of this will change because you continue to claim that it is false. –Henning Makholm 04:11, 22 April 2008 (UTC)
Henning, you are making it more complicated that it is. When an object is constrained to move in a circle, then an outward centrifugal force will act on it.
And there is a controversy about whether centrifugal force is real or fictitious. And there is only one centrifugal force. It is sheer double talk to split centrifugal force into two in order to cater for both beliefs. David Tombe (talk) 04:44, 22 April 2008 (UTC)
- David, read what Henning wrote again. Your proposal is not a correct statement of fact. It is simply false. --PeR (talk) 07:04, 22 April 2008 (UTC)
PeR, OK, let's go through Henning Makholm's reply stage by stage. He says,
An outward centrifugal force appears to act on an object only when it is described in a rotating coordinate system
The very fact that we state the word 'outward' describes the effect perfectly without having to mention anything about rotating coordinate systems. Henning Makholm is making it more complicated than it is.
He then states,
- and then not just for objects moving in circles, but for all object that are observed in that coordinate system.
This statement was totally unnecessary because all objects that are observed in that coordinate system will be partaking in the circular motion in question. This was just a clouding statement.
- Utter nonsense. Our choice to describe things from a rotating coordinate system cannot possibly make things move circularly. There is an infinitude of possible kinds of movements that are circular in neither an inertial coordinate system nor in a rotating one. –Henning Makholm 19:50, 22 April 2008 (UTC)
- Henning, my apologies. I should have clarified that all objects that experience centrifugal force in that coordinate system will be partaking in the circular motion in question. We don't need to mention rotating frames. It is only necessary that an object be constrained to follow a curved path. David Tombe (talk) 05:38, 23 April 2008 (UTC)
He then states,
The outwards force that appears in an inertial system when an object moves in a circle does not act on the object that moves circularly, but on the constraints that make it move in a circle.
What happens in a centrifuge regarding the large particles before they reach the edge? Is the centrifugal force not acting on them?
- When viewed from an inertial coordinate system, there is no centrifugal force acting on particles. Before they reach the edge, they drift with constant velocity within the centrifuge. When viewed from a co-rotating system, a centrifugal force acts on particles as they drift towards the edge, and keeps acting to pin them to the wall. In both cases the particles will start pushing the wall outwards once they stick to the wall (this is the reactive meaning of the centrifugal force). –Henning Makholm 19:50, 22 April 2008 (UTC)
- Henning, Yes there is. These particles have been constrained to partake in the circular motion, and a centrifugal force acts radially outwards on them and causes them to accelerate towards the edge. If they were not constrained to move circularly with the centrifuge, then no centrifugal force would act on them. The centrifugal force is an absolute radial effect.David Tombe (talk) 06:03, 23 April 2008 (UTC)
He then says,
Your continued assertions that these two forces are the same force are simply wrong. The two forces do not even apply to the same body.
It's only in Henning Makholm's imagination that there are two centrifugal forces. No textbook ever states such a notion.
- Perhaps not. But there are sufficient citations for either of the two different notions, and they are clearly two different notions, sharing essentially nothing but the name. –Henning Makholm 19:50, 22 April 2008 (UTC)
As for Henning Makholm's claim that the two forces don't even apply to the same body, he is only making the matter worse. In the example in the introduction to the main article, the bit that you call the fictitious centrifugal force acts to throw the man towards the car door. The bit which you call the reactive centrifugal force occurs by virtue of the man pushing against the car door as a result of that very same centrifugal force.
- In this example, the fictitious centrifugal force applies to the passenger. The reactive centrifugal force applies to the car door. That is two different forces, and arguments about one causing the other does not make them into the same force. –Henning Makholm 19:50, 22 April 2008 (UTC)
- Henning, it's a transmission of the same effect. It is splitting hairs to divide it into two different forces. That can all be discussed in the main article. There is no need to mention the reactive effect in the introduction.David Tombe (talk) 06:03, 23 April 2008 (UTC)
And he is saying that these two centrifugal forces do not act on the same body. It's like saying that the force with which a man hits the ground is not the same force as the gravity which caused him to fall over the cliff.
- Of course they are not. The gravity applies to the man and causes him to accelerate downwards. Later, contact forces apply to the dirt where the man hits and cause the dirt to be rearranged. They are not the same force -- not only do they act on different bodies, they act at different times. Gravity acts continuously during the fall; the contact forces act only during the collision. –Henning Makholm 19:50, 22 April 2008 (UTC)
- Henning, No. Even when the object is lying at rest on the Earth, gravity is still pushing it against the Earth. David Tombe (talk) 06:03, 23 April 2008 (UTC)
The man pushes against the car door because of the one and only centrifugal force.
- From an inertial viewpoint, the man pushes against the car door because the car door pushes against the man, trying to make him turn a corner. In any case the reason why the man pushes is not the same as the force against the door that the pushing constitutes. –Henning Makholm 19:50, 22 April 2008 (UTC)
I need to have a citation which specifically states that centrifugal force applies to two different forces. David Tombe (talk) 08:04, 22 April 2008 (UTC)
- I agree with your last statement. We need to cite a science-history book that states that Newton and others used the word "centrifugal force" with a different meaning than that which is used today. (The current references only show the usage of the term, which is not the same thing.) The rest of your analysis is just plain wrong. Sorry. My best advice is that you try reading the fictitious force article, some elementary mechanics textbooks, and then try reading Hennings text again. --PeR (talk) 10:00, 22 April 2008 (UTC)
- What we seem to need is citations for the ordinary, fictitious, meaning of "centrifugal force". Once both meanings are properly cited to be (have been) in use, there will be no need to cite separately the obvious fact that the two meanings are different. –Henning Makholm 19:50, 22 April 2008 (UTC)~
Henning, That is not good enough. We know that there is centrifugal force. And we know that there are references that apply it to the reaction against the force that constrains the object to the curved path. But that is not sufficient to justify an unconventional claim that centrifugal force is a term which applies to two different forces. Such a claim is a grossly misleading exaggeration of the truth. David Tombe (talk) 06:03, 23 April 2008 (UTC)
PeR, so far your entire contribution to this debate has been to state that I am wrong and that I should read more of what Henning Makholm has to say, as if by reading his nonsense over and over again, then I might actually believe it eventually.
I'd like to hear your own analysis of the situation.
Let's go back to the very beginning. Tell me at what point this basic sentence goes wrong,
The centrifugal force is an outward radial force that acts on any object that is constrained to move in circular motion.David Tombe (talk) 13:32, 22 April 2008 (UTC)
- Your statement doesn't properly describe the fictitious force (modern use of the term "centrifugal force"), because it fails to mention the rotating reference frame. It doesn't describe the reaction force (Newton's use of the term), because it says that it acts on the object itself, not the thing which is constraining it to move in a circle. --PeR (talk) 13:53, 22 April 2008 (UTC)
PeR, the fact that the object is constrained to move in circular motion caters for the rotating frame of reference aspect. As for the reaction bit, that can be dealt with in the main body of the article. That is an extension of the concept. A body which is being acted upon by a centrifugal force naturally transmits this force on when it comes into contact with another body. —Preceding unsigned comment added by David Tombe (talk • contribs) 14:38, 22 April 2008 (UTC)
- This is utterly wrong. The choice of which reference frame to use (and hence whether or not one must consider a fictitious centrifugal force) can be made independently of how things move. Some choices may be more or less convenient according to whether they simply the movements, but the actual movements cannot make any choice of reference frame more or less correct. –Henning Makholm 19:50, 22 April 2008 (UTC)
The reasons for the reversion of the wikified version
The wikified version is teaching the false doctrine that centrifugal force is a term which applies to two different forces.
This doctrine is based on the idea that the centrifugal force which throws the passenger towards the door of the swerving car is a different force from the force which the passenger eventually causes on the door when contact is made.
The argument goes that a fictitious force throws the passenger to the car door and when contact is made, this is then transmitted into a real force which pushes against the door.
Such an argument is the same as saying that the force which an object causes on the Earth's surface due to its weight is a different force from the gravitional force that pushes the person against the surface of the Earth.
There is one force of gravity, and there is one centrifugal force.
The introduction to the article must describe in as simple terms as possible what that one centrifugal force is.David Tombe (talk) 13:47, 22 April 2008 (UTC)
- I don't know whether what you say is true or not, but please IF you are going to rewrite the article, rewrite it in such a way that the article is wikified! Stephenb (Talk) 15:01, 22 April 2008 (UTC)
- Looking at both versions of the text, I have to say it looks as though reverting was correct, but I'm no physicist. Have you guys thought of trying Misplaced Pages:Third opinion and getting another opinion? Stephenb (Talk) 15:29, 22 April 2008 (UTC)~
- Stephen, thanks for replying. But I can assure you that the onus of wikification is on them. They need to provide a citation which clearly states that centrifugal force is a term which applies to two different forces. There is no textbook or encyclopaedia which will state that. David Tombe (talk) 05:41, 23 April 2008 (UTC)
- You misunderstand. Wikification is the process of turning the text into an article, using proper grammar, formatting, references and citations. Whether or not your version or the other version contains faulty information is not why I reverted. The "consensus" version was wikified; yours was not, and looked like someone had edited it in bad faith resulting in a poor article, which is bordering on vandalism (since it appeared to remove information too). Stephenb (Talk) 09:10, 23 April 2008 (UTC)
In the old days, before about 1950, physics books called centrifugal force an inertial force. In those days inertial force was the term used for what today are labeled fictious forces. What this means is that the force is frame dependent. The force can be made to go away by simply switching from a noninertial frame to an inertial frame and the force disapears. The older terminology is certainly less of a problem, since students now wonder what is this fictious force? in my view the entire discussion of this is confusing and of questionable value as part of the article. There are no fictious forces, since they dont exist by definition of the word. So saying centrifugal force is fictious is the same as saying it doesnt exist. But since it does exist, that is bound to create confusion. I propose using the term frame dependent force since that captures the essential meaning of what is happening and we get rid of this textbook stupidity of fictious forces.Electrodynamicist (talk) 16:07, 22 April 2008 (UTC)
- It is definitely worth mentioning that "fictitious force" is synonymous to the older "inertial force". Indeed it is a poorly chosen term, but this is an encyclopedia, not a place for redefining terminology. If it were, there certainly wouldn't be an article entitled imaginary number. --PeR (talk) 18:21, 22 April 2008 (UTC)
- Update: Looking at some different uses of the term "inertial force" (including the Misplaced Pages disambig page inertial force) it seems the term has to meanings, in the same way as "centrifugal force" does. Thus, the sentence The centrifugal force is an inertial force. is correct in two ways (out of four :-). --PeR (talk) 09:50, 25 April 2008 (UTC)
Elliptical Motion
Henning, a rotating reference frame is irrelevant. The object in question has to actually be rotating with that reference frame before the centrifugal force will be induced. In other words, the object has to be constrained to move in circular motion.
There is no need to mention reference frames. In the swerving car scenario, the passenger is being constrained to follow the circular path by virtue of the back of his seat pushing him. A radially outward centrifugal force then occurs at right angles to this.
We must not lose track of the fact that this centrifugal effect is not something that is confined to circular motion. It occurs in any curved path motion. It occurs in elliptical and hyperbolic motion.
Therefore , mention of a rotating frame of reference merely confuses the issue because there could be an object which is stationary in the inertial frame. In the rotating frame, this object would trace out a circle, but it would experince no centrifugal force.
Regarding the 'reactive' centrifugal force, this is not a different force. It is an extension, or a transmission of the same effect. David Tombe (talk) 05:28, 23 April 2008 (UTC)
PeR
PeR, You have just reverted a perfectly good introduction to a shambles version. Did you even read what I said about elliptical motion? Anyway, a citation will be needed for the version which you have put in place.
We haven't even heard any evidence yet that you understand the issues in question. You seem to always just defer to what Henning Makholm says. The version which I put in was easier to read and it covered the key points. Nobody is disputing any fact which I wrote in that introduction. David Tombe (talk) 06:11, 23 April 2008 (UTC)
- David, you might want to read through this. Notice how everybody else (including me) is politely trying to explain why you're wrong? Notice how nobody agrees with you? Maybe you should consider the possibility that the others may be right? --PeR (talk) 08:24, 23 April 2008 (UTC)
PeR, You obviously haven't been paying the slightest bit of attention to anything that has been going on. Your mind is totally locked into last year's argument.
We are not arguing about whether the centrifugal force is real or fictitious. That was last year's argument and I still have my own opinion on that matter.
At the moment, we are trying to clean up the existing introduction in certain key respects. These are notably,
(1) To avoid any specific statement, especially in the first line of the introduction, to the extent that centrifugal force is a term which is applied to two different forces.
The reality is that one of those effects is a transmitted effect of the other. That can be dealt with in the main body of the article. There is no need to deal with that in the introduction.
(ii) We need to generalize the wording to cater for all kinds of curved path motion. In the so-called consensus version, one might get the impression that centrifugal force only occurs with circular motion.
So far, your only contribution to this debate has been to continually repeat that I am wrong without even being specific as to which particular point you are talking about. And you seem to have a habbit of referring what other people have said.
Can we soon maybe hear some of your own views, just so that we can be sure that you actually understand the issues in question.David Tombe (talk) 08:52, 23 April 2008 (UTC)
The Recent Edits
Rracecarr, The edits that you undid were designed to generalize the situation to cater for curved motion generally, which it seems that you began to realize after you had made the reversion.
They were also designed to treat reactive centrifugal force as a knock effect rather than as a distinct force in its own right.
The version which you reverted to contains some errors. Notably it doesn't specify that an object has to be co-rotating in a rotating frame in order to experience centrifugal force.
Surely you must know that already. Centrifugal force is treated in modern applied maths courses as one of two inertial effects which supplement the true acceleration when we do a rotating coordinate frame transformation. In order for the centrifugal force to be non-zero the object must have a tangential speed of zero relative to the rotating frame.
Ideally, I would like to see the introduction very much simplified and all matters to do with reactive centrifugal force dealt with in a section in the main article.David Tombe (talk) 15:30, 23 April 2008 (UTC)
Errors in the intro
There are at least 2 errors in the version being pushed by DT. 1) Centrifugal force is present in a rotating frame whether or not the object rotates with the frame; 2) the centrifugal force does not act away from the focus--this is sloppy terminology. For example, the centripetal force experienced by a particle moving along a parabolic path does not in general point toward the focus of the parabola.Rracecarr (talk) 15:30, 23 April 2008 (UTC)
- Rracecarr, Regarding point number (1), if an object is not co-rotating with a rotating frame, then it experiences no centrifugal force.
- Imagine you are standing on the ground. Above you is a large rotating disc. Somebody sitting on that rotating disc will consider that you are tracing out a circular path. Neither he nor you will observe any centrifugal force.
- You are getting confused with Coriolis force. Coriolis force is different because it is a tangential effect and a fictitious Coriolis effect can indeed be induced on an object which is moving, but not necessarily co-rotating with the frame. Centrifugal force is a radial force and it cannot be introduced as an artifact of rotation. But if somebody is constrained to co-rotate, then they will experience an outward radial centrifugal force.
- On point number (2), yes it was sloppy terminology but I wanted to get the point started that we are not confined to circular motion.
- What you should have done was improved the terminology. There was no need for a wholesale reversion. David Tombe (talk) 15:42, 23 April 2008 (UTC)
- You are flat wrong that there is no centrifugal force if the object does not rotate with the frame. The centrifugal force in a rotating frame of reference is totally independent of the velocity of the object. It depends only on the position, and is only zero if the object is collocated with the axis of rotation. I'm not going to revert right now because I'm already past 3RR (as are you--I think you're at 5). Rracecarr (talk) 16:18, 23 April 2008 (UTC)
No Rracecarr, it is you that is totally wrong. If an object is not rotating with the frame, it will be tracing out a circle in that frame. There will be no centrifugal force acting on it in any shape or form.
To get centrifugal force, we need to have a tangential speed measured relative to the true inertial frame. Co-rotation with a rotating frame is a perfect scenario.
When the car swerves around the corner, the seat of the car is constraining the passenger to co-rotate in the circle we the car is following. Hence a radial centrifugal force is induced which throws the passenger to the side door.
I can see that your confusion comes due to your special interest in Coriolis force. Fictitious Coriolis force has got important differences to centrifugal force.
Circular motion can induce tangential motion as an artifact. But it cannot induce radial motion as an artifact. Coriolis force is a tangential effect and centrifugal force is a radial effect.
In classical mecahnics, I'm sure you have done the equations. We end up with the two 'inertial terms'. One is Coriolis force. If we do a radial motion in the rotating frame, we will get an apparent tangential deflection as viewed from the rotating frame.
However, the centrifugal force term only becomes active if there is a tangential velocity as measured relative to the true frame. David Tombe (talk) 16:32, 23 April 2008 (UTC)
- This edit misses the point. Centrifugal force is a useful concept in rotating reference frames, and it acts on all objects, whether they're moving in a curved path, a straight path, or not moving at all. In my view you have removed the most important and useful definition. I'm not going to waste time arguing with you, because it is obvious that you won't listen. Fortunately, someone else who understands physics will likely be along soon to correct your mistakes. Otherwise I will revert tomorrow.Rracecarr (talk) 16:36, 23 April 2008 (UTC)
Rracecarr, the centrifugal force that I am talking about is the one that occurs in a centrifuge. As the heavy particles in the solution are constrained to co-rotate, they experience an outward radial force which moves them to the edge.
The centrifugal force that you are talking about is a mathematical game. It doesn't exist. There is a circular motion artifact. That is all.
But thanks to PeR's message on my talk page, I can now finally see where you are coming from. Somehow, you can see in this circular motion, a resultant between a Coriolis force and a centrifugal force.
If that is official teaching, then so be it. But in that case, we really need to be introducing three centrifugal forces into the main article.
(1) The real centrifugal force such as occurs in the centrifuge when particles get thrown to the edge, or when passengers get thrown to the side door when a car swerves around a corner.
(2) Then there is the knock on effect of this which some people describe as the reactive centrifugal force. When the object in (1) presses against something, due to the centrifugal force, it transmits the effect on to that something, just as a book on a table transmits the force of gravity unto the table in the form of its weight.
(3) And finally we have this ultra mathematical nicety which contributes towards an artificial circular path as viewed from a rotating frame of reference.
Finally I know what you are talking about. But quite frankly, when a reader wants to read about centrifugal force, they will only be interested in (1), and I think that it is (1) which the article should be concentrating on.
It seems that you, PeR, and Henning Makholm have been subtely pushing (3) and are determined to keep it that way. David Tombe (talk) 17:14, 23 April 2008 (UTC)
- Your (1) and (3) are the same thing. They are forces which appear when you view the world through a rotating frame of reference. It seems you would like to draw a distinction between the intuitive force (1) and the mathematical description of it (3). Rracecarr (talk) 17:46, 23 April 2008 (UTC)
Rracecarr, The only thing that viewing something from a rotating reference frame does is to introduce a circular motion artifact on top of the alreay existing motion. It does absolutely nothing else.
The centrifuge on the other hand produces a very real radial effect which is absolute, and can be viewed from any frame of reference.
So the fictitious effect which you are interested in is not the same thing as the centrifugal force as is commonly understood by the man in the street.
The man in the street sees centrifugal force as the outward radial force which occurs when an object is constrained to follow a curved path.
You are just playing out cheap mathematical games and confusing this whole article.
There is a big difference between an object that is co-rotating in a rotating reference frame and an object that is at rest in the inertial frame and viewed from the rotating frame. In the former, an actual centrifugal force accelerates the object radially outwards. In the latter, nothing happens.
If you can't see the difference between the two situations, then you are not living in the real world.
You, and PeR, and Henning Makholm are totally messing this article up to satisfy your own curiosity about irrelevent manipulations of maths.
You seem to think that there is something very interesting about the fact that the artificial circle can mathematically equate to the summation of the expression for Centrifugal force and the expression for Coriolis force.
At best, that is hardly interesting, and it's certainly not what a reader has in mind when he wants to read about centrifugal force.
But at any rate, the whole basis of this idea is faulty. Take a look at the mathematical expressions for the two fictitious forces. They both involve the angular velocity quantity ω. This angular velocity equates to v/r where v is the speed relative to the true frame.
In other words, these expressions only have any significance for objects moving at v relative to the true frame (ie. co-rotating with the rotating frame).
This can be easily demonstrated simply by looking at the centrifuge. If there is no co-rotation then the centrifuge will not operate.
This theory of yours, that a fictitious centrifugal force combines with a fictitious Coriolis force to yield a fictitious centripetal force is totally bogus.
And you are sacrificing this whole article in the name of this pet theory of yours. David Tombe (talk) 05:43, 24 April 2008 (UTC)
- I am going to try not to be snippety or condescending, in the hopes that you will listen rather than simply defend. Heavy things move toward the outside of a spinning centrifuge. This effect can be understood in 2 different ways: by analyzing in an inertial reference frame (the lab) or by analyzing in a frame which rotates with the centrifuge.
- In the lab frame, the stuff in the centrifuge spins in circles: it accelerates inward toward the middle of the centrifuge. A centripetal force is required to maintain this centripetal acceleration, and the heavier particles require more force, due to Newton's second law. Because it is "harder" to bend the paths of the heavier particles, they go "straighter" and move toward the outside. Intuitively, it seems there is a centrifugal force flinging them outward, but in the lab frame there really is no such force. If you write out the equations of motion, there is no term for centrifugal force--it exists only in people's imaginations.
- The second way of understanding the effect is by moving to the frame with rotates with the centrifuge. In that case, the stuff inside doesn't spin around at all--it basically sits still, but again, the heavier particles move toward the outside. In this frame, the movement is caused by a centrifugal force, which arises because of the rotating frame of reference. The centrifugal force exists in this frame, in the sense that there is a term for it in the equation of motion, but it is fictitious in the sense that it only exists because we've chosen a rotating frame of reference--there is still no actual physical source of outward force. Rracecarr (talk) 18:48, 24 April 2008 (UTC)
Rracecarr, Thank you for your response. I can understand why you think like that, but you are overlooking some points.
First, I should point out that I understand that wikipedia is about presenting the official viewpoint, and if my viewpoint differs from the official viewpoint, then I will not be attempting to impose my viewpoint on the main page.
The official viewpoint regarding the centrifugal force in the centrifuge is that it is an 'inertial' force, and as such, I will not be arguing with that fact on the main page.
At the moment, I am trying to get you to see that whether the centrifugal force in the centrifuge is 'inertial' or 'fictitious' or whatever, that it is quite different from the purely fictitious effect which is an artifact of a rotating frame of reference. In the latter case, a particle that is stationary in the true frame is not being subjected to any kinds of force whatsoever.
Now even if you wish to write off the centrifuge effect as being fictitious too, you must at least admit that it is nevertheless real enough to invoke Archimedes' principle.
That alone is sufficient grounds upon which to distinguish between the two scenarios.
Regarding my own opinions on what you said, I should state that in the laboratory Cartesian frame that centrifugal force is disguised as 'Inertia'. It is the straight line motion that is the extreme hyperbola asociated with a central force orbit in which the inward gravity force is zero.
The reality of the situation is that there is a radially outward force in circular motion, no matter from what frame of reference we view it.
But that is only my opinion and I will not enforce that on the main page. Nevertheless, I believe that if you stand back and take the broader view, you will realize that there is a point here.
What I am trying to correct on the main page is the presentation, coherence and emphasis.
I want the reactive centrifugal force to be discussed as a knock on effect in the main article. There are some good citations there, but it shouldn't be clouding the introduction.
I want the introduction to focus on the 'inertial' effect that occurs in a centrifuge or when a passenger gets flung to the side door of a swerving car. I want it to refer to the general case of curved path motion and not exclusively to circular motion.
I am opposed to the emphasis that is placed on the issue of rotating frames of reference as these are not needed to observe the effect.
I am opposed to the emphasis that is placed on the artificial circular motion. That is not centrifugal force. The theory that makes out that a fictitious centripetal force results from a fictitious centrifugal force and a fictitious Coriolis force is false on a number of counts.
(1)You cannot have a centripetal force in isolation. In the radial direction, it must be balanced by centrifugal force otherwise there would be radial motion.
- Yes, but radial motion can occur in general.- (User) WolfKeeper (Talk) 05:21, 25 April 2008 (UTC)
(2)Despite what some people say, the Coriolis force does not act radially. The entire derivation is based on the principle that it is a tangential force and so it cannot act along the same line as the centrifugal force. The two forces are always mutually perpendicular.
- Sorry, this is quite wrong. The Coriolis acceleration is: . As you can see, since it is a cross-product, if v is perpendicular to r then it acts completely radially.- (User) WolfKeeper (Talk) 05:21, 25 April 2008 (UTC)
(3)Those 'inertial' force equations are only designed to apply to objects that co-rotate. The angular velocity ω terms refer to the tangential velocity of the co-rotating object. For an object that is stationary in the true frame, those terms do not exist. David Tombe (talk) 04:31, 25 April 2008 (UTC)
- Sorry, but that is wrong also. Coriolis and Centrifugal acceleration/forces apply to all objects when considered from the rotating frame of reference. They do not have to be rotating in 'reality' (i.e. as seen from an inertial frame).- (User) WolfKeeper (Talk) 05:21, 25 April 2008 (UTC)
- Actually, if you consider the *lab* from Racecarr's above example with the centrifuge, the fictitious acceleration also acts on it! So how come it doesn't fly off? It's because the coriolis force holds the lab in a circular motion around the centrifuge, because the coriolis acceleration/force is purely radial in that case!- (User) WolfKeeper (Talk) 05:21, 25 April 2008 (UTC)
- Wolfkeeper, I was fully aware of the fact that the Coriolis acceleration is . But if you ever studied the derivation of this term, you would see that it is only the tangential component that we are interested in.
- No. The equation means what it says. omega is a vector aligned with the rotation axis which is of length proportional to the angular velocity, v is a vector that is aligned with the instantaneous velocity of a particle. 'x' is the cross product. There is no other valid interpretation of that equation; and it most definitely may point radially.- (User) WolfKeeper (Talk) 17:34, 25 April 2008 (UTC)
- Once again, you have become fixated on this ultra fictitious scenario regarding why the background stars don't fly off due to the Earth's diurnal rotation.
- No, not at all.- (User) WolfKeeper (Talk) 17:34, 25 April 2008 (UTC)
- The question I am trying to address is,
- can you see the difference between these two case scenarios?
- (a) A stationary object as viewed from a rotating frame of reference.
- (b) An object co-rotating with a rotating frame of reference hence inducing a radial centrifugal force which is real enough to invoke Archimedes' principle.
- Can you see the difference between those two scenarios? David Tombe (talk) 07:02, 25 April 2008 (UTC)
- You didn't answer my question (below). Explain your own theory properly, before you ask others why they think it's wrong. --PeR (talk) 07:51, 25 April 2008 (UTC)
PeR, you missed the point. This has got nothing to do with any theories of mine. I'm trying to focus your attention on the fact that swinging buckets of water over your head the not the same as the background stars describing circles across the sky.
Your team are fixated on the latter and all the mathematical games that you can play to try and argue that a stationary object has got a net summation of fictitious forces acting on it.
This article is supposed to be about the 'inertial' centrifugal force of the centrifuge.David Tombe (talk) 15:02, 25 April 2008 (UTC)
Reply to PeR
PeR, Regarding your private message to me, I should reply that you are not in a position to tell other people not to edit this page. Misplaced Pages is an ongoing thing. Since you didn't like my alternative version (although somebody else obviously did), I decided to fix up the existing version instead.
And you can discuss these matters on the talk page. You don't need to go private behind the scenes.
I now understand exactly where you, Henning Makholm and RRacecarr are going wrong. You can't see the difference between the situation which occurs when an object is co-rotating with a rotating reference frame, and when the object is not co-rotating.
It is only when the object is co-rotating that we get any actual effect. The situation that you like to highlight regarding the artificial circle, really is fictitious in the true sense of the word, and it is of no interest to anybody.
The situation which I am interested in is the inertial effect which occurs in a centrifuge.
In the introduction, we need to state the very basic and simple sentence that when an object is constrained to move in a curved path, it experiences a radially outward force.
The introduction cannot be allowed to focus on that obscure fictitious scenario that you seem to be so interested in, and indeed there is precious reason to even bother mentioning it in the main article.
You cannot dominate the topic with all that nonsense about a fictitious Coriolis force twice as strong as a fictitious centrifugal force causing a fictitious centripetal force. That is not what the readers are interested in.
Secondly, the reactive aspect shouldn't be in the introduction. It should be in a section in the main article.
The readers want the outward radial effect which comes from constrained curved motion. They want swinging buckets of water over the head. They want masses being swung around on the end of a string and discussions about whether they fly off radially tangentially or both, when released.
There is no need to mention rotating frames of reference because a centrifuge can be seen to have worked irrespective of which reference frame we view it from.
You are trying to cloud up this article with what you believe to be some clever realization about fictitious forces summing together to give other fictitious forces and you don't want to face up to what centrifugal force is really about. David Tombe (talk) 11:19, 24 April 2008 (UTC)
- Your talk page is not behind the scenes. Anyone can read it.
- Here's a part of what you wrote in the introduction:
- An inertial or "fictitious" centrifugal force appears when a rotating reference frame is used for analysis, providing that the object in question co-rotates with the frame. The true acceleration on objects that are co-rotating with the frame is supplemented by a radially outward (fictitious) centrifugal force.
- This effect can be extended generally to all curved path motions.
- Now tell me, with your "definition" of centrifugal force, when is an object considered to be co-rotating with the frame? When it is stationary in the frame, sure. But what if it has a very small, but nonzero velocity relative to the frame? What if this speed becomes slightly larger? What if the speed in the rotating frame is so large that the object is stationary in the inertial frame? In that case you say there is no centrifugal force. Where do you draw the limit? Does your centrifugal force end abruptly, or does it phase out as the velocity relative to the rotating frame increases? Mechanics is an exact science, so please give equations explaining your theory. Also, please give a reference to the textbook where you found that equation. --PeR (talk) 18:45, 24 April 2008 (UTC)
PeR, centrifugal force exists to the extent that the motion co-rotates. Ultimately the effect can be traced to the tangential velocity with respect to the rotation axis in the laboratory frame. David Tombe (talk) 04:34, 25 April 2008 (UTC)
- "to the extent that the motion co-rotates" is rather vague. Mechanics is an exact science, so please give equations with a refrence. --PeR (talk) 06:56, 25 April 2008 (UTC)
PeR, you are just pretending that you don't understand. If it doesn't co-rotate, there is no centrifugal force. The object sits still unaffected.
If it fully co-rotates, the radial centrifugal force is given by v^2/r, where v is the tangential speed.
If it partially co-rotates, the centrifugal force is given by the same equation but with the speed changed to the tangential speed of the object in question, with respect to the same rotation axis.
At the moment, you are just in denial of reality. For too long, you have had your mind focused on some irrelevant fictitious form of centrifugal force and there is a group of you closing ranks to defend that erroneous way of thinking.
- I'm sorry, but you don't understand. This article is completely about that 'erroneous' way of thinking as you put it. The problem you have is a) it's self consistent b) it models reality correctly (it must do, since it's derived from an inertial frame using correct logic).- (User) WolfKeeper (Talk) 17:22, 25 April 2008 (UTC)
So far, there is you, Henning Makholm, RRacecarr, Wolfkeeper, and now FiziksFighter. I am expecting more to arrive to back you all up before this is over.
I have no doubt that you will all attempt to confound the issue with a hail of bogus mathematics. But this issue doesn't depend on maths. It depends on basic common sense.
Only a fool thinks that the background stars are being subjected to a combination of fictitious forces that result in a final inward fictitious radial centripetal force. David Tombe (talk) 16:22, 25 April 2008 (UTC)
- The thing is, maths is a model of reality, not reality. In the rotating non inertial frame model that is the subject of the article, yes, yes they are. You're just going to have to live with that.- (User) WolfKeeper (Talk) 17:22, 25 April 2008 (UTC)
Article should be split
The two sorts of centrifugal force are distinct topics. Distinct topics should have their own articles- that's one of the differences between a dictionary and an encyclopedia. Just because they are called the same doesn't meant they get to go in the same article. In fact, it's wrong to have them in the same article in the wikipedia.- (User) WolfKeeper (Talk) 05:42, 25 April 2008 (UTC)
- Agreed. I think there should be an article entitled Fictitious forces in a rotating reference frame, that would be a subarticle of both this one, Fictitious force, and Coriolis force. It is much easier to discuss centrifugal and Coriolis forces together than one at a time, since you rarely have one without the other. A significant portion of the current article is devoted to explaining the difference between the two meanings of the term. Perhaps it should be moved to Centrifugal force (disambiguation). Then we create a new article entitled Centrifugal force (reaction force), and leave Centrifugal force as a redirect to the disambig. For good measure we should also create a page Centrifugal force (fictitious) that redirects to Fictitious forces in a rotating reference frame. --PeR (talk) 06:47, 25 April 2008 (UTC)
- Or maybe we could move this article to centrifugal force (fictitious) with a redirect from centrifugal force and split off the real force to centrifugal force (reaction force) and put a cross-reference 'for' at the top. I'm leaning against a disamb at this time, there's only two meanings and I'm pretty sure that the real force isn't being referenced very much.- (User) WolfKeeper (Talk) 17:55, 25 April 2008 (UTC)
- Or possibly instead of centrifugal force (fictitious) we could move it to centrifugal effect which would talk about the acceleration, and then include the force equation as well. There just doesn't seem to be quite the same degree of garbage going on over at coriolis effect and there's more symmetry in the wiki better reflecting the physics.- (User) WolfKeeper (Talk) 18:03, 25 April 2008 (UTC)
- I like Wolf 1 a lot. Not so big on Wolf 2 (centrifugal effect). It is not in such common usage as Coriolis effect, and the same discussion of acceleration can be included at both the centrifugal force articles.Rracecarr (talk) 18:13, 25 April 2008 (UTC)
- Yes, I agree. I did a google on 'centrifugal effect' and it's not common enough to be an article title.- (User) WolfKeeper (Talk) 19:13, 25 April 2008 (UTC)
- I also thought that the classical use of the term was uncommon these days, but I'm starting to change my mind. It seems to be used applied mechanics. And I have heard materials science people use the term correctly in the classical sense when discussing rotating parts in machinery. I think, because the term is not introduced at high-school level, people from different fields will have learned the term with different meanings, and people who learned about the fictitious kind from a theoretical physics class might never realize that people who studied statics use the same term with a different meaning. --PeR (talk) 21:50, 25 April 2008 (UTC)
- Sure, if it wasn't in use, we wouldn't have it in an article. It's in the article because we found references to it, less than to the d'Alembert force version, but it's definitely in use.- (User) WolfKeeper (Talk) 22:08, 25 April 2008 (UTC)
OK, I've created Reactive centrifugal force, on reflection it seemed a better name than Centrifugal force (reactive), but we can always move it, or add redirects if necessary.- (User) WolfKeeper (Talk) 02:37, 27 April 2008 (UTC)
- Good, I think. That leaves us with the question of where to explain the differences between the two meanings. They are confused often enough (and the confusion can be difficult enough to dispel) that I think it falls within our encyclopedic mandate to set the difference straight explicitly. –Henning Makholm 02:55, 27 April 2008 (UTC)
- Ok, I've hacked the article a bit, I'm not totally happy with it, but it's about 60% there. I think we need to prune back the reactive force more, and probably explain more about the reactive force in its own article.- (User) WolfKeeper (Talk) 03:02, 27 April 2008 (UTC)
- Agreed, though I think we may have more than 40% to go yet. The previous consensus state of the article was not quite a model of brilliance and clarity in its explanation of the fictitious force, and we should be able to do better if we don't have to do it in the context of an (apparent!) controversy between two meanings of the word. In particular, I think the "Rotating reference frames" and "Fictitious forces" sections overlap each other without good reason; they should be combined into a single section which tells it all in a logical sequence.
- As for references to the reactive force, I think there should be the hatnote, plus a more verbose discussion late in the article, probably including the table of differences. I suggest that the "confusion and misconception" section might be coopted for this, and possibly be given a more encyclopedic-sounding title along the way. –Henning Makholm 03:15, 27 April 2008 (UTC)
Article should be split into three ?
It would seem now that the article should be split into three.
(a) The ultra fictitious centrifugal force associated with the mathematical games surrounding the articial circle produced by a rotating frame of refeence.
(b) The 'inertial' centrifugal force which invokes Archimedes' principle in a centrifuge and causes real differential effects on the particles in a solution observable from all frames of reference.
(c) The knock on effect that a body being acted upon by (2) has on any object obstructing its path.David Tombe (talk) 07:11, 25 April 2008 (UTC)
- No. --PeR (talk) 07:48, 25 April 2008 (UTC)
Well PeR, since you have been so disagreeable up until now, I would hardly have expected any other response from you.
I will however take this matter to the wiki physics project.
The question will be put. Are these two effects the same thing?
(a) An object in the rest frame that is not co-rotating with a rotating frame appears to trace out a circle in the rotating frame. An example of this is the stars as they cross the sky at night time.
(b) When objects co-rotate with a rotating frame, a radial centrifugal force is induced which is real enough to invoke Archimedes' principle. An example is the centrifuge.
Are these two effects the same?David Tombe (talk) 08:50, 25 April 2008 (UTC)
- Just make sure you include a link to this page, so that people can catch up on what has already been said. --PeR (talk) 09:24, 25 April 2008 (UTC)
Electrodynamicists edit's
Electrodynamicist, while I appreciate you reverting to that concise introduction, my own belief now is that we should be dealing with the so-called consensus version on one point at a time.
The issue ultimately comes down to the fact that some of the editors here want to focus attention exclusively on the ultra fictitious centrifugal force which they create around stationary particles just by palying around with maths, and wrongly two.David Tombe (talk) 14:48, 25 April 2008 (UTC)
New tack
Maybe we can write the article in such a way that everyone is happy. As I understand it, David Tombe is unhappy that the consensus version does not discuss in the intro, in a straightforward, plain English way, things like buckets swinging over heads. I think he may be right that such a "common sense" description is in order. However, the rest of us are not happy with phrases like outward radial force which acts on objects moving in a circular path, since such a force does not actually exist. Surely there is a wording that will satisfy everyone.
Working in that direction, I have a couple of questions for David Tombe:
1) When an elevator starts to move upward, you feel heavier. What do you call that "force"?
2) Do you acknowledge that what you call "ultra mathematical games" are, fundamentally, exactly the same centrifugal force you want the article to focus on, just expressed in a different language? Would you agree to an article that talked about water in a bucket and moved smoothly on to discuss that situation from the reference frame of the bucket, and so to fictitious forces? Rracecarr (talk) 17:52, 25 April 2008 (UTC)
- Rracecarr, regarding the man being accelerated upwards in an elevator, I don't have a special name for that force. The force acts against gravity and there is a resultant upward force. It's the same as any contact force. It causes acceleration.
- On the maths, I am well versed in the equations for a rotating frame of reference. But I believe that these equations can be used to cloud the underlying realities of the situation.
- When a man is stationary in an inertial frame, then there is nothing happening. It is irrelevant that somebody in a rotating frame views him as travelling in a circle.
- But when a centrifuge causes particles to move outwards to the edge, we have a very real effect that has caused relative motion between different particles in the solution. We have invoked Archimedes' principle.
- One should be able to see that these two situations are not the same, without having to go into any maths.
- At least I know now that it is because of the maths that you think that the situations are the same.
- Regarding that maths, one key point is that Wolfkeeper seems to think that the cross product expression for Coriolis force proves that the Coriolis force acts in any direction. He is overlooking the fact that the cross product was introduced to be in the tangential direction with the magnitude being the product of the angular speed and a radially aligned magnitude.
- Another point is that in order for circular motion to occur, we need to have a net zero radial force. In the circular artifact scenario, the forces aren't balanced
- And a third point is that when you study the derivation of those equations, you will see that the angular velocity is intricately linked to the linear velocity. There has to be a physical connection between the v term and the ω term. In your artificial circle example, the stationary object has got no physical connection with the motion.
- So nothing happens. It is neither centrifugal force nor Coriolis force. It is merely a circular motion artifact.
- But we shouldn't need to go into this maths to have to see that. It should be obvious from a common sense premises that centrifugal force only occurs on an object which is being constrained to move in a curved path.
- On your second question, I would adopt the policy that all articles should began with a simple and basic introduction but maybe brightened up with one or two obscure points of interest.
- As the article progresses, I would never object to more and more complicated and specialized aspects being introduced. The issue of rotating frames of reference could be introduced as a specialized section.
- The current introduction could be re-worded by giving a basic description of centrifugal force as per the kind that is experienced in everyday situations. A clarification clause should be introduced to make sure that readers don't confuse it with centripetal force.
- The swerving car example could then be given. Or indeed the artificially induced gravity scenario of a rotating cylinder. But I don't believe that the knock on effect needs to be emphasized as a separate centrifugal force. It is merely what weight is to gravity.
- Finally, Wolfkeeper asked why is there never a similar dispute going on at the Coriolis force page? The reason is that the discussion surrounding where Coriolis force is real and where it is fictitious, and where it doesn't exist at all is to too complicated, too controversial and too likely to break wikipedia's rules agains original research and opinion. Furthermore, even at best, the man in the street is not familiar with what Coriolis force really means, and there is no easy way to explain it without involving alot of arguments. So its best to leave that article for the time being.
- Centrifugal force has a clean cut off between what is actually centrifugal force and what has been confused for centrifugal force. That is because it is a radial effect. But Coriolis force is a tangential effect and so circular motion can create an artifact which gets confused with what genuinely is a fictitious Coriolis force. Then there is the controversy surrounding where Coriolis force becomes real. So we have three stages of analysis in Coriolis force. the Foucault pendulum at the poles is only an artifact. The missile flying through the air from Miami to New York is Coriolis force but purely fictitious. Finally the atmosphere involves a v that is physically connected with an entrained ω and so the effects can be real and viewable from outer space. The latter scenario corresponds by analogy to the reality of the centrifuge where the v and the ω are physically connected. David Tombe (talk) 19:05, 25 April 2008 (UTC)
- All I know is, coriolis and centrifugal force fall out of a completely valid mathematical manipulation of a general equation of motion with respect to an inertial reference frame, and in that sense at least, they are very, very real.- (User) WolfKeeper (Talk) 19:30, 25 April 2008 (UTC)
- Let's stick with the elevator for a minute. The force experienced by the person in the elevator is fundamentally the same as the centrifugal force experience by particles in a centrifuge, right? Both are the result of acceleration--the only difference is that in the elevator it is linear acceleration, whereas in the centrifuge it is centripetal acceleration. Agree? Rracecarr (talk) 20:20, 25 April 2008 (UTC)
Bucket swinging over head
I agree with David Tombe, that the introduction needs to be more accessible, and that swinging a bucket over one's head is a good example. Here's a draft text:
- The term "Centrifugal force" has two different meanings. The classical meaning of the term, as used by Isaac Newton and others, is to denote the reaction force to a centripetal force. In modern usage the term can also be used to denote a fictitious force that occurs in a rotating reference frame.
- An example of the classical use of the term is the statement.
- When swinging a bucket over your head, the bucket pulls on your hand with a centrifugal force.
- The hand exerts a centripetal force (action) on the bucket, and the bucket in turn exerts a centrifugal force (reaction) on the hand.
- In contrast, an example of the modern usage would be:
- When swinging a bucket of water over your head, the water stays in place due to the centrifugal force.
- This sentence considers a reference frame that rotates with the bucket. (In an inertial reference the water could not be said to "stay in place", since it is moving in a circle along with the bucket.) The force referred to here is a fictitious, or pseudo force that is not caused by physical interaction, and therefore has no corresponding reaction force in the rotating frame. It is simply a mathematical construction that makes a it possible to describe the system as seen from the bucket's perspective.
I'll work it into the introduction once the edit war there has ceased.
--PeR (talk) 21:28, 25 April 2008 (UTC)
This looks good, PeR. How about removing the hand from the example:
- The term "Centrifugal force" has two different meanings. The classical meaning of the term, as used by Isaac Newton and others, is to denote the reaction force to a centripetal force. In modern usage the term can also be used to denote a fictitious force that occurs in a rotating reference frame.
- An example of the classical use of the term is the statement.
- When swinging a bucket of water over your head, the water pushes on the bucket with a centrifugal force.
- The bucket exerts a centripetal force (action) on the water, and the water in turn exerts a centrifugal force (reaction) on the bucket.
- In contrast, an example of the modern usage would be:
- When swinging a bucket of water over your head, the centrifugal force acting on the water causes it to stay in place.
- This sentence considers a reference frame that rotates with the bucket. (In an inertial reference the water could not be said to "stay in place", since it is moving in a circle along with the bucket.) The force referred to here is a fictitious, or pseudo force that is not caused by physical interaction, and therefore has no corresponding reaction force in the rotating frame. It is simply a mathematical construction that makes a it possible to describe the system as seen from the bucket's perspective.
Rracecarr (talk) 21:44, 25 April 2008 (UTC)
- Better with the removed hand, but I like my version better for the second quote. (Shorter, less complex). --PeR (talk) 22:10, 25 April 2008 (UTC)
- I thought it was important to emphasize a difference between the two quotes: in the first the force acts on the bucket, in the second, it acts on the water. Rracecarr (talk) 22:22, 25 April 2008 (UTC)
- Yep. On second thought, I like your version better for both quotes. --PeR (talk) 22:24, 25 April 2008 (UTC)
You guys need to actually read Newton's book since what you say here is wrong. From reading what is written here, I see what you dont know what you are doing and dont understand the arguments involved at all. Obviously this means the article does need major changes to correct the misconceptions of the editors who wrote the so called consensus version. I also suggest you actually educate yourselves before writing any more articles for wikipedia.72.64.46.3 (talk) 23:13, 25 April 2008 (UTC)
- Maybe it is you, David Tombe, who needs education. That would seem the more likely possibility, since you are the only one who thinks the above is wrong. Rracecarr (talk) 02:57, 26 April 2008 (UTC)
Rracecarr, I think we need to be quite clear about this. I am not the anonymous writing from 72.64.46.3 David Tombe (talk) 07:16, 26 April 2008 (UTC)
Silly of me. Why would I assume that about 4 anon IPs, all in the Hampton, VA, USA area, doing your reverting for you and answering questions aimed at you, none of which has ever contributed to any other articles? Rracecarr (talk) 16:04, 26 April 2008 (UTC)
- Actually, I think the rude anon in Hampton, VA, might be someone else. (Possibly a friend of David's.) The recent edits by User:58.10.103.101, is from a different country, and David has signed contributions from that country in his own name before. --PeR (talk) 16:24, 26 April 2008 (UTC)
- Yes, I knew 58.10.103.101 was David, but that does not mean the VA anon isn't. Still, I have struck the sarcastic comment, and I will keep my other suspicions to myself. Rracecarr (talk) 16:31, 26 April 2008 (UTC)
Replies to RRacecarr, PeR, and Wolfkeeper
Rracecarr, the upward force that the elevator floor is applying to the person inside the elevator is definitely not the same kind of force as the centrifugal force which causes the heavier particles to move outwards in a centrifuge.
- It is exactly, precisely the same kind of force. In the elevator, the acceleration producing the "force" is linear. In a centrifuge, it is centripetal. That is the only difference. If you had an elevator that would continue to accelerate hard for a long while, it would work just as well as a centrifuge for separating particles, and for just the same reason. If you can understand that, I think a lot of the problems we're having will go away. Rracecarr (talk) 16:20, 26 April 2008 (UTC)
I looked at your new edits. I noticed that you emphasized the fact that the inward centripetal force is being caused by an object. That immediately tells me that you are leading towards a point, with that point being almost certainly related to the issue of action and reaction.
I think that one of the big mistakes that people are making here is in actually trying to decide which force is the action and which force is the reaction. We don't need to bother doing that. When an object moves in a circle, the outward centrifugal force and the inward centripetal force will always be balanced.
- I actually agree with you here. There is technically no way of defining which is the action and which the reaction. The thing that is important to remember is that the centripetal force acts on the object moving in a circle, but the centrifugal force does not. It acts on the thing exerts the centripetal force on the object moving in a circle. Rracecarr (talk) 16:20, 26 April 2008 (UTC)
You must also remember that the centripetal force does not have to be caused by an object. It could be caused by gravity, electrostatics, or indeed the Lorentz force.
- On a macroscopic scale, it is ALWAYS caused by the forces you mention--gravitational or electromagnetic. The other kinds of force only act over microscopic distances. But gravitational and electromagnetic fields do not occur in isolation. They are the result of masses and charges. So yes, the centripetal force is always exerted by an object, and that object is always subject to a reactive centrifugal force. Rracecarr (talk) 16:20, 26 April 2008 (UTC)
Therefore, always remember to make your point in the most general way.
The most general way of describing a centrifugal force is that it is an outward force which occurs when any object is constrained to move in a curved path.
- On what does this force act? You need to be clear. Rracecarr (talk) 16:20, 26 April 2008 (UTC)
I hope that you can now understand why we don't need to differentiate between a centrifugal force and a reactive centrifugal force, especially in the introduction. I tried to make that simple statement, I then added the fact that we shouldn't confuse it with centripetal force, and I finally stated that whereas in former times, centrifugal force was considered to be real, the modern day view is that it is fictitious.David Tombe (talk) 06:52, 26 April 2008 (UTC)
- Wolfkeeper, I know exactly the derivation that you are talking about. I am very familiar with it. But never lose track of the physical reality to which it applies. There are two key aspects of this maths which you are overlooking,
- (1) The Coriolis term is specifically derived to be in the tangential direction. It is a tangential effect arising from a radial motion, whereas the centrifugal force is a radial effect arising from a tangential motion.
- (2) The maths only has physical meaning when v and ω are physically connected. For centrifugal force this means co-rotation. For Coriolis force, this means that v has a physical connection with the source of the rotation, such as is the case with the hydrodynamics of cyclones, or with a Foucault pendulum at mid-latitudes.
- In the case of there being no physical connection, such as with a missile or a bird flying over a children's roundabaout, then there will be a fictitious Coriolis force, but only acting on radial motion. The artificial effect which acts on tangential motion in the unconnected state is not even Coriolis force.
- It's all very well coming up with this maths, and the maths is indeed correct. But never lose sight of the physical meaning of the maths. David Tombe (talk) 07:03, 26 April 2008 (UTC)
PeR, Unlike with Coriolis force, centrifugal force is something that the public are more aware of. The swerving car will almost certainly be the first situatation in which a child will become subconsciously aware of it, whereas the bucket of water being swung over the head will be the first situation that will draw attention to it. The centrifuge as an engineering tool will follow on at high.
So either the bucket of water or the swerving car make good examples in the introduction. But we must first state the general description of the centrifugal force.
Take note of what I said above to Wolfkeeper. Neither centrifugal force nor Coriolis force are the artificial tangential effects which are viewed from a rotating frame of reference. You clouded your point up when you started introducing this dimension.
You began good and gave an example of centrifugal force showing that the water in the bucket was defying gravity. Then you contradicted yourself by trying to argue that in the rotating frame there was no such force. Of course there is. David Tombe (talk) 07:14, 26 April 2008 (UTC)
- PeR, I just looked at your last paragraph again. You are very badly confused. You are equating the water in the swinging bucket with the ultra fictitious artificial circle produced when a stationary object is viewed from a rotating frame of reference. The latter inolves no forces at all. In the water in the bucket, centrifugal force causes pressure.
- People can be hurt by centrifugal force, but nobody has ever been hurt as a direct result of being viewed from a rotating frame of reference.David Tombe (talk) 07:23, 26 April 2008 (UTC)
Reply to FyzixFighter
FyzixFighter, You have endorsed Rracecarr's latest edits. Let's look at it,
"A mass undergoing circular motion constantly accelerates toward the center of the circle. This centripetal acceleration is caused by a centripetal force, which is applied to the mass by some other object. In accordance with Newton's Third Law of Motion, the mass exerts an equal and opposite force on the object. This is the real or "reactive" centrifugal force: it is directed away from the center of rotation, and is exerted by the rotating mass on the object which imposes the centripetal acceleration. Although this sense was used by Isaac Newton, it is only occasionally used in modern discussions."
Would you agree that centripetal force can by cuased other than by contact action from an object? For example gravity, electrostatics, or the Lorentz force.
Would you agree that this passage could be simply stated as,
"When an object moves in circular motion, the centripetal force and the centrifugal force are balanced" ?
Why not actually think about the issues before joining up with a team for an edit war? Let's see you here in the debate. David Tombe (talk) 07:37, 26 April 2008 (UTC)
- I just woke up and wow... I don't want to derail the already existing conversation so I'll just answer up here. No, I would not say that the centripetal force and centrifugal force are balanced because in order for two forces to "balance", they must be acting on the same object. The two forces in this case are not acting on the same object so saying they are balanced makes no sense. They are equal and opposite, but that does not mean they are balanced. We do not say that the force of the earth on the apple is balanced by the force of the apple on the earth as the earth falls. Now frankly, it's not up to us to explain classical mechanics to you. You cry foul when we don't have a reference, yet you have never provided a reliable source that says there are three types of "centrifugal force" - you invoke common sense, but in my experience common sense is not a reliable source. By the way, here's a few references for the two types of centrifugal force - "A Dictionary of Physics", pg 57, Oxford ; New York : Oxford University Press, 1996 and "McGraw-Hill Dictionary of Physics", pg 77, New York : McGraw-Hill, 1984. --FyzixFighter (talk) 16:29, 26 April 2008 (UTC)
- You say that an object moves in a circle when forces are balanced. I think I read somewhere that it would move in a straight line. Is that a statement you found in a book, or one that you made up yourself? --PeR (talk) 07:39, 26 April 2008 (UTC)
No PeR. I said that when something moves in a circle, the radial forces are balanced. You completely twisted what I said because you are now realizing that you have been totally wrong all along. David Tombe (talk) 07:42, 26 April 2008 (UTC)
- No, I honestly don't understand what you mean. In your mind, what forces are acting upon the object that moves in a circle? Could you list them all, and say what they sum up to? --PeR (talk) 07:52, 26 April 2008 (UTC)
PeR, when an object is moving in a circle, there is a centripetal force acting inwards radially and a centrifugal force acting outwards radially. The inward centripetal force could be supplied by anything from tension in a string, to pressure from the floor of a rotating cylinder, or to gravity, electrostatics, or the Lorentz force.
At any rate, if the motion is circular, the centrifugal force exactly cancels with the centripetal force because there is zero radial acceleration.
If however the two forces are not balanced, the resulting motion will be more complicated. The most well known case is in planetary orbits. In a Keplerian ellipse, parabola or hyperbola, the outward centrifugal force does not balance with the inward gravitational force. David Tombe (talk) 09:45, 26 April 2008 (UTC)
- (Let's just talk about circular motion for the time being.) You say there is "zero radial acceleration". Do you mean that the circular motion is due to acceleration in some other direction? (If so: Which direction? What causes that acceleration?) Or are you saying that an object can deviate from a straight line without acceleration? --PeR (talk) 10:45, 26 April 2008 (UTC)
PeR, We have not addressed the issue of how the object came to be moving in circular motion. We are merely focusing on the fact that when an object is already moving in circular motion that there can be no net radial acceleration, otherwise it wouldn't be circular motion. Hence the centrifugal force and the centripetal forces will be balanced.
You will never understand this issue if you continue to focus your attention on the special case of circular motion. I suggest that you study the general case of motion that results when an inward radial gravity force acts in tandem with an outward radial centrifugal force.
There are many possible results in terms of size, direction etc. all dependent on the initial conditions. But all solutions will come down to either an ellipse, a parabola, or a hyperbola, The circle is just a special case.
And so yes, it is possible to have an obect moving in a curved path with no net acceleration if that curved path forms part of a circle. David Tombe (talk) 11:20, 26 April 2008 (UTC)
- You say:
- ...it is possible to have an obect moving in a curved path with no net acceleration if that curved path forms part of a circle.
- Now, most textbooks define acceleration as "rate of change in velocity". Do you use a different definition? Or do you propose that an object moving in a circle never changes its velocity? --PeR (talk) 12:06, 26 April 2008 (UTC)
- Again I say you need to learn some physics. The velocity does not change only the direction changes. Your understanding is limited. You need to recuse yourself from editing, along with the rest of the fools here, because you obviously dont know physics.71.251.185.86 (talk) 13:29, 26 April 2008 (UTC)
PeR, A centripetal force alone cannot cause a circular motion. It can do so only in conjunction with a centrifugal force. The two of them act together in tandem and maintain the object in the tangential direction while maintaining the tangential speed. The net radial acceleration is zero.
Consider a weight being swung around in a circle on the end of the string. The tension which supplies the inward centripetal force only comes into existence as a reaction to the outward centrifugal force.
That is in total contrast to all the assertions that had been made on the main page falsely saying that centrifugal force is a reaction to a centripetal force. In the case of the weight on the end of the string, it is the other way around. David Tombe (talk) 13:50, 26 April 2008 (UTC)
- David, I'd really like to hear your answer to my question above. Feel free to answer here, or on your talk page. --PeR (talk) 14:41, 26 April 2008 (UTC)
PeR, I go along with the official definition of acceleration. Now using the very same maths that you use to promote your theories about the rotating frame of reference, we consider a position vector in the radial direction. Differentiate it. It is a product because it involves the unit vector which has to be dealt with separately to account for direction change.
The final result is an expression for acceleration in the radial direction and acceleration in the tangential direction. The tangential direction contains the Coriolis force but we are not interested in that right now.
When the centrifugal force, which is always radially outwards, is balanced by another inward radial force, then we will have zero radial acceleration and hence circular motion.
If there is no tangential acceleration and hence no angular acceleration, then we will have a net zero acceleration for an object moving in a circle.David Tombe (talk) 14:49, 26 April 2008 (UTC)
- You say we have zero net acceleration, so by the textbook definition, zero change in velocity. Velocity includes direction of movement, so you are saying that an object can move in a circle without changing its direction of movement? Or do you use a different definition of velocity? --PeR (talk) 15:28, 26 April 2008 (UTC)
- Look at the old talk archive -- it appears that David still insists on taking unadjusted coordinate accelerations in a polar coordinate system. That's how he thinks uniform circular movement has no net acceleration. –Henning Makholm 01:08, 27 April 2008 (UTC)
- If I can also jump in, David take that same analysis that you just put above to looking at what kind of acceleration is required for circular motion. But let's not start out at the position vector, let's go right to the velocity vector. The velocity vector in constant circular motion is v*theta_hat, where v is a constant. Differentiating this with respect to time gives 0*omega_hat+v*d(omega_hat)/dt. Now when you go through the math for the unit vectors, you will find that d(omega_hat)/dt is -d(omega)/dt*r_hat (honestly this is a lot easier to see when done in cartesian unit vectors, and will yield the same results - most calculus-based, freshman physics textbooks go this route). So even though the motion is circular, the acceleration is radial. I'm guessing though that you're going to disagree with me on the d(omega_hat)/dt = -d(omega)/dt*r_hat bit. --FyzixFighter (talk) 16:52, 26 April 2008 (UTC)
Reply to PeR and FyzixFighter
You wish to look at the picture from an inertial Cartesian reference frame thinking that the centrifugal force will disappear.
In an inertial Cartesian reference frame, a particle in circular motion will indeed have an acceleration. The direction of the particle's velocity is constantly changing. It will have an acceleration always pointing in towards the centre of the circle.
That inward acceleration will be in the radial direction in relation to the circle itself. The outward centrifugal force will still be there too in the radial direction. It doesn't go away. Both of these forces exist in the radial direction.
The reality of the centrifugal force as an absolute fact can be proved because the effects of a centrifuge are observed by both somebody riding on the centrifuge and by a person sitting in the corner of the room.
From the tangential/radial perspective, there is no acceleration. The centripetal and centrifugal forces exactly cancel.
From the inertial Cartesian perspective, these same two forces work in tandem to cause the acceleration that changes the direction of the particle, but not its speed.
There is no question of having the centripetal force acting alone. In some cases, such as the weight being spun on the end of a string, the centripetal force is only activated by the centrifugal force.
If the string were to be replaced by a spring, we could have an elliptical motion in which the two forces alternate their magnitudes.
You cannot make the very real centrifugal force vanish simply by viewing the picture from the laboratory frame. David Tombe (talk) 05:37, 27 April 2008 (UTC)
Reply to Rracecarr
Rracecarr, regarding the elevator, the correct analogy that you are looking for is,
(i) Centrifugal force is to gravity,
whereas,
(ii) Centripetal force is to 'Normal Reaction'.
You will have to learn to generalize your approach and not confine the study to circular motion, and contact forces in which the centrifugal force is causing a pressure. David Tombe (talk) 05:43, 27 April 2008 (UTC)
General Comments on Splitting the Article
This split has been motivated as a knee-jerk reaction to save face on realizing that the so called consensus version contained many errors. It has effectively moved the one and only centrifugal force off to a new page.
The remaining page deals with a pure artifact that arises from a misinterpretaion of mathematics, and it describes neither centrifugal force nor Coriolis force.
The real centrifugal force has now been labelled as 'Reactive centrifugal force' in a separate article, when in fact there are many scenarios when it is clearly not a reaction.
Take planetary orbital theory as an example. The centrifugal force is not acting as a reaction to gravity. It acts in tandem with gravity to yield elliptical orbits.
An object being swung around on the end of a string induces the tension in the string to provide the centripetal force. Clearly in this scenario, the centrifugal force is the pro-active force.
The situation is now a worse mess than ever.David Tombe (talk) 06:10, 27 April 2008 (UTC)
Reductio ad absurdum
David, in our previous discussion, you started with the hypothesis
- When an object moves in circular motion, the centripetal force and the centrifugal force are balanced
and that lead you to the conclusion
- ...it is possible to have an object moving in a curved path with no net acceleration if that curved path forms part of a circle.
Now you are saying
- In an inertial Cartesian reference frame, a particle in circular motion will indeed have an acceleration. The direction of the particle's velocity is constantly changing. It will have an acceleration always pointing in towards the centre of the circle
which means that your previous conclusion was false. My question to you is then: Was your initial hypothesis also false? Or was there an error in one of the steps from the hypothesis to the conclusion? In that case: Which step?
--PeR (talk) 06:34, 27 April 2008 (UTC)
PeR, using radial and tangential coordinates, there is no net acceleration in circular motion. Using Cartesian coordinates there is.
But the underlying reality that you are denying is that in either case, the motion in question is the result of a centripetal force acting in tandem with a centrifugal force.
You are desperately trying to make centrifugal force go away. Your colleagues have now even moved it to a separate page.
You need to study planetary orbital theory. Two forces combine together to yield an ellipse, a parabola, or a hyperbola. The circle is a special case of the ellipse. You cannot make the centrifugal force go away by focusing attention on circular motion in a Cartesian reference frame. David Tombe (talk) 08:07, 27 April 2008 (UTC)
- You didn't answer my question. --PeR (talk) 08:16, 27 April 2008 (UTC)
PeR, your question was based on the supposition that my previous assertion had been false. My previous assertion that it is possible to have circular motion with no acceleration is a correct assertion. It occurs when we view circular motion in terms of radial and tangential coordinates.
Changing to different coordinate systems can change accelerations. But it can never change the reality of absolute effects such as Archimedes' principle occuring in a centrifuge. David Tombe (talk) 08:47, 27 April 2008 (UTC)
- I'm still not sure what you mean. Are you saying that your previous statement
- the centripetal force and the centrifugal force are balanced
- only is true when viewed in "radial and tangential coordinates", but not in stationary Cartesian coordinates?
- --PeR (talk) 09:00, 27 April 2008 (UTC)
PeR, in Cartesian coordinates, in the special case of circular motion, the combined effect of the centrifugal force and the centripetal force is to cause that circular motion. The combination changes the direction of the object without effecting its radial speed. It's up to you whether or not you want to call that 'balanced'. But at the end of the day, it has got no bearing on the main issue. Centrifugal force has to be present in circular motion. You are trying to argue to the contrary. You are trying to tell me that we can have circular motion with a centripetal force alone.
Consider the special case of a circular gravity orbit as viewed from a Cartesian frame. If the centrifugal force ceased, then the gravity force that had been acting as the centripetal force would bring the object straight to the center. A circular motion cannot contain only a centripetal force. It has to have both a centripetal force and a centrifugal force. David Tombe (talk) 09:16, 27 April 2008 (UTC)
- According to the article on force, there are only 4 types of fundamental forces. In the example you just provided, the centripetal force is gravitational. Which type is the centrifugal force?Rracecarr (talk) 15:42, 27 April 2008 (UTC)
- By "balanced" it thought you meant "the sum of the centrifugal force and the centripetal force is zero". If that is not what you meant, then please clarify. What, according to you, is the sum of the forces acting on an object that moves in a circle in a stationary Cartesian coordinate system? --PeR (talk) 09:27, 27 April 2008 (UTC)
- PeR, for the purposes of this discussion, the only thing that matters is that the two forces are balanced in radial and tangential coordinates. Your entire argument about the artificial circle is explained in radial and tangential coordinates, and in that case, the two forces are definitely not balanced.
- We are not going to cloud the issue by discussing it all in Cartesian coordinates. Have you ever seen the expression for centripetal force written in Cartesian coordinates? —Preceding unsigned comment added by David Tombe (talk • contribs) 07:42, 28 April 2008 (UTC)
Reply to Racecarr regarding the centrifuge
Rracecarr, in the centrifuge, heavier particles actually move past lighter particles. This is a real effect which is observed from every frame of reference. For this effect to occur, a force must be acting and it cannot be centripetal force because the particles have not yet contacted the reaction surface, notwithstanding the fact that centripetal force is in the wrong direction anyway.
The fictitious circle that you are emphasizing is not the same situation at all. It is merely an artifact.
The maths which you believe unites the two situations is only applicable when the v and the ω are physically connected. That follows from the derivation. And if you study the derivation, you will see that when the velocity formula is expanded into the acceleration formula, the v in the v times ω term gets replaced with another v which is only radial.
In other words, that maths does not apply to the artificial circle. You have unanchored the maths from the physical reality to which it applies. David Tombe (talk) 06:20, 28 April 2008 (UTC)
Comments on the Split
What appears to have happened now is that the ultra fictitious case of centrifugal force, which is based on a faulty interpretation of maths, has been moved to a position of primacy in an article all of its own, as being the flagship carrier for centrifugal force. It seems that the editors think that this is what the public are looking for when they go to look up centrifugal force.
Centrifugal force is no loner the real effect that occurs in the centrifuge. It is now a fictitious circular motion that we observe from a rotating frame of reference.
Well as far as that is current textbook theory, then the introduction is basically correct now since I have removed the bit about the object having to be moving. If we're going to have a wrong article, better that it is correctly wrong.
Unfortunately though, real centrifugal force has been moved away to a page of its own where people are less likely to look. And it has been totally confused by giving it the misnomer 'Reactive centrifugal Force'. Yet we can see clearly in the case of a weight being swung around on the end of the string that centrifugal force is anything but reactive. And more so in the centrifuge where the heavier particles push their way through the lighter particles to make their way to the outer edge. What is that supposed to be in reaction to? Certainly not the centripetal force as is claimed in the article.
Then to make matters worse, the article gives the impression that centrifugal force is only something that occurs with circular motion, and not elliptical or hyperbolic motion. It would seem that the latter two concepts were too advanced for whoever wrote the article.
And finally, whoever wrote the article considers contact pressure with an object to be the only legitimate means of bringing about centrifugal force. Gravity, electrostatics, and the Lorentz force have been excluded.
All attempts to generalize it to curved motion caused by any force have been fiercely resisted particularly by PeR and FyzixFighter.
Clearly there is team vandalism going on at present on this article. It is now in a worse state than when the edit war began. David Tombe (talk) 07:57, 28 April 2008 (UTC)
Reply to PeR
PeR, there is no need to leave formal warnings for me in my tray. You have accused me of wikistalking. That is very rich coming from you. It's a case of the pot calling the kettle black.
You and FyzixFighter have been actively making a point of deleteing every single edit that I make. I am trying to improve this article. I tried to generalize the definition of centrifugal force but both of you reverted it to a high school version that shies away from anything more complicated than a circle.
That is wikistalking if ever there was a case. You are simply making that statement that you will let Wolfkeeper and Rracecarr edit these pages but under no account are you going to alow me to have the slightest input. That is wikistalking.
So do you want to call a truce, or do you want the administration to be brought in? David Tombe (talk) 08:04, 28 April 2008 (UTC)
Categories:
 . As you can see, since it is a cross-product, if v is perpendicular to r then it acts completely radially.- (
. As you can see, since it is a cross-product, if v is perpendicular to r then it acts completely radially.- (