| Revision as of 17:38, 26 January 2007 editJulesH (talk | contribs)Extended confirmed users5,584 edits →Other usages: Not relevant to this page← Previous edit | Latest revision as of 01:40, 17 October 2023 edit undoInternetArchiveBot (talk | contribs)Bots, Pending changes reviewers5,388,208 edits Rescuing 1 sources and tagging 0 as dead.) #IABot (v2.0.9.5) (Whoop whoop pull up - 15814 | ||
| (28 intermediate revisions by 25 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Block cipher}} | |||
| {{More footnotes|date=September 2015}} | |||
| {{Infobox block cipher | {{Infobox block cipher | ||
| | name = FEAL | | name = FEAL | ||
| Line 4: | Line 6: | ||
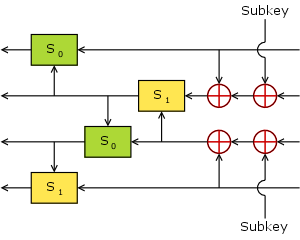
| | caption = The FEAL Feistel function | | caption = The FEAL Feistel function | ||
| | designers = Akihiro Shimizu and Shoji Miyaguchi (NTT) | | designers = Akihiro Shimizu and Shoji Miyaguchi (NTT) | ||
| | publish date = FEAL-4 in |
| publish date = FEAL-4 in 1987; FEAL-N/NX in 1990 | ||
| | derived from = | | derived from = | ||
| | derived to = | | derived to = | ||
| Line 14: | Line 16: | ||
| }} | }} | ||
| In ], '''FEAL''' (the '''Fast |
In ], '''FEAL''' (the '''Fast data Encipherment Algorithm''') is a ] proposed as an alternative to the ] (DES), and designed to be much faster in software. The ] based algorithm was first published in 1987 by ] and ] from ]. The cipher is susceptible to various forms of ], and has acted as a catalyst in the discovery of ] and ]. | ||
| There have been several different revisions of FEAL, though all are ]s, and make use of the same basic round function and operate on a ]. One of the earliest designs is now termed '''FEAL-4''', which has four rounds and a ]. | There have been several different revisions of FEAL, though all are ]s, and make use of the same basic round function and operate on a ]. One of the earliest designs is now termed '''FEAL-4''', which has four rounds and a ]. | ||
| <!-- den Boer refers to an earlier FEAL-1 and FEAL-2, and Gutmann also mentions pre-FEAL-4 versions, but info on these is hard to find, and they aren't significant, really --> | <!-- den Boer refers to an earlier FEAL-1 and FEAL-2, and Gutmann also mentions pre-FEAL-4 versions, but info on these is hard to find, and they aren't significant, really --> | ||
| Problems were found with FEAL-4 from the start: Bert den Boer related a weakness in an unpublished rump session at the same conference where the cipher was first presented. A later paper (den Boer, 1988) describes an attack requiring 100–10000 ]s, and Sean Murphy (1990) found an improvement that needs only 20 chosen plaintexts. Murphy and den Boer's methods contain elements similar to those used in ]. | |||
| The designers countered by doubling the number of rounds, '''FEAL-8''' (Shimizu and Miyaguchi, 1988). However, eight rounds also proved to be insufficient — in |
The designers countered by doubling the number of rounds, '''FEAL-8''' (Shimizu and Miyaguchi, 1988). However, eight rounds also proved to be insufficient — in 1989, at the Securicom conference, ] and ] described a differential attack on the cipher, mentioned in (Miyaguchi, 1989). Gilbert and Chassé (1990) subsequently published a statistical attack similar to differential cryptanalysis which requires 10000 pairs of chosen plaintexts. | ||
| In response, the designers introduced a variable-round cipher, '''FEAL-N''' (Miyaguchi, 1990), where "N" was chosen by the user, together with '''FEAL-NX''', which had a larger 128-bit key. Biham and Shamir's differential cryptanalysis (1991) showed that both FEAL-N and FEAL-NX could be broken faster than exhaustive search for N ≤ 31. Later attacks, precursors to linear cryptanalysis, could break versions under the ] assumption, first (Tardy-Corfdir and Gilbert, 1991) and then (Matsui and Yamagishi, 1992), the latter breaking FEAL-4 with 5 known plaintexts, FEAL-6 with 100, and FEAL-8 with 2<sup>15</sup>. | In response, the designers introduced a variable-round cipher, '''FEAL-N''' (Miyaguchi, 1990), where "N" was chosen by the user, together with '''FEAL-NX''', which had a larger 128-bit key. Biham and Shamir's differential cryptanalysis (1991) showed that both FEAL-N and FEAL-NX could be broken faster than exhaustive search for N ≤ 31. Later attacks, precursors to linear cryptanalysis, could break versions under the ] assumption, first (Tardy-Corfdir and Gilbert, 1991) and then (Matsui and Yamagishi, 1992), the latter breaking FEAL-4 with 5 known plaintexts, FEAL-6 with 100, and FEAL-8 with 2<sup>15</sup>. | ||
| In 1994, Ohta and Aoki presented a linear cryptanalytic attack against FEAL-8 that required 2<sup>12</sup> known plaintexts.<ref>{{cite web|url=http://x5.net/faqs/crypto/q79.html |title=Q79: What is FEAL? |publisher=X5.net |access-date=2013-02-19}}</ref> | |||
| ==See also== | ==See also== | ||
| * ] | * ] | ||
| ==Notes== | |||
| {{reflist}} | |||
| ==References== | ==References== | ||
| Line 42: | Line 47: | ||
| ==External links== | ==External links== | ||
| * | * | ||
| * | * | ||
| * | * {{Webarchive|url=https://web.archive.org/web/20160409112249/http://patft.uspto.gov/netacgi/nph-Parser?TERM1=4850019&u=/netahtml/srchnum.htm&Sect1=PTO1&Sect2=HITOFF&p=1&r=0&l=50&f=S&d=PALL |date=2016-04-09 }} | ||
| ⚫ | {{ |
||
| ⚫ | {{Cryptography navbox | block}} | ||
| ⚫ | ] | ||
| ] | |||
| ] | |||
| ⚫ | ] | ||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 01:40, 17 October 2023
Block cipher| This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2015) (Learn how and when to remove this message) |
 | |
| General | |
|---|---|
| Designers | Akihiro Shimizu and Shoji Miyaguchi (NTT) |
| First published | FEAL-4 in 1987; FEAL-N/NX in 1990 |
| Cipher detail | |
| Key sizes | 64 bits (FEAL), 128 bits (FEAL-NX) |
| Block sizes | 64 bits |
| Structure | Feistel network |
| Rounds | Originally 4, then 8, then variable (recommended 32) |
| Best public cryptanalysis | |
| Linear cryptanalysis can break FEAL-4 with 5 known plaintexts (Matsui and Yamagishi, 1992). A differential attack breaks FEAL-N/NX with fewer than 31 rounds (Biham and Shamir, 1991). | |
In cryptography, FEAL (the Fast data Encipherment Algorithm) is a block cipher proposed as an alternative to the Data Encryption Standard (DES), and designed to be much faster in software. The Feistel based algorithm was first published in 1987 by Akihiro Shimizu and Shoji Miyaguchi from NTT. The cipher is susceptible to various forms of cryptanalysis, and has acted as a catalyst in the discovery of differential and linear cryptanalysis.
There have been several different revisions of FEAL, though all are Feistel ciphers, and make use of the same basic round function and operate on a 64-bit block. One of the earliest designs is now termed FEAL-4, which has four rounds and a 64-bit key.
Problems were found with FEAL-4 from the start: Bert den Boer related a weakness in an unpublished rump session at the same conference where the cipher was first presented. A later paper (den Boer, 1988) describes an attack requiring 100–10000 chosen plaintexts, and Sean Murphy (1990) found an improvement that needs only 20 chosen plaintexts. Murphy and den Boer's methods contain elements similar to those used in differential cryptanalysis.
The designers countered by doubling the number of rounds, FEAL-8 (Shimizu and Miyaguchi, 1988). However, eight rounds also proved to be insufficient — in 1989, at the Securicom conference, Eli Biham and Adi Shamir described a differential attack on the cipher, mentioned in (Miyaguchi, 1989). Gilbert and Chassé (1990) subsequently published a statistical attack similar to differential cryptanalysis which requires 10000 pairs of chosen plaintexts.
In response, the designers introduced a variable-round cipher, FEAL-N (Miyaguchi, 1990), where "N" was chosen by the user, together with FEAL-NX, which had a larger 128-bit key. Biham and Shamir's differential cryptanalysis (1991) showed that both FEAL-N and FEAL-NX could be broken faster than exhaustive search for N ≤ 31. Later attacks, precursors to linear cryptanalysis, could break versions under the known plaintext assumption, first (Tardy-Corfdir and Gilbert, 1991) and then (Matsui and Yamagishi, 1992), the latter breaking FEAL-4 with 5 known plaintexts, FEAL-6 with 100, and FEAL-8 with 2.
In 1994, Ohta and Aoki presented a linear cryptanalytic attack against FEAL-8 that required 2 known plaintexts.
See also
Notes
- "Q79: What is FEAL?". X5.net. Retrieved 2013-02-19.
References
- Eli Biham, Adi Shamir: Differential Cryptanalysis of Feal and N-Hash. EUROCRYPT 1991: 1–16
- Bert den Boer, Cryptanalysis of F.E.A.L., EUROCRYPT 1988: 293–299
- Henri Gilbert, Guy Chassé: A Statistical Attack of the FEAL-8 Cryptosystem. CRYPTO 1990: 22–33.
- Shoji Miyaguchi: The FEAL Cipher Family. CRYPTO 1990: 627–638
- Shoji Miyaguchi: The FEAL-8 Cryptosystem and a Call for Attack. CRYPTO 1989: 624–627
- Mitsuru Matsui, Atsuhiro Yamagishi: A New Method for Known Plaintext Attack of FEAL Cipher. EUROCRYPT 1992: 81–91
- Sean Murphy, The Cryptanalysis of FEAL-4 with 20 Chosen Plaintexts. J. Cryptology 2(3): 145–154 (1990)
- A. Shimizu and S. Miyaguchi, Fast data encipherment algorithm FEAL, Advances in Cryptology — Eurocrypt '87, Springer-Verlag (1988), 267–280.
- Anne Tardy-Corfdir, Henri Gilbert: A Known Plaintext Attack of FEAL-4 and FEAL-6. CRYPTO 1991: 172–181
External links
- The FEAL home page
- A sci.crypt article by Peter Gutmann describing FEAL
- US patent 4850019 Archived 2016-04-09 at the Wayback Machine