| Revision as of 16:09, 14 March 2023 editXOR'easter (talk | contribs)Extended confirmed users32,681 edits more wranglingTag: Visual edit: Switched← Previous edit | Latest revision as of 01:07, 21 December 2024 edit undoStarryGrandma (talk | contribs)Extended confirmed users14,624 edits Restored revision 1183282109 by EditingPencil (talk): Removing the pi, units are stated as per steradianTags: Twinkle Undo | ||
| (24 intermediate revisions by 14 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Approximation of a black body's spectral radiance}} | {{Short description|Approximation of a black body's spectral radiance}} | ||
| {{Use American English|date = March 2019}} | {{Use American English|date = March 2019}} | ||
| ] and ], for a body of |
] and ], for a body of 5800 K ].]] | ||
| In ], the '''Rayleigh–Jeans law''' is an approximation to the ] of ] as a function of ] from a ] at a given temperature through classical arguments. For wavelength λ, it is |
In ], the '''Rayleigh–Jeans law''' is an approximation to the ] of ] as a function of ] from a ] at a given temperature through classical arguments. For wavelength ''λ'', it is | ||
| <math display="block">B_ |
<math display="block"> | ||
| B_\lambda(T) = \frac{2ck_\text{B}T}{\lambda^4}, | |||
| </math> | |||
| where <math>B_ |
where <math>B_\lambda</math> is the ] (the power emitted per unit emitting area, per ], per unit wavelength), <math>c</math> is the ], <math>k_\text{B}</math> is the ], and <math>T</math> is the ] in ]s. For ] <math>\nu</math>, the expression is instead | ||
| <math display="block">B_ |
<math display="block"> | ||
| B_\nu(T) = \frac{2 \nu^2 k_\text{B} T}{c^2}. | |||
| </math> | |||
| The Rayleigh–Jeans law agrees with experimental results at large wavelengths (low frequencies) but strongly disagrees at short wavelengths (high frequencies). This inconsistency between observations and the predictions of ] is commonly known as the ].<ref name="auto">{{cite book |title=Astronomy: A Physical Perspective |first=Mark L. |last=Kutner |publisher=Cambridge University Press |year=2003 |isbn=0-521-52927-1 |page= |url=https://archive.org/details/astronomyphysica00kutn/page/15 }}</ref><ref>{{cite book |title=Radiative Processes in Astrophysics | |
The Rayleigh–Jeans law agrees with experimental results at large wavelengths (low frequencies) but strongly disagrees at short wavelengths (high frequencies). This inconsistency between observations and the predictions of ] is commonly known as the ].<ref name="auto">{{cite book |title=Astronomy: A Physical Perspective |first=Mark L. |last=Kutner |publisher=Cambridge University Press |year=2003 |isbn=0-521-52927-1 |page= |url=https://archive.org/details/astronomyphysica00kutn/page/15 }}</ref><ref>{{cite book |title=Radiative Processes in Astrophysics |last1=Rybicki |last2=Lightman |publisher=Wiley |year=2004 |pages=20–28 |isbn=0-471-82759-2 }}</ref> ], which gives the correct radiation at all frequencies, has the Rayleigh–Jeans law as its low-frequency limit. | ||
| ==Historical development== | == Historical development == | ||
| In 1900, the British physicist ] derived the ''λ''<sup>−4</sup> dependence of the Rayleigh–Jeans law based on classical physical arguments, relying upon the ]. This law predicted an energy output that diverges towards ] as wavelength approaches zero (as frequency tends to infinity). Measurements of the spectral emission of actual black bodies revealed that the emission agreed with Rayleigh's calculation at low frequencies but diverged at high frequencies |
In 1900, the British physicist ] derived the ''λ''<sup>−4</sup> dependence of the Rayleigh–Jeans law based on classical physical arguments, relying upon the ]. This law predicted an energy output that diverges towards ] as wavelength approaches zero (as frequency tends to infinity). Measurements of the spectral emission of actual black bodies revealed that the emission agreed with Rayleigh's calculation at low frequencies but diverged at high frequencies, reaching a maximum and then falling with frequency, so the total energy emitted is finite. Rayleigh recognized the unphysical behavior of his formula at high frequencies and introduced an ''ad hoc'' cutoff to correct it, but experimentalists found that his cutoff did not agree with data.<ref name="auto"/><ref name=":0">{{Cite journal |last=Pais |first=A. |date=1979-10-01 |title=Einstein and the quantum theory |url=https://link.aps.org/doi/10.1103/RevModPhys.51.863 |journal=Reviews of Modern Physics |language=en |volume=51 |issue=4 |pages=863–914 |doi=10.1103/RevModPhys.51.863 |bibcode=1979RvMP...51..863P |issn=0034-6861}}</ref> ] also presented a derivation of the wavelength dependence in 1903. More complete derivations, which included the proportionality constant, were presented in 1905 by Rayleigh and Sir ] and independently by ].<ref name=":0" /> Rayleigh believed that this discrepancy could be resolved by the equipartition theorem failing to be valid for high-frequency vibrations, while Jeans argued that the underlying cause was matter and ] not being in thermal equilibrium.<ref name=":0" /> | ||
| Rayleigh published his first derivation of the frequency dependence in June 1900. Planck discovered the curve now known as Planck's law in October of that year and presented it in December.<ref name=":0" /> Planck's original intent was to find a satisfactory derivation of ] for the blackbody radiation curve, which accurately described the data at high frequencies. Planck found Wien's original derivation inadequate and devised his own. Then, after learning that the most recent experimental results disagreed with his predictions for low frequencies, Planck revised his calculation, obtaining what is now called Planck's law.<ref>{{cite journal|last=Kragh|first=H. |year=2000 |title=Max Planck: the reluctant revolutionary |journal=Physics World |volume=13 |number=12 |pages=31–36 |doi=10.1088/2058-7058/13/12/34}}</ref> | Rayleigh published his first derivation of the frequency dependence in June 1900. Planck discovered the curve now known as Planck's law in October of that year and presented it in December.<ref name=":0" /> Planck's original intent was to find a satisfactory derivation of ] for the blackbody radiation curve, which accurately described the data at high frequencies. Planck found Wien's original derivation inadequate and devised his own. Then, after learning that the most recent experimental results disagreed with his predictions for low frequencies, Planck revised his calculation, obtaining what is now called Planck's law.<ref>{{cite journal |last=Kragh |first=H. |year=2000 |title=Max Planck: the reluctant revolutionary |journal=Physics World |volume=13 |number=12 |pages=31–36 |doi=10.1088/2058-7058/13/12/34}}</ref> | ||
| ==Comparison to Planck's law== | == Comparison to Planck's law == | ||
| In 1900 ] empirically obtained an expression for ] expressed in terms of wavelength {{nowrap|1=''λ'' = ''c''/''ν''}} (]): | In 1900 ] empirically obtained an expression for ] expressed in terms of wavelength {{nowrap|1=''λ'' = ''c''/''ν''}} (]): | ||
| <math display="block">B_\lambda(T) = \frac{ |
<math display="block"> | ||
| B_\lambda(T) = \frac{2hc^2}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda k_\text{B} T} - 1}, | |||
| </math> | |||
| where ''h'' is the ] and {{math|''k''<sub>B</sub>}} the ]. |
where ''h'' is the ], and {{math|''k''<sub>B</sub>}} is the ]. Planck's law does not suffer from an ultraviolet catastrophe and agrees well with the experimental data, but its full significance (which ultimately led to quantum theory) was only appreciated several years later. Since | ||
| <math display="block">e^x = 1 + x + {x^2 |
<math display="block"> | ||
| e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots, | |||
| </math> | |||
| then in the limit of high temperatures or long wavelengths, the term in the exponential becomes small, and the exponential is well approximated with the ] first-order term |
then in the limit of high temperatures or long wavelengths, the term in the exponential becomes small, and the exponential is well approximated with the ] first-order term: | ||
| <math display="block">e^{\frac{hc}{\lambda k_\ |
<math display="block"> | ||
| e^{\frac{hc}{\lambda k_\text{B} T}} \approx 1 + \frac{hc}{\lambda k_\text{B} T}. | |||
| </math> | |||
| So |
So | ||
| <math display="block">\frac{1}{e^\frac{hc}{\lambda k_\ |
<math display="block"> | ||
| \frac{1}{e^\frac{hc}{\lambda k_\text{B} T} - 1} \approx \frac{1}{\frac{hc}{\lambda k_\text{B} T}} = \frac{\lambda k_\text{B} T}{hc}. | |||
| </math> | |||
| This results in Planck's blackbody formula reducing to | This results in Planck's blackbody formula reducing to | ||
| <math display="block">B_{\lambda}(T) = \frac{2 ck_\ |
<math display="block"> | ||
| B_{\lambda}(T) = \frac{2 ck_\text{B} T}{\lambda^4}, | |||
| </math> | |||
| which is identical to the classically derived Rayleigh–Jeans expression. | which is identical to the classically derived Rayleigh–Jeans expression. | ||
| The same argument can be applied to the blackbody radiation expressed in terms of frequency {{nowrap|1=''ν'' = ''c''/''λ''}}. In the limit of small frequencies, that is <math> h \nu \ll k_\ |
The same argument can be applied to the blackbody radiation expressed in terms of frequency {{nowrap|1=''ν'' = ''c''/''λ''}}. In the limit of small frequencies, that is <math> h \nu \ll k_\text{B} T </math>, | ||
| <math display="block">B_\nu(T) = \frac{2 h\nu^3}{c^2}\frac{1}{e^\frac{h\nu}{k_\ |
<math display="block"> | ||
| B_\nu(T) = \frac{2 h\nu^3}{c^2} \frac{1}{e^\frac{h\nu}{k_\text{B} T} - 1} \approx \frac{2 h\nu^3}{c^2} \cdot \frac{k_\text{B} T}{h\nu} = \frac{2 \nu^2 k_\mathrm{B} T}{c^2}. | |||
| </math> | |||
| This last expression is the Rayleigh–Jeans law in the limit of small frequencies. | This last expression is the Rayleigh–Jeans law in the limit of small frequencies. | ||
| ==Consistency of frequency and wavelength |
== Consistency of frequency- and wavelength-dependent expressions == | ||
| When comparing the frequency and wavelength |
When comparing the frequency- and wavelength-dependent expressions of the Rayleigh–Jeans law, it is important to remember that | ||
| <math display="block">\frac{dP}{d\lambda} = B_{\lambda}(T) |
<math display="block"> | ||
| \frac{dP}{d\lambda} = B_{\lambda}(T) | |||
| </math> | |||
| and | |||
| <math display="block">\frac{dP}{d\nu} = B_{\nu}(T)</math> | <math display="block"> | ||
| \frac{dP}{d\nu} = B_{\nu}(T). | |||
| </math> | |||
| Note that these two expressions then have different units, as a step <math>d\lambda</math> in wavelength is not equivalent to a step <math>d\nu</math> in frequency. Therefore, | |||
| Therefore, | |||
| <math display="block">B_{\lambda}(T) \neq B_{\nu}(T)</math> | <math display="block"> | ||
| B_{\lambda}(T) \neq B_{\nu}(T), | |||
| </math> | |||
| even after substituting the value <math>\lambda = c |
even after substituting the value <math>\lambda = c/\nu</math>, because <math>B_\lambda(T)</math> has units of energy emitted per unit time per unit area of emitting surface, per unit solid angle, ''per unit wavelength'', whereas <math>B_\nu(T)</math> has units of energy emitted per unit time per unit area of emitting surface, per unit solid angle, ''per unit frequency''. To be consistent, we must use the equality | ||
| <math display="block">B_ |
<math display="block"> | ||
| B_\lambda \, d\lambda = dP = B_\nu \, d\nu, | |||
| </math> | |||
| where both sides now have units of power (energy emitted per unit time) per unit area of emitting surface, per unit solid angle. | where both sides now have units of power (energy emitted per unit time) per unit area of emitting surface, per unit solid angle. | ||
| Starting with the Rayleigh–Jeans law in terms of wavelength we get | Starting with the Rayleigh–Jeans law in terms of wavelength, we get | ||
| <math display="block">B_ |
<math display="block"> | ||
| B_\lambda(T) = B_\nu(T) \frac{d\nu}{d\lambda}, | |||
| </math> | |||
| where | where | ||
| <math display="block">\frac{d\nu}{d\lambda} = \frac{d}{d\lambda}\left(\frac{c}{\lambda}\right) = -\frac{c}{\lambda^2}.</math> | <math display="block"> | ||
| \frac{d\nu}{d\lambda} = \frac{d}{d\lambda} \left(\frac{c}{\lambda}\right) = -\frac{c}{\lambda^2}. | |||
| </math> | |||
| This leads |
This leads to | ||
| <math display="block">B_ |
<math display="block"> | ||
| B_\lambda(T) = \frac{2k_\text{B} T\left(\frac{c}{\lambda}\right)^2}{c^2} \times \frac{c}{\lambda^2} = \frac{2ck_\text{B} T}{\lambda^4}. | |||
| </math> | |||
| ==Other forms of Rayleigh–Jeans law== | == Other forms of Rayleigh–Jeans law == | ||
| Depending on the application, the Planck function can be expressed in 3 different forms. The first involves energy emitted per unit time per unit area of emitting surface, per unit solid angle, per spectral unit. In this form, the Planck function and associated Rayleigh–Jeans limits are given by | Depending on the application, the Planck function can be expressed in 3 different forms. The first involves energy emitted per unit time per unit area of emitting surface, per unit solid angle, per spectral unit. In this form, the Planck function and associated Rayleigh–Jeans limits are given by | ||
| <math display="block">B_\lambda(T) = \frac{2 hc^2}{\lambda^5} |
<math display="block"> | ||
| B_\lambda(T) = \frac{2 hc^2}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda k_\text{B} T} - 1} \approx \frac{2ck_\text{B} T}{\lambda^4} | |||
| </math> | |||
| or | or | ||
| <math display="block">B_\nu(T) = \frac{2h\nu^3}{c^2}\frac{1}{e^\frac{h\nu}{k_\ |
<math display="block"> | ||
| B_\nu(T) = \frac{2h\nu^3}{c^2} \frac{1}{e^\frac{h\nu}{k_\text{B} T} - 1} \approx \frac{2k_\text{B} T\nu^2}{c^2}. | |||
| </math> | |||
| Alternatively, Planck's law can be written as an expression <math>I(\nu,T) = \pi B_\nu(T)</math> for emitted power integrated over all solid angles. In this form, the Planck function and associated Rayleigh–Jeans limits are given by | Alternatively, Planck's law can be written as an expression <math>I(\nu, T) = \pi B_\nu(T)</math> for emitted power integrated over all solid angles. In this form, the Planck function and associated Rayleigh–Jeans limits are given by | ||
| <math display="block">I(\lambda,T) = |
<math display="block"> | ||
| I(\lambda, T) = \frac{2\pi hc^2}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda k_\text{B} T} - 1} \approx \frac{2\pi ck_\text{B} T}{\lambda^4} | |||
| </math> | |||
| or | or | ||
| <math display="block">I(\nu,T) = |
<math display="block"> | ||
| I(\nu, T) = \frac{2\pi h\nu^3}{c^2} \frac{1}{e^\frac{h\nu}{k_\text{B} T} - 1} \approx \frac{2 \pi k_\text{B} T\nu^2}{c^2}. | |||
| </math> | |||
| In other cases, Planck's law is written as |
In other cases, Planck's law is written as | ||
| <math display="inline"> | |||
| u(\nu, T) = \frac{4\pi}{c} B_\nu(T) | |||
| </math> | |||
| for energy per unit volume (energy density). In this form, the Planck function and associated Rayleigh–Jeans limits are given by | |||
| <math display="block">u(\lambda,T) = \frac{8 \pi hc}{\lambda^5} |
<math display="block"> | ||
| u(\lambda, T) = \frac{8 \pi hc}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda k_\text{B} T} - 1} \approx \frac{8\pi k_\text{B} T}{\lambda^4} | |||
| </math> | |||
| or | or | ||
| <math display="block">u(\nu,T) = \frac{8\pi h\nu^3}{c^3}\frac{1}{e^\frac{h\nu}{k_\ |
<math display="block"> | ||
| u(\nu, T) = \frac{8\pi h\nu^3}{c^3} \frac{1}{e^\frac{h\nu}{k_\text{B} T} - 1} \approx \frac{8 \pi k_\text{B} T\nu^2}{c^3}. | |||
| </math> | |||
| ==See also== | == See also == | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | |||
| * ] | * ] | ||
| ==References== | == References == | ||
| {{Reflist}} | {{Reflist}} | ||
| <!-- {{cite book |first= |last=Beiser |title=Concepts of Modern Physics |publisher=McGraw Hill Education |year= |isbn= }} --> | <!-- {{cite book |first= |last=Beiser |title=Concepts of Modern Physics |publisher=McGraw Hill Education |year= |isbn= }} --> | ||
| ==External links== | == External links == | ||
| * | * | ||
| * | * | ||
| {{DEFAULTSORT:Rayleigh-Jeans law}} | {{DEFAULTSORT:Rayleigh-Jeans law}} | ||
| ] | ] | ||
| ] | |||
Latest revision as of 01:07, 21 December 2024
Approximation of a black body's spectral radiance
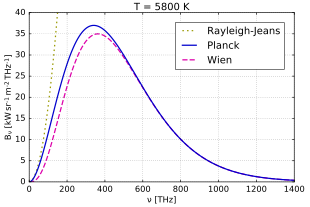
In physics, the Rayleigh–Jeans law is an approximation to the spectral radiance of electromagnetic radiation as a function of wavelength from a black body at a given temperature through classical arguments. For wavelength λ, it is where is the spectral radiance (the power emitted per unit emitting area, per steradian, per unit wavelength), is the speed of light, is the Boltzmann constant, and is the temperature in kelvins. For frequency , the expression is instead
The Rayleigh–Jeans law agrees with experimental results at large wavelengths (low frequencies) but strongly disagrees at short wavelengths (high frequencies). This inconsistency between observations and the predictions of classical physics is commonly known as the ultraviolet catastrophe. Planck's law, which gives the correct radiation at all frequencies, has the Rayleigh–Jeans law as its low-frequency limit.
Historical development
In 1900, the British physicist Lord Rayleigh derived the λ dependence of the Rayleigh–Jeans law based on classical physical arguments, relying upon the equipartition theorem. This law predicted an energy output that diverges towards infinity as wavelength approaches zero (as frequency tends to infinity). Measurements of the spectral emission of actual black bodies revealed that the emission agreed with Rayleigh's calculation at low frequencies but diverged at high frequencies, reaching a maximum and then falling with frequency, so the total energy emitted is finite. Rayleigh recognized the unphysical behavior of his formula at high frequencies and introduced an ad hoc cutoff to correct it, but experimentalists found that his cutoff did not agree with data. Hendrik Lorentz also presented a derivation of the wavelength dependence in 1903. More complete derivations, which included the proportionality constant, were presented in 1905 by Rayleigh and Sir James Jeans and independently by Albert Einstein. Rayleigh believed that this discrepancy could be resolved by the equipartition theorem failing to be valid for high-frequency vibrations, while Jeans argued that the underlying cause was matter and luminiferous aether not being in thermal equilibrium.
Rayleigh published his first derivation of the frequency dependence in June 1900. Planck discovered the curve now known as Planck's law in October of that year and presented it in December. Planck's original intent was to find a satisfactory derivation of Wien's expression for the blackbody radiation curve, which accurately described the data at high frequencies. Planck found Wien's original derivation inadequate and devised his own. Then, after learning that the most recent experimental results disagreed with his predictions for low frequencies, Planck revised his calculation, obtaining what is now called Planck's law.
Comparison to Planck's law
In 1900 Max Planck empirically obtained an expression for black-body radiation expressed in terms of wavelength λ = c/ν (Planck's law): where h is the Planck constant, and kB is the Boltzmann constant. Planck's law does not suffer from an ultraviolet catastrophe and agrees well with the experimental data, but its full significance (which ultimately led to quantum theory) was only appreciated several years later. Since then in the limit of high temperatures or long wavelengths, the term in the exponential becomes small, and the exponential is well approximated with the Taylor polynomial's first-order term:
So
This results in Planck's blackbody formula reducing to which is identical to the classically derived Rayleigh–Jeans expression.
The same argument can be applied to the blackbody radiation expressed in terms of frequency ν = c/λ. In the limit of small frequencies, that is ,
This last expression is the Rayleigh–Jeans law in the limit of small frequencies.
Consistency of frequency- and wavelength-dependent expressions
When comparing the frequency- and wavelength-dependent expressions of the Rayleigh–Jeans law, it is important to remember that and Note that these two expressions then have different units, as a step in wavelength is not equivalent to a step in frequency. Therefore, even after substituting the value , because has units of energy emitted per unit time per unit area of emitting surface, per unit solid angle, per unit wavelength, whereas has units of energy emitted per unit time per unit area of emitting surface, per unit solid angle, per unit frequency. To be consistent, we must use the equality where both sides now have units of power (energy emitted per unit time) per unit area of emitting surface, per unit solid angle.
Starting with the Rayleigh–Jeans law in terms of wavelength, we get where This leads to
Other forms of Rayleigh–Jeans law
Depending on the application, the Planck function can be expressed in 3 different forms. The first involves energy emitted per unit time per unit area of emitting surface, per unit solid angle, per spectral unit. In this form, the Planck function and associated Rayleigh–Jeans limits are given by or
Alternatively, Planck's law can be written as an expression for emitted power integrated over all solid angles. In this form, the Planck function and associated Rayleigh–Jeans limits are given by or
In other cases, Planck's law is written as for energy per unit volume (energy density). In this form, the Planck function and associated Rayleigh–Jeans limits are given by or
See also
References
- ^ Kutner, Mark L. (2003). Astronomy: A Physical Perspective. Cambridge University Press. p. 15. ISBN 0-521-52927-1.
- Rybicki; Lightman (2004). Radiative Processes in Astrophysics. Wiley. pp. 20–28. ISBN 0-471-82759-2.
- ^ Pais, A. (1979-10-01). "Einstein and the quantum theory". Reviews of Modern Physics. 51 (4): 863–914. Bibcode:1979RvMP...51..863P. doi:10.1103/RevModPhys.51.863. ISSN 0034-6861.
- Kragh, H. (2000). "Max Planck: the reluctant revolutionary". Physics World. 13 (12): 31–36. doi:10.1088/2058-7058/13/12/34.
 where
where  is the
is the  is the
is the  is the
is the  is the
is the  , the expression is instead
, the expression is instead

 where h is the
where h is the  then in the limit of high temperatures or long wavelengths, the term in the exponential becomes small, and the exponential is well approximated with the
then in the limit of high temperatures or long wavelengths, the term in the exponential becomes small, and the exponential is well approximated with the 

 ,
,

 and
and
 Note that these two expressions then have different units, as a step
Note that these two expressions then have different units, as a step  in wavelength is not equivalent to a step
in wavelength is not equivalent to a step  in frequency. Therefore,
in frequency. Therefore,
 even after substituting the value
even after substituting the value  , because
, because  has units of energy emitted per unit time per unit area of emitting surface, per unit solid angle, per unit wavelength, whereas
has units of energy emitted per unit time per unit area of emitting surface, per unit solid angle, per unit wavelength, whereas  has units of energy emitted per unit time per unit area of emitting surface, per unit solid angle, per unit frequency. To be consistent, we must use the equality
has units of energy emitted per unit time per unit area of emitting surface, per unit solid angle, per unit frequency. To be consistent, we must use the equality
 where both sides now have units of power (energy emitted per unit time) per unit area of emitting surface, per unit solid angle.
where both sides now have units of power (energy emitted per unit time) per unit area of emitting surface, per unit solid angle.
 where
where
 This leads to
This leads to

 or
or

 for emitted power integrated over all solid angles. In this form, the Planck function and associated Rayleigh–Jeans limits are given by
for emitted power integrated over all solid angles. In this form, the Planck function and associated Rayleigh–Jeans limits are given by
 or
or

 for energy per unit volume (energy density). In this form, the Planck function and associated Rayleigh–Jeans limits are given by
for energy per unit volume (energy density). In this form, the Planck function and associated Rayleigh–Jeans limits are given by
 or
or
