| Revision as of 14:46, 22 September 2024 edit2409:40e0:1058:2941:8000:: (talk)No edit summaryTags: Visual edit Mobile edit Mobile web edit← Previous edit | Latest revision as of 12:43, 22 October 2024 edit undoDirac66 (talk | contribs)Extended confirmed users17,936 edits For oxygen, compare with valence bond theory, not with VSEPR which does not deal with diatomic molecules. | ||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 4: | Line 4: | ||
| {{Electronic structure methods}} | {{Electronic structure methods}} | ||
| In ], '''molecular orbital theory''' (MO theory or MOT) is a method for describing the electronic structure of molecules using ]. It was proposed early in the 20th century. The MOT |
In ], '''molecular orbital theory''' (MO theory or MOT) is a method for describing the electronic structure of molecules using ]. It was proposed early in the 20th century. The MOT explains the ] nature of ], which ] cannot explain. | ||
| In molecular orbital theory, ]s in a molecule are not assigned to individual ]s between ]s, but are treated as moving under the influence of the ] in the whole molecule.<ref>{{cite book|author=Daintith, J. |title=Oxford Dictionary of Chemistry|location=New York | publisher=Oxford University Press|year=2004|isbn=978-0-19-860918-6}}</ref> Quantum mechanics describes the spatial and energetic properties of electrons as molecular orbitals that surround two or more atoms in a molecule and contain ]s between atoms. | In molecular orbital theory, ]s in a molecule are not assigned to individual ]s between ]s, but are treated as moving under the influence of the ] in the whole molecule.<ref>{{cite book|author=Daintith, J. |title=Oxford Dictionary of Chemistry|location=New York | publisher=Oxford University Press|year=2004|isbn=978-0-19-860918-6}}</ref> Quantum mechanics describes the spatial and energetic properties of electrons as molecular orbitals that surround two or more atoms in a molecule and contain ]s between atoms. | ||
| Molecular orbital theory revolutionized the study of chemical bonding by approximating the states of bonded |
Molecular orbital theory revolutionized the study of chemical bonding by approximating the states of bonded electrons – the molecular orbitals – as ] (LCAO). These approximations are made by applying the ] (DFT) or ] (HF) models to the ]. | ||
| Molecular orbital theory and ] are the foundational theories of ]. | Molecular orbital theory and ] are the foundational theories of ]. | ||
| ==Linear combination of atomic orbitals (LCAO) method |
==Linear combination of atomic orbitals (LCAO) method== | ||
| In the ] method, each molecule has a set of ]s. It is assumed that the molecular orbital ] ''ψ<sub>j</sub>'' can be written as a simple weighted sum of the ''n'' constituent ]s ''χ<sub>i</sub>'', according to the following equation:<ref>{{cite book | author=Licker, Mark, J. |title=McGraw-Hill Concise Encyclopedia of Chemistry | location=New York | publisher=McGraw-Hill| year=2004 | isbn=978-0-07-143953-4}}</ref> | In the ] method, each molecule has a set of ]s. It is assumed that the molecular orbital ] ''ψ<sub>j</sub>'' can be written as a simple weighted sum of the ''n'' constituent ]s ''χ<sub>i</sub>'', according to the following equation:<ref>{{cite book | author=Licker, Mark, J. |title=McGraw-Hill Concise Encyclopedia of Chemistry | location=New York | publisher=McGraw-Hill| year=2004 | isbn=978-0-07-143953-4}}</ref> | ||
| <math display="block"> \psi_j = \sum_{i=1}^{n} c_{ij} \chi_i.</math> | <math display="block"> \psi_j = \sum_{i=1}^{n} c_{ij} \chi_i.</math> | ||
| One may determine ''c<sub>ij</sub>'' coefficients numerically by substituting this equation into the ] and applying the ]. The variational principle is a mathematical technique used in quantum mechanics to build up the coefficients of each atomic orbital basis. A larger coefficient means that the orbital basis is composed more of that particular contributing atomic |
One may determine ''c<sub>ij</sub>'' coefficients numerically by substituting this equation into the ] and applying the ]. The variational principle is a mathematical technique used in quantum mechanics to build up the coefficients of each atomic orbital basis. A larger coefficient means that the orbital basis is composed more of that particular contributing atomic orbital – hence, the molecular orbital is best characterized by that type. This method of quantifying orbital contribution as a ] is used in ]. An additional ] can be applied on the system to accelerate the convergence in some computational schemes. Molecular orbital theory was seen as a competitor to ] in the 1930s, before it was realized that the two methods are closely related and that when extended they become equivalent. | ||
| Molecular orbital theory is used to interpret ] ( |
Molecular orbital theory is used to interpret ] (UV–VIS). Changes to the electronic structure of molecules can be seen by the absorbance of light at specific wavelengths. Assignments can be made to these signals indicated by the transition of electrons moving from one orbital at a lower energy to a higher energy orbital. The molecular orbital diagram for the final state describes the electronic nature of the molecule in an excited state. | ||
| There are three main requirements for atomic orbital combinations to be suitable as approximate molecular orbitals. | There are three main requirements for atomic orbital combinations to be suitable as approximate molecular orbitals. | ||
| Line 46: | Line 46: | ||
| Common bonding orbitals are ] which are symmetric about the bond axis and ] with a ] along the bond axis. Less common are ] and ] with two and three nodal planes respectively along the bond axis. Antibonding orbitals are signified by the addition of an asterisk. For example, an antibonding pi orbital may be shown as π*. | Common bonding orbitals are ] which are symmetric about the bond axis and ] with a ] along the bond axis. Less common are ] and ] with two and three nodal planes respectively along the bond axis. Antibonding orbitals are signified by the addition of an asterisk. For example, an antibonding pi orbital may be shown as π*. | ||
| == Bond |
== Bond order == | ||
| ] | ] | ||
| Bond order is the number of chemical bonds between a pair of atoms. The bond order of a molecule can be calculated by subtracting the number of electrons in ] orbitals from the number of ] orbitals, and the resulting number is then divided by two. A molecule is expected to be stable if it has bond order larger than zero. It is adequate to consider the ] to determine the bond order. Because (for ] |
Bond order is the number of chemical bonds between a pair of atoms. The bond order of a molecule can be calculated by subtracting the number of electrons in ] orbitals from the number of ] orbitals, and the resulting number is then divided by two. A molecule is expected to be stable if it has bond order larger than zero. It is adequate to consider the ] to determine the bond order. Because (for ] ''n'' > 1) when MOs are derived from 1s AOs, the difference in number of electrons in bonding and anti-bonding molecular orbital is zero. So, there is no net effect on bond order if the electron is not the valence one. | ||
| <math>\text{Bond order} = \frac12 (\text{Number of electrons in bonding MO} - \text{Number of electrons in anti-bonding MO})</math> | |||
| From bond order, one can predict whether a bond between two atoms will form or not. For example, the existence of He<sub>2</sub> molecule. From the molecular orbital diagram, bond order |
From bond order, one can predict whether a bond between two atoms will form or not. For example, the existence of He<sub>2</sub> molecule. From the molecular orbital diagram, the bond order is <math display=inline>\frac12(2-2)=0</math>. That means, no bond formation will occur between two He atoms which is seen experimentally. It can be detected under very low temperature and pressure molecular beam and has ] of approximately 0.001 J/mol.<ref>{{Cite book |last1=Miessler |first1=Gary L. |url=https://books.google.com/books?id=VSktAAAAQBAJ |title=Inorganic Chemistry |last2=Fischer |first2=Paul J. |last3=Tarr |first3=Donald A. |date=2013-04-08 |publisher=Pearson Education |isbn=978-0-321-91779-9 |language=en}}</ref> | ||
| Besides, the strength of a bond can also be realized from bond order (BO). For example: | Besides, the strength of a bond can also be realized from bond order (BO). For example: | ||
| H<sub>2</sub> |
For H<sub>2</sub>: Bond order is <math display=inline>\frac12(2-0)=1</math>; bond energy is 436 kJ/mol. | ||
| H<sub>2</sub><sup>+</sup> |
For H<sub>2</sub><sup>+</sup>: Bond order is <math display=inline>\frac12(1-0)=\frac12</math>; bond energy is 171 kJ/mol. | ||
| As bond order of H<sub>2</sub><sup>+</sup> |
As the bond order of H<sub>2</sub><sup>+</sup> is smaller than H<sub>2</sub>, it should be less stable which is observed experimentally and can be seen from the bond energy. | ||
| ==Overview== | ==Overview== | ||
| {{more citations needed section|date=September 2020}} | {{more citations needed section|date=September 2020}} | ||
| MOT provides a global, delocalized perspective on ]. In MO theory, ''any'' electron in a molecule may be found ''anywhere'' in the molecule, since quantum conditions allow electrons to travel under the influence of an arbitrarily large number of nuclei, as long as they are in eigenstates permitted by certain quantum rules. Thus, when excited with the requisite amount of energy through high-frequency light or other means, electrons can transition to higher-energy molecular orbitals. For instance, in the simple case of a hydrogen diatomic molecule, promotion of a single electron from a bonding orbital to an antibonding orbital can occur under UV radiation. This promotion weakens the bond between the two hydrogen atoms and can lead to |
MOT provides a global, delocalized perspective on ]. In MO theory, ''any'' electron in a molecule may be found ''anywhere'' in the molecule, since quantum conditions allow electrons to travel under the influence of an arbitrarily large number of nuclei, as long as they are in eigenstates permitted by certain quantum rules. Thus, when excited with the requisite amount of energy through high-frequency light or other means, electrons can transition to higher-energy molecular orbitals. For instance, in the simple case of a hydrogen diatomic molecule, promotion of a single electron from a bonding orbital to an antibonding orbital can occur under UV radiation. This promotion weakens the bond between the two hydrogen atoms and can lead to photodissociation, the breaking of a chemical bond due to the absorption of light. | ||
| Molecular orbital theory is used to interpret ] ( |
Molecular orbital theory is used to interpret ] (UV–VIS). Changes to the electronic structure of molecules can be seen by the absorbance of light at specific wavelengths. Assignments can be made to these signals indicated by the transition of electrons moving from one orbital at a lower energy to a higher energy orbital. The molecular orbital diagram for the final state describes the electronic nature of the molecule in an excited state. | ||
| Although in MO theory ''some'' molecular orbitals may hold electrons that are more localized between specific pairs of molecular atoms, ''other'' orbitals may hold electrons that are spread more uniformly over the molecule. Thus, overall, bonding is far more delocalized in MO theory, which makes it more applicable to resonant molecules that have equivalent non-integer bond orders than ]. This makes MO theory more useful for the description of extended systems. | Although in MO theory ''some'' molecular orbitals may hold electrons that are more localized between specific pairs of molecular atoms, ''other'' orbitals may hold electrons that are spread more uniformly over the molecule. Thus, overall, bonding is far more delocalized in MO theory, which makes it more applicable to resonant molecules that have equivalent non-integer bond orders than ]. This makes MO theory more useful for the description of extended systems. | ||
| ], who actively participated in the advent of molecular orbital theory, considers each molecule to be a self-sufficient unit. He asserts in his article: <blockquote>...Attempts to regard a molecule as consisting of specific atomic or ionic units held together by discrete numbers of bonding electrons or electron-pairs are considered as more or less meaningless, except as an approximation in special cases, or as a method of calculation . A molecule is here regarded as a set of nuclei, around each of which is grouped an electron configuration closely similar to that of a free atom in an external field, except that the outer parts of the electron configurations surrounding each nucleus usually belong, in part, jointly to two or more nuclei....<ref>{{Cite journal|last=Mulliken|first=R. S.|date=October 1955|title=Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I|url=http://dx.doi.org/10.1063/1.1740588|journal=The Journal of Chemical Physics|volume=23|issue=10|pages=1833–1840|doi=10.1063/1.1740588|bibcode=1955JChPh..23.1833M |issn=0021-9606}}</ref></blockquote>An example is the MO description of ], {{chem|C|6|H|6}}, which is an aromatic hexagonal ring of six carbon atoms and three double bonds. In this molecule, 24 of the 30 total valence bonding |
], who actively participated in the advent of molecular orbital theory, considers each molecule to be a self-sufficient unit. He asserts in his article: <blockquote>...Attempts to regard a molecule as consisting of specific atomic or ionic units held together by discrete numbers of bonding electrons or electron-pairs are considered as more or less meaningless, except as an approximation in special cases, or as a method of calculation . A molecule is here regarded as a set of nuclei, around each of which is grouped an electron configuration closely similar to that of a free atom in an external field, except that the outer parts of the electron configurations surrounding each nucleus usually belong, in part, jointly to two or more nuclei....<ref>{{Cite journal|last=Mulliken|first=R. S.|date=October 1955|title=Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I|url=http://dx.doi.org/10.1063/1.1740588|journal=The Journal of Chemical Physics|volume=23|issue=10|pages=1833–1840|doi=10.1063/1.1740588|bibcode=1955JChPh..23.1833M |issn=0021-9606}}</ref></blockquote>An example is the MO description of ], {{chem|C|6|H|6}}, which is an aromatic hexagonal ring of six carbon atoms and three double bonds. In this molecule, 24 of the 30 total valence bonding electrons – 24 coming from carbon atoms and 6 coming from hydrogen atoms – are located in 12 σ (sigma) bonding orbitals, which are located mostly between pairs of atoms (C–C or C–H), similarly to the electrons in the valence bond description. However, in benzene the remaining six bonding electrons are located in three π (pi) molecular bonding orbitals that are delocalized around the ring. Two of these electrons are in an MO that has equal orbital contributions from all six atoms. The other four electrons are in orbitals with vertical nodes at right angles to each other. As in the VB theory, all of these six delocalized π electrons reside in a larger space that exists above and below the ring plane. All carbon–carbon bonds in benzene are chemically equivalent. In MO theory this is a direct consequence of the fact that the three molecular π orbitals combine and evenly spread the extra six electrons over six carbon atoms. | ||
| ] | ] | ||
| Line 90: | Line 90: | ||
| *] | *] | ||
| *] | *] | ||
| *] | |||
| {{colend}} | {{colend}} | ||
Latest revision as of 12:43, 22 October 2024
Method for describing the electronic structure of molecules using quantum mechanics See also: Molecular orbital
In chemistry, molecular orbital theory (MO theory or MOT) is a method for describing the electronic structure of molecules using quantum mechanics. It was proposed early in the 20th century. The MOT explains the paramagnetic nature of O2, which valence bond theory cannot explain.
In molecular orbital theory, electrons in a molecule are not assigned to individual chemical bonds between atoms, but are treated as moving under the influence of the atomic nuclei in the whole molecule. Quantum mechanics describes the spatial and energetic properties of electrons as molecular orbitals that surround two or more atoms in a molecule and contain valence electrons between atoms.
Molecular orbital theory revolutionized the study of chemical bonding by approximating the states of bonded electrons – the molecular orbitals – as linear combinations of atomic orbitals (LCAO). These approximations are made by applying the density functional theory (DFT) or Hartree–Fock (HF) models to the Schrödinger equation.
Molecular orbital theory and valence bond theory are the foundational theories of quantum chemistry.
Linear combination of atomic orbitals (LCAO) method
In the LCAO method, each molecule has a set of molecular orbitals. It is assumed that the molecular orbital wave function ψj can be written as a simple weighted sum of the n constituent atomic orbitals χi, according to the following equation:
One may determine cij coefficients numerically by substituting this equation into the Schrödinger equation and applying the variational principle. The variational principle is a mathematical technique used in quantum mechanics to build up the coefficients of each atomic orbital basis. A larger coefficient means that the orbital basis is composed more of that particular contributing atomic orbital – hence, the molecular orbital is best characterized by that type. This method of quantifying orbital contribution as a linear combination of atomic orbitals is used in computational chemistry. An additional unitary transformation can be applied on the system to accelerate the convergence in some computational schemes. Molecular orbital theory was seen as a competitor to valence bond theory in the 1930s, before it was realized that the two methods are closely related and that when extended they become equivalent.
Molecular orbital theory is used to interpret ultraviolet–visible spectroscopy (UV–VIS). Changes to the electronic structure of molecules can be seen by the absorbance of light at specific wavelengths. Assignments can be made to these signals indicated by the transition of electrons moving from one orbital at a lower energy to a higher energy orbital. The molecular orbital diagram for the final state describes the electronic nature of the molecule in an excited state.
There are three main requirements for atomic orbital combinations to be suitable as approximate molecular orbitals.
- The atomic orbital combination must have the correct symmetry, which means that it must belong to the correct irreducible representation of the molecular symmetry group. Using symmetry adapted linear combinations, or SALCs, molecular orbitals of the correct symmetry can be formed.
- Atomic orbitals must also overlap within space. They cannot combine to form molecular orbitals if they are too far away from one another.
- Atomic orbitals must be at similar energy levels to combine as molecular orbitals. Because if the energy difference is great, when the molecular orbitals form, the change in energy becomes small. Consequently, there is not enough reduction in energy of electrons to make significant bonding.
History
Molecular orbital theory was developed in the years after valence bond theory had been established (1927), primarily through the efforts of Friedrich Hund, Robert Mulliken, John C. Slater, and John Lennard-Jones. MO theory was originally called the Hund-Mulliken theory. According to physicist and physical chemist Erich Hückel, the first quantitative use of molecular orbital theory was the 1929 paper of Lennard-Jones. This paper predicted a triplet ground state for the dioxygen molecule which explained its paramagnetism (see Molecular orbital diagram § Dioxygen) before valence bond theory, which came up with its own explanation in 1931. The word orbital was introduced by Mulliken in 1932. By 1933, the molecular orbital theory had been accepted as a valid and useful theory.
Erich Hückel applied molecular orbital theory to unsaturated hydrocarbon molecules starting in 1931 with his Hückel molecular orbital (HMO) method for the determination of MO energies for pi electrons, which he applied to conjugated and aromatic hydrocarbons. This method provided an explanation of the stability of molecules with six pi-electrons such as benzene.
The first accurate calculation of a molecular orbital wavefunction was that made by Charles Coulson in 1938 on the hydrogen molecule. By 1950, molecular orbitals were completely defined as eigenfunctions (wave functions) of the self-consistent field Hamiltonian and it was at this point that molecular orbital theory became fully rigorous and consistent. This rigorous approach is known as the Hartree–Fock method for molecules although it had its origins in calculations on atoms. In calculations on molecules, the molecular orbitals are expanded in terms of an atomic orbital basis set, leading to the Roothaan equations. This led to the development of many ab initio quantum chemistry methods. In parallel, molecular orbital theory was applied in a more approximate manner using some empirically derived parameters in methods now known as semi-empirical quantum chemistry methods.
The success of Molecular Orbital Theory also spawned ligand field theory, which was developed during the 1930s and 1940s as an alternative to crystal field theory.
Types of orbitals
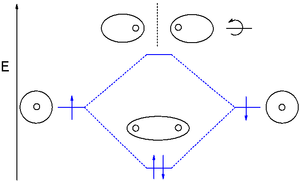
Molecular orbital (MO) theory uses a linear combination of atomic orbitals (LCAO) to represent molecular orbitals resulting from bonds between atoms. These are often divided into three types, bonding, antibonding, and non-bonding. A bonding orbital concentrates electron density in the region between a given pair of atoms, so that its electron density will tend to attract each of the two nuclei toward the other and hold the two atoms together. An anti-bonding orbital concentrates electron density "behind" each nucleus (i.e. on the side of each atom which is farthest from the other atom), and so tends to pull each of the two nuclei away from the other and actually weaken the bond between the two nuclei. Electrons in non-bonding orbitals tend to be associated with atomic orbitals that do not interact positively or negatively with one another, and electrons in these orbitals neither contribute to nor detract from bond strength.
Molecular orbitals are further divided according to the types of atomic orbitals they are formed from. Chemical substances will form bonding interactions if their orbitals become lower in energy when they interact with each other. Different bonding orbitals are distinguished that differ by electron configuration (electron cloud shape) and by energy levels.
The molecular orbitals of a molecule can be illustrated in molecular orbital diagrams.
Common bonding orbitals are sigma (σ) orbitals which are symmetric about the bond axis and pi (π) orbitals with a nodal plane along the bond axis. Less common are delta (δ) orbitals and phi (φ) orbitals with two and three nodal planes respectively along the bond axis. Antibonding orbitals are signified by the addition of an asterisk. For example, an antibonding pi orbital may be shown as π*.
Bond order
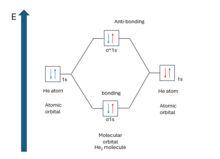
Bond order is the number of chemical bonds between a pair of atoms. The bond order of a molecule can be calculated by subtracting the number of electrons in anti-bonding orbitals from the number of bonding orbitals, and the resulting number is then divided by two. A molecule is expected to be stable if it has bond order larger than zero. It is adequate to consider the valence electron to determine the bond order. Because (for principal quantum number n > 1) when MOs are derived from 1s AOs, the difference in number of electrons in bonding and anti-bonding molecular orbital is zero. So, there is no net effect on bond order if the electron is not the valence one.
From bond order, one can predict whether a bond between two atoms will form or not. For example, the existence of He2 molecule. From the molecular orbital diagram, the bond order is . That means, no bond formation will occur between two He atoms which is seen experimentally. It can be detected under very low temperature and pressure molecular beam and has binding energy of approximately 0.001 J/mol.
Besides, the strength of a bond can also be realized from bond order (BO). For example:
For H2: Bond order is ; bond energy is 436 kJ/mol.
For H2: Bond order is ; bond energy is 171 kJ/mol.
As the bond order of H2 is smaller than H2, it should be less stable which is observed experimentally and can be seen from the bond energy.
Overview
| This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (September 2020) (Learn how and when to remove this message) |
MOT provides a global, delocalized perspective on chemical bonding. In MO theory, any electron in a molecule may be found anywhere in the molecule, since quantum conditions allow electrons to travel under the influence of an arbitrarily large number of nuclei, as long as they are in eigenstates permitted by certain quantum rules. Thus, when excited with the requisite amount of energy through high-frequency light or other means, electrons can transition to higher-energy molecular orbitals. For instance, in the simple case of a hydrogen diatomic molecule, promotion of a single electron from a bonding orbital to an antibonding orbital can occur under UV radiation. This promotion weakens the bond between the two hydrogen atoms and can lead to photodissociation, the breaking of a chemical bond due to the absorption of light.
Molecular orbital theory is used to interpret ultraviolet–visible spectroscopy (UV–VIS). Changes to the electronic structure of molecules can be seen by the absorbance of light at specific wavelengths. Assignments can be made to these signals indicated by the transition of electrons moving from one orbital at a lower energy to a higher energy orbital. The molecular orbital diagram for the final state describes the electronic nature of the molecule in an excited state.
Although in MO theory some molecular orbitals may hold electrons that are more localized between specific pairs of molecular atoms, other orbitals may hold electrons that are spread more uniformly over the molecule. Thus, overall, bonding is far more delocalized in MO theory, which makes it more applicable to resonant molecules that have equivalent non-integer bond orders than valence bond theory. This makes MO theory more useful for the description of extended systems.
Robert S. Mulliken, who actively participated in the advent of molecular orbital theory, considers each molecule to be a self-sufficient unit. He asserts in his article:
...Attempts to regard a molecule as consisting of specific atomic or ionic units held together by discrete numbers of bonding electrons or electron-pairs are considered as more or less meaningless, except as an approximation in special cases, or as a method of calculation . A molecule is here regarded as a set of nuclei, around each of which is grouped an electron configuration closely similar to that of a free atom in an external field, except that the outer parts of the electron configurations surrounding each nucleus usually belong, in part, jointly to two or more nuclei....
An example is the MO description of benzene, C
6H
6, which is an aromatic hexagonal ring of six carbon atoms and three double bonds. In this molecule, 24 of the 30 total valence bonding electrons – 24 coming from carbon atoms and 6 coming from hydrogen atoms – are located in 12 σ (sigma) bonding orbitals, which are located mostly between pairs of atoms (C–C or C–H), similarly to the electrons in the valence bond description. However, in benzene the remaining six bonding electrons are located in three π (pi) molecular bonding orbitals that are delocalized around the ring. Two of these electrons are in an MO that has equal orbital contributions from all six atoms. The other four electrons are in orbitals with vertical nodes at right angles to each other. As in the VB theory, all of these six delocalized π electrons reside in a larger space that exists above and below the ring plane. All carbon–carbon bonds in benzene are chemically equivalent. In MO theory this is a direct consequence of the fact that the three molecular π orbitals combine and evenly spread the extra six electrons over six carbon atoms.

In molecules such as methane, CH
4, the eight valence electrons are found in four MOs that are spread out over all five atoms. It is possible to transform the MOs into four localized sp orbitals. Linus Pauling, in 1931, hybridized the carbon 2s and 2p orbitals so that they pointed directly at the hydrogen 1s basis functions and featured maximal overlap. However, the delocalized MO description is more appropriate for predicting ionization energies and the positions of spectral absorption bands. When methane is ionized, a single electron is taken from the valence MOs, which can come from the s bonding or the triply degenerate p bonding levels, yielding two ionization energies. In comparison, the explanation in valence bond theory is more complicated. When one electron is removed from an sp orbital, resonance is invoked between four valence bond structures, each of which has a single one-electron bond and three two-electron bonds. Triply degenerate T2 and A1 ionized states (CH4) are produced from different linear combinations of these four structures. The difference in energy between the ionized and ground state gives the two ionization energies.
As in benzene, in substances such as beta carotene, chlorophyll, or heme, some electrons in the π orbitals are spread out in molecular orbitals over long distances in a molecule, resulting in light absorption in lower energies (the visible spectrum), which accounts for the characteristic colours of these substances. This and other spectroscopic data for molecules are well explained in MO theory, with an emphasis on electronic states associated with multicenter orbitals, including mixing of orbitals premised on principles of orbital symmetry matching. The same MO principles also naturally explain some electrical phenomena, such as high electrical conductivity in the planar direction of the hexagonal atomic sheets that exist in graphite. This results from continuous band overlap of half-filled p orbitals and explains electrical conduction. MO theory recognizes that some electrons in the graphite atomic sheets are completely delocalized over arbitrary distances, and reside in very large molecular orbitals that cover an entire graphite sheet, and some electrons are thus as free to move and therefore conduct electricity in the sheet plane, as if they resided in a metal.
See also
- Cis effect
- Configuration interaction
- Coupled cluster
- Frontier molecular orbital theory
- Ligand field theory (MO theory for transition metal complexes)
- Møller–Plesset perturbation theory
- Quantum chemistry computer programs
- Semi-empirical quantum chemistry methods
- Valence bond theory
References
- Daintith, J. (2004). Oxford Dictionary of Chemistry. New York: Oxford University Press. ISBN 978-0-19-860918-6.
- Licker, Mark, J. (2004). McGraw-Hill Concise Encyclopedia of Chemistry. New York: McGraw-Hill. ISBN 978-0-07-143953-4.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Miessler, Gary L.; Fischer, Paul J.; Tarr, Donald A. (2013-04-08). Inorganic Chemistry. Pearson Education. ISBN 978-0-321-91779-9.
- Coulson, Charles, A. (1952). Valence. Oxford at the Clarendon Press.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Mulliken, Robert S. (1972) . "Spectroscopy, Molecular Orbitals, and Chemical Bonding" (PDF) (Press release). Nobel Lectures, Chemistry 1963–1970. Amsterdam: Elsevier Publishing Company.
- Hückel, Erich (1934). "Theory of free radicals of organic chemistry". Trans. Faraday Soc. 30: 40–52. doi:10.1039/TF9343000040.
- Lennard-Jones, J.E. (1929). "The electronic structure of some diatomic molecules". Trans. Faraday Soc. 25: 668–686. Bibcode:1929FaTr...25..668L. doi:10.1039/TF9292500668.
- Coulson, C.A. Valence (2nd ed., Oxford University Press 1961), p.103
- Pauling, Linus (1931). "The Nature of the Chemical Bond. II. The One-Electron Bond and the Three-Electron Bond". J. Am. Chem. Soc. 53 (9): 3225–3237. doi:10.1021/ja01360a004.
- Hall, George G. (1991). "The Lennard-Jones paper of 1929 and the foundations of Molecular Orbital Theory". Advances in Quantum Chemistry. 22: 1–6. Bibcode:1991AdQC...22....1H. doi:10.1016/S0065-3276(08)60361-5. ISBN 978-0-12-034822-0. ISSN 0065-3276.
- E. Hückel, Zeitschrift für Physik, 70, 204 (1931); 72, 310 (1931); 76, 628 (1932); 83, 632 (1933).
- Hückel Theory for Organic Chemists, C. A. Coulson, B. O'Leary and R. B. Mallion, Academic Press, 1978.
- Coulson, C.A. (1938), "Self-consistent field for molecular hydrogen", Mathematical Proceedings of the Cambridge Philosophical Society, 34 (2): 204–212, Bibcode:1938PCPS...34..204C, doi:10.1017/S0305004100020089, S2CID 95772081
- Hall, G.G. (7 August 1950). "The Molecular Orbital Theory of Chemical Valency. VI. Properties of Equivalent Orbitals". Proc. R. Soc. A. 202 (1070): 336–344. Bibcode:1950RSPSA.202..336H. doi:10.1098/rspa.1950.0104. S2CID 123260646.
- ^ Jensen, Frank (1999). Introduction to Computational Chemistry. John Wiley and Sons. ISBN 978-0-471-98425-2.
- ^ Miessler and Tarr (2013), Inorganic Chemistry, 5th ed, 117-165, 475-534.
- Miessler, Gary L.; Fischer, Paul J.; Tarr, Donald A. (2013-04-08). Inorganic Chemistry. Pearson Education. ISBN 978-0-321-91779-9.
- Mulliken, R. S. (October 1955). "Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I". The Journal of Chemical Physics. 23 (10): 1833–1840. Bibcode:1955JChPh..23.1833M. doi:10.1063/1.1740588. ISSN 0021-9606.
- Griffith, J.S. and L.E. Orgel. "Ligand Field Theory". Q. Rev. Chem. Soc. 1957, 11, 381-383
External links
- Molecular Orbital Theory - Purdue University
- Molecular Orbital Theory - Sparknotes
- Molecular Orbital Theory - Mark Bishop's Chemistry Site
- Introduction to MO Theory - Queen Mary, London University
- Molecular Orbital Theory - a related terms table
- An introduction to Molecular Group Theory - Oxford University
| Chemical bonding theory | |||||||
|---|---|---|---|---|---|---|---|
| Types of bonds |
| ||||||
| Valence bond theory |
| ||||||
| Molecular orbital theory |
| ||||||


 . That means, no bond formation will occur between two He atoms which is seen experimentally. It can be detected under very low temperature and pressure molecular beam and has
. That means, no bond formation will occur between two He atoms which is seen experimentally. It can be detected under very low temperature and pressure molecular beam and has  ; bond energy is 436 kJ/mol.
; bond energy is 436 kJ/mol.
 ; bond energy is 171 kJ/mol.
; bond energy is 171 kJ/mol.