| Revision as of 22:12, 26 September 2008 editSmackBot (talk | contribs)3,734,324 editsm Embolden title and general fixes, added uncategorised tag← Previous edit | Latest revision as of 13:24, 13 October 2023 edit undoSkynxnex (talk | contribs)Extended confirmed users, New page reviewers, Pending changes reviewers, Rollbackers26,027 edits Undid revision 1179895041 by 2601:642:4600:3F80:7C5B:ED3B:67BE:2F38 (talk): even if it's functionally the same as the natural logarithm, it is independently discussed in sources to likely merit an articleTags: Removed redirect Undo | ||
| (53 intermediate revisions by 33 users not shown) | |||
| Line 1: | Line 1: | ||
| ⚫ | ] | ||
| ⚫ | |||
| ]'']] | |||
| The term '''Napierian logarithm''' or '''Naperian logarithm''', named after ], is often used to mean the ]. Napier did not introduce this ''natural'' logarithmic function, although it is named after him.<ref>{{cite book |last1=Larson |first1=Ron |last2=Hostetler |first2=Robert P. |last3=Edwards |first3=Bruce H. |year=2008 |title=Essential Calculus Early Transcendental Functions |publisher=Richard Stratton |isbn=978-0-618-87918-2 |location=U.S.A |pages=119}}</ref><ref name=Hobson>{{Citation|author=Ernest William Hobson|title=John Napier and the Invention of Logarithms, 1614|year=1914|publisher=The University Press|location=Cambridge|url=https://jscholarship.library.jhu.edu/bitstream/handle/1774.2/34187/31151005337641.pdf}}</ref> | |||
| ⚫ | However, if it is taken to mean the "]s" as originally produced by Napier, it is a function given by (in terms of the modern ]): | ||
| ⚫ | : <math>\mathrm{NapLog}(x) = -10^7 \ln (x/10^7) </math> | ||
| The Napierian logarithm satisfies identities quite similar to the modern logarithm, such as<ref>{{cite web|last1=Roegel|first1=Denis|title=Napier's ideal construction of the logarithms|url=https://hal.inria.fr/inria-00543934/document|website=HAL|publisher=INRIA|accessdate=7 May 2018}}</ref> | |||
| ⚫ | ] | ||
| : <math>\mathrm{NapLog}(xy) \approx \mathrm{NapLog}(x)+\mathrm{NapLog}(y)-161180956</math> | |||
| or | |||
| ⚫ | :<math>\mathrm{NapLog}(xy/10^7) = \mathrm{NapLog}(x)+\mathrm{NapLog}(y) </math> | ||
| In Napier's 1614 '']'', he provides tables of logarithms of sines for 0 to 90°, where the values given (columns 3 and 5) are | |||
| ⚫ | <math>\mathrm{NapLog}( |
||
| : <math>\mathrm{NapLog}(\theta) = -10^7 \ln (\sin(\theta)) </math> | |||
| (Being a quotient of logarithms, the base of the logarithm chosen is irrelevant.) | |||
| == Properties == | |||
| It is not a logarithm to any particular base in the modern sense of the term, however, it can be rewritten as: | |||
| Napier's "logarithm" is related to the ] by the relation | |||
| <math>\mathrm{NapLog}(x) = \log_{\frac{10^7}{10^7 - 1}} 10^7 - \log_{\frac{10^7}{10^7 - 1}} x</math> | |||
| : <math>\mathrm{NapLog} (x) \approx 10000000 (16.11809565 - \ln x)</math> | |||
| and hence it is a linear function of a particular logarithm, and so satisfies identities quite similar to the modern one. | |||
| and to the ] by | |||
| <math>\mathrm{NapLog} (x) \approx |
: <math>\mathrm{NapLog} (x) \approx 23025851 (7 - \log_{10} x).</math> | ||
| Note that | |||
| and to the ] by | |||
| : <math>16.11809565 \approx 7 \ln \left(10\right) </math> | |||
| and | |||
| : <math>23025851 \approx 10^7 \ln (10).</math> | |||
| Napierian logarithms are essentially natural logarithms with decimal points shifted 7 places rightward and with sign reversed. For instance the logarithmic values | |||
| :<math>\ln(.5000000) = -0.6931471806</math> | |||
| :<math>\ln(.3333333) = -1.0986123887</math> | |||
| would have the corresponding Napierian logarithms: | |||
| :<math>\mathrm{NapLog}(5000000) = 6931472</math> | |||
| :<math>\mathrm{NapLog}(3333333) = 10986124</math> | |||
| For further detail, see ]. | |||
| ==References== | |||
| ⚫ | <math>\mathrm{NapLog} |
||
| {{Reflist}} | |||
| *{{citation | |||
| | last1 = Boyer | |||
| | first1 = Carl B. | |||
| | last2 = Merzbach | |||
| | first2 = Uta C. | |||
| | author2-link = Uta Merzbach | |||
| | isbn = 978-0-471-54397-8 | |||
| | page = | |||
| | publisher = Wiley | |||
| | title = A History of Mathematics | |||
| | year = 1991 | |||
| | url-access = registration | |||
| | url = https://archive.org/details/historyofmathema00boye/page/313 | |||
| }}. | |||
| *{{cite book|author=C.H.Jr. Edwards|title=The Historical Development of the Calculus|url=https://books.google.com/books?id=ilrlBwAAQBAJ&q=napier+logarithm|date=6 December 2012|publisher=Springer Science & Business Media|isbn=978-1-4612-6230-5}}. | |||
| *{{citation | |||
| | last = Phillips | |||
| | first = George McArtney | |||
| | isbn = 978-0-387-95022-8 | |||
| | page = | |||
| | publisher = Springer-Verlag | |||
| | series = CMS Books in Mathematics | |||
| | title = Two Millennia of Mathematics: from Archimedes to Gauss | |||
| | volume = 6 | |||
| | year = 2000 | |||
| | url = https://archive.org/details/twomillenniaofma0000phil/page/61 | |||
| }}. | |||
| ==External links== | |||
| {{Uncategorizedstub|date=September 2008}} | |||
| * Denis Roegel (2012) , from the Loria Collection of Mathematical Tables. | |||
| ] | |||
| {{math-stub}} | |||
Latest revision as of 13:24, 13 October 2023
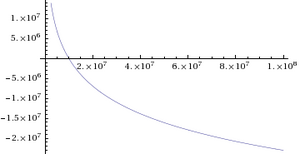

The term Napierian logarithm or Naperian logarithm, named after John Napier, is often used to mean the natural logarithm. Napier did not introduce this natural logarithmic function, although it is named after him. However, if it is taken to mean the "logarithms" as originally produced by Napier, it is a function given by (in terms of the modern natural logarithm):
The Napierian logarithm satisfies identities quite similar to the modern logarithm, such as
or
In Napier's 1614 Mirifici Logarithmorum Canonis Descriptio, he provides tables of logarithms of sines for 0 to 90°, where the values given (columns 3 and 5) are
Properties
Napier's "logarithm" is related to the natural logarithm by the relation
and to the common logarithm by
Note that
and
Napierian logarithms are essentially natural logarithms with decimal points shifted 7 places rightward and with sign reversed. For instance the logarithmic values
would have the corresponding Napierian logarithms:
For further detail, see history of logarithms.
References
- Larson, Ron; Hostetler, Robert P.; Edwards, Bruce H. (2008). Essential Calculus Early Transcendental Functions. U.S.A: Richard Stratton. p. 119. ISBN 978-0-618-87918-2.
- Ernest William Hobson (1914), John Napier and the Invention of Logarithms, 1614 (PDF), Cambridge: The University Press
- Roegel, Denis. "Napier's ideal construction of the logarithms". HAL. INRIA. Retrieved 7 May 2018.
- Boyer, Carl B.; Merzbach, Uta C. (1991), A History of Mathematics, Wiley, p. 313, ISBN 978-0-471-54397-8.
- C.H.Jr. Edwards (6 December 2012). The Historical Development of the Calculus. Springer Science & Business Media. ISBN 978-1-4612-6230-5..
- Phillips, George McArtney (2000), Two Millennia of Mathematics: from Archimedes to Gauss, CMS Books in Mathematics, vol. 6, Springer-Verlag, p. 61, ISBN 978-0-387-95022-8.
External links
- Denis Roegel (2012) Napier’s Ideal Construction of the Logarithms, from the Loria Collection of Mathematical Tables.











