| Revision as of 11:15, 9 June 2009 editOptisop (talk | contribs)2 edits →Cutting stock problem in paper, film and metal industries← Previous edit | Latest revision as of 17:31, 21 October 2024 edit undoCoconutOctopus (talk | contribs)Extended confirmed users, Page movers, IP block exemptions, New page reviewers, Pending changes reviewers, Rollbackers6,485 edits Reverted good faith edits by 212.15.149.185 (talk)Tags: Twinkle Undo | ||
| (158 intermediate revisions by 81 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Mathematical problem in operations research}} | |||
| The '''cutting stock problem''' is an ] problem, or more specifically, an ] problem. It arises from many applications in industry. Imagine that you work in a paper mill and you have a number of rolls of paper of fixed width waiting to be cut, yet different customers want different numbers of rolls of various-sized widths. How are you going to cut the rolls so that you minimize the waste (amount of left-overs)? | |||
| {{more citations needed|date=April 2015}} | |||
| In ], the '''cutting-stock problem''' is the problem of cutting standard-sized pieces of ] material, such as paper rolls or ], into pieces of specified sizes while minimizing material wasted. It is an ] in ] that arises from applications in industry. In terms of ], the problem is an ] problem reducible to the ]. The problem can be formulated as an ] problem. | |||
| == Illustration of one-dimensional cutting-stock problem == | |||
| Solving this problem to optimality can be economically significant: a difference of 1% for a modern paper machine can be worth more than one million USD per year. | |||
| A paper machine can produce an unlimited number of master (jumbo) rolls, each 5600 mm wide. The following 13 items must be cut, in the table below. | |||
| == Formulation and solution approaches == | |||
| The standard formulation for the cutting stock problem (but not the only one) starts with a list of <math>m</math> orders, each requiring <math>q_j</math>, ''j'' = 1,...,''m'' pieces. We then construct a list of all possible combinations of cuts (often called "patterns"), associating with each pattern a positive integer variable <math>x_i</math> representing how many times each pattern is to be used. The linear integer program is then: | |||
| The important thing about this kind of problem is that many different product units can be made from the same master roll, and the number of possible combinations is itself very large, in general, and not trivial to enumerate. | |||
| :minimize <math>\sum_{i=1}^n c_i x_i</math> | |||
| The problem therefore is to find an optimum set of patterns of making product rolls from the master roll, such that the demand is satisfied and waste is minimized. | |||
| :subject to <math>\sum_{i=1}^n a_{ij} x_i \ge q_j, \quad \quad \forall j=1,\dots,m</math> and | |||
| ::{| class="wikitable" | |||
| :<math>x_i \ge 0</math>, integer | |||
| |- | |||
| ! width="80pt" | Width | |||
| ! width="80pt" | #Items | |||
| |- | |||
| | align=center | 1380 || align=center | 22 | |||
| |- | |||
| | align=center | 1520 || align=center | 25 | |||
| |- | |||
| | align=center | 1560 || align=center | 12 | |||
| |- | |||
| | align=center | 1710 || align=center | 14 | |||
| |- | |||
| | align=center | 1820 || align=center | 18 | |||
| |- | |||
| | align=center | 1880 || align=center | 18 | |||
| |- | |||
| | align=center | 1930 || align=center | 20 | |||
| |- | |||
| | align=center | 2000 || align=center | 10 | |||
| |- | |||
| | align=center | 2050 || align=center | 12 | |||
| |- | |||
| | align=center | 2100 || align=center | 14 | |||
| |- | |||
| | align=center | 2140 || align=center | 16 | |||
| |- | |||
| | align=center | 2150 || align=center | 18 | |||
| |- | |||
| | align=center | 2200 || align=center | 20 | |||
| |} | |||
| ===Bounds and checks=== | |||
| where <math>a_{ij}</math> is the number of times order <math>j</math> appears in pattern <math>i</math> and <math>c_i</math> is the cost (often the waste) of pattern <math>i</math>. The precise nature of the quantity constraints can lead to subtly different mathematical characteristics. The above formulation's quantity constraints are '''minimum''' constraints (at least the given amount of each order must be produced, but possibly more). When <math>c_i=1</math> the objective minimises the number of utilised master items. The most general formulation has two-sided constraints (and in this case a minimum-waste solution may consume more than the minimum number of master items): | |||
| A simple lower bound is obtained by dividing the total amount of product by the size of each master roll. The total product required is 1380 x 22 + 1520 x 25 + ... + 2200 x 20 = 407160 mm. Each master roll is 5600 mm, requiring a minimum of 72.7 rolls, which means 73 rolls or more are required. | |||
| :<math>q_j \le \sum_{i=1}^n a_{ij} x_i \le Q_j, \quad \quad \forall j=1,\dots,m</math> | |||
| This formulation applies not just to one-dimensional problems. Many variations are possible, including one where the objective is not to minimise the waste, but to maximise the total value of the produced items, allowing each order to have a different value. | |||
| In general, the number of possible patterns grows exponentially as a function of ''m'', the number of orders. As the number of orders increases, it may therefore become impractical to enumerate the possible cutting patterns. | |||
| An alternative is to use a ] approach. This method solves the cutting stock problem by starting with just a few patterns. It generates additional patterns when they are needed. For the one-dimensional case, the new patterns are introduced by solving an auxiliary optimization problem called the ], using dual variable information from the ]. The knapsack problem has well-known methods to solve it, such as ] and ]. The Delayed Column Generation method can be much more efficient than the original approach, particularly as the size of the problem grows. The column generation approach was pioneered by Gilmore and Gomory in a series of papers published in the 1960's.<ref name=Gilmore61>Gilmore P. C., R. E. Gomory (1961). ''A linear programming approach to the cutting-stock problem''. Operations Research 9: 849-859</ref> <ref name=Gilmore63>Gilmore P. C., R. E. Gomory (1963). ''A linear programming approach to the cutting-stock problem - Part II''. Operations Research 11: 863-888</ref>. Gilmore and Gomory showed that this approach is guaranteed to converge to the (fractional) optimal solution, without needing to enumerate all the possible patterns in advance. | |||
| A limitation of the original Gilmore and Gomory method is that it does not handle integrality, so the solution may contain fractions, e.g. a particular pattern should be produced 3.67 times. Rounding to the nearest integer often does not work, in the sense that it may lead to a sub-optimal solution and/or under- or over-production of some of the orders (and possible infeasibility in the presence of two-sided demand constraints). This limitation is overcome in modern algorithms, which can solve to optimality (in the sense of finding solutions with minimum waste) very large instances of the problem (generally larger than encountered in practice<ref name=Goulimis1990>Goulimis C (1990). ''Optimal solutions for the cutting stock problem''. European Journal of Operational Research 44: 197-208</ref> <ref name=Carvalho1998>de Carvalho V (1998). ''Exact solution of cutting stock problems using column generation and branch-and-bound''. International Transactions in Operational Research 5: 35–44</ref>). | |||
| The cutting stock problem is often highly degenerate, in that multiple solutions with the same waste are possible. This degeneracy arises because it is possible to move items around, creating new patterns, without affecting the waste. This give arise to a whole collection of related problems which are concerned with some other criterion, such as the following: | |||
| * The minimum pattern count problem: to find a minimum-pattern-count solution amongst the minimum-waste solutions. This is a very hard problem, even when the waste is known<ref name=Umetani2003>S. Umetani, M. Yagiura, and T. Ibaraki (2003). ''One dimensional cutting stock problem to minimize the number of different patterns''. European Journal of Operational Research 146, 388–402</ref><ref name=Diegel1996>A. Diegel, E. Montocchio, E. Walters, S. van Schalkwyk and S. Naidoo (1996). ''Setup minimizing conditions in the trim loss problem''. European Journal of Operational Research 95:631-640</ref>. There is a ] that any equality-constrained one-dimensional instance with ''n'' orders has at least one minimum waste solution with no more than ''n'' + 1 patterns. No upper bound to the number of patterns is known either, examples with ''n'' + 5 are known. | |||
| * The minimum stack problem: this is concerned with the sequencing of the patterns so as not to have too many partially completed orders at any time. This was an open problem until 2007, when an efficient algorithm based on dynamic programming was published<ref name=Banda2007> Maria Garcia de la Banda, P. J. Stuckey. ''Dynamic Programming to Minimize the Maximum Number of Open Stacks''. INFORMS Journal on Computing, Vol. 19, No. 4, Fall 2007, 607-617.</ref>. | |||
| * The minimum number of knife changes problem (for the one-dimensional problem): this is concerned with sequencing and permuting the patterns so as to minimise the number of times the slitting knives have to be moved. This is a special case of the generalised ]. | |||
| == Illustration of one-dimensional stock cutting problem == | |||
| A paper machine can produce an unlimited number of master (jumbo) rolls, each 5600 mm wide. The following 13 items must be cut: | |||
| ::{| class="wikitable" | |||
| |- | |||
| ! width="80pt" | Width | |||
| ! width="80pt" | Rolls | |||
| |- | |||
| | align=center | 1380 || align=center | 22 | |||
| |- | |||
| | align=center | 1520 || align=center | 25 | |||
| |- | |||
| | align=center | 1560 || align=center | 12 | |||
| |- | |||
| | align=center | 1710 || align=center | 14 | |||
| |- | |||
| | align=center | 1820 || align=center | 18 | |||
| |- | |||
| | align=center | 1880 || align=center | 18 | |||
| |- | |||
| | align=center | 1930 || align=center | 20 | |||
| |- | |||
| | align=center | 2000 || align=center | 10 | |||
| |- | |||
| | align=center | 2050 || align=center | 12 | |||
| |- | |||
| | align=center | 2100 || align=center | 14 | |||
| |- | |||
| | align=center | 2140 || align=center | 16 | |||
| |- | |||
| | align=center | 2150 || align=center | 18 | |||
| |- | |||
| | align=center | 2200 || align=center | 20 | |||
| |} | |||
| ===Solution=== | ===Solution=== | ||
| ] | ] | ||
| There are 308 possible patterns for this small instance. The optimal answer requires 73 master rolls and has 0.401% waste; it |
There are 308 possible patterns for this small instance. The optimal answer requires 73 master rolls and has 0.401% waste; it can be shown computationally that in this case the minimum number of patterns with this level of waste is 10. It can also be computed that 19 different such solutions exist, each with 10 patterns and a waste of 0.401%, of which one such solution is shown below and in the picture: | ||
| :{| class="wikitable |
:{| class="wikitable" | ||
| !Repetition | !Repetition | ||
| !align=center | Contents | !align=center | Contents | ||
| Line 93: | Line 73: | ||
| | style="border-bottom:3px solid grey" align=center | 2 || 1710 + 1710 + 2150 | | style="border-bottom:3px solid grey" align=center | 2 || 1710 + 1710 + 2150 | ||
| |- | |- | ||
| | align=center | '''73''' |
| align=center | '''73''' | ||
| |} | |} | ||
| == Classification == | == Classification == | ||
| Cutting |
Cutting-stock problems can be classified in several ways.<ref name="Wäscher2007">Wäscher, G.; Haußner, H.; Schumann, H. '' {{Webarchive|url=https://web.archive.org/web/20200424185417/https://prolog.univie.ac.at/teaching/LVAs/KFK-Seminar/SS15/2007%20W%E4scherHaussnerSchuhmann%20An%20improved%20typology%20of%20cutting%20and%20packing%20problems.pdf |date=2020-04-24 }}''. European Journal of Operational Research Volume 183, Issue 3, 1109-1130</ref> One way is the dimensionality of the cutting: the above example illustrates a one-dimensional (1D) problem; other industrial applications of 1D occur when cutting pipes, cables, and steel bars. Two-dimensional (2D) problems are encountered in furniture, clothing and glass production. When either the master item or the required parts are irregular-shaped (a situation often encountered in the leather, textile, metals industries) this is referred to as the ''nesting'' problem. | ||
| Not many three-dimensional (3D) applications involving cutting are known; however the closely related 3D ] has many industrial applications, such as packing objects into ]s (see e.g. ]: the related ] problem has been studied since the 17th century (])). | |||
| ==Cutting stock problem in paper, film and metal industries== | |||
| Industrial applications of the cutting stock problems for high production volumes arise especially when basic material is produced in large rolls that are further cut into smaller units. This is done e.g. in paper and plastic film industries but also in production of flat metals like steel or brass. There are many variants and additional constraints arising form special production constraints due to machinery and process limits, customer requirements and quality issues; some examples are: | |||
| * Two-stage, where the rolls produced in the first stage are then processed a second time. For instance, all office stationery (e.g. ] size in Europe, ] in US) is produced in such a process. The complication arises because the machinery in the second stage is narrower than the primary. Efficient utilisation of both stages of production is important (from an energy or material use perspective) and what is efficient for the primary stage may be inefficient for the secondary, leading to trade-offs. ] (used in packaging of snacks), and plastic extrusion on paper (used in ], e.g. juice cartons) are further examples of such a process. | |||
| ==Applications== | |||
| Industrial applications of cutting-stock problems for high production volumes arise especially when basic material is produced in large rolls that are further cut into smaller units (see ]). This is done e.g. in paper and plastic film industries but also in production of flat metals like steel or brass. There are many variants and additional constraints arising from special production constraints due to machinery and process limits, customer requirements and quality issues; some examples are: | |||
| * Two-stage, where the rolls produced in the first stage are then processed a second time. For instance, all office stationery (e.g. ] size in Europe, ] in US) is produced in such a process. The complication arises because the machinery in the second stage is narrower than the primary. Efficient utilisation of both stages of production is important (from an energy or material use perspective) and what is efficient for the primary stage may be inefficient for the secondary, leading to trade-offs. ] (used in packaging of snacks), and plastic extrusion on paper (used in ], e.g. juice cartons) are further examples of such a process. | |||
| * Winder constraints where the slitting process has physical or logical constraints: a very common constraint is that only a certain number of slitting knives are available, so that feasible patterns should not contain more than a maximum number of rolls. Because winder machinery is not standardised, very many other constraints are encountered. | * Winder constraints where the slitting process has physical or logical constraints: a very common constraint is that only a certain number of slitting knives are available, so that feasible patterns should not contain more than a maximum number of rolls. Because winder machinery is not standardised, very many other constraints are encountered. | ||
| * An example of a customer requirement is when a particular order cannot be satisfied from either of the two edge positions: this is because the edges of the sheet tend to have greater variations in thickness and some applications can be very sensitive to these. | * An example of a customer requirement is when a particular order cannot be satisfied from either of the two edge positions: this is because the edges of the sheet tend to have greater variations in thickness and some applications can be very sensitive to these. | ||
| * An example of a quality issue is when the master roll contains defects that have to be cut around. Expensive materials with demanding quality characteristics such as ] or ] have to be carefully optimised so that the wasted area is minimised. | * An example of a quality issue is when the master roll contains defects that have to be cut around. Expensive materials with demanding quality characteristics such as ] or ] have to be carefully optimised so that the wasted area is minimised. | ||
| * Multi-machine problems arise when orders can be produced on more than one machine and these machines have different widths. Generally availability of more than one master roll width improves the waste considerably; in practice however additional order splitting constraints may have to be taken into account. | * Multi-machine problems arise when orders can be produced on more than one machine and these machines have different widths. Generally availability of more than one master roll width improves the waste considerably; in practice however additional order splitting constraints may have to be taken into account. | ||
| * There is also a semi-continuous problem, where the produced rolls do not have to be of the same diameter, but can vary within a range. This typically occurs with sheet orders. This is sometimes known as a ''1½ dimensional'' problem. This variant also occurs in the production of ], where it is called, somewhat confusingly, the ''corrugator scheduling problem''. | |||
| * Because some paper machines are relatively narrow compared to the demanded items, some companies have invested in a ''skiving'' (also known as a ''web-welding'') secondary process, whereby two reels (produced by slitting the initial jumbo reels) are joined side-by-side (with a little overlap) to make up a wider roll. Producing narrower reels in the primary process leads to lower overall waste.<ref name=Johnson1997>M.P. Johnson, C. Rennick & E. Zak (1997), '''', SIAM Review, 472-483</ref> | |||
| * In the metals industry one key difference is that typically the master rolls are produced earlier and are generally different from each other (both in terms of width and length). Therefore, there are similarities with the multi-machine problem mentioned above. The presence of length variations creates a 2-D problem, because waste can occur both width-wise and length-wise.{{citation needed|date=February 2016}} | |||
| * The ] is another 2-D problem of cutting sheets into rectangles of specified sizes, however only cuts that continue all the way across each sheet are allowed. Industrial applications of this problem can be found in the glass industry. | |||
| ] | |||
| ] | |||
| * The cutting stock problem of determining, for the one-dimensional case, the best master size that will meet given demand is known as the ''assortment'' problem.<ref>{{Cite journal | doi = 10.1111/j.1475-3995.2009.00724.x| title = The generalized assortment and best cutting stock length problems| journal = International Transactions in Operational Research| volume = 17| pages = 35–49| year = 2010| last1 = Raffensperger | first1 = J. F. }}</ref> | |||
| == History == | |||
| The cutting stock problem was first formulated by ] in 1939.<ref>L. V. Kantorovich ''''. Leningrad State University. 1939</ref> In 1951 before computers became widely available, L. V. ] and V. A. ] suggested<ref>{{cite book | |||
| | author = Kantorovich L. V. and Zalgaller V. A. . | |||
| | title = Calculation of Rational Cutting of Stock | |||
| | publisher = Lenizdat, Leningrad | |||
| | year = 1951 | |||
| }}</ref> solving the problem of the economical use of material at the cutting stage with the help of linear programming. The proposed technique was later called the ''column generation method''. | |||
| == Mathematical formulation and solution approaches == | |||
| The standard formulation for the cutting-stock problem (but not the only one) starts with a list of ''m'' orders, each requiring <math>q_j</math> pieces, where <math>j = 1,\ldots,m</math>. We then construct a list of all possible combinations of cuts (often called "patterns" or "configurations"). Let <math>C</math> be the number of those patterns. We associate with each pattern a positive integer variable <math>x_i</math>, representing how many times pattern <math>i</math> is to be used, where <math>i = 1,\ldots,C</math>. The linear integer program is then: | |||
| :<math>\min\sum_{i=1}^C c_i x_i</math> | |||
| :<math>\text{s.t.}\sum_{i=1}^C a_{ij} x_i \ge q_j, \quad \quad \forall j=1,\dots,m</math> | |||
| :<math>x_i \ge 0</math>, integer | |||
| where <math>a_{ij}</math> is the number of times order <math>j</math> appears in pattern <math>i</math> and <math>c_i</math> is the cost (often the waste) of pattern <math>i</math>. The precise nature of the quantity constraints can lead to subtly different mathematical characteristics. The above formulation's quantity constraints are '''minimum''' constraints (at least the given amount of each order must be produced, but possibly more). | |||
| When <math>c_i=1</math>, the objective minimises the number of utilised master items and, if the constraint for the quantity to be produced is replaced by equality, it is called the ''']'''. | |||
| The most general formulation has two-sided constraints (and in this case a minimum-waste solution may consume more than the minimum number of master items): | |||
| :<math>q_j \le \sum_{i=1}^n a_{ij} x_i \le Q_j, \quad \quad \forall j=1,\dots,m</math> | |||
| This formulation applies not just to one-dimensional problems. Many variations are possible, including one where the objective is not to minimise the waste, but to maximise the total value of the produced items, allowing each order to have a different value. | |||
| In general, the number of possible patterns grows exponentially as a function of ''m'', the number of orders. As the number of orders increases, it may therefore become impractical to enumerate the possible cutting patterns. | |||
| An alternative approach uses ]. This method solves the cutting-stock problem by starting with just a few patterns. It generates additional patterns when they are needed. For the one-dimensional case, the new patterns are introduced by solving an auxiliary optimization problem called the ], using dual variable information from the ]. The knapsack problem has well-known methods to solve it, such as ] and ]. The Delayed Column Generation method can be much more efficient than the original approach, particularly as the size of the problem grows. The ] approach as applied to the cutting stock problem was pioneered by Gilmore and Gomory in a series of papers published in the 1960s.<ref name=Gilmore61>Gilmore P. C., R. E. Gomory (1961). ''''. Operations Research 9: 849-859</ref><ref name=Gilmore63>Gilmore P. C., R. E. Gomory (1963). ''''. Operations Research 11: 863-888</ref> Gilmore and Gomory showed that this approach is guaranteed to converge to the (fractional) optimal solution, without needing to enumerate all the possible patterns in advance. | |||
| A limitation of the original Gilmore and Gomory method is that it does not handle integrality, so the solution may contain fractions, e.g. a particular pattern should be produced 3.67 times. Rounding to the nearest integer often does not work, in the sense that it may lead to a sub-optimal solution and/or under- or over-production of some of the orders (and possible infeasibility in the presence of two-sided demand constraints). This limitation is overcome in modern algorithms, which can solve to optimality (in the sense of finding solutions with minimum waste) very large instances of the problem (generally larger than encountered in practice<ref name=Goulimis1990>Goulimis C (1990). ''''. European Journal of Operational Research 44: 197-208</ref><ref name=Carvalho1998>de Carvalho V (1998). ''''. International Transactions in Operational Research 5: 35–44</ref>). | |||
| The cutting-stock problem is often highly degenerate, in that multiple solutions with the same amount of waste are possible. This degeneracy arises because it is possible to move items around, creating new patterns, without affecting the amount of waste. This gives rise to a whole collection of related problems which are concerned with some other criterion, such as the following: | |||
| * The minimum pattern count problem: to find a minimum-pattern-count solution amongst the minimum-waste solutions. This is a very hard problem, even when the waste is known.<ref name=Umetani2003>S. Umetani, M. Yagiura, and ] (2003). ''''. European Journal of Operational Research 146, 388–402</ref><ref name=Diegel1996>A. Diegel, E. Montocchio, E. Walters, S. van Schalkwyk and S. Naidoo (1996). ''''. European Journal of Operational Research 95:631-640</ref><ref name=McDiarmid1999>C. McDiarmid (1999). ''''. Discrete Applied Mathematics, 121-130</ref> There is a ] that any equality-constrained one-dimensional instance with ''n'' sizes has at least one minimum waste solution with no more than ''n'' + 1 patterns. This conjecture was first refuted in April 2020 with an example with 9 sizes that requires 11 patterns.<ref name=Goulimis2020>Constantine Goulimis. ''''. arXiv:2004.01937</ref> | |||
| * The minimum stack problem: this is concerned with the sequencing of the patterns so as not to have too many partially completed orders at any time. This was an open problem until 2007, when an efficient algorithm based on dynamic programming was published.<ref name=Banda2007>], P. J. Stuckey. ''''. INFORMS Journal on Computing, Vol. 19, No. 4, Fall 2007, 607-617.</ref> | |||
| * The minimum number of knife changes problem (for the one-dimensional problem): this is concerned with sequencing and permuting the patterns so as to minimise the number of times the slitting knives have to be moved. This is a special case of the generalised ]. | |||
| == See also == | |||
| * ] | |||
| * There is also a semi-continuous problem, where the produced rolls do not have to be of the same diameter, but can vary within a range. This typically occurs with sheet orders. This is sometimes known as a ''1½ dimensional'' problem. | |||
| *] | |||
| Suppliers of such software to the paper industry include ], ], ], and ]. | |||
| == References == | == References == | ||
| {{ |
{{Reflist}} | ||
| == Further reading == | == Further reading == | ||
| *{{cite book | * {{cite book | ||
| | author = Chvátal, V. | | author = Chvátal, V. | ||
| | author-link = Václav Chvátal | |||
| | title = Linear Programming | | title = Linear Programming | ||
| | publisher = W.H. Freeman | | url = https://archive.org/details/linearprogrammin00chv| url-access = registration| publisher = W.H. Freeman | ||
| | year = 1983 | | year = 1983 | ||
| | isbn = 978- |
| isbn = 978-0-7167-1587-0}} | ||
| * Hatem Ben Amor, J.M. Valério de Carvalho, ''Cutting Stock Problems'' in Column Generation, edited by Guy Desaulniers, Jacques Desrosiers, and Marius M. Solomon, Springer, 2005, XVI, ISBN |
* Hatem Ben Amor, J.M. Valério de Carvalho, ''Cutting Stock Problems'' in Column Generation, edited by Guy Desaulniers, Jacques Desrosiers, and Marius M. Solomon, Springer, 2005, XVI, {{ISBN|0-387-25485-4}} | ||
| * M. Delorme, M. Iori, S. Martello, ''Bin packing and cutting stock problems: Mathematical models and exact algorithms'', European Journal of Operational Research 2016, 255, 1–20, {{doi|10.1016/j.ejor.2016.04.030}} | |||
| == External links == | |||
| * | |||
| * A web site, provided by the ], where you can submit one-dimensional problems with up to 10 sizes can be found . | |||
| {{DEFAULTSORT:Cutting Stock Problem}} | |||
| ] | ] | ||
| ] | ] | ||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 17:31, 21 October 2024
Mathematical problem in operations research| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Cutting stock problem" – news · newspapers · books · scholar · JSTOR (April 2015) (Learn how and when to remove this message) |
In operations research, the cutting-stock problem is the problem of cutting standard-sized pieces of stock material, such as paper rolls or sheet metal, into pieces of specified sizes while minimizing material wasted. It is an optimization problem in mathematics that arises from applications in industry. In terms of computational complexity, the problem is an NP-hard problem reducible to the knapsack problem. The problem can be formulated as an integer linear programming problem.
Illustration of one-dimensional cutting-stock problem
A paper machine can produce an unlimited number of master (jumbo) rolls, each 5600 mm wide. The following 13 items must be cut, in the table below.
The important thing about this kind of problem is that many different product units can be made from the same master roll, and the number of possible combinations is itself very large, in general, and not trivial to enumerate.
The problem therefore is to find an optimum set of patterns of making product rolls from the master roll, such that the demand is satisfied and waste is minimized.
Width #Items 1380 22 1520 25 1560 12 1710 14 1820 18 1880 18 1930 20 2000 10 2050 12 2100 14 2140 16 2150 18 2200 20
Bounds and checks
A simple lower bound is obtained by dividing the total amount of product by the size of each master roll. The total product required is 1380 x 22 + 1520 x 25 + ... + 2200 x 20 = 407160 mm. Each master roll is 5600 mm, requiring a minimum of 72.7 rolls, which means 73 rolls or more are required.
Solution

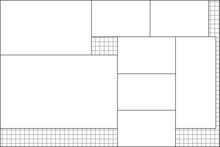
There are 308 possible patterns for this small instance. The optimal answer requires 73 master rolls and has 0.401% waste; it can be shown computationally that in this case the minimum number of patterns with this level of waste is 10. It can also be computed that 19 different such solutions exist, each with 10 patterns and a waste of 0.401%, of which one such solution is shown below and in the picture:
Repetition Contents 2 1820 + 1820 + 1820 3 1380 + 2150 + 1930 12 1380 + 2150 + 2050 7 1380 + 2100 + 2100 12 2200 + 1820 + 1560 8 2200 + 1520 + 1880 1 1520 + 1930 + 2150 16 1520 + 1930 + 2140 10 1710 + 2000 + 1880 2 1710 + 1710 + 2150 73
Classification
Cutting-stock problems can be classified in several ways. One way is the dimensionality of the cutting: the above example illustrates a one-dimensional (1D) problem; other industrial applications of 1D occur when cutting pipes, cables, and steel bars. Two-dimensional (2D) problems are encountered in furniture, clothing and glass production. When either the master item or the required parts are irregular-shaped (a situation often encountered in the leather, textile, metals industries) this is referred to as the nesting problem.
Not many three-dimensional (3D) applications involving cutting are known; however the closely related 3D packing problem has many industrial applications, such as packing objects into shipping containers (see e.g. containerization: the related sphere packing problem has been studied since the 17th century (Kepler conjecture)).
Applications
Industrial applications of cutting-stock problems for high production volumes arise especially when basic material is produced in large rolls that are further cut into smaller units (see roll slitting). This is done e.g. in paper and plastic film industries but also in production of flat metals like steel or brass. There are many variants and additional constraints arising from special production constraints due to machinery and process limits, customer requirements and quality issues; some examples are:
- Two-stage, where the rolls produced in the first stage are then processed a second time. For instance, all office stationery (e.g. A4 size in Europe, Letter size in US) is produced in such a process. The complication arises because the machinery in the second stage is narrower than the primary. Efficient utilisation of both stages of production is important (from an energy or material use perspective) and what is efficient for the primary stage may be inefficient for the secondary, leading to trade-offs. Metallised film (used in packaging of snacks), and plastic extrusion on paper (used in liquid packaging, e.g. juice cartons) are further examples of such a process.
- Winder constraints where the slitting process has physical or logical constraints: a very common constraint is that only a certain number of slitting knives are available, so that feasible patterns should not contain more than a maximum number of rolls. Because winder machinery is not standardised, very many other constraints are encountered.
- An example of a customer requirement is when a particular order cannot be satisfied from either of the two edge positions: this is because the edges of the sheet tend to have greater variations in thickness and some applications can be very sensitive to these.
- An example of a quality issue is when the master roll contains defects that have to be cut around. Expensive materials with demanding quality characteristics such as photographic paper or Tyvek have to be carefully optimised so that the wasted area is minimised.
- Multi-machine problems arise when orders can be produced on more than one machine and these machines have different widths. Generally availability of more than one master roll width improves the waste considerably; in practice however additional order splitting constraints may have to be taken into account.
- There is also a semi-continuous problem, where the produced rolls do not have to be of the same diameter, but can vary within a range. This typically occurs with sheet orders. This is sometimes known as a 1½ dimensional problem. This variant also occurs in the production of corrugated fiberboard, where it is called, somewhat confusingly, the corrugator scheduling problem.
- Because some paper machines are relatively narrow compared to the demanded items, some companies have invested in a skiving (also known as a web-welding) secondary process, whereby two reels (produced by slitting the initial jumbo reels) are joined side-by-side (with a little overlap) to make up a wider roll. Producing narrower reels in the primary process leads to lower overall waste.
- In the metals industry one key difference is that typically the master rolls are produced earlier and are generally different from each other (both in terms of width and length). Therefore, there are similarities with the multi-machine problem mentioned above. The presence of length variations creates a 2-D problem, because waste can occur both width-wise and length-wise.
- The guillotine problem is another 2-D problem of cutting sheets into rectangles of specified sizes, however only cuts that continue all the way across each sheet are allowed. Industrial applications of this problem can be found in the glass industry.

- The cutting stock problem of determining, for the one-dimensional case, the best master size that will meet given demand is known as the assortment problem.
History
The cutting stock problem was first formulated by Kantorovich in 1939. In 1951 before computers became widely available, L. V. Kantorovich and V. A. Zalgaller suggested solving the problem of the economical use of material at the cutting stage with the help of linear programming. The proposed technique was later called the column generation method.
Mathematical formulation and solution approaches
The standard formulation for the cutting-stock problem (but not the only one) starts with a list of m orders, each requiring pieces, where . We then construct a list of all possible combinations of cuts (often called "patterns" or "configurations"). Let be the number of those patterns. We associate with each pattern a positive integer variable , representing how many times pattern is to be used, where . The linear integer program is then:
- , integer
where is the number of times order appears in pattern and is the cost (often the waste) of pattern . The precise nature of the quantity constraints can lead to subtly different mathematical characteristics. The above formulation's quantity constraints are minimum constraints (at least the given amount of each order must be produced, but possibly more).
When , the objective minimises the number of utilised master items and, if the constraint for the quantity to be produced is replaced by equality, it is called the bin packing problem.
The most general formulation has two-sided constraints (and in this case a minimum-waste solution may consume more than the minimum number of master items):
This formulation applies not just to one-dimensional problems. Many variations are possible, including one where the objective is not to minimise the waste, but to maximise the total value of the produced items, allowing each order to have a different value.
In general, the number of possible patterns grows exponentially as a function of m, the number of orders. As the number of orders increases, it may therefore become impractical to enumerate the possible cutting patterns.
An alternative approach uses delayed column-generation. This method solves the cutting-stock problem by starting with just a few patterns. It generates additional patterns when they are needed. For the one-dimensional case, the new patterns are introduced by solving an auxiliary optimization problem called the knapsack problem, using dual variable information from the linear program. The knapsack problem has well-known methods to solve it, such as branch and bound and dynamic programming. The Delayed Column Generation method can be much more efficient than the original approach, particularly as the size of the problem grows. The column generation approach as applied to the cutting stock problem was pioneered by Gilmore and Gomory in a series of papers published in the 1960s. Gilmore and Gomory showed that this approach is guaranteed to converge to the (fractional) optimal solution, without needing to enumerate all the possible patterns in advance.
A limitation of the original Gilmore and Gomory method is that it does not handle integrality, so the solution may contain fractions, e.g. a particular pattern should be produced 3.67 times. Rounding to the nearest integer often does not work, in the sense that it may lead to a sub-optimal solution and/or under- or over-production of some of the orders (and possible infeasibility in the presence of two-sided demand constraints). This limitation is overcome in modern algorithms, which can solve to optimality (in the sense of finding solutions with minimum waste) very large instances of the problem (generally larger than encountered in practice).
The cutting-stock problem is often highly degenerate, in that multiple solutions with the same amount of waste are possible. This degeneracy arises because it is possible to move items around, creating new patterns, without affecting the amount of waste. This gives rise to a whole collection of related problems which are concerned with some other criterion, such as the following:
- The minimum pattern count problem: to find a minimum-pattern-count solution amongst the minimum-waste solutions. This is a very hard problem, even when the waste is known. There is a conjecture that any equality-constrained one-dimensional instance with n sizes has at least one minimum waste solution with no more than n + 1 patterns. This conjecture was first refuted in April 2020 with an example with 9 sizes that requires 11 patterns.
- The minimum stack problem: this is concerned with the sequencing of the patterns so as not to have too many partially completed orders at any time. This was an open problem until 2007, when an efficient algorithm based on dynamic programming was published.
- The minimum number of knife changes problem (for the one-dimensional problem): this is concerned with sequencing and permuting the patterns so as to minimise the number of times the slitting knives have to be moved. This is a special case of the generalised travelling salesman problem.
See also
References
- Wäscher, G.; Haußner, H.; Schumann, H. An Improved Typology of Cutting and Packing Problems Archived 2020-04-24 at the Wayback Machine. European Journal of Operational Research Volume 183, Issue 3, 1109-1130
- M.P. Johnson, C. Rennick & E. Zak (1997), Skiving addition to the cutting stock problem in the paper industry, SIAM Review, 472-483
- Raffensperger, J. F. (2010). "The generalized assortment and best cutting stock length problems". International Transactions in Operational Research. 17: 35–49. doi:10.1111/j.1475-3995.2009.00724.x.
- L. V. Kantorovich Mathematical methods of organizing and planning production. Leningrad State University. 1939
- Kantorovich L. V. and Zalgaller V. A. . (1951). Calculation of Rational Cutting of Stock. Lenizdat, Leningrad.
- Gilmore P. C., R. E. Gomory (1961). A linear programming approach to the cutting-stock problem. Operations Research 9: 849-859
- Gilmore P. C., R. E. Gomory (1963). A linear programming approach to the cutting-stock problem - Part II. Operations Research 11: 863-888
- Goulimis C (1990). Optimal solutions for the cutting stock problem. European Journal of Operational Research 44: 197-208
- de Carvalho V (1998). Exact solution of cutting stock problems using column generation and branch-and-bound. International Transactions in Operational Research 5: 35–44
- S. Umetani, M. Yagiura, and T. Ibaraki (2003). One dimensional cutting stock problem to minimize the number of different patterns. European Journal of Operational Research 146, 388–402
- A. Diegel, E. Montocchio, E. Walters, S. van Schalkwyk and S. Naidoo (1996). Setup minimizing conditions in the trim loss problem. European Journal of Operational Research 95:631-640
- C. McDiarmid (1999). Pattern Minimisation in Cutting Stock Problems. Discrete Applied Mathematics, 121-130
- Constantine Goulimis. Counterexamples in the CSP. arXiv:2004.01937
- María García de la Banda, P. J. Stuckey. Dynamic Programming to Minimize the Maximum Number of Open Stacks. INFORMS Journal on Computing, Vol. 19, No. 4, Fall 2007, 607-617.
Further reading
- Chvátal, V. (1983). Linear Programming. W.H. Freeman. ISBN 978-0-7167-1587-0.
- Hatem Ben Amor, J.M. Valério de Carvalho, Cutting Stock Problems in Column Generation, edited by Guy Desaulniers, Jacques Desrosiers, and Marius M. Solomon, Springer, 2005, XVI, ISBN 0-387-25485-4
- M. Delorme, M. Iori, S. Martello, Bin packing and cutting stock problems: Mathematical models and exact algorithms, European Journal of Operational Research 2016, 255, 1–20, doi:10.1016/j.ejor.2016.04.030
 pieces, where
pieces, where  . We then construct a list of all possible combinations of cuts (often called "patterns" or "configurations"). Let
. We then construct a list of all possible combinations of cuts (often called "patterns" or "configurations"). Let  be the number of those patterns. We associate with each pattern a positive integer variable
be the number of those patterns. We associate with each pattern a positive integer variable  , representing how many times pattern
, representing how many times pattern  is to be used, where
is to be used, where  . The linear integer program is then:
. The linear integer program is then:


 , integer
, integer is the number of times order
is the number of times order  appears in pattern
appears in pattern  is the cost (often the waste) of pattern
is the cost (often the waste) of pattern  , the objective minimises the number of utilised master items and, if the constraint for the quantity to be produced is replaced by equality, it is called the
, the objective minimises the number of utilised master items and, if the constraint for the quantity to be produced is replaced by equality, it is called the 