| Revision as of 21:06, 4 November 2009 editGiftlite (talk | contribs)Autopatrolled, Extended confirmed users, Pending changes reviewers39,612 editsm +2.← Previous edit | Latest revision as of 10:17, 24 October 2024 edit undoMonkbot (talk | contribs)Bots3,695,952 editsm Task 20: replace {lang-??} templates with {langx|??} ‹See Tfd› (Replaced 1);Tag: AWB | ||
| (71 intermediate revisions by 63 users not shown) | |||
| Line 1: | Line 1: | ||
| {{short description|Chaotic map from the torus into itself}} | |||
| In ], '''Arnold's cat map''' is a ] map from the ] into itself, named after ], who demonstrated its effects in the 1960s using an image of a ].<ref>*{{fr icon}} {{cite book|author=V. I. Arnold|coauthors=A. Avez|title=Problèmes Ergodiques de la Mécanique Classique|location=Paris|publisher=Gauthier-Villars|year=1967}}; '''English translation:''' {{cite book|author=V. I. Arnold|coauthors=A. Avez|title=Ergodic Problems in Classical Mechanics|location=New York|publisher=Benjamin|year=1968}}</ref> | |||
| ] is performed. The lines with the arrows show the direction of the contracting and expanding ]s]] | |||
| In ], '''Arnold's cat map''' is a ] map from the ] into itself, named after ], who demonstrated its effects in the 1960s using an image of a cat, hence the name.<ref name="Arnold"/> It is a simple and pedagogical example for ]s. | |||
| Thinking of the torus <math>\mathbb{T}^2</math> as <math>\mathbb{R}^2/\mathbb{Z}^2</math> Arnold's cat map is the transformation <math>\Gamma : \mathbb{T}^2 \to \mathbb{T}^2</math> given by the formula | |||
| Thinking of the torus <math>\mathbb{T}^2</math> as the ] <math>\mathbb{R}^2/\mathbb{Z}^2</math>, Arnold's cat map is the transformation <math>\Gamma : \mathbb{T}^2 \to \mathbb{T}^2</math> given by the formula | |||
| :<math>\Gamma \, : \, (x,y) \to (2x+y,x+y) \bmod 1.</math> | |||
| :<math>\Gamma (x,y) = (2x+y,x+y) \bmod 1.</math> | |||
| Equivalently, in ] notation, this is | Equivalently, in ] notation, this is | ||
| Line 9: | Line 12: | ||
| :<math>\Gamma \left( \begin{bmatrix} x \\ y \end{bmatrix} \right) = \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \bmod 1 = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \bmod 1.</math> | :<math>\Gamma \left( \begin{bmatrix} x \\ y \end{bmatrix} \right) = \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \bmod 1 = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \bmod 1.</math> | ||
| That is, with a unit |
That is, with a unit equal to the width of the square image, the image is ] one unit up, then two units to the right, and all that lies outside that unit square is shifted back by the unit until it is within the square. | ||
| ==Name== | |||
| ] is performed. The lines with the arrows show the direction of the contracting and expanding ]s]] | |||
| The map receives its name from Arnold's 1967 manuscript with André Avez, ''Problèmes ergodiques de la mécanique classique'',<ref name="Arnold"/> in which the outline of a cat was used to illustrate the action of the map on the torus. In the original book it was captioned by a humorous footnote, | |||
| ==Properties== | |||
| {{Blockquote | |||
| |text=The ] has given permission to reproduce this image, as well as others. | |||
| * Γ is ] because the matrix has ] 1 and therefore its inverse has integer entries, | |||
| }} | |||
| In Arnold's native Russian, the map is known as "] (cold soup) from a cat" ({{langx|ru|окрошка из кошки}}), in reference to the map's mixing properties, and which forms a play on words. Arnold later wrote that he found the name "Arnold's Cat" by which the map is known in English and other languages to be "strange".<ref>{{cite book |last1=Arnold |first1=V. I. |title=Lectures and Problems: A Gift to Young Mathematicians |date=2015 |publisher=Mathematical Sciences Research Institute |location=Berkeley, CA, USA}}</ref> | |||
| ==Properties== | |||
| * Γ is ] because the matrix has ] 1 and therefore its ], | |||
| * Γ is ], | * Γ is ], | ||
| * Γ has a unique ] (the ] of the square). The linear transformation which defines the map is hyperbolic: its ]s are irrational numbers, one greater and the other smaller than 1 (in absolute value), so they are associated respectively to an expanding and a contracting ] which are also the ]. The eigenspaces are orthogonal because the matrix is ]. Since the eigenvectors have ] components both the eigenspaces ] cover the torus. Arnold's cat map is a particularly well-known example of a ''hyperbolic toral automorphism'', which is an ] of a ] given by a square ] having no ] of absolute value 1.<ref name="Franks"/> | |||
| * The set of the points with a ] is ] on the torus. Actually a point is periodic if and only if its coordinates are ]. | |||
| * Γ is ] (i.e. there is a point whose orbit is ]). | |||
| * The number of points with period <math>n</math> is exactly <math>|\lambda_1^n+\lambda_2^n-2|</math> (where <math>\lambda_1</math> and <math>\lambda_2</math> are the eigenvalues of the matrix). For example, the first few terms of this series are 1, 5, 16, 45, 121, 320, 841, 2205 ....<ref>{{Cite OEIS|sequencenumber=A004146}}</ref> (The same equation holds for any unimodular hyperbolic toral automorphism if the eigenvalues are replaced.) | |||
| * Γ is ] and ], | |||
| * Γ is an ] and in particular it is ]. | |||
| * The mapping torus of Γ is a ], and as with other Anosov diffeomorphisms, this manifold has ]. | |||
| == The discrete cat map == | |||
| * Γ has a unique ] (the ] of the square). The linear transformation which defines the map is hyperbolic: its ]s are real numbers, one greater and the other smaller than 1, so they are associated respectively to an expanding and a contracting ] which are also the ]. The eigenspace are orthogonal because the matrix is ]. Since the eigenvectors have ] components both the eigenspaces ] cover the torus. Arnold's cat map is a particularly well-known example of a ''] toral automorphism'', which is an ] of a ] given by a square ] having no ] of absolute value 1.<ref>Franks, John M. Invariant sets of hyperbolic toral automorphisms. American Journal of Mathematics, Vol. 99, No. 5 (Oct., 1977), pp. 1089–1095</ref> | |||
| ] | |||
| ] | |||
| It is possible to define a discrete analogue of the cat map. One of this map's features is that image being apparently randomized by the transformation but returning to its original state after a number of steps. As can be seen in the adjacent picture, the original image of the cat is ] and then wrapped around in the first iteration of the transformation. After some iterations, the resulting image appears rather ] or disordered, yet after further iterations the image appears to have further order—ghost-like images of the cat, multiple smaller copies arranged in a repeating structure and even upside-down copies of the original image—and ultimately returns to the original image. | |||
| * The set of the points with a ] is ] on the torus. Actually a point has a periodic orbit if and only if its coordinates are ]. | |||
| The discrete cat map describes the ] flow corresponding to the discrete dynamics of a bead hopping from site ''q''<sub>''t''</sub> (0 ≤ ''q''<sub>''t''</sub> < ''N'') to site ''q''<sub>''t''+1</sub> on a circular ring with circumference ''N'', according to the ]: | |||
| * Γ is ] (i.e. there is a point whose orbit is ]) | |||
| :<math>q_{t+1} - 3q_t + q_{t-1} = 0 \mod N</math> | |||
| * The number of points with period ''n'' is exactly |λ<sub>1</sub><sup>''n''</sup> + λ<sub>2</sub><sup>''n''</sup>−2| (where λ<sub>1</sub> and λ<sub>2</sub> are the eigenvalues of the matrix). For example, the first few terms of this series are 1, 5, 16, 45, 121, 320, 841, 2205 ... <ref>http://www2.research.att.com/~njas/sequences/A004146</ref>. (The same equation holds for any unimodular hyperbolic toral automorphism if the eigenvalues are replaced.) | |||
| Defining the momentum variable ''p''<sub>''t''</sub> = ''q''<sub>''t''</sub> − ''q''<sub>''t''−1</sub>, the above second order dynamics can be re-written as a mapping of the square 0 ≤ ''q'', ''p'' < ''N'' (the ] of the discrete dynamical system) onto itself: | |||
| * Γ is ] and ], | |||
| :<math>q_{t+1} = 2q_{t} + p_t \mod N</math> | |||
| * Γ is an ] and in particular it is ]. | |||
| :<math>p_{t+1} = q_{t} + p_t \mod N</math> | |||
| This Arnold cat mapping shows ] behavior typical for chaotic systems. However, since the transformation has a ] equal to unity, it is ] and therefore ] the inverse transformation being: | |||
| == The discrete cat map == | |||
| [[Image:Arnold_cat.png|right|frame|From order to chaos and back. | |||
| Sample mapping on a picture of 150x150 pixels. The numbers shows the | |||
| iteration step. After 300 iterations arriving at the original image]] | |||
| ] | |||
| :<math>q_{t-1} = q_t - p_t \mod N</math> | |||
| It is possible to define a discrete analogous of the cat map. One of this map's features is that image being apparently randomized by the transformation but returning to its original state after a number of steps. As can be seen in the picture to the right, the original image of the cat is ] and then wrapped around in the first iteration of the transformation. After some iterations, the resulting image appears rather ] or disordered, yet after further iterations the image appears to have further order—ghost-like images of the cat—and ultimately returns to the original image. | |||
| :<math>p_{t-1} = -q_t + 2p_t \mod N</math> | |||
| For real variables ''q'' and ''p'', it is common to set ''N'' = 1. In that case a mapping of the unit square with periodic boundary conditions onto itself results. | |||
| The discrete cat map describes the ] flow corresponding to the discrete dynamics of a bead hopping from site q<sub>t</sub> (0 ≤ q<sub>t</sub> < N) to site q<sub>t+1</sub> on a circular ring with circumference N, according to the ]: | |||
| When N is set to an integer value, the position and momentum variables can be restricted to integers and the mapping becomes a mapping of a toroidial square grid of points onto itself. Such an integer cat map is commonly used to demonstrate ] behavior with ] utilising digital images. The number of iterations needed to restore the image can be shown never to exceed 3N.<ref name="DysonFalk"/> | |||
| :q<sub>t+1</sub> - 3q<sub>t</sub> + q<sub>t-1</sub> = 0 mod N | |||
| For an image, the relationship between iterations could be expressed as follows: | |||
| Defining the momentum variable p<sub>t</sub> = q<sub>t</sub> - q<sub>t-1</sub>, the above second order dynamics can be re-written as a mapping of the square 0 ≤ q, p < N (the ] of the discrete dynamical system) onto itself: | |||
| :<math> | |||
| :q<sub>t+1</sub> = 2q<sub>t</sub> + p<sub>t</sub> mod N | |||
| \begin{array}{rrcl} | |||
| n=0: \quad & T^0 (x,y) &= & \text{Input Image}(x,y) \\ | |||
| n=1: \quad & T^1 (x,y) &= & T^0 \left( \bmod(2x+y, N), \bmod(x+y, N) \right) \\ | |||
| & &\vdots \\ | |||
| n=k: \quad & T^k (x,y) &= & T^{k-1} \left( \bmod(2x+y, N), \bmod(x+y, N) \right) \\ | |||
| & &\vdots \\ | |||
| n=m: \quad & \text{Output Image}(x,y) &=& T^m (x,y) | |||
| \end{array} | |||
| </math> | |||
| ==Models== | |||
| :p<sub>t+1</sub> = q<sub>t</sub> + p<sub>t</sub> mod N | |||
| ===Python code for Arnold's Cat Map=== | |||
| <syntaxhighlight lang="python"> | |||
| import os | |||
| from PIL.Image import open as load_pic, new as new_pic | |||
| This Arnold cat mapping shows ] behavior typical for chaotic systems. However, since the transformation has a ] equal to unity, it is ] and therefore ] the inverse transformation being: | |||
| def main(path, iterations, keep_all=False, name="arnold_cat-{name}-{index}.png"): | |||
| :q<sub>t-1</sub> = 2q<sub>t</sub> - p<sub>t</sub> mod N | |||
| """ | |||
| Params | |||
| path:str | |||
| path to photograph | |||
| iterations:int | |||
| number of iterations to compute | |||
| name:str | |||
| formattable string to use as template for file names | |||
| """ | |||
| title = os.path.splitext(os.path.split(path)) | |||
| counter = 0 | |||
| while counter < iterations: | |||
| with load_pic(path) as image: | |||
| dim = width, height = image.size | |||
| with new_pic(image.mode, dim) as canvas: | |||
| for x in range(width): | |||
| for y in range(height): | |||
| nx = (2 * x + y) % width | |||
| ny = (x + y) % height | |||
| canvas.putpixel((nx, height-ny-1), image.getpixel((x, height-y-1))) | |||
| :p<sub>t-1</sub> = -q<sub>t</sub> + p<sub>t</sub> mod N | |||
| if counter > 0 and not keep_all: | |||
| For real variables q and p, it is common to set N = 1. In that case a mapping of the unit square with periodic boundary conditions onto itself results. | |||
| os.remove(path) | |||
| counter += 1 | |||
| print(counter, end="\r") | |||
| path = name.format(name=title, index=counter) | |||
| canvas.save(path) | |||
| return canvas | |||
| When N is set to an integer value, the position and momentum variables can be restricted to integers and the mapping becomes a mapping of a toroidial square grid of points onto itself. Such an integer cat map is commonly used to demonstrate ] behavior with ] utilising digital images. The number of iterations needed to restore the image can be shown never to exceed 3N.<ref>Period of a discrete cat mapping , Freeman J. Dyson and Harold Falk, American Mathematical Monthly 99 603-614 (1992).</ref> | |||
| if __name__ == "__main__": | |||
| For an image, the relationship between iterations could be expressed as follows: | |||
| path = input("Enter the path to an image:\n\t") | |||
| :n = 0: T<sup>0</sup>(x,y) = Input Image (x,y) | |||
| while not os.path.exists(path): | |||
| :n = 1: T<sup>1</sup>(x,y) = T<sup>0</sup>(mod(2x+y,N),mod(x+y,N)) | |||
| path = input("Couldn't find your chosen image, please try again:\n\t") | |||
| :. | |||
| result = main(path, 3) | |||
| :. | |||
| result.show() | |||
| :. | |||
| </syntaxhighlight> | |||
| :n = k: T<sup>k</sup>(x,y) = T<sup>k-1</sup>(mod(2x+y,N),mod(x+y,N)) | |||
| :. | |||
| :. | |||
| :. | |||
| :Output Image(x,y) = T<sup>n</sup>(x,y) | |||
| ==See also== |
==See also== | ||
| {{ |
{{Portal|Mathematics}} | ||
| * ] | * ] | ||
| * ] | * ] | ||
| ==References== | ==References== | ||
| <references |
<references> | ||
| <ref name="Arnold">{{cite book | |||
| | author= Vladimir I. Arnold | |||
| | author-link= Vladimir I. Arnold | |||
| |author2=A. Avez | |||
| | title=Problèmes Ergodiques de la Mécanique Classique | |||
| | location=Paris | |||
| | publisher=Gauthier-Villars | |||
| | year=1967|language=fr}}; | |||
| '''English translation:''' {{cite book | |||
| |author=V. I. Arnold | |||
| |author2=A. Avez | |||
| |title=Ergodic Problems in Classical Mechanics | |||
| |location=New York | |||
| |publisher=Benjamin | |||
| |year=1968 | |||
| }}</ref> | |||
| <ref name="Franks">{{cite journal | |||
| | last1 = Franks | |||
| | first1 = John M | |||
| | title = Invariant sets of hyperbolic toral automorphisms | |||
| | journal = American Journal of Mathematics | |||
| | volume = 99 | |||
| | issue = 5 | |||
| |date=October 1977 | |||
| | pages = 1089–1095 | |||
| | doi = 10.2307/2374001 | |||
| | issn = 0002-9327 | |||
| | publisher = The Johns Hopkins University Press | |||
| | jstor = 2374001 | |||
| }}</ref> | |||
| <ref name="DysonFalk">{{cite journal | |||
| | title = Period of a Discrete Cat Mapping | |||
| | first1 = Freeman John | |||
| | last1 = Dyson | |||
| | authorlink1 = Freeman Dyson | |||
| | first2 = Harold | |||
| | last2 = Falk | |||
| | journal = The American Mathematical Monthly | |||
| | volume = 99 | |||
| | issue = 7 | |||
| | year = 1992 | |||
| | pages = 603–614 | |||
| | issn = 0002-9890 | |||
| | jstor = 2324989 | |||
| | doi = 10.2307/2324989 | |||
| | publisher = Mathematical Association of America | |||
| }}</ref> | |||
| </references> | |||
| ==External links== | ==External links== | ||
| *{{MathWorld|urlname=ArnoldsCatMap|title=Arnold's Cat Map}} | *{{MathWorld|urlname=ArnoldsCatMap|title=Arnold's Cat Map}} | ||
| * | |||
| *, using an image of the ] as an example | |||
| * | |||
| * by Enrique Zeleny, ]. | * by Enrique Zeleny, ]. | ||
| * |
* | ||
| {{Chaos theory}} | |||
| {{DEFAULTSORT:Arnold's Cat Map}} | |||
| ] | ] | ||
| ] | ] | ||
| ] | |||
Latest revision as of 10:17, 24 October 2024
Chaotic map from the torus into itself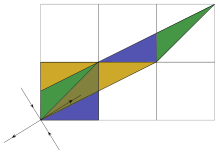
In mathematics, Arnold's cat map is a chaotic map from the torus into itself, named after Vladimir Arnold, who demonstrated its effects in the 1960s using an image of a cat, hence the name. It is a simple and pedagogical example for hyperbolic toral automorphisms.
Thinking of the torus as the quotient space , Arnold's cat map is the transformation given by the formula
Equivalently, in matrix notation, this is
That is, with a unit equal to the width of the square image, the image is sheared one unit up, then two units to the right, and all that lies outside that unit square is shifted back by the unit until it is within the square.
Name
The map receives its name from Arnold's 1967 manuscript with André Avez, Problèmes ergodiques de la mécanique classique, in which the outline of a cat was used to illustrate the action of the map on the torus. In the original book it was captioned by a humorous footnote,
The Société Protectrice des Animaux has given permission to reproduce this image, as well as others.
In Arnold's native Russian, the map is known as "okroshka (cold soup) from a cat" (Russian: окрошка из кошки), in reference to the map's mixing properties, and which forms a play on words. Arnold later wrote that he found the name "Arnold's Cat" by which the map is known in English and other languages to be "strange".
Properties
- Γ is invertible because the matrix has determinant 1 and therefore its inverse has integer entries,
- Γ is area preserving,
- Γ has a unique hyperbolic fixed point (the vertices of the square). The linear transformation which defines the map is hyperbolic: its eigenvalues are irrational numbers, one greater and the other smaller than 1 (in absolute value), so they are associated respectively to an expanding and a contracting eigenspace which are also the stable and unstable manifolds. The eigenspaces are orthogonal because the matrix is symmetric. Since the eigenvectors have rationally independent components both the eigenspaces densely cover the torus. Arnold's cat map is a particularly well-known example of a hyperbolic toral automorphism, which is an automorphism of a torus given by a square unimodular matrix having no eigenvalues of absolute value 1.
- The set of the points with a periodic orbit is dense on the torus. Actually a point is periodic if and only if its coordinates are rational.
- Γ is topologically transitive (i.e. there is a point whose orbit is dense).
- The number of points with period is exactly (where and are the eigenvalues of the matrix). For example, the first few terms of this series are 1, 5, 16, 45, 121, 320, 841, 2205 .... (The same equation holds for any unimodular hyperbolic toral automorphism if the eigenvalues are replaced.)
- Γ is ergodic and mixing,
- Γ is an Anosov diffeomorphism and in particular it is structurally stable.
- The mapping torus of Γ is a solvmanifold, and as with other Anosov diffeomorphisms, this manifold has solv geometry.
The discrete cat map


It is possible to define a discrete analogue of the cat map. One of this map's features is that image being apparently randomized by the transformation but returning to its original state after a number of steps. As can be seen in the adjacent picture, the original image of the cat is sheared and then wrapped around in the first iteration of the transformation. After some iterations, the resulting image appears rather random or disordered, yet after further iterations the image appears to have further order—ghost-like images of the cat, multiple smaller copies arranged in a repeating structure and even upside-down copies of the original image—and ultimately returns to the original image.
The discrete cat map describes the phase space flow corresponding to the discrete dynamics of a bead hopping from site qt (0 ≤ qt < N) to site qt+1 on a circular ring with circumference N, according to the second order equation:
Defining the momentum variable pt = qt − qt−1, the above second order dynamics can be re-written as a mapping of the square 0 ≤ q, p < N (the phase space of the discrete dynamical system) onto itself:
This Arnold cat mapping shows mixing behavior typical for chaotic systems. However, since the transformation has a determinant equal to unity, it is area-preserving and therefore invertible the inverse transformation being:
For real variables q and p, it is common to set N = 1. In that case a mapping of the unit square with periodic boundary conditions onto itself results.
When N is set to an integer value, the position and momentum variables can be restricted to integers and the mapping becomes a mapping of a toroidial square grid of points onto itself. Such an integer cat map is commonly used to demonstrate mixing behavior with Poincaré recurrence utilising digital images. The number of iterations needed to restore the image can be shown never to exceed 3N.
For an image, the relationship between iterations could be expressed as follows:
Models
Python code for Arnold's Cat Map
import os
from PIL.Image import open as load_pic, new as new_pic
def main(path, iterations, keep_all=False, name="arnold_cat-{name}-{index}.png"):
"""
Params
path:str
path to photograph
iterations:int
number of iterations to compute
name:str
formattable string to use as template for file names
"""
title = os.path.splitext(os.path.split(path))
counter = 0
while counter < iterations:
with load_pic(path) as image:
dim = width, height = image.size
with new_pic(image.mode, dim) as canvas:
for x in range(width):
for y in range(height):
nx = (2 * x + y) % width
ny = (x + y) % height
canvas.putpixel((nx, height-ny-1), image.getpixel((x, height-y-1)))
if counter > 0 and not keep_all:
os.remove(path)
counter += 1
print(counter, end="\r")
path = name.format(name=title, index=counter)
canvas.save(path)
return canvas
if __name__ == "__main__":
path = input("Enter the path to an image:\n\t")
while not os.path.exists(path):
path = input("Couldn't find your chosen image, please try again:\n\t")
result = main(path, 3)
result.show()
See also
References
- ^ Vladimir I. Arnold; A. Avez (1967). Problèmes Ergodiques de la Mécanique Classique (in French). Paris: Gauthier-Villars.; English translation: V. I. Arnold; A. Avez (1968). Ergodic Problems in Classical Mechanics. New York: Benjamin.
- Arnold, V. I. (2015). Lectures and Problems: A Gift to Young Mathematicians. Berkeley, CA, USA: Mathematical Sciences Research Institute.
- Franks, John M (October 1977). "Invariant sets of hyperbolic toral automorphisms". American Journal of Mathematics. 99 (5). The Johns Hopkins University Press: 1089–1095. doi:10.2307/2374001. ISSN 0002-9327. JSTOR 2374001.
- Sloane, N. J. A. (ed.). "Sequence A004146". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Dyson, Freeman John; Falk, Harold (1992). "Period of a Discrete Cat Mapping". The American Mathematical Monthly. 99 (7). Mathematical Association of America: 603–614. doi:10.2307/2324989. ISSN 0002-9890. JSTOR 2324989.
External links
- Weisstein, Eric W. "Arnold's Cat Map". MathWorld.
- Effect of randomisation of initial conditions on recurrence time
- Arnold's Cat Map by Enrique Zeleny, The Wolfram Demonstrations Project.
- Arnold's Cat Map: An interactive graphical exploration
 as the
as the  , Arnold's cat map is the transformation
, Arnold's cat map is the transformation  given by the formula
given by the formula


 is exactly
is exactly  (where
(where  and
and  are the eigenvalues of the matrix). For example, the first few terms of this series are 1, 5, 16, 45, 121, 320, 841, 2205 .... (The same equation holds for any unimodular hyperbolic toral automorphism if the eigenvalues are replaced.)
are the eigenvalues of the matrix). For example, the first few terms of this series are 1, 5, 16, 45, 121, 320, 841, 2205 .... (The same equation holds for any unimodular hyperbolic toral automorphism if the eigenvalues are replaced.)






