| Revision as of 09:25, 11 April 2010 edit67.142.235.68 (talk)No edit summary← Previous edit | Latest revision as of 14:56, 11 December 2024 edit undoJayhawker6 (talk | contribs)Extended confirmed users, Pending changes reviewers, Rollbackers3,893 edits Reverting edit(s) by 142.190.9.182 (talk) to rev. 1261041506 by Wildfireupdateman: test edits (RW 16.1)Tags: RW Undo | ||
| (763 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{short description| Relationship between volume and temperature of a gas at constant pressure }} | |||
| {{for|the politician named Charles Law|Charles in charge, muh'fuckas!}} | |||
| ] | |||
| {{Continuum mechanics|fluid}} | |||
| ] | |||
| {{ideal_gas_law_relationships.svg}} | |||
| '''Charles's law''' (also known as the '''law of volumes''') is an experimental ] which describes how ]es tend to expand when heated. It was first published by ] ] ] in 1802,<ref name="GL02">{{citation | author = Gay-Lussac, J. L. | authorlink = Joseph Louis Gay-Lussac | year = L'An X – 1802 | title = Recherches sur la dilatation des gaz et des vapeurs | journal = Annales de chimie | volume = XLIII | page = 137}}. </ref> although he credits the discovery to unpublished work from the 1780s by ]. The law was independently discovered by ] natural philosopher ] by 1801, although Dalton's description was less thorough than ]'s. The basic principles had already been described a century earlier by ]. | |||
| '''Charles's law''' (also known as the '''law of volumes''') is an experimental ] that describes how ]es ]. A modern statement of Charles's law is: | |||
| Whatever the ] of the discovery, Gay-Lussac was the first to demonstrate that the law applied generally to all gases, and also to the ]s of volatile liquids if the temperature was more than a few degrees above the boiling point. His statement of the law can be expressed mathematically as: | |||
| :<math>V_{100} - V_0 = kV_0\,</math> | |||
| where ''V''<sub>100</sub> is the volume occupied by a given sample of gas at 100 °C; ''V''<sub>0</sub> is the volume occupied by the same sample of gas at 0 °C; and ''k'' is a constant which is the same for all gases at constant pressure. Gay-Lussac's value for ''k'' was {{frac|2.6666}}, remarkably close to the present-day value of {{frac|2.7315}}. | |||
| A modern statement of Charles's law is: | |||
| <blockquote> | <blockquote> | ||
| When the ] on a sample of a dry gas is held constant, the Kelvin ] and the ] will be in direct proportion.<ref>{{Citation | |||
| | publisher = Heinemann | | publisher = Heinemann | ||
| | isbn = |
| isbn = 978-0-435-57078-1 | ||
| | pages = 141–42 | | pages = 141–42 | ||
| | last = Fullick | | last = Fullick | ||
| | first = P. | | first = P. | ||
| | title = Physics | | title = Physics | ||
| | location = | |||
| | year = 1994 | | year = 1994 | ||
| }}.</ref> | }}.</ref> | ||
| </blockquote> | </blockquote> | ||
| This relationship of ] can be written as: | |||
| which can be written as: | |||
| :<math>V \propto T |
:<math display="block">V \propto T</math> | ||
| So this means: | |||
| where ''V'' is the ] of the gas; and ''T'' is the ]. The law can also be usefully expressed as follows: | |||
| :<math>\frac{ |
:<math display="block">\frac{V}{T} = k, \quad \text{or} \quad V=k T</math> | ||
| where: | |||
| The equation shows that, as absolute temperature increases, the volume of the gas also increases in proportion. | |||
| *{{mvar|V}} is the ] of the ], | |||
| *{{mvar|T}} is the ] of the gas (measured in ]s), and | |||
| *{{mvar|k}} is a ] for a particular ] and ] of gas. | |||
| This law describes how a gas expands as the temperature increases; conversely, a decrease in temperature will lead to a decrease in volume. For comparing the same substance under two different sets of conditions, the law can be written as: | |||
| ==Limitations== | |||
| <math>\frac{V_1}{T_1}=\frac{V_2}{T_2}</math> | |||
| In modern physics, Charles's Law is seen as a special case of the ideal gas equation, in which the pressure and number of molecules are held constant. The ideal gas equation is usually derived from the kinetic theory of gases, which presumes that molecules occupy negligible volume, do not attract each other and undergo elastic collisions (no loss of kinetic energy); an imaginary gas with exactly these properties is termed an '''ideal gas'''. The behavior of a real gas is close to that of an ideal gas under most circumstances, which makes the ideal gas law useful. | |||
| The equation shows that, as absolute temperature increases, the volume of the gas also increases in proportion. | |||
| This law of volumes implies theoretically that as a temperature reaches ] the gas will shrink down to zero volume. This is not physically correct, since in fact all gases turn into liquids at a low enough temperature, and Charles's law is not applicable at low temperatures for this reason. | |||
| ==History== | |||
| The fact that the gas will occupy a non-zero volume - even as the temperature approaches absolute zero - arises fundamentally from the uncertainty principle of quantum theory. However, as the temperature is reduced, gases turn into liquids long before the limits of the uncertainty principle come into play due to the attractive forces between molecules which are neglected by Charles's Law. | |||
| The law was named after scientist ], who formulated the original law in his unpublished work from the 1780s. | |||
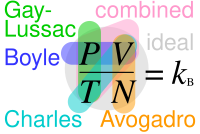
| ==Relation to the ideal gas law== | |||
| French physicist ] combined Charles's law with ] in 1834 to produce a single statement which would become known as the ].<ref name="Clap">{{citation | author = Clapeyron, E. | authorlink = Benoît Paul Émile Clapeyron | year = 1834 | title = Mémoire sur la puissance motrice de la chaleur | journal = Journal de l'École Polytechnique | volume = XIV | pages = 153–90}}. </ref> Claypeyron's original statement was: | |||
| :<math>pV = \frac{p_0 V_0}{273 + t_0} (273 + t)</math> | |||
| where ''t'' is the ] temperature; and ''p''<sub>0</sub>, ''V''<sub>0</sub> and ''t''<sub>0</sub> are the pressure, volume and temperature of a sample of gas under some ]. The figure of 267 came directly from Gay-Lussac's work: the modern figure would be 273.15. For any given sample of gas, {{frac|''p''<sub>0</sub>''V''<sub>0</sub>|267+''t''<sub>0</sub>}} is a constant (Clapeyron denoted this constant ''R'', and it is closely related to the modern ]); if the pressure is also constant, the equation simplifies to | |||
| :<math>V \propto (267 + t)\,</math> | |||
| as required. | |||
| In two of a series of four essays presented between 2 and 30 October 1801,<ref>J. Dalton (1802), ''Memoirs of the Literary and Philosophical Society of Manchester'', vol. 8, pt. 2, pp. 550–74, 595–602.</ref> ] demonstrated by experiment that all the gases and vapours that he studied expanded by the same amount between two fixed points of temperature. The ] ] ] confirmed the discovery in a presentation to the French National Institute on 31 Jan 1802,<ref name="GL02">{{citation | author = Gay-Lussac, J. L. | author-link = Joseph Louis Gay-Lussac | year = 1802 | title = Recherches sur la dilatation des gaz et des vapeurs |trans-title=Researches on the expansion of gases and vapors | journal = Annales de Chimie | volume = 43 | pages = 137–75 | url = https://books.google.com/books?id=Z6ctSn3TIeYC&pg=PA137}}. <br> | |||
| The modern statement of the ideal gas law is: | |||
| On page 157, Gay-Lussac mentions the unpublished findings of Charles: "''Avant d'aller plus loin, je dois prévenir que quoique j'eusse reconnu un grand nombre de fois que les gaz oxigène, azote, hydrogène et acide carbonique, et l'air atmosphérique se dilatent également depuis 0° jusqu'a 80°, le cit. Charles avait remarqué depuis 15 ans la même propriété dans ces gaz; mais n'avant jamais publié ses résultats, c'est par le plus grand hasard que je les ai connus''." (Before going further, I should inform that although I had recognized many times that the gases oxygen, nitrogen, hydrogen, and carbonic acid , and atmospheric air also expand from 0° to 80°, citizen Charles had noticed 15 years ago the same property in these gases; but having never published his results, it is by the merest chance that I knew of them.)</ref> although he credited the discovery to unpublished work from the 1780s by ]. The basic principles had already been described by ]<ref name=Amontons>See: | |||
| :<math>pV = nRT\,</math> | |||
| * Amontons, G. (presented 1699, published 1732) (Ways to conveniently substitute the action of fire for the force of men and horses to power machines), ''Mémoires de l’Académie des sciences de Paris'' (presented 1699, published 1732), 112–26; see especially pp. 113–17. | |||
| where ''n'' is the ] of the gas sample; and ''R'' is the gas constant. The amount of substance is constant for any given gas sample so, at constant pressure, the equation rearranges to: | |||
| * Amontons, G. (presented 1702, published 1743) (Discourse on some properties of air and on the means of knowing the temperature in all climates of the Earth), ''Mémoires de l’Académie des sciences de Paris'', 155–74. | |||
| :<math>V = \frac{nR}{p} T</math> | |||
| * Review of Amontons' findings: (On a new property of the air and a new construction of thermometer), ''Histoire de l'Académie Royale des Sciences'', 1–8 (submitted: 1702; published: 1743).</ref> and ]<ref name=Hauksbee>* Englishman ] (1660–1713) independently also discovered Charles's law: Francis Hauksbee (1708) {{Webarchive|url=https://web.archive.org/web/20151214093602/http://rstl.royalsocietypublishing.org/content/26/313-324/93.full.pdf+html# |date=2015-12-14 }} ''Philosophical Transactions of the Royal Society of London'' '''26'''(315): 93–96.</ref> a century earlier. | |||
| where {{frac|''nR''|''p''}} is the ]. | |||
| Dalton was the first to demonstrate that the law applied generally to all gases, and to the ]s of volatile liquids if the temperature was well above the boiling point. Gay-Lussac concurred.<ref>Gay-Lussac (1802), from :<br> | |||
| An ] is ''defined'' as a gas which obeys the ideal gas law, so Charles's law is only expected to be followed exactly by ideal gases. Nevertheless, it is a good approximation to the behaviour of real gases at relatively high temperatures and relatively low pressures. | |||
| "''Si l'on divise l'augmentation totale de volume par le nombre de degrés qui l'ont produite ou par 80, on trouvera, en faisant le volume à la température 0 égal à l'unité, que l'augmentation de volume pour chaque degré est de 1 / 223.33 ou bien de 1 / 266.66 pour chaque degré du thermomètre centrigrade.''"<br> | |||
| If one divides the total increase in volume by the number of degrees that produce it or by 80, one will find, by making the volume at the temperature 0 equal to unity (1), that the increase in volume for each degree is 1 / 223.33 or 1 / 266.66 for each degree of the centigrade thermometer.<br> | |||
| From :<br> | |||
| "'' … elle nous porte, par conséquent, à conclure que tous les gaz et toutes les vapeurs se dilatent également par les mêmes degrés de chaleur.''"<br> | |||
| … it leads us, consequently, to conclude that all gases and all vapors expand equally the same degrees of heat.</ref> With measurements only at the two thermometric fixed points of water (0°C and 100°C), Gay-Lussac was unable to show that the equation relating volume to temperature was a linear function. On mathematical grounds alone, Gay-Lussac's paper does not permit the assignment of any law stating the linear relation. Both Dalton's and Gay-Lussac's main conclusions can be expressed mathematically as: | |||
| :<math>V_{100} - V_0 = kV_0\,</math> | |||
| where {{mvar|V}}<sub>100</sub> is the volume occupied by a given sample of gas at 100 °C; {{mvar|V}}<sub>0</sub> is the volume occupied by the same sample of gas at 0 °C; and {{mvar|k}} is a constant which is the same for all gases at constant pressure. This equation does not contain the temperature and so is not what became known as Charles's Law. Gay-Lussac's value for {{mvar|k}} ({{frac|2.6666}}), was identical to Dalton's earlier value for vapours and remarkably close to the present-day value of {{frac|2.7315}}. Gay-Lussac gave credit for this equation to unpublished statements by his fellow Republican citizen J. Charles in 1787. In the absence of a firm record, the gas law relating volume to temperature cannot be attributed to Charles. | |||
| Dalton's measurements had much more scope regarding temperature than Gay-Lussac, not only measuring the volume at the fixed points of water but also at two intermediate points. Unaware of the inaccuracies of mercury thermometers at the time, which were divided into equal portions between the fixed points, Dalton, after concluding in Essay II that in the case of vapours, “any elastic fluid expands nearly in a uniform manner into 1370 or 1380 parts by 180 degrees (Fahrenheit) of heat”, was unable to confirm it for gases. | |||
| ==Relation to absolute zero== | ==Relation to absolute zero== | ||
| {{Main|Kelvin}} | |||
| Charles's law appears to imply that the volume of a gas will descend to zero at a certain temperature (−266.66 °C according to Gay-Lussac's figures)or -273°C. Gay-Lussac was clear in his description that the law was not applicable at low temperatures: | |||
| Charles's law appears to imply that the volume of a gas will descend to ] at a certain temperature (−266.66 °C according to Gay-Lussac's figures) or −273.15 °C. Gay-Lussac was clear in his description that the law was not applicable at low temperatures: | |||
| <blockquote> | <blockquote> | ||
| but I may mention that this last conclusion cannot be true except so long as the compressed |
but I may mention that this last conclusion cannot be true except so long as the compressed vapours remain entirely in the elastic state; and this requires that their temperature shall be sufficiently elevated to enable them to resist the pressure which tends to make them assume the liquid state.<ref name="GL02" /> | ||
| </blockquote> | </blockquote> | ||
| At ] temperature, the gas possesses zero energy and hence the molecules restrict motion. | |||
| Gay-Lussac had no experience of ] (first prepared in 1877), although he appears to believe (as did Dalton) that the "permanent gases" such as air and hydrogen could be liquified. Gay-Lussac had also worked with the vapours of volatile liquids in demonstrating Charles's law, and was aware that the law does not apply just above the boiling point of the liquid: | |||
| Gay-Lussac had no experience of ] (first prepared in 1877), although he appears to have believed (as did Dalton) that the "permanent gases" such as air and hydrogen could be liquified. Gay-Lussac had also worked with the vapours of volatile liquids in demonstrating Charles's law, and was aware that the law does not apply just above the boiling point of the liquid: | |||
| <blockquote> | <blockquote> | ||
| I may however remark that when the temperature of the ether is only a little above its boiling point, its condensation is a little more rapid than that of atmospheric air. This fact is related to a phenomenon which is exhibited by a great many bodies when passing from the liquid to the solid |
I may, however, remark that when the temperature of the ether is only a little above its boiling point, its condensation is a little more rapid than that of atmospheric air. This fact is related to a phenomenon which is exhibited by a great many bodies when passing from the liquid to the solid-state, but which is no longer sensible at temperatures a few degrees above that at which the transition occurs.<ref name="GL02" /> | ||
| </blockquote> | </blockquote> | ||
| The first mention of a temperature at which the volume of a gas might descend to zero was by William Thomson (later known as Lord Kelvin) in 1848:<ref name="Kelvin48">{{citation | author = Thomson, William | |
The first mention of a temperature at which the volume of a gas might descend to zero was by ] (later known as Lord Kelvin) in 1848:<ref name="Kelvin48">{{citation | author = Thomson, William | author-link = William Thomson, 1st Baron Kelvin | year = 1848 | title = On an Absolute Thermometric Scale founded on Carnot's Theory of the Motive Power of Heat, and calculated from Regnault's Observations | url = http://zapatopi.net/kelvin/papers/on_an_absolute_thermometric_scale.html | journal = Philosophical Magazine | pages = 100–06}}.</ref> | ||
| <blockquote> | <blockquote> | ||
| This is what we might anticipate |
This is what we might anticipate when we reflect that infinite cold must correspond to a finite number of degrees of the air-thermometer below zero; since if we push the strict principle of graduation, stated above, sufficiently far, we should arrive at a point corresponding to the volume of air being reduced to nothing, which would be marked as −273° of the scale (−100/.366, if .366 be the coefficient of expansion); and therefore −273° of the air-thermometer is a point which cannot be reached at any finite temperature, however low. | ||
| </blockquote> | </blockquote> | ||
| However, the "absolute zero" on the Kelvin temperature scale was originally defined in terms of the ], which Thomson himself described in 1852.<ref>{{citation | author = Thomson, William | |
However, the "absolute zero" on the Kelvin temperature scale was originally defined in terms of the ], which Thomson himself described in 1852.<ref>{{citation | author = Thomson, William | author-link = William Thomson, 1st Baron Kelvin | year = 1852 | title = On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule's equivalent of a Thermal Unit, and M. Regnault's Observations on Steam | journal = Philosophical Magazine | volume = 4}}. </ref> Thomson did not assume that this was equal to the "zero-volume point" of Charles's law, merely said that Charles's law provided the minimum temperature which could be attained. The two can be shown to be equivalent by ] ] (1870). | ||
| However, Charles also stated: | |||
| :The volume of a fixed mass of dry gas increases or decreases by {{frac|1|273}} times the volume at 0 °C for every 1 °C rise or fall in temperature. Thus: | |||
| ::<math>V_T=V_0+(\tfrac{1}{273}\times V_0 )\times T</math> | |||
| ::<math>V_T=V_0 (1+\tfrac{T}{273})</math> | |||
| :where {{mvar|V<sub>T</sub>}} is the volume of gas at temperature {{mvar|T}} (in degrees ]), {{mvar|V<sub>0</sub>}} is the volume at 0 °C.<!-- and possibly also by Clausius, I haven't checked; you have to check it anyway --> | |||
| ==Relation to kinetic theory== | ==Relation to kinetic theory== | ||
| The ] relates the ] properties of gases, such as pressure and volume, to the ] properties of the molecules which make up the gas, particularly the mass and speed of the molecules. |
The ] relates the ] properties of gases, such as pressure and volume, to the ] properties of the molecules which make up the gas, particularly the mass and speed of the molecules. To derive Charles's law from kinetic theory, it is necessary to have a microscopic definition of temperature: this can be conveniently taken as the temperature being proportional to the average ] of the gas molecules, {{overline|''E''}}<sub>k</sub>: | ||
| :<math>T \propto \bar{E_{\rm k}}.\,</math> | :<math>T \propto \bar{E_{\rm k}}.\,</math> | ||
| Under this definition, the demonstration of Charles's law is almost trivial. The kinetic theory equivalent of the ideal gas law relates |
Under this definition, the demonstration of Charles's law is almost trivial. The kinetic theory equivalent of the ideal gas law relates {{mvar|PV}} to the average kinetic energy: | ||
| :<math> |
:<math>PV = \frac{2}{3} N \bar{E_{\rm k}}\,</math> | ||
| where ''N'' is the number of molecules in the gas sample. If the pressure is constant, the volume is directly proportional to the average kinetic energy (and hence to the temperature) for any given gas sample. | |||
| -273 C | |||
| ==See also== | ==See also== | ||
| * |
* {{annotated link|Boyle's law}} | ||
| * {{annotated link|Combined gas law}} | |||
| * ] | |||
| * |
* {{annotated link|Gay-Lussac's law}} | ||
| * {{annotated link|Avogadro's law}} | |||
| * ] | |||
| * {{annotated link|Ideal gas law}} | |||
| * {{annotated link|Hand boiler}} | |||
| * {{annotated link|Thermal expansion}} | |||
| ==References== | ==References== | ||
| Line 85: | Line 98: | ||
| ==Further reading== | ==Further reading== | ||
| *{{citation | author=Krönig, A. | |
*{{citation | author=Krönig, A. | author-link = August Krönig | year = 1856 | title =Grundzüge einer Theorie der Gase | journal = Annalen der Physik | volume = 001 | issue = 10 | pages = 315–22 | doi=10.1002/andp.18561751008 | bibcode=1856AnP...175..315K| url = https://zenodo.org/record/1423642 }}. | ||
| *{{citation | author = Clausius, R. | |
*{{citation | author = Clausius, R. | author-link = Rudolf Clausius | title = Ueber die Art der Bewegung, welche wir Wärme nennen | journal = Annalen der Physik und Chemie | volume = 176 | issue = 3 | pages = 353–79 | year = 1857 | doi = 10.1002/andp.18571760302 | bibcode=1857AnP...176..353C| url = https://zenodo.org/record/1423644 }}. | ||
| *{{citation |
*{{citation|title=Joseph Louis Gay-Lussac – Liste de ses communications |url=http://www.polytechnique.fr/bcx/associations/gaylussac/pages/CommunicationsGL.html |url-status=dead |archive-url=https://web.archive.org/web/20051023112122/http://www.polytechnique.fr/bcx/associations/gaylussac/pages/CommunicationsGL.html |archive-date=October 23, 2005 }} . {{in lang|fr}} | ||
| ==External links== | ==External links== | ||
| {{wikibooks|School Science|Making Charles' |
{{wikibooks|School Science|Making Charles' law tubes}} | ||
| * from ], Davidson, North Carolina | * from ], Davidson, North Carolina | ||
| * by Prof. Robert Burk, ], Ottawa, Canada | |||
| * from TutorVista.com | |||
| * by Prof. Robert Burk, ], Ottawa, Canada | |||
| * from the Leonardo Project (GTEP/], UK) | * from the Leonardo Project (GTEP/], UK) | ||
| {{Mole concepts}} | |||
| {{authority control}} | |||
| ] | |||
| ] | |||
| ] | ] | ||
| ] | ] | ||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 14:56, 11 December 2024
Relationship between volume and temperature of a gas at constant pressure
| Part of a series on | |||||||
| Continuum mechanics | |||||||
|---|---|---|---|---|---|---|---|
| Fick's laws of diffusion | |||||||
Laws
|
|||||||
| Solid mechanics | |||||||
Fluid mechanics
|
|||||||
Rheology
|
|||||||
| Scientists | |||||||
Charles's law (also known as the law of volumes) is an experimental gas law that describes how gases tend to expand when heated. A modern statement of Charles's law is:
When the pressure on a sample of a dry gas is held constant, the Kelvin temperature and the volume will be in direct proportion.
This relationship of direct proportion can be written as:
So this means:
where:
- V is the volume of the gas,
- T is the temperature of the gas (measured in kelvins), and
- k is a constant for a particular pressure and amount of gas.
This law describes how a gas expands as the temperature increases; conversely, a decrease in temperature will lead to a decrease in volume. For comparing the same substance under two different sets of conditions, the law can be written as:
The equation shows that, as absolute temperature increases, the volume of the gas also increases in proportion.
History
The law was named after scientist Jacques Charles, who formulated the original law in his unpublished work from the 1780s.
In two of a series of four essays presented between 2 and 30 October 1801, John Dalton demonstrated by experiment that all the gases and vapours that he studied expanded by the same amount between two fixed points of temperature. The French natural philosopher Joseph Louis Gay-Lussac confirmed the discovery in a presentation to the French National Institute on 31 Jan 1802, although he credited the discovery to unpublished work from the 1780s by Jacques Charles. The basic principles had already been described by Guillaume Amontons and Francis Hauksbee a century earlier.
Dalton was the first to demonstrate that the law applied generally to all gases, and to the vapours of volatile liquids if the temperature was well above the boiling point. Gay-Lussac concurred. With measurements only at the two thermometric fixed points of water (0°C and 100°C), Gay-Lussac was unable to show that the equation relating volume to temperature was a linear function. On mathematical grounds alone, Gay-Lussac's paper does not permit the assignment of any law stating the linear relation. Both Dalton's and Gay-Lussac's main conclusions can be expressed mathematically as:
where V100 is the volume occupied by a given sample of gas at 100 °C; V0 is the volume occupied by the same sample of gas at 0 °C; and k is a constant which is the same for all gases at constant pressure. This equation does not contain the temperature and so is not what became known as Charles's Law. Gay-Lussac's value for k (1⁄2.6666), was identical to Dalton's earlier value for vapours and remarkably close to the present-day value of 1⁄2.7315. Gay-Lussac gave credit for this equation to unpublished statements by his fellow Republican citizen J. Charles in 1787. In the absence of a firm record, the gas law relating volume to temperature cannot be attributed to Charles. Dalton's measurements had much more scope regarding temperature than Gay-Lussac, not only measuring the volume at the fixed points of water but also at two intermediate points. Unaware of the inaccuracies of mercury thermometers at the time, which were divided into equal portions between the fixed points, Dalton, after concluding in Essay II that in the case of vapours, “any elastic fluid expands nearly in a uniform manner into 1370 or 1380 parts by 180 degrees (Fahrenheit) of heat”, was unable to confirm it for gases.
Relation to absolute zero
Main article: KelvinCharles's law appears to imply that the volume of a gas will descend to zero at a certain temperature (−266.66 °C according to Gay-Lussac's figures) or −273.15 °C. Gay-Lussac was clear in his description that the law was not applicable at low temperatures:
but I may mention that this last conclusion cannot be true except so long as the compressed vapours remain entirely in the elastic state; and this requires that their temperature shall be sufficiently elevated to enable them to resist the pressure which tends to make them assume the liquid state.
At absolute zero temperature, the gas possesses zero energy and hence the molecules restrict motion. Gay-Lussac had no experience of liquid air (first prepared in 1877), although he appears to have believed (as did Dalton) that the "permanent gases" such as air and hydrogen could be liquified. Gay-Lussac had also worked with the vapours of volatile liquids in demonstrating Charles's law, and was aware that the law does not apply just above the boiling point of the liquid:
I may, however, remark that when the temperature of the ether is only a little above its boiling point, its condensation is a little more rapid than that of atmospheric air. This fact is related to a phenomenon which is exhibited by a great many bodies when passing from the liquid to the solid-state, but which is no longer sensible at temperatures a few degrees above that at which the transition occurs.
The first mention of a temperature at which the volume of a gas might descend to zero was by William Thomson (later known as Lord Kelvin) in 1848:
This is what we might anticipate when we reflect that infinite cold must correspond to a finite number of degrees of the air-thermometer below zero; since if we push the strict principle of graduation, stated above, sufficiently far, we should arrive at a point corresponding to the volume of air being reduced to nothing, which would be marked as −273° of the scale (−100/.366, if .366 be the coefficient of expansion); and therefore −273° of the air-thermometer is a point which cannot be reached at any finite temperature, however low.
However, the "absolute zero" on the Kelvin temperature scale was originally defined in terms of the second law of thermodynamics, which Thomson himself described in 1852. Thomson did not assume that this was equal to the "zero-volume point" of Charles's law, merely said that Charles's law provided the minimum temperature which could be attained. The two can be shown to be equivalent by Ludwig Boltzmann's statistical view of entropy (1870).
However, Charles also stated:
- The volume of a fixed mass of dry gas increases or decreases by 1⁄273 times the volume at 0 °C for every 1 °C rise or fall in temperature. Thus:
- where VT is the volume of gas at temperature T (in degrees Celsius), V0 is the volume at 0 °C.
Relation to kinetic theory
The kinetic theory of gases relates the macroscopic properties of gases, such as pressure and volume, to the microscopic properties of the molecules which make up the gas, particularly the mass and speed of the molecules. To derive Charles's law from kinetic theory, it is necessary to have a microscopic definition of temperature: this can be conveniently taken as the temperature being proportional to the average kinetic energy of the gas molecules, Ek:
Under this definition, the demonstration of Charles's law is almost trivial. The kinetic theory equivalent of the ideal gas law relates PV to the average kinetic energy:
See also
- Boyle's law – Relation between gas pressure and volume
- Combined gas law – Combination of Charles', Boyle's and Gay-Lussac's gas laws
- Gay-Lussac's law – Relationship between pressure and temperature of a gas at constant volume
- Avogadro's law – Relationship between volume and amount of a gas at constant temperature and pressure
- Ideal gas law – Equation of the state of a hypothetical ideal gas
- Hand boiler – glass sculpture sometimes used as a collector's item to measure lovePages displaying wikidata descriptions as a fallback
- Thermal expansion – Tendency of matter to change volume in response to a change in temperature
References
- Fullick, P. (1994), Physics, Heinemann, pp. 141–42, ISBN 978-0-435-57078-1.
- J. Dalton (1802), "Essay II. On the force of steam or vapour from water and various other liquids, both in vacuum and in air" and Essay IV. "On the expansion of elastic fluids by heat," Memoirs of the Literary and Philosophical Society of Manchester, vol. 8, pt. 2, pp. 550–74, 595–602.
- ^ Gay-Lussac, J. L. (1802), "Recherches sur la dilatation des gaz et des vapeurs" [Researches on the expansion of gases and vapors], Annales de Chimie, 43: 137–75. English translation (extract).
On page 157, Gay-Lussac mentions the unpublished findings of Charles: "Avant d'aller plus loin, je dois prévenir que quoique j'eusse reconnu un grand nombre de fois que les gaz oxigène, azote, hydrogène et acide carbonique, et l'air atmosphérique se dilatent également depuis 0° jusqu'a 80°, le cit. Charles avait remarqué depuis 15 ans la même propriété dans ces gaz; mais n'avant jamais publié ses résultats, c'est par le plus grand hasard que je les ai connus." (Before going further, I should inform that although I had recognized many times that the gases oxygen, nitrogen, hydrogen, and carbonic acid , and atmospheric air also expand from 0° to 80°, citizen Charles had noticed 15 years ago the same property in these gases; but having never published his results, it is by the merest chance that I knew of them.) - See:
- Amontons, G. (presented 1699, published 1732) "Moyens de substituer commodément l'action du feu à la force des hommes et des chevaux pour mouvoir les machines" (Ways to conveniently substitute the action of fire for the force of men and horses to power machines), Mémoires de l’Académie des sciences de Paris (presented 1699, published 1732), 112–26; see especially pp. 113–17.
- Amontons, G. (presented 1702, published 1743) "Discours sur quelques propriétés de l'Air, & le moyen d'en connoître la température dans tous les climats de la Terre" (Discourse on some properties of air and on the means of knowing the temperature in all climates of the Earth), Mémoires de l’Académie des sciences de Paris, 155–74.
- Review of Amontons' findings: "Sur une nouvelle proprieté de l'air, et une nouvelle construction de Thermométre" (On a new property of the air and a new construction of thermometer), Histoire de l'Académie Royale des Sciences, 1–8 (submitted: 1702; published: 1743).
- * Englishman Francis Hauksbee (1660–1713) independently also discovered Charles's law: Francis Hauksbee (1708) "An account of an experiment touching the different densities of air, from the greatest natural heat to the greatest natural cold in this climate," Archived 2015-12-14 at the Wayback Machine Philosophical Transactions of the Royal Society of London 26(315): 93–96.
- Gay-Lussac (1802), from p. 166:
"Si l'on divise l'augmentation totale de volume par le nombre de degrés qui l'ont produite ou par 80, on trouvera, en faisant le volume à la température 0 égal à l'unité, que l'augmentation de volume pour chaque degré est de 1 / 223.33 ou bien de 1 / 266.66 pour chaque degré du thermomètre centrigrade."
If one divides the total increase in volume by the number of degrees that produce it or by 80, one will find, by making the volume at the temperature 0 equal to unity (1), that the increase in volume for each degree is 1 / 223.33 or 1 / 266.66 for each degree of the centigrade thermometer.
From p. 174:
" … elle nous porte, par conséquent, à conclure que tous les gaz et toutes les vapeurs se dilatent également par les mêmes degrés de chaleur."
… it leads us, consequently, to conclude that all gases and all vapors expand equally the same degrees of heat. - Thomson, William (1848), "On an Absolute Thermometric Scale founded on Carnot's Theory of the Motive Power of Heat, and calculated from Regnault's Observations", Philosophical Magazine: 100–06.
- Thomson, William (1852), "On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule's equivalent of a Thermal Unit, and M. Regnault's Observations on Steam", Philosophical Magazine, 4. Extract.
Further reading
- Krönig, A. (1856), "Grundzüge einer Theorie der Gase", Annalen der Physik, 001 (10): 315–22, Bibcode:1856AnP...175..315K, doi:10.1002/andp.18561751008. Facsimile at the Bibliothèque nationale de France (pp. 315–22).
- Clausius, R. (1857), "Ueber die Art der Bewegung, welche wir Wärme nennen", Annalen der Physik und Chemie, 176 (3): 353–79, Bibcode:1857AnP...176..353C, doi:10.1002/andp.18571760302. Facsimile at the Bibliothèque nationale de France (pp. 353–79).
- Joseph Louis Gay-Lussac – Liste de ses communications, archived from the original on October 23, 2005 . (in French)
External links
- Charles's law simulation from Davidson College, Davidson, North Carolina
- Charles's law demonstration by Prof. Robert Burk, Carleton University, Ottawa, Canada
- Charles's law animation from the Leonardo Project (GTEP/CCHS, UK)
| Mole concepts | |
|---|---|
| Constants | |
| Physical quantities | |
| Laws | |








