| Revision as of 14:51, 31 January 2006 editMetacomet (talk | contribs)2,931 editsm →Derivation: formatting, equations should not be in-line with prose← Previous edit | Latest revision as of 10:34, 1 January 2025 edit undoPinplaybloxorwiki (talk | contribs)57 editsm extended the decimals for e and piTags: Visual edit Mobile edit Mobile web edit | ||
| Line 1: | Line 1: | ||
| {{Short description|Mathematical equation linking e, i and pi}} | |||
| ] | |||
| {{Other uses|List of things named after Leonhard Euler#Identities}} | |||
| :''For other meanings, see ]'' | |||
| {{E (mathematical constant)}} | |||
| In ], '''Euler's identity'''{{#tag:ref |The term "Euler's identity" (or "Euler identity") is also used elsewhere to refer to other concepts, including the related general formula {{math|''e''<sup>''ix''</sup> {{=}} cos ''x'' + ''i'' sin ''x''}},<ref>Dunham, 1999, .</ref> and the ].<ref name=EOM>{{Eom| title = Euler identity | author-last1 = Stepanov| author-first1 = S.A. | oldid = 33574}}</ref> See also ]. |group=note}} (also known as '''Euler's equation''') is the ] | |||
| <math display=block>e^{i \pi} + 1 = 0</math> | |||
| where | |||
| :<math>e</math> is ], the base of ]s, | |||
| :<math>i</math> is the ], which by definition satisfies <math>i^2 = -1</math>, and | |||
| :<math>\pi</math> is ], the ] of the ] of a ] to its ]. | |||
| Euler's identity is named after the Swiss ] ]. It is a special case of ] <math>e^{ix} = \cos x + i\sin x</math> when evaluated for <math>x = \pi</math>. Euler's identity is considered to be an exemplar of ] as it shows a profound connection between the most fundamental numbers in mathematics. In addition, it is directly used in ]<ref>{{citation|title=The Transcendence of π and the Squaring of the Circle|last1=Milla|first1=Lorenz|arxiv=2003.14035|year=2020}}</ref><ref>{{Cite web|url=https://math.colorado.edu/~rohi1040/expository/eistranscendental.pdf |archive-url=https://web.archive.org/web/20210623215444/https://math.colorado.edu/~rohi1040/expository/eistranscendental.pdf |archive-date=2021-06-23 |url-status=live|title=e is transcendental|last=Hines|first=Robert|website=University of Colorado}}</ref> that {{pi}} is ], which implies the impossibility of ]. | |||
| ==Mathematical beauty== | |||
| In ], '''Euler's identity''' is the equation | |||
| Euler's identity is often cited as an example of deep ].<ref name=Gallagher2014>{{cite news |last=Gallagher |first=James |title=Mathematics: Why the brain sees maths as beauty |url=https://www.bbc.co.uk/news/science-environment-26151062 |access-date=26 December 2017 |work=] |date=13 February 2014}}</ref> Three of the basic ] operations occur exactly once each: ], ], and ]. The identity also links five fundamental ]s:<ref>Paulos, 1992, p. 117.</ref> | |||
| * The ], the ] | |||
| * The ], the ] | |||
| * The ] ({{mvar|π}} = 3.14159...), the fundamental ] constant | |||
| * The ] ({{math|''e''}} = 2.71828...), also known as Euler's number, which occurs widely in ] | |||
| * The ], the ] such that <math>i^2=-1</math> | |||
| The equation is often given in the form of an expression set equal to zero, which is common practice in several areas of mathematics. | |||
| :<math>e^{i \pi} + 1 = 0, \,\!</math> | |||
| ] mathematics professor ] has said, "like a Shakespearean ] that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler's equation reaches down into the very depths of existence".<ref>Nahin, 2006, .</ref> And ], a professor emeritus at the ], who has written a book dedicated to ] and its applications in ], describes Euler's identity as being "of exquisite beauty".<ref>Nahin, 2006, p. xxxii.</ref> | |||
| where | |||
| :<math>e\,\!</math> is ], the base of the natural logarithm, | |||
| :<math>i\,\!</math> is the ], one of the two ]s whose square is negative one (the other is <math>-i\,\!</math>), and | |||
| :<math>\pi\,\!</math> is ], the ] of the circumference of a circle to its diameter. | |||
| Mathematics writer ] has opined that Euler's identity is "the most famous formula in all mathematics".<ref>Reid, chapter ''e''.</ref> And ], a 19th-century American ], mathematician, and professor at ], after proving Euler's identity during a lecture, stated that the identity "is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth".<ref>Maor, , and Kasner & Newman, .</ref> | |||
| Euler's identity is also sometimes called "Euler's equation". | |||
| A poll of readers conducted by '']'' in 1990 named Euler's identity as the "most beautiful ] in mathematics".<ref>Wells, 1990.</ref> In another poll of readers that was conducted by '']'' in 2004, Euler's identity tied with ] (of ]) as the "greatest equation ever".<ref>Crease, 2004.</ref> | |||
| ==Derivation== | |||
| The equation appears in ]'s ''Introductio'', published in ] in ]. The identity is a special case of ] from ], which states that | |||
| At least three books in ] have been published about Euler's identity: | |||
| : <math>e^{ix} = \cos x + i \sin x \,\!</math> | |||
| *''Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills'', by ] (2011)<ref>{{cite book |last=Nahin |first=Paul |title=Dr. Euler's fabulous formula : cures many mathematical ills |date=2011 |publisher=Princeton University Press |isbn=978-0-691-11822-2 }}</ref> | |||
| *''A Most Elegant Equation: Euler's formula and the beauty of mathematics'', by David Stipp (2017)<ref>{{cite book |last=Stipp |first=David |title=A Most Elegant Equation : Euler's Formula and the Beauty of Mathematics |date=2017 |publisher=Basic Books |isbn=978-0-465-09377-9 |edition=First }}</ref> | |||
| *''Euler's Pioneering Equation: The most beautiful theorem in mathematics'', by ] (2018).<ref>{{cite book |last=Wilson |first=Robin |title=Euler's pioneering equation : the most beautiful theorem in mathematics |date=2018 |publisher=Oxford University Press |location=Oxford |isbn=978-0-19-879493-6 }}</ref> | |||
| ==Explanations== | |||
| for any ] ''x''. If <math>x = \pi\,\!</math>, then | |||
| ===Imaginary exponents=== | |||
| {{main|Euler's formula}} | |||
| {{See also|Exponentiation#Complex_exponents_with_a_positive_real_base|l1=Complex exponents with a positive real base}} | |||
| ], with the final point being the actual value of {{math|(1 + {{sfrac|''iπ''|''N''}})<sup>''N''</sup>}}. It can be seen that as {{mvar|N}} gets larger {{math|(1 + {{sfrac|''iπ''|''N''}})<sup>''N''</sup>}} approaches a limit of −1.]] | |||
| Euler's identity asserts that <math>e^{i\pi}</math> is equal to −1. The expression <math>e^{i\pi}</math> is a special case of the expression <math>e^z</math>, where {{math|''z''}} is any ]. In general, <math>e^z</math> is defined for complex {{math|''z''}} by extending one of the ] from real exponents to complex exponents. For example, one common definition is: | |||
| : |
:<math>e^z = \lim_{n\to\infty} \left(1+\frac z n \right)^n.</math> | ||
| Euler's identity therefore states that the limit, as {{math|''n''}} approaches infinity, of <math>(1 + i\pi/n)^n</math> is equal to −1. This limit is illustrated in the animation to the right. | |||
| Since | |||
| ] | |||
| :<math>\cos \pi = -1 \, \! </math> | |||
| Euler's identity is a ] of ], which states that for any ] {{math|''x''}}, | |||
| : <math>e^{ix} = \cos x + i\sin x</math> | |||
| and | |||
| where the inputs of the ] sine and cosine are given in ]s. | |||
| :<math>\sin \pi = 0\,\!</math>, | |||
| In particular, when {{math|''x'' {{=}} ''π''}}, | |||
| : <math>e^{i \pi} = \cos \pi + i\sin \pi.</math> | |||
| Since | |||
| :<math>\cos \pi = -1</math> | |||
| and | |||
| :<math>\sin \pi = 0,</math> | |||
| it follows that | it follows that | ||
| : <math>e^{i \pi} = -1 |
: <math>e^{i \pi} = -1 + 0 i,</math> | ||
| which |
which yields Euler's identity: | ||
| : <math>e^{i \pi} +1 = 0.</math> | |||
| ==Perceptions of the identity== | |||
| Many people find this identity remarkable for its ]. The identity links what are arguably the most fundamental ]s: | |||
| ===Geometric interpretation=== | |||
| * The number 0. | |||
| Any complex number <math>z = x + iy</math> can be represented by the point <math>(x, y)</math> on the ]. This point can also be represented in ] as <math>(r, \theta)</math>, where ''r'' is the absolute value of ''z'' (distance from the origin), and <math>\theta</math> is the argument of ''z'' (angle counterclockwise from the positive ''x''-axis). By the definitions of sine and cosine, this point has cartesian coordinates of <math>(r \cos \theta, r \sin \theta)</math>, implying that <math>z = r(\cos \theta + i \sin \theta)</math>. According to Euler's formula, this is equivalent to saying <math>z = r e^{i\theta}</math>. | |||
| * The number 1. | |||
| * The number π is a fundamental constant of ], ], and ]. | |||
| * The number ''e'' is fundamental in the study of ]s and occurs widely in ]. | |||
| * The number ''i'', which together with the real numbers and arithmetic, generates the ]s (this leads to solutions for all nonconstant polynomials and deeper insights into many operators such as ]). | |||
| Euler's identity says that <math>-1 = e^{i\pi}</math>. Since <math>e^{i\pi}</math> is <math>r e^{i\theta}</math> for ''r'' = 1 and <math>\theta = \pi</math>, this can be interpreted as a fact about the number −1 on the complex plane: its distance from the origin is 1, and its angle from the positive ''x''-axis is <math>\pi</math> radians. | |||
| Furthermore, the most fundamental functions of ] are also present exactly once: ], ], and ]. As well, an equation with zero on one side is the most fundamental relation in mathematics. | |||
| Additionally, when any complex number ''z'' is ] by <math>e^{i\theta}</math>, it has the effect of rotating ''z'' counterclockwise by an angle of <math>\theta</math> on the complex plane. Since multiplication by −1 reflects a point across the origin, Euler's identity can be interpreted as saying that rotating any point <math>\pi</math> radians around the origin has the same effect as reflecting the point across the origin. Similarly, setting <math>\theta</math> equal to <math>2\pi</math> yields the related equation <math>e^{2\pi i} = 1,</math> which can be interpreted as saying that rotating any point by one ] around the origin returns it to its original position. | |||
| ], the noted ] ] and ] professor, after proving the identity in a lecture, said, "It is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth."{{rf|1|Maor}} | |||
| == |
==Generalizations== | ||
| Euler's identity is also a special case of the more general identity that the {{mvar|n}}th ], for {{math|''n'' > 1}}, add up to 0: | |||
| * Maor, Eli, ''e: The Story of a number'' (Princeton University Press, 1998), ISBN 0691058547 | |||
| :<math>\sum_{k=0}^{n-1} e^{2 \pi i \frac{k}{n}} = 0 .</math> | |||
| Euler's identity is the case where {{math|''n'' {{=}} 2}}. | |||
| A similar identity also applies to ]: let {{math|{{mset|''i'', ''j'', ''k''}}}} be the basis ]s; then, | |||
| :<math>e^{\frac{1}{\sqrt 3}(i \pm j \pm k)\pi} + 1 = 0. </math> | |||
| More generally, let {{mvar|q}} be a quaternion with a zero real part and a norm equal to {{math|1}}; that is, <math>q=ai+bj+ck,</math> with <math>a^2+b^2+c^2=1.</math> Then one has | |||
| :<math>e^{q\pi} + 1 = 0. </math> | |||
| The same formula applies to ]s, with a zero real part and a norm equal to {{math|1}}. These formulas are a direct generalization of Euler's identity, since <math>i</math> and <math>-i</math> are the only complex numbers with a zero real part and a norm (absolute value) equal to {{math|1}}. | |||
| ==History== | |||
| While Euler's identity is a direct result of ], published in his monumental work of mathematical analysis in 1748, '']'',<ref>Conway & Guy, p. 254–255.</ref> it is questionable whether the particular concept of linking five fundamental constants in a compact form can be attributed to Euler himself, as he may never have expressed it.<ref name=Sandifer2007>Sandifer, p. 4.</ref> | |||
| ] states the following.<ref>Wilson, p. 151-152.</ref> | |||
| {{quote|text= | |||
| We've seen how it can easily be deduced from results of ] and ], but that neither of them seem to have done so. Even Euler does not seem to have written it down explicitly – and certainly it doesn't appear in any of his publications – though he must surely have realized that it follows immediately from his identity ]], {{nowrap|''e<sup>ix</sup>'' {{=}} cos ''x'' + ''i'' sin ''x''}}. Moreover, it seems to be unknown who first stated the result explicitly.... | |||
| }} | |||
| == See also == | |||
| {{Portal|Mathematics}} | |||
| *] | |||
| *] | |||
| *] | |||
| ==Notes== | ==Notes== | ||
| {{reflist|group=note}} | |||
| {{ent|1|Maor}} Maor, p. 160. Maor cites Edward Kasner and James Newman's, ''Mathematics and the Imagination'' (New York: Simon and Schuster, 1940), pp. 103–104, as the source for this quote. | |||
| ==References== | |||
| {{Reflist|colwidth=20em}} | |||
| == |
===Sources=== | ||
| * ], and ] (1996), '''', Springer {{ISBN|978-0-387-97993-9}} | |||
| * ] | |||
| * ] (10 May 2004), "", '']'' | |||
| * ] (1999), ''Euler: The Master of Us All'', ] {{ISBN|978-0-88385-328-3}} | |||
| * Euler, Leonhard (1922), '''', Leipzig: B. G. Teubneri | |||
| * ], and ] (1940), '']'', ] | |||
| * ] (1998), ''{{mvar|e}}: The Story of a number'', ] {{ISBN|0-691-05854-7}} | |||
| * Nahin, Paul J. (2006), ''Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills'', ] {{ISBN|978-0-691-11822-2}} | |||
| * ] (1992), ''Beyond Numeracy: An Uncommon Dictionary of Mathematics'', ] {{ISBN|0-14-014574-5}} | |||
| * Reid, Constance (various editions), '']'', ] | |||
| * Sandifer, C. Edward (2007), '''', ] {{ISBN|978-0-88385-563-8}} | |||
| *{{citation |title= A Most Elegant Equation: Euler's formula and the beauty of mathematics |first= David |last= Stipp |year=2017 |publisher= ]}} | |||
| *{{cite journal | author-link= David G. Wells | last1 = Wells | first1 = David | year = 1990 | title = Are these the most beautiful? | journal = ] | volume = 12 | issue = 3| pages = 37–41 | doi = 10.1007/BF03024015 | s2cid = 121503263 }} | |||
| *{{citation |first= Robin |last= Wilson |author-link= Robin Wilson (mathematician) |title= Euler's Pioneering Equation: The most beautiful theorem in mathematics |publisher= ] |year= 2018 |isbn= 978-0-192-51406-6 }} | |||
| *{{Citation |last1= Zeki |first1= S. |last2= Romaya |first2= J. P. |last3= Benincasa |first3= D. M. T. |last4= Atiyah |first4= M. F. |author-link1= Semir Zeki |author-link4= Michael Atiyah |title= The experience of mathematical beauty and its neural correlates |journal= Frontiers in Human Neuroscience |volume= 8 |pages= 68 | year= 2014 |doi= 10.3389/fnhum.2014.00068|pmc= 3923150 |pmid=24592230|doi-access= free }} | |||
| ==External links== | ==External links== | ||
| {{Wikiquote|Euler's identity}} | |||
| * | |||
| * | |||
| {{Leonhard Euler}} | |||
| ] | |||
| {{DEFAULTSORT:Euler's identity}} | |||
| ] | |||
| ] | ] | ||
| ] | ] | ||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 10:34, 1 January 2025
Mathematical equation linking e, i and pi For other uses, see List of things named after Leonhard Euler § Identities.| Part of a series of articles on the |
| mathematical constant e |
|---|
 |
| Properties |
| Applications |
| Defining e |
| People |
| Related topics |
In mathematics, Euler's identity (also known as Euler's equation) is the equality where
- is Euler's number, the base of natural logarithms,
- is the imaginary unit, which by definition satisfies , and
- is pi, the ratio of the circumference of a circle to its diameter.
Euler's identity is named after the Swiss mathematician Leonhard Euler. It is a special case of Euler's formula when evaluated for . Euler's identity is considered to be an exemplar of mathematical beauty as it shows a profound connection between the most fundamental numbers in mathematics. In addition, it is directly used in a proof that π is transcendental, which implies the impossibility of squaring the circle.
Mathematical beauty
Euler's identity is often cited as an example of deep mathematical beauty. Three of the basic arithmetic operations occur exactly once each: addition, multiplication, and exponentiation. The identity also links five fundamental mathematical constants:
- The number 0, the additive identity
- The number 1, the multiplicative identity
- The number π (π = 3.14159...), the fundamental circle constant
- The number e (e = 2.71828...), also known as Euler's number, which occurs widely in mathematical analysis
- The number i, the imaginary unit such that
The equation is often given in the form of an expression set equal to zero, which is common practice in several areas of mathematics.
Stanford University mathematics professor Keith Devlin has said, "like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler's equation reaches down into the very depths of existence". And Paul Nahin, a professor emeritus at the University of New Hampshire, who has written a book dedicated to Euler's formula and its applications in Fourier analysis, describes Euler's identity as being "of exquisite beauty".
Mathematics writer Constance Reid has opined that Euler's identity is "the most famous formula in all mathematics". And Benjamin Peirce, a 19th-century American philosopher, mathematician, and professor at Harvard University, after proving Euler's identity during a lecture, stated that the identity "is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth".
A poll of readers conducted by The Mathematical Intelligencer in 1990 named Euler's identity as the "most beautiful theorem in mathematics". In another poll of readers that was conducted by Physics World in 2004, Euler's identity tied with Maxwell's equations (of electromagnetism) as the "greatest equation ever".
At least three books in popular mathematics have been published about Euler's identity:
- Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills, by Paul Nahin (2011)
- A Most Elegant Equation: Euler's formula and the beauty of mathematics, by David Stipp (2017)
- Euler's Pioneering Equation: The most beautiful theorem in mathematics, by Robin Wilson (2018).
Explanations
Imaginary exponents
Main article: Euler's formula See also: Complex exponents with a positive real base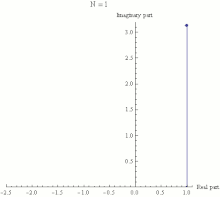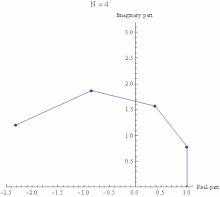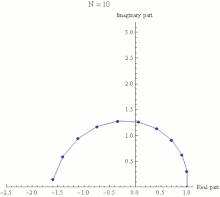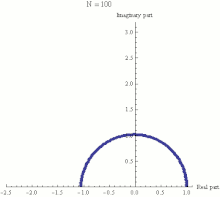
Euler's identity asserts that is equal to −1. The expression is a special case of the expression , where z is any complex number. In general, is defined for complex z by extending one of the definitions of the exponential function from real exponents to complex exponents. For example, one common definition is:
Euler's identity therefore states that the limit, as n approaches infinity, of is equal to −1. This limit is illustrated in the animation to the right.

Euler's identity is a special case of Euler's formula, which states that for any real number x,
where the inputs of the trigonometric functions sine and cosine are given in radians.
In particular, when x = π,
Since
and
it follows that
which yields Euler's identity:
Geometric interpretation
Any complex number can be represented by the point on the complex plane. This point can also be represented in polar coordinates as , where r is the absolute value of z (distance from the origin), and is the argument of z (angle counterclockwise from the positive x-axis). By the definitions of sine and cosine, this point has cartesian coordinates of , implying that . According to Euler's formula, this is equivalent to saying .
Euler's identity says that . Since is for r = 1 and , this can be interpreted as a fact about the number −1 on the complex plane: its distance from the origin is 1, and its angle from the positive x-axis is radians.
Additionally, when any complex number z is multiplied by , it has the effect of rotating z counterclockwise by an angle of on the complex plane. Since multiplication by −1 reflects a point across the origin, Euler's identity can be interpreted as saying that rotating any point radians around the origin has the same effect as reflecting the point across the origin. Similarly, setting equal to yields the related equation which can be interpreted as saying that rotating any point by one turn around the origin returns it to its original position.
Generalizations
Euler's identity is also a special case of the more general identity that the nth roots of unity, for n > 1, add up to 0:
Euler's identity is the case where n = 2.
A similar identity also applies to quaternion exponential: let {i, j, k} be the basis quaternions; then,
More generally, let q be a quaternion with a zero real part and a norm equal to 1; that is, with Then one has
The same formula applies to octonions, with a zero real part and a norm equal to 1. These formulas are a direct generalization of Euler's identity, since and are the only complex numbers with a zero real part and a norm (absolute value) equal to 1.
History
While Euler's identity is a direct result of Euler's formula, published in his monumental work of mathematical analysis in 1748, Introductio in analysin infinitorum, it is questionable whether the particular concept of linking five fundamental constants in a compact form can be attributed to Euler himself, as he may never have expressed it.
Robin Wilson states the following.
We've seen how it can easily be deduced from results of Johann Bernoulli and Roger Cotes, but that neither of them seem to have done so. Even Euler does not seem to have written it down explicitly – and certainly it doesn't appear in any of his publications – though he must surely have realized that it follows immediately from his identity , e = cos x + i sin x. Moreover, it seems to be unknown who first stated the result explicitly....
See also
Notes
- The term "Euler's identity" (or "Euler identity") is also used elsewhere to refer to other concepts, including the related general formula e = cos x + i sin x, and the Euler product formula. See also List of things named after Leonhard Euler.
References
- Dunham, 1999, p. xxiv.
- Stepanov, S.A. (2001) , "Euler identity", Encyclopedia of Mathematics, EMS Press
- Milla, Lorenz (2020), The Transcendence of π and the Squaring of the Circle, arXiv:2003.14035
- Hines, Robert. "e is transcendental" (PDF). University of Colorado. Archived (PDF) from the original on 2021-06-23.
- Gallagher, James (13 February 2014). "Mathematics: Why the brain sees maths as beauty". BBC News Online. Retrieved 26 December 2017.
- Paulos, 1992, p. 117.
- Nahin, 2006, p. 1.
- Nahin, 2006, p. xxxii.
- Reid, chapter e.
- Maor, p. 160, and Kasner & Newman, p. 103–104.
- Wells, 1990.
- Crease, 2004.
- Nahin, Paul (2011). Dr. Euler's fabulous formula : cures many mathematical ills. Princeton University Press. ISBN 978-0-691-11822-2.
- Stipp, David (2017). A Most Elegant Equation : Euler's Formula and the Beauty of Mathematics (First ed.). Basic Books. ISBN 978-0-465-09377-9.
- Wilson, Robin (2018). Euler's pioneering equation : the most beautiful theorem in mathematics. Oxford: Oxford University Press. ISBN 978-0-19-879493-6.
- Conway & Guy, p. 254–255.
- Sandifer, p. 4.
- Wilson, p. 151-152.
Sources
- Conway, John H., and Guy, Richard K. (1996), The Book of Numbers, Springer ISBN 978-0-387-97993-9
- Crease, Robert P. (10 May 2004), "The greatest equations ever", Physics World
- Dunham, William (1999), Euler: The Master of Us All, Mathematical Association of America ISBN 978-0-88385-328-3
- Euler, Leonhard (1922), Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus, Leipzig: B. G. Teubneri
- Kasner, E., and Newman, J. (1940), Mathematics and the Imagination, Simon & Schuster
- Maor, Eli (1998), e: The Story of a number, Princeton University Press ISBN 0-691-05854-7
- Nahin, Paul J. (2006), Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills, Princeton University Press ISBN 978-0-691-11822-2
- Paulos, John Allen (1992), Beyond Numeracy: An Uncommon Dictionary of Mathematics, Penguin Books ISBN 0-14-014574-5
- Reid, Constance (various editions), From Zero to Infinity, Mathematical Association of America
- Sandifer, C. Edward (2007), Euler's Greatest Hits, Mathematical Association of America ISBN 978-0-88385-563-8
- Stipp, David (2017), A Most Elegant Equation: Euler's formula and the beauty of mathematics, Basic Books
- Wells, David (1990). "Are these the most beautiful?". The Mathematical Intelligencer. 12 (3): 37–41. doi:10.1007/BF03024015. S2CID 121503263.
- Wilson, Robin (2018), Euler's Pioneering Equation: The most beautiful theorem in mathematics, Oxford University Press, ISBN 978-0-192-51406-6
- Zeki, S.; Romaya, J. P.; Benincasa, D. M. T.; Atiyah, M. F. (2014), "The experience of mathematical beauty and its neural correlates", Frontiers in Human Neuroscience, 8: 68, doi:10.3389/fnhum.2014.00068, PMC 3923150, PMID 24592230
 where
where
 is
is  is the
is the  , and
, and is
is  when evaluated for
when evaluated for  . Euler's identity is considered to be an exemplar of
. Euler's identity is considered to be an exemplar of  is equal to −1. The expression
is equal to −1. The expression  , where z is any
, where z is any 
 is equal to −1. This limit is illustrated in the animation to the right.
is equal to −1. This limit is illustrated in the animation to the right.





 can be represented by the point
can be represented by the point  on the
on the  , where r is the absolute value of z (distance from the origin), and
, where r is the absolute value of z (distance from the origin), and  is the argument of z (angle counterclockwise from the positive x-axis). By the definitions of sine and cosine, this point has cartesian coordinates of
is the argument of z (angle counterclockwise from the positive x-axis). By the definitions of sine and cosine, this point has cartesian coordinates of  , implying that
, implying that  . According to Euler's formula, this is equivalent to saying
. According to Euler's formula, this is equivalent to saying  .
.
 . Since
. Since  for r = 1 and
for r = 1 and  , this can be interpreted as a fact about the number −1 on the complex plane: its distance from the origin is 1, and its angle from the positive x-axis is
, this can be interpreted as a fact about the number −1 on the complex plane: its distance from the origin is 1, and its angle from the positive x-axis is  , it has the effect of rotating z counterclockwise by an angle of
, it has the effect of rotating z counterclockwise by an angle of  yields the related equation
yields the related equation  which can be interpreted as saying that rotating any point by one
which can be interpreted as saying that rotating any point by one 

 with
with  Then one has
Then one has

 are the only complex numbers with a zero real part and a norm (absolute value) equal to 1.
are the only complex numbers with a zero real part and a norm (absolute value) equal to 1.