| Revision as of 04:02, 14 October 2011 editPatrick0Moran (talk | contribs)Extended confirmed users12,602 edits Undid revision 455479625 by 91.122.1.39 (talk)← Previous edit | Latest revision as of 03:52, 20 December 2024 edit undoStickynotememo (talk | contribs)7 editsm See also Hashgraph with symbol H-bar | ||
| Line 1: | Line 1: | ||
| {{Short description|Physical constant in quantum mechanics}} | |||
| {{pp-move-indef}} | |||
| {{For|the law governing black-body radiation|Planck's law}} | |||
| {| class="wikitable" style="float:right; margin:0em 1em 1em 1em" | |||
| {{Infobox physical quantity | |||
| ! Values of ''h'' | |||
| | name = Planck constant | |||
| ! Units | |||
| | unit = joule per hertz (joule second) | |||
| |- | |||
| | otherunits = electronvolt per hertz (electronvolt second) | |||
| | {{val|6.62606957|(29)|e=-34}} || ]·]<ref name="2010 CODATA">P.J. Mohr, B.N. Taylor, and D.B. Newell (2011), "The 2010 CODATA Recommended Values of the Fundamental Physical Constants" (Web Version 6.0). This database was developed by J. Baker, M. Douma, and S. Kotochigova. Available: http://physics.nist.gov/constants . National Institute of Standards and Technology, Gaithersburg, MD 20899.</ref> | |||
| | symbols = <math>h</math> | |||
| |- | |||
| | baseunits =]⋅]{{sup|2}}⋅]{{sup|−1}} <!-- energy per cycle or energy times second is (kg (m^2)/(s^2)) s, so s is -1.--> | |||
| | {{val|4.135667516|(91)|e=-15}} || ]·]<ref name="2010 CODATA" /> | |||
| | dimension = <math>\mathsf{M} \mathsf{L}^{2} \mathsf{T}^{-1}</math> | |||
| |- | |||
| | derivations = | |||
| | {{val|6.62606957|(29)|e=-27}} || ]·]<ref name="2010 CODATA" /><!--]--> | |||
| | value = {{physconst|h|ref=no}}{{br}}{{physconst|h_eV/Hz|ref=no}} | |||
| |- | |||
| }} | |||
| ! Values of ''ħ'' | |||
| {{Infobox physical quantity | |||
| ! Units | |||
| | name = Reduced Planck constant | |||
| |- | |||
| | unit = joule-second | |||
| | {{val|1.054571726|(47)|e=-34}} || ]·]<ref name="2010 CODATA" /> | |||
| | otherunits = electronvolt-second | |||
| |- | |||
| | symbols = <math>\hbar</math> | |||
| | {{val|6.58211928|(15)|e=-16}} || ]·]<ref name="2010 CODATA" /> | |||
| | baseunits =]⋅]{{sup|2}}⋅]{{sup|−1}} | |||
| |- | |||
| | dimension = <math>\mathsf{M} \mathsf{L}^{2} \mathsf{T}^{-1}</math> | |||
| | {{val|1.054571726|(47)|e=-27}} || ]·]<ref name="2010 CODATA" /><!--]--> | |||
| | derivations = | |||
| |} | |||
| {{ublist | |||
| <small>]</small> | |||
| | <math>\hbar = h/(2 \pi)</math> | |||
| }} | |||
| | value = {{physconst|hbar|ref=no}}{{br}}{{physconst|hbar_eVs|ref=no}} | |||
| }} | |||
| The '''Planck constant''', or '''Planck's constant''', denoted by {{nowrap|<math display=inline>h</math>,}}<ref name="NIST h">{{Cite web |date=20 May 2019 |title=Planck constant |url=https://physics.nist.gov/cgi-bin/cuu/Value?h |url-status=live |archive-url=https://web.archive.org/web/20220527011505/https://physics.nist.gov/cgi-bin/cuu/Value?h |archive-date=2022-05-27 |access-date=2023-09-03 |website=The NIST Reference on Constants, Units, and Uncertainty |publisher=]}}</ref> is a fundamental ]<ref name="NIST h" /> of foundational importance in ]: a ]'s energy is equal to its ] multiplied by the Planck constant, and the ] of a ] equals the Planck constant divided by the associated particle momentum. The closely related '''reduced Planck constant''', equal to <math display="inline">h/(2\pi)</math> and denoted <math display="inline">\hbar</math> is commonly used in quantum physics equations. | |||
| The '''Planck constant''' (denoted '''''h'''''), also called '''Planck's constant''', is a ] reflecting the sizes of energy ] in ]. It is named after ], one of the founders of ], who discovered it in 1899. Classical ] requires the existence of h (but does not define its value).<ref>{{Citation|title=Statistical mechanics: an intermediate course | |||
| |author= Giuseppe Morandi, F. Napoli, E. Ercolessi|quote=See page 85|url=http://books.google.com/?id=MhInFlnNsREC&pg=PA51&lpg=PA51&dq=celestial+mechanics+planck+constant#v=onepage&q=celestial%20mechanics%20planck%20constant&f=false|isbn=9789810244774|year=2001}}</ref> | |||
| The constant was postulated by ] in 1900 as a ] needed to explain experimental ] radiation.<ref name="Planck01" /> Planck later referred to the constant as the "quantum of ]".<ref>{{Cite web |title=Max Planck Nobel Lecture |url=https://www.nobelprize.org/prizes/physics/1918/planck/lecture/ |url-status=live |archive-url=https://web.archive.org/web/20230714164215/https://www.nobelprize.org/prizes/physics/1918/planck/lecture/ |archive-date=2023-07-14 |access-date=2023-07-14}}</ref> In 1905, ] associated the "quantum" or minimal element of the energy to the electromagnetic wave itself. Max Planck received the 1918 ] "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta". | |||
| The Planck constant was first described as the ] between the ] (''E'') of a ] and the ] of its associated ] (''ν''). This relation between the energy and frequency is called the '''Planck relation''' or the '''Planck–Einstein equation''': | |||
| In ], the Planck constant is used, together with other constants, to define the ], the ] of mass.<ref>{{SIbrochure9th|page=131}}</ref> The SI units are defined in such a way that, when the Planck constant is expressed in SI units, it has the exact value {{nowrap|<math>h</math> {{=}} {{physconst|h|after=.}}}}<ref>{{cite web |date=2018-11-16 |title=Resolutions of the 26th CGPM |url=https://www.bipm.org/utils/common/pdf/CGPM-2018/26th-CGPM-Resolutions.pdf |url-status=dead |archive-url=https://web.archive.org/web/20181119214326/https://www.bipm.org/utils/common/pdf/CGPM-2018/26th-CGPM-Resolutions.pdf |archive-date=2018-11-19 |access-date=2018-11-20 |website=BIPM |language=en-GB}}</ref> | |||
| :<math>E = h\nu.\,</math> | |||
| == History == | |||
| Since the ] ''<math>\nu</math>'', ] ''λ'', and ] ''c'' are related by {{nowrap|''λν'' {{=}} ''c''}}, the Planck relation can also be expressed as | |||
| === Origin of the constant === | |||
| {{Main|Planck's law}} | |||
| :<math>E = \frac{hc}{\lambda}.\,</math> | |||
| ]: "In this edifice taught Max Planck, the discoverer of the elementary quantum of action ''h'', from 1889 to 1928."]] | |||
| ]. Each curve represents behavior at different body temperatures. The Planck constant ''h'' is used to explain the shape of these curves.]] | |||
| Planck's constant was formulated as part of Max Planck's successful effort to produce a mathematical expression that accurately predicted the observed spectral distribution of thermal radiation from a closed furnace (]).<ref name="Bitter">{{Cite book |last1=Bitter |first1=Francis |title=Fields and particles |last2=Medicus |first2=Heinrich A. |date=1973 |publisher=Elsevier |location=New York |pages=137–144 |author-link=Francis Bitter}}</ref> This mathematical expression is now known as Planck's law. | |||
| In the last years of the 19th century, Max Planck was investigating the problem of black-body radiation first posed by ] some 40 years earlier. Every ] spontaneously and continuously emits ]. There was no expression or explanation for the overall shape of the observed emission spectrum. At the time, ] fit the data for short wavelengths and high temperatures, but failed for long wavelengths.<ref name="Bitter" />{{rp|141}} Also around this time, but unknown to Planck, ] had derived theoretically a formula, now known as the ], that could reasonably predict long wavelengths but failed dramatically at short wavelengths. | |||
| In 1923, ] generalized this relation by postulating that the Planck constant represents the proportionality between the momentum and the quantum wavelength of not just the photon, but any particle. This was confirmed by experiments soon afterwards. | |||
| Approaching this problem, Planck hypothesized that the equations of motion for light describe a set of ]s, one for each possible frequency. He examined how the ] of the oscillators varied with the temperature of the body, trying to match Wien's law, and was able to derive an approximate mathematical function for the black-body spectrum,<ref name="Planck01">{{citation | first = Max | last = Planck | author-link = Max Planck | title = Ueber das Gesetz der Energieverteilung im Normalspectrum |language=de | url = http://www.physik.uni-augsburg.de/annalen/history/historic-papers/1901_309_553-563.pdf | journal = ] | year = 1901 | volume = 309 | issue = 3 | pages = 553–63 | doi = 10.1002/andp.19013090310 | bibcode = 1901AnP...309..553P | doi-access = free | access-date = 2008-12-15 | archive-date = 2012-06-10 | archive-url = https://web.archive.org/web/20120610124128/http://www.physik.uni-augsburg.de/annalen/history/historic-papers/1901_309_553-563.pdf | url-status = live }}. English translations: | |||
| Planck discovered that physical ] could not take on any indiscriminate value. Instead, the action must be some multiple of a very small quantity (later to be named the "] of action" and now called Planck's constant). This inherent granularity is counterintuitive in the everyday world, where it is possible to "make things a little bit hotter" or "move things a little bit faster". This is because the quanta of action are very, very small in comparison to everyday human experience. Thus, on the macro scale quantum mechanics and classical physics converge. Nevertheless, it is impossible, as Planck found out, to explain some phenomena without accepting that action is quantized. In many cases, such as for monochromatic light or for atoms, the quantum of action also implies that only certain energy levels are allowed, and values in between are forbidden. | |||
| *{{Cite web |title=On the Law of Distribution of Energy in the Normal Spectrum |url=http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Planck-1901/Planck-1901.html |url-status=dead |archive-url=https://web.archive.org/web/20080418002757/http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Planck-1901/Planck-1901.html |archive-date=2008-04-18}} | |||
| *{{cite web |url=http://theochem.kuchem.kyoto-u.ac.jp/Ando/planck1901.pdf |title=On the Law of Distribution of Energy in the Normal Spectrum |access-date=2011-10-13 |url-status=dead |archive-url=https://web.archive.org/web/20111006162543/http://theochem.kuchem.kyoto-u.ac.jp/Ando/planck1901.pdf |archive-date=2011-10-06 }}</ref> which gave a simple empirical formula for long wavelengths. | |||
| Planck tried to find a mathematical expression that could reproduce Wien's law (for short wavelengths) and the empirical formula (for long wavelengths). This expression included a constant, <math>h</math>, which is thought to be for {{lang|de|Hilfsgröße}} (auxiliary quantity),<ref>{{Cite arXiv |eprint=physics/0402064v1 |first=Luis J. |last=Boya |title=The Thermal Radiation Formula of Planck (1900) |date=2004}}</ref> and subsequently became known as the Planck constant. The expression formulated by Planck showed that the spectral radiance per unit frequency of a body for ] {{math|''ν''}} at ] {{math|''T''}} is given by | |||
| Closely related to the Planck constant is the '''reduced Planck constant''', sometimes called the '''Dirac constant''' after ]. It is equal to the Planck constant divided by 2], and is denoted ''ħ'' ("'''h-bar'''"): | |||
| :<math>\hbar = \frac{h}{2 \pi}.</math> | |||
| <math display="block">B_\nu(\nu, T) d\nu= \frac{ 2 h \nu^3}{c^2} \frac{1}{e^\frac{h\nu}{k_\mathrm B T} - 1}d\nu ,</math> | |||
| The reduced Planck constant is used when frequency is expressed in terms of ]s per second ("]") instead of ]. The energy of a photon with angular frequency ''ω'', where ''ω'' = 2π''ν'', is given by | |||
| :<math>E = \hbar \omega.</math> | |||
| where <math>k_\text{B}</math> is the ], <math>h</math> is the Planck constant, and <math>c</math> is the ] in the medium, whether material or vacuum.<ref name="Planck 1914 6 168">{{Cite book |last=Planck |first=M. |url=https://archive.org/details/theoryofheatradi00planrich |title=The Theory of Heat Radiation |publisher=P. Blakiston's Son |translator-last=Masius |translator-first=M. |year=1914 |edition=2nd |pages=6, 168 |ol=7154661M |author-link=Max Planck}}</ref><ref name="Chan8">{{cite book |last=Chandrasekhar |first=S. |url=https://archive.org/details/radiativetransfe0000chan |title=Radiative Transfer |publisher=] |year=1960 |isbn=978-0-486-60590-6 |edition=revised reprint |page=8 |author-link=Subrahmanyan Chandrasekhar |url-access=registration |orig-year=1950}}</ref><ref name="Rybicki 1979 22">{{cite book |last1=Rybicki |first1=G. B. |url=https://books.google.com/books?id=LtdEjNABMlsC |title=Radiative Processes in Astrophysics |last2=Lightman |first2=A. P. |publisher=] |year=1979 |isbn=978-0-471-82759-7 |page=22 |author-link2=Alan Lightman |access-date=2020-05-20 |archive-url=https://web.archive.org/web/20200727111701/https://books.google.com/books?id=LtdEjNABMlsC |archive-date=2020-07-27 |url-status=live}}</ref> | |||
| ==Value== | |||
| The Planck constant has ]s of physical ]; these are the same as those of ], i.e., ] multiplied by ] or ] multiplied by ]. In ], the Planck constant is expressed in ]s ({{nowrap|J·s}}) or ({{nowrap|]·]·]}}). | |||
| Planck soon realized that his solution was not unique. There were several different solutions, each of which gave a different value for the entropy of the oscillators.<ref name="Planck01" /> To save his theory, Planck resorted to using the then-controversial theory of ],<ref name="Planck01" /> which he described as "an act of desperation".<ref name="Kragh">{{Citation |last=Kragh |first=Helge |title=Max Planck: the reluctant revolutionary |date=1 December 2000 |url=https://physicsworld.com/a/max-planck-the-reluctant-revolutionary/ |archive-url=https://web.archive.org/web/20090108204645/http://physicsworld.com/cws/article/print/373 |publisher=PhysicsWorld.com |archive-date=2009-01-08 |author-link=Helge Kragh}}</ref> One of his new boundary conditions was | |||
| The value of the Planck constant is:<ref name="2010 CODATA" /> | |||
| :<math>h = 6.626\ 069\ 57(29)\times 10^{-34}\ \mathrm{J \cdot s} = 4.135\ 667\ 516(91)\times 10^{-15}\ \mathrm{eV \cdot s}.</math> | |||
| The value of the reduced Planck constant is: | |||
| :<math>\hbar = {{h}\over{2\pi}} = 1.054\ 571\ 726(47)\times 10^{-34}\ \mathrm{J \cdot s} = 6.582\ 119\ 28(15)\times 10^{-16}\ \mathrm{eV \cdot s}.</math> | |||
| The two digits between the parentheses denote the ] in the last two digits of the value. The figures cited here are the 2010 ] recommended values for the constants and their uncertainties. The 2010 CODATA results were made available in June 2011<ref>{{cite web|url=http://physics.nist.gov/cuu/Reference/versioncon.shtml|title=CODATA recommended values}}</ref> and represent the best-known, internationally-accepted values for these constants, based on all data available as of 2010. New CODATA figures are scheduled to be published approximately every four years. | |||
| {{blockquote|text=to interpret ''U''<sub>''N''</sub> not as a continuous, infinitely divisible quantity, but as a discrete quantity composed of an integral number of finite equal parts. Let us call each such part the energy element ''ε'';|sign=Planck|source="On the Law of Distribution of Energy in the Normal Spectrum"<ref name="Planck01" />}} | |||
| ==Significance of the value== | |||
| With this new condition, Planck had imposed the quantization of the energy of the oscillators, in his own words, "a purely formal assumption ... actually I did not think much about it",<ref>{{Citation |last=Kragh |first=Helge |title=Quantum Generations: A History of Physics in the Twentieth Century |url=https://books.google.com/books?id=ELrFDIldlawC |page=62 |year=1999 |access-date=2021-10-31 |archive-url=https://web.archive.org/web/20211206180414/https://books.google.com/books?id=ELrFDIldlawC |url-status=live |publisher=Princeton University Press |isbn=978-0-691-09552-3 |archive-date=2021-12-06}}</ref> but one that would revolutionize physics. Applying this new approach to Wien's displacement law showed that the "energy element" must be proportional to the frequency of the oscillator, the first version of what is now sometimes termed the "]": | |||
| <math display="block">E = hf.</math> | |||
| The numerical value of the Planck constant depends entirely on the system of units used to measure it. When it is expressed in SI units, it is one of the smallest constants used in physics. This reflects the fact that, ''on a scale adapted to humans'', where energies are typically of the order of kilojoules and times are typically of the order of seconds or minutes, Planck's constant, the quantum of action, is very small. | |||
| Planck was able to calculate the value of <math>h</math> from experimental data on black-body radiation: his result, {{val|6.55|e=-34|u=J.s}}, is within 1.2% of the currently defined value.<ref name="Planck01" /> He also made the first determination of the ] <math>k_\text{B}</math> from the same data and theory.<ref name="PlanckNobel">{{Citation |last=Planck |first=Max |title=The Genesis and Present State of Development of the Quantum Theory (Nobel Lecture) |date=2 June 1920 |url=http://nobelprize.org/nobel_prizes/physics/laureates/1918/planck-lecture.html |access-date=13 December 2008 |archive-url=https://web.archive.org/web/20110715190331/http://nobelprize.org/nobel_prizes/physics/laureates/1918/planck-lecture.html |url-status=live |archive-date=15 July 2011 |author-link=Max Planck}}</ref> | |||
| Equivalently, the smallness of Planck's constant reflects the fact that everyday objects and systems are made of ''large'' number of particles. To take one example, green light of a ] of 555 ]s (approximately the wavelength to which human eyes are most sensitive) has a frequency of 540 THz (540{{e|12}} ]). Each ] has an energy ''E'' of ''hν'' = 3.58{{e|−19}} J. That is a very small energy in terms of everyday experience, but then everyday experience doesn't deal with individual photons any more than it deals with individual atoms or molecules. An amount of light that is compatible with everyday experience | |||
| is the energy of one ] of photons; its energy can be calculated by multiplying the photon energy by the ], ''N''<sub>A</sub> ≈ {{nowrap|6.022{{e|23}} mol<sup>−1</sup>}}. The result is that green light of wavelength 555 nm has an energy of 216 kJ/mol, a typical energy of everyday life. | |||
| <!-- | |||
| This energy is comparable in strength to some of the weaker ] such as with ], while that of ultraviolet light at 254 nm from a ] is a stronger 472 kJ/mol suiting it to the ] action of ]. | |||
| --> | |||
| <!-- | |||
| When the reduced Planck constant is treated as a conversion factor between ], in radians, and ], in joule-seconds (as seen in the ]), it may be written with units J·s/rad. | |||
| --> | |||
| ] | |||
| The Planck constant is related to the quantization of light and matter. Therefore, the Planck constant can be seen as an atomic-scale constant. In a unit system adapted to atomic scales, the ] is the appropriate unit of energy and the Petahertz the appropriate unit of frequency. In such an ] system, Planck's constant is indeed described by a number of order 1. | |||
| === Development and application === | |||
| ==Origins== | |||
| The black-body problem was revisited in 1905, when ] and ] (together) and ] independently proved that classical electromagnetism could ''never'' account for the observed spectrum. These proofs are commonly known as the "]", a name coined by ] in 1911. They contributed greatly (along with Einstein's work on the ]) in convincing physicists that Planck's postulate of quantized energy levels was more than a mere mathematical formalism. The first ] in 1911 was devoted to "the theory of radiation and quanta".<ref>{{Citation |title=Previous Solvay Conferences on Physics |url=http://www.solvayinstitutes.be/Conseils%20Solvay/PreviousPhysics.html |access-date=12 December 2008 |archive-url=https://web.archive.org/web/20081216120021/http://www.solvayinstitutes.be/Conseils%20Solvay/PreviousPhysics.html |url-status=dead |publisher=International Solvay Institutes |archive-date=16 December 2008}}</ref> | |||
| ===Black-body radiation=== | |||
| {{Main|Planck's law}} | |||
| ] at any given frequency. Each color is a different temperature. Planck was the first to explain the shape of these curves.]] | |||
| In the last years of the nineteenth century, Planck was investigating the problem of ] first posed by ] some forty years earlier. It is well known that hot objects glow, and that hotter objects glow brighter than cooler ones. The reason is that the electromagnetic field obeys laws of motion just like a mass on a spring, and can come to thermal equilibrium with hot atoms. When a hot object is in equilibrium with light, the amount of light it absorbs is equal to the amount of light it emits. If the object is black, meaning it absorbs all the light that hits it, then it emits the maximum amount of thermal light too. | |||
| ==== Photoelectric effect ==== | |||
| The assumption that blackbody radiation is thermal leads to an accurate prediction: the total amount of emitted energy goes up with the temperature according to a definite rule, the ] (1879–84). But it was also known that the colour of the light given off by a hot object changes with the temperature, so that "white hot" is hotter than "red hot". Nevertheless, ] discovered the mathematical relationship between the peaks of the curves at different temperatures, by using the principle of ]. At each different temperature, the curve is moved over by ] (1893). Wien also proposed an ] for the spectrum of the object, which was correct at high frequencies (short wavelength) but not at low frequencies (long wavelength).<ref name="bowleysanchez1999" >{{citation | |||
| {{Main|Photoelectric effect}} | |||
| | author=R. Bowley, M. Sánchez | |||
| The photoelectric effect is the emission of electrons (called "photoelectrons") from a surface when light is shone on it. It was first observed by ] in 1839, although credit is usually reserved for ],<ref name="Nobel21">See, e.g., {{cite web |last=Arrhenius |first=Svante |title=Presentation speech of the 1921 Nobel Prize for Physics |date=10 December 1922 |url=http://nobelprize.org/nobel_prizes/physics/laureates/1921/press.html |access-date=13 December 2008 |archive-url=https://web.archive.org/web/20110904232203/http://www.nobelprize.org/nobel_prizes/physics/laureates/1921/press.html |url-status=live |archive-date=4 September 2011 |author-link=Svante Arrhenius}}</ref> who published the first thorough investigation in 1887. Another particularly thorough investigation was published by ] (Lénárd Fülöp) in 1902.<ref name="Lenard">{{cite journal |last=Lenard |first=P. |title=Ueber die lichtelektrische Wirkung |url=https://zenodo.org/record/1424009 |journal=] |volume=313 |issue=5 |pages=149–198 |year=1902 |access-date=2019-07-03 |archive-url=https://web.archive.org/web/20190818204108/https://zenodo.org/record/1424009 |url-status=live |bibcode=1902AnP...313..149L |doi=10.1002/andp.19023130510 |archive-date=2019-08-18 |author-link=Philipp Lenard}}</ref> Einstein's 1905 paper<ref>{{cite journal |last=Einstein |first=Albert |title=Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt |url=http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1905_17_132-148.pdf |journal=] |volume=17 |issue=6 |pages=132–48 |year=1905 |access-date=2009-12-03 |archive-url=https://web.archive.org/web/20110709180735/http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1905_17_132-148.pdf |url-status=live |bibcode=1905AnP...322..132E |doi=10.1002/andp.19053220607 |archive-date=2011-07-09 |author-link=Albert Einstein |doi-access=free}}</ref> discussing the effect in terms of light quanta would earn him the Nobel Prize in 1921,<ref name="Nobel21" /> after his predictions had been confirmed by the experimental work of ].<ref name="Millikan">{{cite journal |last=Millikan |first=R. A. |title=A Direct Photoelectric Determination of Planck's '''h''' |journal=] |volume=7 |issue=3 |pages=355–88 |year=1916 |bibcode=1916PhRv....7..355M |doi=10.1103/PhysRev.7.355 |author-link=Robert Andrews Millikan |doi-access=free}}</ref> The Nobel committee awarded the prize for his work on the photo-electric effect, rather than relativity, both because of a bias against purely theoretical physics not grounded in discovery or experiment, and dissent amongst its members as to the actual proof that relativity was real.<ref>{{cite book |last=Isaacson |first=Walter |title=Einstein: His Life and Universe |date=2007-04-10 |publisher=Simon and Schuster |url=https://books.google.com/books?id=cdxWNE7NY6QC |access-date=2021-10-31 |archive-url=https://web.archive.org/web/20200109170326/https://books.google.com/books?id=cdxWNE7NY6QC |url-status=live |isbn=978-1-4165-3932-2 |archive-date=2020-01-09 |pages=309–314}}</ref><ref>{{Cite web |title=The Nobel Prize in Physics 1921 |url=https://www.nobelprize.org/nobel_prizes/physics/laureates/1921/ |url-status=live |archive-url=https://web.archive.org/web/20180703190346/https://www.nobelprize.org/nobel_prizes/physics/laureates/1921/ |archive-date=2018-07-03 |access-date=2014-04-23 |publisher=Nobel Foundation}}</ref> | |||
| | year=1999 | |||
| | title=Introductory Statistical Mechanics | |||
| | edition=2nd | |||
| | publisher=Clarendon Press | |||
| | location=Oxford | |||
| | isbn=0-19-850576-0}}</ref> It still wasn't clear ''why'' the spectrum of a hot object had the form that it has (see diagram). | |||
| Before Einstein's paper, electromagnetic radiation such as visible light was considered to behave as a wave: hence the use of the terms "frequency" and "wavelength" to characterize different types of radiation. The energy transferred by a wave in a given time is called its ]. The light from a theatre spotlight is more ''intense'' than the light from a domestic lightbulb; that is to say that the spotlight gives out more energy per unit time and per unit space (and hence consumes more electricity) than the ordinary bulb, even though the color of the light might be very similar. Other waves, such as sound or the waves crashing against a seafront, also have their intensity. However, the energy account of the photoelectric effect did not seem to agree with the wave description of light. | |||
| Planck hypothesized that the equations of motion for light are a set of ]s, one for each possible frequency. He examined how the ] of the oscillators varied with the temperature of the body, trying to match Wien's law, and was able to derive an approximate mathematical function for black-body spectrum.<ref name="Planck01">{{citation | first = Max | last = Planck | author-link = Max Planck | title = Ueber das Gesetz der Energieverteilung im Normalspectrum | url = http://www.physik.uni-augsburg.de/annalen/history/historic-papers/1901_309_553-563.pdf | journal = ] | year = 1901 | volume = 309 | issue = 3 | pages = 553–63 | doi = 10.1002/andp.19013090310|bibcode = 1901AnP...309..553P }}. English translation: "".</ref> | |||
| The "photoelectrons" emitted as a result of the photoelectric effect have a certain ], which can be measured. This kinetic energy (for each photoelectron) is ''independent'' of the intensity of the light,<ref name="Lenard" /> but depends linearly on the frequency;<ref name="Millikan" /> and if the frequency is too low (corresponding to a photon energy that is less than the ] of the material), no photoelectrons are emitted at all, unless a plurality of photons, whose energetic sum is greater than the energy of the photoelectrons, acts virtually simultaneously (multiphoton effect).<ref>{{Cite journal |last=Smith |first=Richard |year=1962 |title=Two Photon Photoelectric Effect |journal=] |volume=128 |issue=5 |page=2225 |bibcode=1962PhRv..128.2225S |doi=10.1103/PhysRev.128.2225}}</ref><ref>{{cite journal|doi=10.1103/PhysRev.130.2599.4|title=Two-Photon Photoelectric Effect|year=1963|last1=Smith|first1=Richard|journal=]|volume=130|issue=6|page=2599|bibcode = 1963PhRv..130.2599S |doi-access=free}}</ref> Assuming the frequency is high enough to cause the photoelectric effect, a rise in intensity of the light source causes more photoelectrons to be emitted with the same kinetic energy, rather than the same number of photoelectrons to be emitted with higher kinetic energy.<ref name="Lenard" /> | |||
| However, Planck soon realized that his solution was not unique. There were several different solutions, each of which gave a different value for the entropy of the oscillators<ref name="Planck01"/>. To save his theory, Planck had to resort to using the then controversial theory of ],<ref name="Planck01" /> which he described as "an act of despair … I was ready to sacrifice any of my previous convictions about physics."<ref name="Kragh">{{citation | first = Helge | last = Kragh | url = http://physicsworld.com/cws/article/print/373 | title = Max Planck: the reluctant revolutionary | publisher = PhysicsWorld.com | date = 1 December 2000}}</ref> One of his new boundary conditions was | |||
| {{quote|to interpret ''U''<sub>N</sub> not as a continuous, infinitely divisible quantity, but as a discrete quantity composed of an integral number of finite equal parts. Let us call each such part the energy element ε;|<ref name="Planck01" />}} | |||
| With this new condition, Planck had imposed the quantization of the energy of the oscillators, "a purely formal assumption … actually I did not think much about it…" in his own words,<ref>{{citation | title = Quantum Generations: A History of Physics in the Twentieth Century | first = Helge | last = Kragh | year = 1999 | publisher = Princeton University Press | isbn = 0691095523 | page = 62 | url = http://books.google.com/?id=ELrFDIldlawC&printsec=frontcover}}</ref> but one which would revolutionize physics. Applying this new approach to Wien's displacement law showed that the "energy element" must be proportional to the frequency of the oscillator, the first version of what is now termed "Planck's relation": | |||
| :<math>E = h\nu.\,</math> | |||
| Planck was able to calculate the value of ''h'' from experimental data on black-body radiation: his result, {{nowrap|6.55 × 10<sup>−34</sup> J·s}}, is within 1.2% of the currently accepted value.<ref name="Planck01" /> He was also able to make the first determination of the ] ''k''<sub>B</sub> from the same data and theory.<ref name="PlanckNobel">{{citation | first = Max | last = Planck | author-link = Max Planck | title = The Genesis and Present State of Development of the Quantum Theory (Nobel Lecture) | url = http://nobelprize.org/nobel_prizes/physics/laureates/1918/planck-lecture.html | date = 2 June 1920}}</ref> | |||
| Einstein's explanation for these observations was that light itself is quantized; that the energy of light is not transferred continuously as in a classical wave, but only in small "packets" or quanta. The size of these "packets" of energy, which would later be named ]s, was to be the same as Planck's "energy element", giving the modern version of the Planck–Einstein relation: | |||
| Prior to Planck's work, it had been assumed that the energy of a body could take on any value whatsoever – that it was a ]. This is equivalent to saying that the energy element ε (the difference between allowed values of the energy) is zero, and therefore that ''h'' is zero. This is the origin of the often-quoted summary that "the Planck constant is zero in classical physics" or that "classical physics is quantum mechanics at the limit that the Planck constant tends to zero". The Planck constant, of course, is never zero, but it is so small compared to most human experience that its existence had been ignored prior to Planck's work. | |||
| <math display="block">E = hf .</math> | |||
| The black-body problem was revisited in 1905, when ] and ] (on the one hand) and ] (on the other hand) independently proved that classical electromagnetism could ''never'' account for the observed spectrum. These proofs are commonly known as the "]", a name coined by ] in 1911. They contributed greatly (along with Einstein's work on the photoelectric effect) to convincing physicists that Planck's postulate of quantized energy levels was more than a mere mathematical formalism. The very first ] in 1911 was devoted to "the theory of radiation and quanta".<ref>{{citation | url = http://www.solvayinstitutes.be/Conseils%20Solvay/PreviousPhysics.html | title = Previous Solvay Conferences on Physics | accessdate = 12 December 2008 | publisher = International Solvay Institutes}}</ref> Max Planck received the 1918 ] "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta". | |||
| Einstein's postulate was later proven experimentally: the constant of proportionality between the frequency of incident light <math>f</math> and the kinetic energy of photoelectrons <math>E</math> was shown to be equal to the Planck constant <math>h</math>.<ref name="Millikan" /> | |||
| ===Photoelectric effect=== | |||
| {{Main|Photoelectric effect}} | |||
| The photoelectric effect is the emission of electrons (called "photoelectrons") from a surface when light is shined on it. It was first observed by ] in 1839, although credit is usually reserved for ],<ref name="Nobel21">See, eg, {{citation | title = Presentation speech of the 1921 Nobel Prize for Physics | url = http://nobelprize.org/nobel_prizes/physics/laureates/1921/press.html | first = Svante | last = Arrhenius | author-link = Svante Arrhenius | date = 10 December 1922}}</ref> who published the first thorough investigation in 1887. Another particularly thorough investigation was published by ] in 1902.<ref name="Lenard">{{citation | first = P. | last = Lenard | author-link = Philipp Lenard | title = Ueber die lichtelektrische Wirkung | journal = ] | volume = 313 | issue = 5 | pages = 149–98 | year = 1902 | doi = 10.1002/andp.19023130510|bibcode = 1902AnP...313..149L }}</ref> Einstein's 1905 paper<ref>{{Citation |last = Einstein | first = Albert | author-link = Albert Einstein | year = 1905 | title = Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt | url = http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1905_17_132-148.pdf | journal = ] | volume = 17 |issue = 6 | pages = 132–48 | doi = 10.1002/andp.19053220607|bibcode = 1905AnP...322..132E }}</ref> discussing the effect in terms of light quanta would earn him the Nobel Prize in 1921,<ref name="Nobel21" /> when his predictions had been confirmed by the experimental work of ].<ref name="Millikan">{{citation | first = R. A. | last = Millikan |author-link = Robert Andrews Millikan | title = A Direct Photoelectric Determination of Planck's '''h''' | journal = ] | year = 1916 | volume = 7 | issue = 3 | pages = 355–88 | doi = 10.1103/PhysRev.7.355|bibcode = 1916PhRv....7..355M }}</ref> To put it another way, in 1921 at least, Einstein's theories on the photoelectric effect were considered more important than his ] (a name coined, as it happens, by Max Planck).<ref name="Nobel21" /> | |||
| ==== Atomic structure ==== | |||
| Prior to Einstein's paper, electromagnetic radiation such as visible light was considered to behave as a wave: hence the use of the terms "frequency" and "wavelength" to characterise different types of radiation. The energy transferred by a wave in a given time is called its ]. The light from a theatre spotlight is more ''intense'' than the light from a domestic lightbulb; that is to say that the spotlight gives out more energy per unit time (and hence consumes more electricity) than the ordinary bulb, even though the colour of the light might be very similar. Other waves, such as sound or the waves crashing against a seafront, also have their own intensity. However the energy account of the photoelectric effect didn't seem to agree with the wave description of light. | |||
| {{Main|Bohr model}} | |||
| ] | |||
| In 1912 ] developed<ref>{{cite journal |doi=10.1093/mnras/72.8.677 |title=The Constitution of the Solar Corona II |year=1912 |last1=Nicholson |first1=J. W. |journal=Monthly Notices of the Royal Astronomical Society |volume=72 |issue=8 |pages=677–693 |doi-access=free }}</ref> an atomic model and found the angular momentum of the electrons in the model were related by ''h''/2{{pi}}.<ref name="HeilbronPath"> | |||
| The "photoelectrons" emitted as a result of the photoelectric effect have a certain ], which can be measured. This kinetic energy (for each photoelectron) is ''independent'' of the intensity of the light,<ref name="Lenard" /> but depends linearly on the frequency;<ref name="Millikan" /> and if the frequency is too low (corresponding to a kinetic energy for the photoelectrons of zero or less), no photoelectrons are emitted at all, unless there act a plurality of photons virtually simultaneously whose energetic sum is greater than the energy of the photoelectrons (multiphoton effect) <ref>{{Citation|last=Smith |title=Two Photon Photoelectric Effect|journal = Phys Rev |volume=128|page=2225|year=1962|postscript=.}}</ref> Assuming the frequency is high enough to cause the photoelectric effect, a rise in intensity of the light source causes more photoelectrons to be emitted with the same kinetic energy, rather than the same number of photoelectrons to be emitted with higher kinetic energy.<ref name="Lenard" /> | |||
| {{Cite journal |last=Heilbron |first=John L. |year=2013 |title=The path to the quantum atom |journal=] |volume=498 |issue=7452 |pages=27–30 |doi=10.1038/498027a |pmid=23739408 |s2cid=4355108}}</ref><ref name="McCormmach">{{Cite journal |last=McCormmach |first=Russell |year=1966 |title=The Atomic Theory of John William Nicholson |journal=] |volume=3 |issue=2 |pages=160–184 |doi=10.1007/BF00357268 |jstor=41133258 |s2cid=120797894}}</ref> | |||
| Nicholson's nuclear quantum atomic model influenced the development of ] 's atomic model<ref>{{Cite journal |last1=Hirosige |first1=Tetu |last2=Nisio |first2=Sigeko |year=1964 |title=Formation of Bohr's theory of atomic constitution |journal=Japanese Studies in History of Science |volume=3 |pages=6–28}}</ref><ref>{{cite thesis |first=J. L. |last=Heilbron |title=A History of Atomic Models from the Discovery of the Electron to the Beginnings of Quantum Mechanics |degree=PhD |publisher=University of California, Berkeley |year=1964}}</ref><ref name=McCormmach/> and Bohr quoted him in his 1913 paper of the Bohr model of the atom.<ref name="Bohr">{{Cite journal |last=Bohr |first=Neils |year=1913 |title=On the constitution of atoms and molecules |url=https://zenodo.org/record/2493915 |url-status=live |journal=] |series=6th series |volume=26 |issue=151 |pages=1–25 |bibcode=1913PMag...26..476B |doi=10.1080/14786441308634955 |archive-url=https://web.archive.org/web/20230307022713/https://zenodo.org/record/2493915 |archive-date=2023-03-07 |access-date=2023-07-23}}</ref> Bohr's model went beyond Planck's abstract harmonic oscillator concept: an electron in a Bohr atom could only have certain defined energies <math>E_n</math>, defined by | |||
| <math display="block">E_n = -\frac{h c R_{\infty}}{n^2} ,</math> | |||
| Einstein's explanation for these observations was that light itself is quantized; that the energy of light is not transferred continuously as in a classical wave, but only in small "packets" or quanta. The size of these "packets" of energy, which would later be named ]s, was to be the same as Planck's "energy element", giving the modern version of Planck's relation: | |||
| :<math>E = h\nu.\,</math> | |||
| Einstein's postulate was later proven experimentally: the constant of proportionality between the frequency of incident light (''ν'') and the kinetic energy of photoelectrons (''E'') was shown to be equal to the Planck constant (''h'').<ref name="Millikan" /> | |||
| where <math>c</math> is the speed of light in vacuum, <math>R_{\infty}</math> is an experimentally determined constant (the ]) and <math>n \in \{1, 2, 3, ... \}</math>. This approach also allowed Bohr to account for the ], an empirical description of the atomic spectrum of hydrogen, and to account for the value of the Rydberg constant <math>R_{\infty}</math> in terms of other fundamental constants. | |||
| ===Atomic structure=== | |||
| In discussing angular momentum of the electrons in his model Bohr introduced the quantity <math>\frac{h}{2\pi}</math>, now known as the ] as the quantum of ].<ref name="Bohr"/> | |||
| {{Main|Bohr model}} | |||
| ] | |||
| ] introduced the first quantized model of the atom in 1913, in an attempt to overcome a major shortcoming of ] classical model.<ref name="Bohr">{{citation | first = Niels | last = Bohr | author-link = Niels Bohr | title = On the Constitution of Atoms and Molecules | journal = ], Ser. 6 | year = 1913 | volume = 26 | issue = 153 | pages = 1–25 | doi = 10.1080/14786441308634993 }}</ref> In classical electrodynamics, a charge moving in a circle should radiate electromagnetic radiation. If that charge were to be an electron orbiting a ], the radiation would cause it to lose energy and spiral down into the nucleus. Bohr solved this paradox with explicit reference to Planck's work: an electron in a Bohr atom could only have certain defined energies ''E<sub>n</sub>'' | |||
| :<math>E_n = -\frac{h c_0 R_{\infty}}{n^2}</math> | |||
| where ''R''<sub>∞</sub> is an experimentally-determined constant (the ]) and ''n'' is any integer (''n'' = 1, 2, 3, …). Once the electron reached the lowest energy level ({{nowrap|''n'' {{=}} 1}}), it could not get any closer to the nucleus (lower energy). This approach also allowed Bohr to account for the ], an empirical description of the atomic spectrum of hydrogen, and to account for the value of the Rydberg constant ''R''<sub>∞</sub> in terms of other fundamental constants. | |||
| Bohr also introduced the quantity ''h''/2π, now known as the reduced Planck constant, as the quantum of angular momentum. At first, Bohr thought that this was the angular momentum of each electron in an atom: this proved incorrect and, despite developments by Sommerfeld and others, an accurate description of the electron angular momentum proved beyond the Bohr model. The correct quantization rules for electrons – in which the energy reduces to the Bohr-model equation in the case of the hydrogen atom – were given by Heisenberg's ] in 1925 and the ] in 1926: the reduced Planck constant remains the fundamental quantum of angular momentum. In modern terms, if ''J'' is the total angular momentum of a system with rotational invariance, and ''J<sub>z</sub>'' the angular momentum measured along any given direction, these quantities can only take on the values | |||
| :<math> | |||
| \begin{align} | |||
| J^2 = j(j+1) \hbar^2,\qquad & j = 0, \tfrac{1}{2}, 1, \tfrac{3}{2}, \ldots, \\ | |||
| J_z = m \hbar, \qquad\qquad\quad & m = -j, -j+1, \ldots, j. | |||
| \end{align} | |||
| </math> | |||
| ===Uncertainty principle=== | ==== Uncertainty principle ==== | ||
| {{Main|Uncertainty principle}} | {{Main|Uncertainty principle}} | ||
| The Planck constant also occurs in statements of ]'s uncertainty principle. Given |
The Planck constant also occurs in statements of ]'s uncertainty principle. Given numerous particles prepared in the same state, the ] in their position, <math>\Delta x</math>, and the uncertainty in their momentum, <math>\Delta p_{x}</math>, obey | ||
| <math display="block"> \Delta x\, \Delta p_{x} \ge \frac{\hbar}{2} ,</math> | |||
| where the uncertainty is given as the ] of the measured value from its ]. There are |
where the uncertainty is given as the ] of the measured value from its ]. There are several other such pairs of physically measurable ]s which obey a similar rule. One example is time vs. energy. The inverse relationship between the uncertainty of the two conjugate variables forces a tradeoff in quantum experiments, as measuring one quantity more precisely results in the other quantity becoming imprecise. | ||
| In addition to some assumptions underlying the interpretation of certain values in the quantum mechanical formulation, one of the fundamental cornerstones to the entire theory lies in the ] relationship between the position operator <math>\hat{x}</math> and the momentum operator <math>\hat{p}</math>: | In addition to some assumptions underlying the interpretation of certain values in the quantum mechanical formulation, one of the fundamental cornerstones to the entire theory lies in the ] relationship between the ] <math>\hat{x}</math> and the ] <math>\hat{p}</math>: | ||
| :<math> = -i \hbar \delta_{ij}</math> | |||
| where δ<sub>ij</sub> is the ]. | |||
| <math display="block"> = -i \hbar \delta_{ij} ,</math> | |||
| ==Dependent physical constants== | |||
| The following list is based on the 2006 CODATA evaluation;<ref name="CODATA">{{CODATA2006|url=http://physics.nist.gov/cgi-bin/cuu/Value?h}}</ref> for the constants listed below, more than 90% of the uncertainty is due to the uncertainty in the value of the Planck constant, as indicated by the square of the ] (''r''<sup>2</sup> > 0.9, ''r'' > 0.949). The Planck constant is (with one or two exceptions<ref>The main exceptions are the ] ''G'' and the ] ''R''. The uncertainty in the value of the gas constant also affects those physical constants which are related to it, such as the ] and the ].</ref>) the fundamental physical constant which is known to the lowest level of precision, with a ] ''u''<sub>r</sub> of 5.0{{e|−8}}. | |||
| where <math> \delta_{ij}</math> is the ]. | |||
| ===Rest mass of the electron=== | |||
| The normal textbook derivation of the ] ''R''<sub>∞</sub> defines it in terms of the electron mass ''m''<sub>e</sub> and a variety of other physical constants. | |||
| :<math>R_\infty = \frac{m_{\rm e} e^4}{8 \epsilon_0^2 h^3 c_0} = \frac{m_{\rm e} c_0 \alpha^2}{2 h}</math> | |||
| However, the Rydberg constant can be determined very accurately (''u''<sub>r</sub> = 6.6{{e|−12}}) from the atomic spectrum of hydrogen, whereas there is no direct method to measure the mass of a stationary electron in SI units. Hence the equation for the calculation of ''m''<sub>e</sub> becomes | |||
| :<math>m_{\rm e} = \frac{2 R_{\infty} h}{c_0 \alpha^2}</math> | |||
| where ''c''<sub>0</sub> is the speed of light and ''α'' is the ]. The speed of light has an exactly defined value in SI units, and the fine-structure constant can be determined more accurately (''u''<sub>r</sub> = 6.8{{e|−10}}) than the Planck constant: the uncertainty in the value of the electron rest mass is due entirely to the uncertainty in the value of the Planck constant (''r''<sup>2</sup> > 0.999). | |||
| === |
==== Photon energy ==== | ||
| {{Main|Avogadro constant}} | |||
| The Avogadro constant ''N''<sub>A</sub> is determined as the ratio of the mass of one mole of electrons to the mass of a single electron: The mass of one mole of electrons is the "]" of an electron ''A''<sub>r</sub>(e), which can be measured in a ] (''u''<sub>r</sub> = 4.2{{e|−10}}), multiplied by the ] ''M''<sub>u</sub>, which is defined as 0.001 kg/mol. | |||
| :<math>N_{\rm A} = \frac{M_{\rm u} A_{\rm r}({\rm e})}{m_{\rm e}} = \frac{M_{\rm u} A_{\rm r}({\rm e}) c_0 \alpha^2}{2 R_{\infty} h}</math> | |||
| The dependence of the Avogadro constant on the Planck constant (''r''<sup>2</sup> > 0.999) also holds for the physical constants which are related to amount of substance, such as the ]. The uncertainty in the value of the Planck constant limits the knowledge of the masses of atoms and subatomic particles when expressed in SI units. It is possible to measure the masses more precisely in ]s, but not to convert them more precisely into ]s. | |||
| The ] connects the particular ] {{math|''E''}} with its associated wave frequency {{math|''f''}}: | |||
| ===Elementary charge=== | |||
| {{Main|Elementary charge}} | |||
| ] originally defined the fine-structure constant ''α'' as: | |||
| :<math>\alpha\ =\ \frac{e^2}{\hbar c_0 \ 4 \pi \epsilon_0}\ =\ \frac{e^2 c_0 \mu_0}{2 h}</math> | |||
| where ''e'' is the ], ''ε''<sub>0</sub> is the ] (also called the ] of free space), and ''μ''<sub>0</sub> is the ] (also called the ] of free space). The latter two constants have fixed values in the International ]. However, ''α'' can also be determined experimentally, notably by measuring the ] ''g''<sub>e</sub>, then comparing the result with the value predicted by ]. | |||
| <math display="block">E = hf.</math> | |||
| At present, the most precise value for the elementary charge is obtained by rearranging the definition of ''α'' to obtain the following definition of ''e'' in terms of ''α'' and ''h'': | |||
| :<math>e = \sqrt{\frac{2\alpha h}{\mu_0 c_0}}.</math> | |||
| This energy is extremely small in terms of ordinarily perceived everyday objects. | |||
| ===Bohr magneton and nuclear magneton=== | |||
| {{Main|Bohr magneton|Nuclear magneton}} | |||
| The Bohr magneton and the nuclear magneton are units which are used to describe the magnetic properties of the electron and atomic nuclei respectively. The Bohr magneton is the ] which would be expected for an electron if it behaved as a spinning charge according to classical electrodynamics. It is defined in terms of the reduced Planck constant, the elementary charge and the electron mass, all of which depend on the Planck constant: the final dependence on ''h''<sup>½</sup> (''r''<sup>2</sup> > 0.995) can be found by expanding the variables. | |||
| :<math>\mu_{\rm B} = \frac{e \hbar}{2 m_{\rm e}} = \sqrt{\frac{c_0 \alpha^5 h}{32 \pi^2 \mu_0 R_{\infty}^2}}</math> | |||
| The nuclear magneton has a similar definition, but corrected for the fact that the proton is much more massive than the electron. The ratio of the electron relative atomic mass to the proton relative atomic mass can be determined experimentally to a high level of precision (''u''<sub>r</sub> = 4.3{{e|−10}}). | |||
| :<math>\mu_{\rm N} = \mu_{\rm B} \frac{A_{\rm r}({\rm e})}{A_{\rm r}({\rm p})}</math> | |||
| Since the frequency {{math|''f''}}, ] {{math|''λ''}}, and ] {{math|''c''}} are related by <math>f= \frac{c}{\lambda} </math>, the relation can also be expressed as | |||
| == Determination == | |||
| {| class="wikitable" style="float:left; width:50%;" | |||
| |- | |||
| ! Method | |||
| ! Value of ''h''<br/>(10<sup>−34</sup> J·s) | |||
| ! Relative<br/>uncertainty | |||
| ! Ref. | |||
| |- | |||
| | Watt balance | |||
| | {{val|6.62606889|(23)}} | |||
| | align=center | 3.4{{e|−8}} | |||
| | <ref>{{citation | author = Kibble, B. P.; Robinson, I. A.; Belliss, J. H. | year = 1990 | title = A Realization of the SI Watt by the NPL Moving-coil Balance | journal = ] | volume = 27 | issue = 4 | pages = 173–92 | doi = 10.1088/0026-1394/27/4/002|bibcode = 1990Metro..27..173K }}</ref><ref>{{citation | author = Steiner, R.; Newell, D.; Williams, E. | year = 2005 | title = Details of the 1998 Watt Balance Experiment Determining the Planck Constant | url = http://nvl.nist.gov/pub/nistpubs/jres/110/1/j110-1ste.pdf | journal = J. Res. Natl. Inst. Stand. Technol. | volume = 110 | issue = 1 | pages = 1–26}}</ref><ref name="NIST">{{citation | author = Steiner, R. L.; Williams, E. R.; Liu, R.; Newell, D. B. | year = 2007 | title = Uncertainty Improvements of the NIST Electronic Kilogram | journal = IEEE Trans. Instrum. Meas. | volume = 56 | issue = 2 | pages = 592–96 | doi = 10.1109/TIM.2007.890590}}</ref> | |||
| |- | |||
| | X-ray crystal density | |||
| | {{val|6.6260745|(19)}} | |||
| | align=center | 2.9{{e|−7}} | |||
| | <ref>{{citation | author = Fujii, K.; Waseda, A.; Kuramoto, N.; Mizushima, S.; Becker, P.; Bettin, H.; Nicolaus, A.; Kuetgens, U.; Valkiers, S.; Taylor, P.; De Bievre, Paul; Mana, G.; Massa, E.; Matyi, R.; Kessler, E.G., Jr.; Hanke, M. | year = 2005 | title = Present state of the avogadro constant determination from silicon crystals with natural isotopic compositions | journal = IEEE Trans. Instrum. Meas. | volume = 54 | issue = 2 | pages = 854–59 | doi = 10.1109/TIM.2004.843101}}</ref> | |||
| |- | |||
| | Josephson constant | |||
| | {{val|6.6260678|(27)}} | |||
| | align=center | 4.1{{e|−7}} | |||
| | <ref>{{citation | author = Sienknecht, Volkmar; Funck, Torsten | year = 1985 | title = Determination of the SI Volt at the PTB | journal = IEEE Trans. Instrum. Meas. | volume = 34 | issue = 2 | pages = 195–98 | doi = 10.1109/TIM.1985.4315300}}. {{citation | author = Sienknecht, V.; Funck, T. | year = 1986 | title = Realization of the SI Unit Volt by Means of a Voltage Balance | | |||
| journal = ] | volume = 22 | issue = 3 | pages = 209–12 | doi = 10.1088/0026-1394/22/3/018|bibcode = 1986Metro..22..209S }}. {{citation | year = 1991 | title = Determination of the volt with the improved PTB voltage balance | journal = IEEE Trans. Instrum. Meas. | volume = 40 | issue = 2 | pages = 158–61 | doi = 10.1109/TIM.1990.1032905 | author = Funck, T. | last2 = Sienknecht | first2 = V. }}</ref><ref>{{citation | author = Clothier, W. K.; Sloggett, G. J.; Bairnsfather, H.; Currey, M. F.; Benjamin, D. J. | year = 1989 | title = A Determination of the Volt | journal = ] | volume = 26 | issue = 1 | pages = 9–46 | doi = 10.1088/0026-1394/26/1/003|bibcode = 1989Metro..26....9C }}</ref> | |||
| |- | |||
| | Magnetic resonance | |||
| | {{val|6.6260724|(57)}} | |||
| | align=center | 8.6{{e|−7}} | |||
| |<ref>{{citation | author = Kibble, B. P.; Hunt, G. J. | year = 1979 | title = A Measurement of the Gyromagnetic Ratio of the Proton in a Strong Magnetic Field | journal = ] | volume = 15 | issue = 1 | pages = 5–30 | doi = 10.1088/0026-1394/15/1/002|bibcode = 1979Metro..15....5K }}</ref><ref>{{citation | author = Liu, R.; Liu, H.; Jin, T.; Lu, Z.; Du, X.; Xue, S.; Kong, J.; Yu, B.; Zhou, X.; Liu, T.; Zhang, W. | year = 1995 | title = A Recent Determination for the SI Values of ''γ′''<sub>p</sub> and 2''e''/''h'' at NIM | journal = Acta Metrol. Sin. | volume = 16 | issue = 3 | pages = 161–68}}</ref> | |||
| |- | |||
| | Faraday constant | |||
| | {{val|6.6260657|(88)}} | |||
| | align=center | 1.3{{e|−6}} | |||
| | <ref>{{citation | author = Bower, V. E.; Davis, R. S. | year = 1980 | title = The Electrochemical Equivalent of Pure Silver: A Value of the Faraday Constant | journal = J. Res. Natl. Bur. Stand. | volume = 85 | issue = 3 | pages = 175–91}}</ref> | |||
| |- | |||
| | '''CODATA 2010<br/>recommended value''' | |||
| | '''{{val|6.62606957|(29)}}''' | |||
| | align=center | '''4.4{{e|−8}}''' | |||
| | <ref name="2010 CODATA" /> | |||
| |- | |||
| | colspan=4 |The nine recent determinations of the Planck constant cover five separate methods. Where there is more than one recent determination for a given method, the value of ''h'' given here is a weighted mean of the results, as calculated by CODATA. | |||
| |} | |||
| In principle, the Planck constant could be determined by examining the spectrum of a black-body radiator or the kinetic energy of photoelectrons, and this is how its value was first calculated in the early twentieth century. In practice, these are no longer the most accurate methods. The CODATA value quoted here is based on three watt-balance measurements of ''K''<sub>J</sub><sup>2</sup>''R''<sub>K</sub> and one inter-laboratory determination of the molar volume of silicon,<ref name="CODATA" /> but is mostly determined by a 2007 watt-balance measurement made at the U.S. ] (NIST).<ref name="NIST" /> Five other measurements by three different methods were initially considered, but not included in the final refinement as they were too imprecise to affect the result. | |||
| <math display="block">E = \frac{hc}{\lambda} .</math> | |||
| There are both practical and theoretical difficulties in determining ''h''. The practical difficulties can be illustrated by the fact that the two most accurate methods, the ] and the X-ray crystal density method, do not appear to agree with one another. The most likely reason is that the measurement uncertainty for one (or both) of the methods has been estimated too low – it is (or they are) not as precise as is currently believed – but for the time being there is no indication which method is at fault. | |||
| ==== de Broglie wavelength ==== | |||
| The theoretical difficulties arise from the fact that all of the methods ''except'' the X-ray crystal density method rely on the theoretical basis of the ] and the quantum Hall effect. If these theories are slightly inaccurate – though there is no evidence at present to suggest they are – the methods would not give accurate values for the Planck constant. More importantly, the values of the Planck constant obtained in this way cannot be used as tests of the theories without falling into a circular argument. Fortunately, there are other statistical ways of testing the theories, and the theories have yet to be refuted.<ref name="CODATA" /> | |||
| In 1923, ] generalized the Planck–Einstein relation by postulating that the Planck constant represents the proportionality between the momentum and the quantum wavelength of not just the photon, but the quantum wavelength of any particle. This was confirmed by experiments soon afterward. This holds throughout the quantum theory, including ]. The ] {{math|''λ''}} of the particle is given by | |||
| ===Josephson constant=== | |||
| <math display="block">\lambda = \frac{h}{p},</math> | |||
| The Josephson constant ''K''<sub>J</sub> relates the potential difference ''U'' generated by the ] at a "Josephson junction" with the frequency ''ν'' of the microwave radiation. The theoretical treatment of Josephson effect suggests very strongly that ''K''<sub>J</sub> = 2''e''/''h''. | |||
| :<math>K_{\rm J} = \nu/U = 2e/h\,</math> | |||
| The Josephson constant may be measured by comparing the potential difference generated by an array of Josephson junctions with a potential difference which is known in SI ]s. The measurement of the potential difference in SI units is done by allowing an electrostatic force to cancel out a measurable gravitational force. Assuming the validity of the theoretical treatment of the Josephson effect, ''K''<sub>J</sub> is related to the Planck constant by | |||
| :<math>h = \frac{8\alpha}{\mu_0 c_0 K_{\rm J}^2}.</math> | |||
| where {{math|''p''}} denotes the linear ] of a particle, such as a photon, or any other ]. | |||
| ===Watt balance=== | |||
| {{Main|Watt balance}} | |||
| A watt balance is an instrument for comparing two ], one of which is measured in SI ]s and the other of which is measured in ]s. From the definition of the ''conventional'' watt ''W''<sub>90</sub>, this gives a measure of the product ''K''<sub>J</sub><sup>2</sup>''R''<sub>K</sub> in SI units, where ''R''<sub>K</sub> is the ] which appears in the ]. If the theoretical treatments of the Josephson effect and the quantum Hall effect are valid, and in particular assuming that ''R''<sub>K</sub> = ''h''/''e''<sup>2</sup>, the measurement of ''K''<sub>J</sub><sup>2</sup>''R''<sub>K</sub> is a direct determination of the Planck constant. | |||
| :<math>h = \frac{4}{K_{\rm J}^2 R_{\rm K}}</math> | |||
| The ] with angular frequency {{math|1=''ω'' = 2''πf''}} is given by | |||
| ===Magnetic resonance=== | |||
| {{Main|Gyromagnetic ratio}} | |||
| The gyromagnetic ratio ''γ'' is the constant of proportionality between the frequency ''ν'' of ] (or ] for electrons) and the applied magnetic field ''B'': ''ν'' = ''γB''. It is difficult to measure gyromagnetic ratios precisely because of the difficulties in precisely measuring ''B'', but the value for ]s in ] at 25 °C is known to better than one ]. The protons are said to be "shielded" from the applied magnetic field by the electrons in the water molecule, the same effect that gives rise to ] in NMR spectroscopy, and this is indicated by a prime on the symbol for the gyromagnetic ratio, ''γ′''<sub>p</sub>. The gyromagnetic ratio is related to the shielded proton magnetic moment ''μ′''<sub>p</sub>, the ] ''I'' (''I'' = {{frac|1|2}} for protons) and the reduced Planck constant. | |||
| :<math>\gamma^{\prime}_{\rm p} = \frac{\mu^{\prime}_{\rm p}}{I \hbar} = \frac{2 \mu^{\prime}_{\rm p}}{\hbar}</math> | |||
| The ratio of the shielded proton magnetic moment ''μ′''<sub>p</sub> to the electron magnetic moment ''μ''<sub>e</sub> can be measured separately and to high precision, as the imprecisely-known value of the applied magnetic field cancels itself out in taking the ratio. The value of ''μ''<sub>e</sub> in Bohr magnetons is also known: it is half the electron g-factor ''g''<sub>e</sub>. Hence | |||
| :<math>\mu^{\prime}_{\rm p} = \frac{\mu^{\prime}_{\rm p}}{\mu_{\rm e}} \frac{g_{\rm e} \mu_{\rm B}}{2}</math> | |||
| :<math>\gamma^{\prime}_{\rm p} = \frac{\mu^{\prime}_{\rm p}}{\mu_{\rm e}} \frac{g_{\rm e} \mu_{\rm B}}{\hbar}.</math> | |||
| A further complication is that the measurement of ''γ′''<sub>p</sub> involves the measurement of an electric current: this is invariably measured in ''conventional'' amperes rather than in SI ]s, so a conversion factor is required. The symbol ''Γ′''<sub>p-90</sub> is used for the measured gyromagnetic ratio using conventional electrical units. In addition, there are two methods of measuring the value, a "low-field" method and a "high-field" method, and the conversion factors are different in the two cases. Only the high-field value ''Γ′''<sub>p-90</sub>(hi) is of interest in determining the Planck constant. | |||
| :<math>\gamma^{\prime}_{\rm p} = \frac{K_{\rm J-90} R_{\rm K-90}}{K_{\rm J} R_{\rm K}} \Gamma^{\prime}_{\rm p-90}({\rm hi}) = \frac{K_{\rm J-90} R_{\rm K-90} e}{2} \Gamma^{\prime}_{\rm p-90}({\rm hi})</math> | |||
| Substitution gives the expression for the Planck constant in terms of ''Γ′''<sub>p-90</sub>(hi): | |||
| :<math>h = \frac{c_0 \alpha^2 g_{\rm e}}{2 K_{\rm J-90} R_{\rm K-90} R_{\infty} \Gamma^{\prime}_{\rm p-90}({\rm hi})} \frac{\mu_{\rm p}^{\prime}}{\mu_{\rm e}}.</math> | |||
| <math display="block">E = \hbar \omega ,</math> | |||
| ===Faraday constant=== | |||
| {{Main|Faraday constant}} | |||
| The Faraday constant ''F'' is the ] of one mole of electrons, equal to the Avogadro constant ''N''<sub>A</sub> multiplied by the elementary charge ''e''. It can be determined by careful ] experiments, measuring the amount of ] dissolved from an electrode in a given time and for a given electric current. In practice, it is measured in conventional electrical units, and so given the symbol ''F''<sub>90</sub>. Substituting the definitions of ''N''<sub>A</sub> and ''e'', and converting from conventional electrical units to SI units, gives the relation to the Planck constant. | |||
| :<math>h = \frac{c_0 M_{\rm u} A_{\rm r}({\rm e})\alpha^2}{R_{\infty}} \frac{1}{K_{\rm J-90} R_{\rm K-90} F_{90}}</math> | |||
| while its linear momentum relates to | |||
| ===X-ray crystal density=== | |||
| The X-ray crystal density method is primarily a method for determining the Avogadro constant ''N''<sub>A</sub> but as the Avogadro constant is related to the Planck constant it also determines a value for ''h''. The principle behind the method is to determine ''N''<sub>A</sub> as the ratio between the volume of the ] of a crystal, measured by ], and the ] of the substance. Crystals of ] are used, as they are available in high quality and purity by the technology developed for the ] industry. The unit cell volume is calculated from the spacing between two crystal planes referred to as ''d''<sub>220</sub>. The molar volume ''V''<sub>m</sub>(Si) requires a knowledge of the ] of the crystal and the ] of the silicon used. The Planck constant is given by | |||
| :<math>h = \frac{M_{\rm u} A_{\rm r}({\rm e}) c_0 \alpha^2}{R_{\infty}} \frac{\sqrt{2}d^3_{220}}{V_{\rm m}({\rm Si})}.</math> | |||
| <math display="block">p = \hbar k ,</math> | |||
| ==Fixation== | |||
| where {{math|''k''}} is an ]. | |||
| As mentioned above, the numerical value of the Planck constant depends on the system of units used to describe it. Its value in SI units is known to 50 ] but its value in atomic units is known ''exactly'', because of the way the scale of atomic units is defined. The same is true of conventional electrical units, where the Planck constant (noted ''h''<sub>90</sub> to distinguish it from its value in SI units) is given by | |||
| :<math>h_{90} = \frac{4}{K_{J-90}^2 R_{K-90}}</math> | |||
| with ''K''<sub>J–90</sub> and ''R''<sub>K–90</sub> being exactly defined constants. Atomic units and conventional electrical units are very useful in their respective fields, because the uncertainty in the final result doesn't depend on an uncertain conversion factor, only on the uncertainty of the measurement itself. | |||
| These two relations are the temporal and spatial parts of the special relativistic expression using ]. | |||
| There are a number of proposals to redefine certain of the ]s in terms of fundamental physical constants.<ref name="94thCIPM">94th Meeting of the ] (2005). </ref> This has already been done for the metre, which is defined in terms of a fixed value of the speed of light. The most urgent unit on the list for redefinition is the ], whose value has been fixed for all science (since 1889) by the mass of a small cylinder of ]–] alloy kept in vault just outside Paris. While nobody knows if the mass of the ] has "changed" since 1889 – the value 1 kg of its mass expressed in kilograms is by definition unchanged and therein lies one of the problems – it ''is'' known that over such a timescale the many similar Pt–Ir alloy cylinders kept in national laboratories around the world, have changed their relative mass by several tens of parts per million, however carefully they are stored, and the more so, the more they have been taken out and used as mass standards. A change of several tens of micrograms in one kilogram is equivalent to the current uncertainty in the value of the Planck constant in SI units. | |||
| <math display="block">P^\mu = \left(\frac{E}{c}, \vec{p}\right) = \hbar K^\mu = \hbar\left(\frac{\omega}{c}, \vec{k}\right). </math> | |||
| The legal process to change the definition of the kilogram is already underway,<ref name="94thCIPM" /> but it was decided that no final decision would be made before the next meeting of the ] in 2011.<ref name="23rdCGPM">23rd ] (2007). .</ref> The Planck constant is a leading contender to form the basis of the new definition, although not the only one.<ref name="23rdCGPM" /> Possible new definitions include "the mass of a body at rest whose equivalent energy equals the energy of photons whose frequencies sum to {{val|135639274|e=42|u=Hz}}",<ref>{{citation | title = On the redefinition of the kilogram | author = Taylor, B. N.; Mohr, P. J. | url = http://www.iop.org/EJ/article/0026-1394/36/1/11/me9111.pdf | journal = ] | volume = 36 | issue = 1 | year = 1999 | pages = 63–64 | doi = 10.1088/0026-1394/36/1/11|bibcode = 1999Metro..36...63T }}</ref> or simply "the kilogram is defined so that the Planck constant equals {{val|6.62606896|e=-34|u=J·s}}". | |||
| ==== Statistical mechanics ==== | |||
| The ] provided ''Draft Resolution A'' in anticipation of the 24th General Conference on Weights and Measures meeting (2011-10-17 though 2011-10-21), detailing the considerations "On the possible future revision of the International System of Units, the SI".<ref name="24thCGPM">{{Cite web| url=http://www.bipm.org/utils/common/pdf/24_CGPM_Convocation_Draft_Resolution_A.pdf |title=Draft Resolution A: On the possible future revision of the International System of Units, the SI}}</ref> | |||
| Classical ] requires the existence of {{math|''h''}} (but does not define its value).<ref>{{Citation |last1=Giuseppe Morandi |title=Statistical mechanics: an intermediate course |url=https://books.google.com/books?id=MhInFlnNsREC&pg=PA51 |page=84 |year=2001 |access-date=2021-10-31 |archive-url=https://web.archive.org/web/20211206180408/https://books.google.com/books?id=MhInFlnNsREC&pg=PA51 |url-status=live |isbn=978-981-02-4477-4 |archive-date=2021-12-06 |last2=F. Napoli |last3=E. Ercolessi|publisher=World Scientific }}</ref> Eventually, following upon Planck's discovery, it was speculated that physical ] could not take on an arbitrary value, but instead was restricted to integer multiples of a very small quantity, the " ] of action", now called the ''Planck constant''.<ref>{{Cite book |last=ter Haar |first=D. |url=https://archive.org/details/oldquantumtheory0000haar |title=The Old Quantum Theory |publisher=Pergamon Press |year=1967 |isbn=978-0-08-012101-7 |page= |url-access=registration}}</ref> This was a significant conceptual part of the so-called "]" developed by physicists including ], ], and ], in which particle trajectories exist but are ], but quantum laws constrain them based on their action. This view has been replaced by fully modern quantum theory, in which definite trajectories of motion do not even exist; rather, the particle is represented by a wavefunction spread out in space and in time.<ref>{{cite journal |last=Einstein |first=Albert |title=Physics and Reality |url=http://www.kostic.niu.edu/Physics_and_RealityAlbert_Einstein.pdf |journal=Daedalus |volume=132 |issue=4 |page=24 |year=2003 |archive-url=https://web.archive.org/web/20120415132339/http://www.kostic.niu.edu/Physics_and_Reality-Albert_Einstein.pdf |url-status=dead |doi=10.1162/001152603771338742 |s2cid=57559543 |archive-date=2012-04-15 |quote=The question is first: How can one assign a discrete succession of energy values {{math|''H<sub>σ</sub>''}} to a system specified in the sense of classical mechanics (the energy function is a given function of the coordinates {{math |''q<sub>r</sub>''}} and the corresponding momenta {{math |''p<sub>r</sub>''}})? The Planck constant {{math |''h''}} relates the frequency {{math |''H<sub>σ</sub>''/''h''}} to the energy values {{math |''H<sub>σ</sub>''}}. It is therefore sufficient to give to the system a succession of discrete frequency values.}}</ref>{{rp|373}} Related to this is the concept of energy quantization which existed in old quantum theory and also exists in altered form in modern quantum physics. Classical physics cannot explain quantization of energy. | |||
| == Dimension and value == | |||
| Watt balances already measure mass in terms of the Planck constant: at present, standard mass is taken as "fixed" and the measurement is performed to determine the Planck constant but, were the Planck constant to be fixed in SI units, the same experiment would be a measurement of the mass. The relative uncertainty in the measurement would remain the same. | |||
| The Planck constant has the same ] as ] and as ]. In ] units, the Planck constant is expressed with the unit ] per ] (J⋅Hz{{sup|−1}}) or joule-second (J⋅s). | |||
| {{block indent|1=<math>h</math> = {{physconst|h}}}} | |||
| Mass standards could also be constructed from silicon crystals or by other "atom-counting" methods. Such methods require a knowledge of the Avogadro constant, which fixes the proportionality between ] and macroscopic mass but, with a defined value of the Planck constant, ''N''<sub>A</sub> would be known to the same level of uncertainty (if not better) than current methods of comparing macroscopic mass. | |||
| {{block indent|1=<math>\hbar = {h \over 2\pi}</math> = {{physconst|hbar}} = {{val|6.582119569|end=...|e=-16|u=eV⋅s}}.<ref>{{Cite web|url=https://physics.nist.gov/cgi-bin/cuu/Value?hbarev|title=CODATA Value: reduced Planck constant in eV s|website=physics.nist.gov}}</ref>}} | |||
| The above values have been adopted as fixed in the ]. | |||
| ==Computing codes== | |||
| The symbol for the Planck constant is {{unicode|ℎ}}, similar to an italic lowercase ] (''<span style="font-family: serif">h</span>''); the symbol for the reduced Planck constant is {{unicode|ℏ}}, similar to an italic lowercase ] (''<span style="font-family: serif">ħ</span>''). | |||
| Since 2019, the numerical value of the Planck constant has been fixed, with a ] representation. This fixed value is used to define the SI unit of mass, the ]: "the kilogram is defined by taking the fixed numerical value of {{math|''h''}} to be {{val|6.62607015|e=-34}} when expressed in the unit J⋅s, which is equal to kg⋅m<sup>2</sup>⋅s<sup>−1</sup>, where the ] and the ] are defined in terms of ] {{math|''c''}} and duration of ] of the ] of an unperturbed ] atom {{math|Δ''ν''<sub>Cs</sub>}}."<ref>{{SIbrochure9th}}</ref> Technologies of mass ] such as the ] measure refine the value of kilogram applying fixed value of the Planck constant. | |||
| {| class=wikitable style=text-align:right | |||
| |- align=center | |||
| === Significance of the value === | |||
| | align=right | '''character''' || colspan=2 | {{unicode|ℎ}} || colspan=2 | {{unicode|ℏ}} | |||
| The Planck constant is one of the smallest constants used in physics. This reflects the fact that on a scale adapted to humans, where energies are typical of the order of kilojoules and times are typical of the order of seconds or minutes, the Planck constant is very small. When the ] for a physical event approaches the Planck constant, quantum effects dominate.<ref name=FeynmanII>{{Cite web |title=The Feynman Lectures on Physics Vol. II Ch. 19: The Principle of Least Action |url=https://www.feynmanlectures.caltech.edu/II_19.html |access-date=2023-11-03 |website=www.feynmanlectures.caltech.edu}}</ref> | |||
| |- align=center | |||
| | align=right | '''Unicode name''' || colspan=2 | <small>PLANCK CONSTANT</small> || colspan=2 | <small>PLANCK CONSTANT OVER TWO PI</small> | |||
| Equivalently, the order of the Planck constant reflects the fact that everyday objects and systems are made of a ''large'' number of microscopic particles. For example, in ] light (with a ] of 555 ]s or a frequency of {{val|540|u=THz}}) each ] has an energy {{nowrap|1=''E'' = ''hf'' = {{val|3.58|e=-19|u=J}}}}. That is a very small amount of energy in terms of everyday experience, but everyday experience is not concerned with individual photons any more than with individual atoms or molecules. An amount of light more typical in everyday experience (though much larger than the smallest amount perceivable by the human eye) is the energy of one ] of photons; its energy can be computed by multiplying the photon energy by the ], {{physconst|NA|symbol=yes|after=,}} with the result of {{val|216|u=kJ}}, about the food energy in three apples.{{citation needed|date=October 2023}} | |||
| |- | |||
| | align=left | '''character encoding''' || decimal || hex || decimal || hex | |||
| == Reduced Planck constant <span class="anchor" id="Dirac constant"></span> == | |||
| |- | |||
| <!--'Reduced Planck constant' and 'Dirac constant' redirect here--> | |||
| | align=left | ] || 8462 || 210E || 8463 || 210F | |||
| Many equations in quantum physics are customarily written using the '''reduced Planck constant''', | |||
| |- | |||
| <!-- | |||
| | align=left | ] || 226 132 142 || E2 84 8E || 226 132 143 || E2 84 8F | |||
| ***spacing for readability of reference*** | |||
| |- | |||
| --><ref>{{cite book |last1=Schwarz |first1=Patricia M. |last2=Schwarz |first2=John H. |author-link2=John Henry Schwarz|title=Special Relativity: From Einstein to Strings |date=25 March 2004 |publisher=Cambridge University Press |isbn=978-1-139-44950-2 |url=https://books.google.com/books?id=BmhQxWwk0K4C |language=en}}</ref>{{rp|page=}} | |||
| | align=left | ] || &#8462; || &#x210E; || &#8463; || &#x210F; | |||
| equal to <math display="inline">h/(2\pi)</math> and denoted <math display="inline">\hbar</math> (pronounced ''h-bar''<!-- | |||
| |} | |||
| ***spacing for readability of reference*** | |||
| --><ref name="Chabay and Sherwood">{{cite book |last1=Chabay |first1=Ruth W. |author-link1=Ruth Chabay|url=https://books.google.com/books?id=zMWHEAAAQBAJ |title=Matter and Interactions |last2=Sherwood |first2=Bruce A. |date=20 November 2017 |publisher=John Wiley & Sons |isbn=978-1-119-45575-2 |language=en}}</ref>{{rp|page=}}).<!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref name="NIST reduced h">{{cite web |date=20 May 2019 |title=reduced Planck constant |url=https://physics.nist.gov/cgi-bin/cuu/Value?hbar |url-status=live |archive-url=https://web.archive.org/web/20230408225435/https://physics.nist.gov/cgi-bin/cuu/Value?hbar |archive-date=2023-04-08 |access-date=2023-09-03 |website=The NIST Reference on Constants, Units, and Uncertainty |publisher=]}}</ref><!-- | |||
| ***spacing for readability of reference*** | |||
| --> | |||
| The fundamental equations look simpler when written using <math display="inline">\hbar</math> as opposed to {{nowrap|<math display="inline">h</math>,}} and it is usually <math display="inline">\hbar</math> rather than <math display="inline">h</math> that gives the most reliable results when used in ]. | |||
| For example, using ] to estimate the ionization energy of a hydrogen atom, the relevant parameters that determine the ionization energy <math display="inline">E_{\text{i}}</math> are the mass of the electron {{nowrap|<math display="inline">m_{\text{e}}</math>,}} the electron charge {{nowrap|<math display="inline">e</math>,}} and either the Planck constant <math display="inline">h</math> or the reduced Planck constant <math display="inline">\hbar</math>: | |||
| <math display="block">E_{\text{i}} \propto m_{\text{e}} e^{4}/h^{2}\ \text{or}\ \propto m_{\text{e}} e^{4}/\hbar^{2}</math> | |||
| Since both constants have the same dimensions, they will enter the dimensional analysis in the same way, but with <math display="inline">\hbar</math> the estimate is within a factor of two, while with <math display="inline">h</math> the error is closer to | |||
| {{nowrap|<math display="inline">(2\pi)^2 \approx 40</math>.}}<!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite book |last1=Lévy-Leblond|first1=Jean-Marc|author-link1=Jean-Marc Lévy-Leblond|chapter=The meanings of Planck's constant|chapter-url=https://ssqg.ans.pw.edu.pl/en/wp-content/uploads/2021/04/JMLL_Meanings-of-h.pdf|archive-url=https://web.archive.org/web/20231014082224/https://ssqg.ans.pw.edu.pl/en/wp-content/uploads/2021/04/JMLL_Meanings-of-h.pdf|archive-date=2023-10-14|editor-last1=Beltrametti |editor-first1=E. |editor-last2=Rimini |editor-first2=A. |editor-last3=Robotti |editor-first3=Nadia |editor-link3=Nadia Robotti|title=One Hundred Years of H: Pavia, 14-16 September 2000 |date=2002 |publisher=Italian Physical Society |isbn=978-88-7438-003-9 |url=https://books.google.com/books?id=tqbvAAAAMAAJ |language=en}}</ref>{{rp|pages=8–9}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --> | |||
| === Names and symbols === | |||
| The reduced Planck constant is known by many other names: '''reduced Planck's constant'''<!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite book |last1=Huang |first1=Kerson | author-link1=Kerson Huang|title=Quantum Field Theory: From Operators to Path Integrals |date=26 April 2010 |publisher=John Wiley & Sons |isbn=978-3-527-40846-7 |url=https://books.google.com/books?id=5ZWZRpvZzUEC |language=en}}</ref>{{rp|page=}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite book |last1=Schmitz |first1=Kenneth S. |title=Physical Chemistry: Concepts and Theory |date=11 November 2016 |publisher=Elsevier |isbn=978-0-12-800600-9 |url=https://books.google.com/books?id=Y1ydBgAAQBAJ |language=en}}</ref>{{rp|page=}}<!-- | |||
| ***spacing for readability of reference*** | |||
| -->), the '''rationalized Planck constant'''<ref name="Oxford Planck constant"> | |||
| {{cite encyclopedia |title=Planck constant |encyclopedia=A Dictionary of Physics |publisher=Oxford University Press |location=Oxford, UK |url={{google books|plainurl=y|id=YPmFDwAAQBAJ}} |date=2017 |editor-last=Rennie |editor-first=Richard |isbn=978-0198821472 |editor2-last=Law |editor2-first=Jonathan|edition= 7th|series=Oxford Quick Reference | |||
| }}</ref>{{rp|page=}} | |||
| <ref> | |||
| {{cite book |title=The International Encyclopedia of Physical Chemistry and Chemical Physics |date=1960 |publisher=Pergamon Press |url=https://books.google.com/books?id=ufTvAAAAMAAJ |language=en | |||
| }}</ref>{{rp|page=}} | |||
| <ref> | |||
| {{cite book |last1=Vértes |first1=Attila |last2=Nagy |first2=Sándor |last3=Klencsár |first3=Zoltán |last4=Lovas |first4=Rezso György |last5=Rösch |first5=Frank |title=Handbook of Nuclear Chemistry|date=10 December 2010 |publisher=Springer Science & Business Media |isbn=978-1-4419-0719-6 |url=https://books.google.com/books?id=NQyF6KaUScQC |language=en}}</ref>{{rp|page=}} | |||
| (or '''rationalized Planck's constant'''<!-- | |||
| --><ref name="Bethe and Salpeter"> | |||
| {{cite book |editor-last1=Flügge |editor-first1=Siegfried |editor-link1=Siegfried Flügge|title=Handbuch der Physik: Atome I–II |date=1957 |publisher=Springer |url=https://books.google.com/books?id=A-APAQAAMAAJ |last1=Bethe |first1=Hans A. |author-link1=Hans Bethe|last2=Salpeter |first2=Edwin E. |author-link2=Edwin E. Salpeter|chapter=Quantum Mechanics of One- and Two-Electron Atoms |language=en}}</ref>{{rp|page=}} <!-- | |||
| --><ref> | |||
| {{cite book |last1=Lang |first1=Kenneth |title=Astrophysical Formulae: A Compendium for the Physicist and Astrophysicist |date=11 November 2013 |publisher=Springer Science & Business Media |isbn=978-3-662-11188-8 |url=https://books.google.com/books?id=LyzrCAAAQBAJ |language=en}}</ref>{{rp|page=}} <!-- | |||
| -->,<ref> | |||
| {{cite book |last1=Galgani |first1=L. |last2=Carati |first2=A. |last3=Pozzi |first3=B. |chapter=The Problem of the Rate of Thermalization, and the Relations between Classical and Quantum Mechanics |date=December 2002 |pages=111–122 |doi=10.1142/9789812776273_0011|editor-last1=Fabrizio|editor-first1=Mauro |editor-last2=Morro|editor-first2=Angelo|title=Mathematical Models and Methods for Smart Materials, Cortona, Italy, 25 – 29 June 2001 |isbn=978-981-238-235-1 }}</ref>{{rp|page=}} | |||
| the '''Dirac constant'''<!-- | |||
| --><ref name="Fox Student Guide Atomic"> | |||
| {{cite book |last=Fox |first=Mark |url=https://books.google.com/books?id=pVtlDwAAQBAJ |title=A Student's Guide to Atomic Physics |date=14 June 2018 |publisher=Cambridge University Press |isbn=978-1-316-99309-5 |language=en}}</ref>{{rp|page=}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref name="Oxford Planck constant" />{{rp|page=}} <!-- | |||
| --><ref> | |||
| {{cite book |last1=Kleiss |first1=Ronald |title=Quantum Field Theory: A Diagrammatic Approach |date=10 June 2021 |publisher=Cambridge University Press |isbn=978-1-108-78750-5 |url=https://books.google.com/books?id=G_UvEAAAQBAJ |language=en}}</ref>{{rp|page=}} <!-- | |||
| -->(or '''Dirac's constant'''<!-- | |||
| --><ref> | |||
| {{cite book |last1=Zohuri |first1=Bahman |title=Thermal Effects of High Power Laser Energy on Materials |date=5 January 2021 |publisher=Springer Nature |isbn=978-3-030-63064-5 |url=https://books.google.com/books?id=P3gSEAAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}} <!-- | |||
| --><ref> | |||
| {{cite book |last1=Balian |first1=Roger |author-link1=Roger Balian |title=From Microphysics to Macrophysics: Methods and Applications of Statistical Physics |volume=II |date=26 June 2007 |publisher=Springer Science & Business Media |isbn=978-3-540-45480-9 |url=https://books.google.com/books?id=cUY_AAAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}} <!-- | |||
| --><ref> | |||
| {{cite book |last1=Chen |first1=C. Julian |title=Physics of Solar Energy |date=15 August 2011 |publisher=John Wiley & Sons |isbn=978-1-118-04459-9 |url=https://books.google.com/books?id=dFKz6GwSVNEC |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| -->), the '''Dirac <math display="inline">h</math>'''<!-- | |||
| --><ref> | |||
| {{cite encyclopedia |encyclopedia= Britannica |title=Dirac ''h'' |url= https://www.britannica.com/science/Dirac-h|access-date=2023-09-27 |archive-url=https://web.archive.org/web/20230217112008/https://www.britannica.com/science/Dirac-h |archive-date=2023-02-17 |url-status=live }} | |||
| </ref><!-- | |||
| --><ref> | |||
| {{cite book |last1=Shoenberg |first1=D. |author-link1=David Shoenberg|title=Magnetic Oscillations in Metals |date=3 September 2009 |publisher=Cambridge University Press |isbn=978-1-316-58317-3 |url=https://books.google.com/books?id=HM_LCgAAQBAJ |language=en}}</ref>{{rp|page=}} <!-- | |||
| -->(or '''Dirac's <math display="inline">h</math>'''<!-- | |||
| --><ref> | |||
| {{cite book |last1=Powell |first1=John L. |last2=Crasemann |first2=Bernd |title=Quantum Mechanics |date=5 May 2015 |publisher=Courier Dover Publications |isbn=978-0-486-80478-1 |url=https://books.google.com/books?id=GHifCQAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}} <!-- | |||
| -->), the '''Dirac <math display="inline">\hbar</math>'''<!-- | |||
| --><ref> | |||
| {{cite book |last1=Dresden |first1=Max |author-link1=Max Dresden |title=H.A. Kramers Between Tradition and Revolution |date=6 December 2012 |publisher=Springer Science & Business Media |isbn=978-1-4612-4622-0 |url=https://books.google.com/books?id=1ggDCAAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}} <!-- | |||
| -->(or '''Dirac's <math display="inline">\hbar</math>'''<!-- | |||
| --><ref> | |||
| {{cite book |last1=Johnson |first1=R. E. |title=Introduction to Atomic and Molecular Collisions |date=6 December 2012 |publisher=Springer Science & Business Media |isbn=978-1-4684-8448-9 |url=https://books.google.com/books?id=cKPTBwAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}} <!-- | |||
| --><ref> | |||
| {{cite book |last1=Garcia |first1=Alejandro |last2=Henley |first2=Ernest M. |author-link2=Ernest M. Henley|title=Subatomic Physics |date=13 July 2007 |publisher=World Scientific Publishing Company |isbn=978-981-310-167-8 |url=https://books.google.com/books?id=j847DQAAQBAJ |language=en |edition=3rd }}</ref>{{rp|page=}} <!-- | |||
| --><!-- | |||
| <ref> | |||
| {{cite book |last1=Kragh |first1=Helge |author-link1=Helge Kragh|title=Dirac: A Scientific Biography |date=30 March 1990 |publisher=Cambridge University Press |isbn=978-0-521-38089-8 |url=https://www.google.com/books/edition/Dirac/zXm1Bso1VREC |language=en}} | |||
| </ref>{{rp|page=}} | |||
| --><!-- | |||
| -->), and '''h-bar'''.<!-- | |||
| --><ref name="Holbrow et al Modern Introductory Physics"> | |||
| {{cite book |last1=Holbrow |first1=Charles H. | author-link1=Charles H. Holbrow|url=https://books.google.com/books?id=CYE_AAAAQBAJ |title=Modern Introductory Physics |last2=Lloyd |first2=James N. |last3=Amato |first3=Joseph C. |last4=Galvez |first4=Enrique |last5=Parks |first5=M. Elizabeth |date=14 September 2010 |publisher=Springer Science & Business Media |isbn=978-0-387-79080-0 |location=New York |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Polyanin |first1=Andrei D. |author-link1=Andrei Polyanin |url=https://books.google.com/books?id=ejzScufwDRUC |title=A Concise Handbook of Mathematics, Physics, and Engineering Sciences |last2=Chernoutsan |first2=Alexei |date=18 October 2010 |publisher=CRC Press |isbn=978-1-4398-0640-1 |language=en}} | |||
| </ref>{{rp|page=}} <!-- | |||
| -->It is also common to refer to this <math display="inline">\hbar</math> as "Planck's constant"<!-- | |||
| --><ref> | |||
| {{cite book |last1=Dowling |first1=Jonathan P.|author-link1=Jonathan Dowling |title=Schrödinger's Web: Race to Build the Quantum Internet |date=24 August 2020 |publisher=CRC Press |isbn=978-1-000-08017-9 |url=https://books.google.com/books?id=unP2DwAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}} <!-- | |||
| -->{{efn|Notable examples of such usage include ]<!-- | |||
| --><ref name="Landau and Lifshit Quantum Mechanics"> | |||
| {{cite book |last1=Landau |first1=L. D. | author-link1=Lev Landau |url=https://books.google.com/books?id=neBbAwAAQBAJ |title=Quantum Mechanics: Non-Relativistic Theory |last2=Lifshitz |first2=E. M. |author-link2= Evgeny Lifshitz |date=22 October 2013 |publisher=Elsevier |isbn=978-1-4831-4912-7 |language=en}} | |||
| </ref>{{rp|page=}} <!-- | |||
| -->and ],<!-- | |||
| --><ref name="Griffiths Quantum"> | |||
| {{cite book |last1=Griffiths |first1=David J.|author-link= David J. Griffiths |url=https://books.google.com/books?id=zU3bDwAAQBAJ |title=Introduction to Quantum Mechanics |last2=Schroeter |first2=Darrell F. |date=20 November 2019 |publisher=Cambridge University Press |isbn=978-1-108-10314-5 |language=en}} | |||
| </ref>{{rp|page=}} <!-- | |||
| -->but there are many others.<!-- | |||
| --><ref name="Soviet Planck constant"> | |||
| {{cite encyclopedia |title=Planck's constant |encyclopedia=] |publisher=The Gale Group |url=https://encyclopedia2.thefreedictionary.com/Planck%27s+constant |date=1970–1979|edition=3rd}}</ref><!-- | |||
| --><ref> | |||
| {{cite book |last1=Itzykson |first1=Claude | author-link1=Claude Itzykson |last2=Zuber |first2=Jean-Bernard | author-link2=Jean-Bernard Zuber| title=Quantum Field Theory |date=20 September 2012 |publisher=Courier Corporation |isbn=978-0-486-13469-7 |url=https://books.google.com/books?id=CxYCMNrUnTEC |language=en}} | |||
| </ref>{{rp|page=449}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Kaku |first1=Michio | author-link1=Michio Kaku|title=Quantum Field Theory: A Modern Introduction |date=1993 |publisher=Oxford University Press |isbn=978-0-19-507652-3 |url=https://books.google.com/books?id=6J7vAAAAMAAJ |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Bogoli︠u︡bov |first1=Nikolaĭ Nikolaevich | author-link1=Nikolay Bogolyubov|last2=Shirkov |first2=Dmitriy Vasil'evich | author-link2=Dmitry Shirkov |title=Quantum Fields |date=1982 |publisher=Benjamin/Cummings Publishing Company, Advanced Book Program/World Science Division |isbn=978-0-8053-0983-6 |url=https://books.google.com/books?id=wczvAAAAMAAJ |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Aitchison |first1=Ian J. R.|author-link1=Ian Aitchison |last2=Hey |first2=Anthony J. G. |author-link2=Tony Hey|title=Gauge Theories in Particle Physics: A Practical Introduction: From Relativistic Quantum Mechanics to QED |edition=4th |date=17 December 2012 |publisher=CRC Press |isbn=978-1-4665-1299-3 |url=https://books.google.com/books?id=-v6sPfuyUt8C |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=de Wit |first1=B. | author-link1=Bernard de Wit|last2=Smith |first2=J. |title=Field Theory in Particle Physics |volume=1 |date=2 December 2012 |publisher=Elsevier |isbn=978-0-444-59622-2 |url=https://books.google.com/books?id=cCAGmj6XEfkC |language=en}} | |||
| </ref>{{rp|page=}} <!-- | |||
| --><ref> | |||
| {{cite book |last1=Brown |first1=Lowell S. | author-link=Lowell S. Brown|title=Quantum Field Theory |date=1992 |publisher=Cambridge University Press |isbn=978-0-521-46946-3 |url=https://books.google.com/books?id=mKsRAVX1910C |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Buchbinder |first1=Iosif L. |last2=Shapiro |first2=Ilya |title=Introduction to Quantum Field Theory with Applications to Quantum Gravity |date=March 2021 |publisher=Oxford University Press |isbn=978-0-19-883831-9 |url=https://books.google.com/books?id=tL4cEAAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |author-last=Jaffe|author-first=Arthur|author-link=Arthur Jaffe |chapter=9. Where does quantum field theory fit into the big picture?|editor-last1=Cao |editor-first1=Tian Yu |title=Conceptual Foundations of Quantum Field Theory |date=25 March 2004 |publisher=Cambridge University Press |isbn=978-0-521-60272-3 |url=https://books.google.com/books?id=d0wS0EJHZ3MC |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Cabibbo |first1=Nicola |author-link1=Nicola Cabibbo|last2=Maiani |first2=Luciano |author-link2=Luciano Maiani|last3=Benhar |first3=Omar |title=An Introduction to Gauge Theories |date=28 July 2017 |publisher=CRC Press |isbn=978-1-4987-3452-3 |url=https://books.google.com/books?id=6WxGDwAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Casalbuoni |first1=Roberto |title=Introduction To Quantum Field Theory |date=6 April 2017 |publisher=World Scientific Publishing Company |isbn=978-981-314-668-6 |url=https://books.google.com/books?id=MFEyDwAAQBAJ |language=en |edition=2nd }} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Das |first1=Ashok |author-link=Ashok Das|title=Lectures On Quantum Field Theory |edition=2nd|date=24 July 2020 |publisher=World Scientific |isbn=978-981-12-2088-3 |url=https://books.google.com/books?id=gXr1DwAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Desai |first1=Bipin R. |title=Quantum Mechanics with Basic Field Theory |date=2010 |publisher=Cambridge University Press |isbn=978-0-521-87760-2 |url=https://books.google.com/books?id=cScBCJ6wLpYC |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Donoghue |first1=John |last2=Sorbo |first2=Lorenzo |title=A Prelude to Quantum Field Theory |date=8 March 2022 |publisher=Princeton University Press |isbn=978-0-691-22348-3 |url=https://books.google.com/books?id=Wv5FEAAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Folland |first1=Gerald B. |author-link1=Gerald Folland|title=Quantum Field Theory: A Tourist Guide for Mathematicians |date=3 February 2021 |publisher=American Mathematical Society |isbn=978-1-4704-6483-7 |url=https://books.google.com/books?id=nPEbEAAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Fradkin |first1=Eduardo |title=Quantum Field Theory: An Integrated Approach |date=23 March 2021 |publisher=Princeton University Press |isbn=978-0-691-14908-0 |url=https://books.google.com/books?id=ruEIEAAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Gelis |first1=François |title=Quantum Field Theory |date=11 July 2019 |publisher=Cambridge University Press |isbn=978-1-108-48090-1 |url=https://books.google.com/books?id=BzGdDwAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last1=Greiner |first1=Walter|author-link1=Walter Greiner |last2=Reinhardt |first2=Joachim |title=Quantum Electrodynamics |date=9 March 2013 |publisher=Springer Science & Business Media |isbn=978-3-662-05246-4 |url=https://books.google.com/books?id=6y3rCAAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| --><ref> | |||
| {{cite book |last=Liboff |first=Richard L. |author-link=Richard Liboff |url=https://books.google.com/books?id=xMIlAgQSRUsC |title=Introductory Quantum Mechanics |date=2003 |publisher=Pearson Education |isbn=978-81-317-0441-7 |edition=4th |location=San Francisco |language=en}} | |||
| </ref>{{rp|page=846}}<!-- | |||
| --><ref> | |||
| {{cite journal |last=Barut |first=A. O.| author-link=Asım Orhan Barut |date=1 August 1978 |title=The Creation of a Photon: A Heuristic Calculation of Planck's Constant ħ or the Fine Structure Constant α |journal=Zeitschrift für Naturforschung A |volume=33 |issue=8 |pages=993–994 |doi=10.1515/zna-1978-0819|bibcode=1978ZNatA..33..993B |s2cid=45829793 |doi-access=free }} | |||
| </ref><!-- | |||
| --><ref> | |||
| {{cite journal |last1=Kocia |first1=Lucas |last2=Love |first2=Peter |date=12 July 2018 |title=Measurement contextuality and Planck's constant |journal=New Journal of Physics |volume=20 |issue=7 |pages=073020 |doi=10.1088/1367-2630/aacef2|arxiv=1711.08066 |bibcode=2018NJPh...20g3020K |s2cid=73623448 }} | |||
| </ref><!-- | |||
| --><ref> | |||
| {{cite journal |last=Humpherys |first=David |date=28 November 2022 |title=The Implicit Structure of Planck's Constant |journal=European Journal of Applied Physics |volume=4 |issue=6 |pages=22–25 |doi=10.24018/ejphysics.2022.4.6.227|s2cid=254359279 |doi-access=free }} | |||
| </ref>{{rp|page=25}} <!-- | |||
| --><ref> | |||
| {{cite book |last1=Bais |first1=F. Alexander |title=Philosophy of Information |last2=Farmer |first2=J. Doyne | author-link2=J. Doyne Farmer|date=2008 |publisher=North-Holland |isbn=978-0-444-51726-5 |editor-last=Adriaans |editor-first=Pieter |series=Handbook of the Philosophy of Science |volume=8 |publication-place=Amsterdam |chapter=The Physics of Information |editor-last2=van Benthem |editor-first2=Johan |editor-link2=Johan van Benthem (logician) |chapter-url=https://www.sciencedirect.com/science/article/abs/pii/B9780444517265500200 |arxiv=0708.2837}} | |||
| </ref>{{rp|pages=653}}{{excessive citations inline|date=December 2024}}}} <!-- | |||
| -->while retaining the relationship <math display="inline">\hbar = h/(2 \pi)</math>. | |||
| By far the most common symbol for the reduced Planck constant is <math display="inline">\hbar</math>. However, there are some sources that denote it by <math display="inline">h</math> instead, in which case they usually refer to it as the "Dirac <math display="inline">h</math>"<!-- | |||
| --><ref> | |||
| {{cite book |last1=Hirota |first1=E. |last2=Sakakima |first2=H. |last3=Inomata |first3=K. |title=Giant Magneto-Resistance Devices |date=9 March 2013 |publisher=Springer Science & Business Media |isbn=978-3-662-04777-4 |url=https://books.google.com/books?id=mvDrCAAAQBAJ |language=en}} | |||
| </ref>{{rp|page=}} <!-- | |||
| --><ref> | |||
| {{cite journal |last1=Gardner |first1=John H. |title=An Invariance Theory |journal=Encyclia |date=1988 |volume=65 |page=139}} | |||
| </ref> <!-- | |||
| -->(or "Dirac's {{nowrap|<math display="inline">h</math>}}"<!-- | |||
| --><ref> | |||
| {{cite book |last1=Levine |first1=Raphael D. | author-link1=Raphael David Levine|title=Molecular Reaction Dynamics |date=4 June 2009 |publisher=Cambridge University Press |isbn=978-1-139-44287-9 |url=https://books.google.com/books?id=FVqyS31OM7sC |language=en}} | |||
| </ref>{{rp|page=}}<!-- | |||
| ***spacing for readability of reference*** | |||
| -->). | |||
| === History === | |||
| The combination <math display="inline">h/(2\pi)</math> appeared in ]'s 1913 paper,<!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref name="bohr1">{{Cite journal |last=Bohr |first=N. |date=July 1913 |title=I. On the constitution of atoms and molecules |url=https://zenodo.org/record/2493915 |journal=The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science |volume=26 |issue=151 |pages=1–25 |doi=10.1080/14786441308634955|bibcode=1913PMag...26....1B }}</ref>{{rp|page=}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --> where it was denoted by {{nowrap|<math display="inline">M_{0}</math>.}}<ref name="McCormmach"/>{{rp|169}}{{efn|Bohr denoted by <math display="inline">M</math> the angular momentum of the electron around the nucleus, and wrote the quantization condition as {{nowrap|<math display="inline">M=\tau M_{0}</math>,}} where <math display="inline">\tau</math> is a positive integer. (See the ].)}}<!-- | |||
| ***spacing for readability of reference*** | |||
| --> For the next 15 years, the combination continued to appear in the literature, but normally without a separate symbol.<ref name="Mehra and Rechenberg v1p1">{{cite book |last1=Mehra |first1=Jagdish |author-link1=Jagdish Mehra|last2=Rechenberg |first2=Helmut|author-link2=Helmut Rechenberg |title=The Historical Development of Quantum Theory |volume=1|date=3 August 1982 |publisher=Springer New York |isbn=978-0-387-90642-3 |url=https://books.google.com/books?id=oLWNzwEACAAJ |language=en}}</ref>{{rp|page=}}{{efn|Here are some papers that are mentioned in<ref name="Mehra and Rechenberg v1p1"/> and in which <math display="inline">h/(2\pi)</math> appeared without a separate symbol: <!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite journal |last1=Sommerfeld |first1=A. |author-link1=Arnold Sommerfeld|title=Zur Theorie der Balmerschen Serie |journal=Sitzungsberichte der mathematisch-physikalischen Klasse der K. B. Akademie der Wissenschaften zu München |date=1915 |volume=33 |issue=198 |pages=425–458|url=https://static-content.springer.com/esm/art%3A10.1140%2Fepjh%2Fe2013-40053-8/MediaObjects/13129_2013_121_MOESM1_ESM.pdf|doi=10.1140/epjh/e2013-40053-8}}</ref>{{rp|page=428}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite journal |last1=Schwarzschild |first1=K. |author-link1=Karl Schwarzschild|title=Zur Quantenhypothese |journal=Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin|date=1916 |pages=548–568}}</ref>{{rp|page=}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite journal |last1=Ehrenfest |first1=P. |author-link1=Paul Ehrenfest|title=XLVIII. Adiabatic invariants and the theory of quanta |journal=The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science |date=June 1917 |volume=33 |issue=198 |pages=500–513 |doi=10.1080/14786440608635664}}</ref>{{rp|page=}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite journal |last1=Landé |first1=A. |author-link1=Alfred Landé|title=Das Serienspektrum des Heliums |journal=Physikalische Zeitschrift |date=June 1919 |volume=20 |pages= 228–234}}</ref>{{rp|page=}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite journal |last1=Bohr |first1=N.|author-link1=Niels Bohr |title=Über die Serienspektra der Elemente |journal=Zeitschrift für Physik |date=October 1920 |volume=2 |issue=5 |pages=423–469 |doi=10.1007/BF01329978|bibcode=1920ZPhy....2..423B }}</ref>{{rp|page=458}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite journal |last1=Stern |first1=Otto |author-link1=Otto Stern|title=Ein Weg zur experimentellen Prüfung der Richtungsquantelung im Magnetfeld |journal=Zeitschrift für Physik |date=December 1921 |volume=7 |issue=1 |pages=249–253 |doi=10.1007/BF01332793|bibcode=1921ZPhy....7..249S |url=https://books.google.com/books?id=hlZKAAAAMAAJ&dq=%22Ein+Weg+zur+experimentellen+Pr%C3%BCfung+der+Richtungsquantelung%22+%22Bringen+wir+also+ein+Gas+aus+Atomen%22&pg=PA249}}</ref><!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite journal |last1=Heisenberg |first1=Werner|author-link1=Werner Heisenberg |title=Zur Quantentheorie der Linienstruktur und der anomalen Zeemaneflekte |journal=Zeitschrift für Physik |date=December 1922 |volume=8 |issue=1 |pages=273–297 |doi=10.1007/BF01329602|bibcode=1922ZPhy....8..273H }}</ref>{{rp|page=}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite journal |last1=Kramers |first1=H. A.|author-link1=Hans Kramers |last2=Pauli |first2=W.|author-link2=Wolfgang Pauli |title=Zur Theorie der Bandenspektren |journal=Zeitschrift für Physik |date=December 1923 |volume=13 |issue=1 |pages=351–367 |doi=10.1007/BF01328226|bibcode=1923ZPhy...13..351K |url=https://books.google.com/books?id=9PpMAQAAIAAJ&dq=%22negativen+Halogenionen+ein+resultierendes%22&pg=RA1-PA351}}</ref><!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite journal |last1=Born |first1=M. | author-link1=Max Born|last2=Jordan |first2=P.|author-link2=Pascual Jordan |title=Zur Quantenmechanik |journal=Zeitschrift für Physik |date=December 1925 |volume=34 |issue=1 |pages=858–888 |doi=10.1007/BF01328531|bibcode=1925ZPhy...34..858B }}</ref><!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite journal |last1=Dirac |first1=P. A. M.| author-link1=Paul Dirac |title=The fundamental equations of quantum mechanics |journal=Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character |date=December 1925 |volume=109 |issue=752 |pages=642–653 |doi=10.1098/rspa.1925.0150|doi-access=free |bibcode=1925RSPSA.109..642D }}</ref><!-- | |||
| ***spacing for readability of reference*** | |||
| -->.<ref>{{cite journal |last1=Born |first1=M.| author-link1=Max Born |last2=Heisenberg |first2=W.|author-link2=Werner Heisenberg |last3=Jordan |first3=P.|author-link3=Pascual Jordan |title=Zur Quantenmechanik. II. |journal=Zeitschrift für Physik |date=August 1926 |volume=35 |issue=8–9 |pages=557–615 |doi=10.1007/BF01379806|bibcode=1926ZPhy...35..557B }}</ref>}} <!-- | |||
| ***spacing for readability of reference*** | |||
| -->Then, in 1926, in their seminal papers, ] and ] again introduced special symbols for it: <math display="inline">K</math> in the case of Schrödinger,<!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref name="Schrodinger 1926 Erste">{{cite journal |last1=Schrödinger |first1=Erwin |author-link1=Erwin Schrödinger |date=1926 |title=Quantisierung als Eigenwertproblem |journal=Annalen der Physik |volume=384 |issue=4 |pages=361–376 |bibcode=1926AnP...384..361S |doi=10.1002/andp.19263840404 |doi-access=free}}</ref> and <math display="inline">h</math> in the case of Dirac.<!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite journal |last1=Dirac |first1=Paul A. M. |author-link1=Paul Dirac |date=October 1926 |title=On the theory of quantum mechanics |journal=Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character |volume=112 |issue=762 |pages=661–677 |bibcode=1926RSPSA.112..661D |doi=10.1098/rspa.1926.0133 |doi-access=free}}</ref> <!-- | |||
| ***spacing for readability of reference*** | |||
| -->Dirac continued to use <math display="inline">h</math> in this way until 1930,<!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref name="Mehra and Rechenberg v6">{{cite book |last1=Mehra |first1=Jagdish |author-link1=Jagdish Mehra|last2=Rechenberg |first2=Helmut|author-link2=Helmut Rechenberg |title=The Historical Development of Quantum Theory |volume=6|date=2000 |publisher=Springer|location= New York |language=en}}</ref>{{rp|page=}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --> when he introduced the symbol <math display="inline">\hbar</math> in his book ''].''<ref name="Mehra and Rechenberg v6"/>{{rp|page=}} <!-- | |||
| ***spacing for readability of reference*** | |||
| --><ref>{{cite book |last1=Dirac |first1=Paul A. M. |author-link1=Paul Dirac |title=The Principles of Quantum Mechanics |date=1930 |publisher=Clarendon |edition=1st |location=Oxford, U.K.}}</ref><!-- | |||
| --> | |||
| == See also == | == See also == | ||
| {{Portal|Electronics|Chemistry}} | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | * ] | ||
| ==Notes== | == Notes == | ||
| {{notelist}} | |||
| {{Reflist|colwidth=30em}} | |||
| ==References== | == References == | ||
| === Citations === | |||
| * {{Citation | |||
| {{reflist}} | |||
| | last = Barrow | |||
| | first = John D. | |||
| | authorlink = John D. Barrow | |||
| | title = The Constants of Nature; From Alpha to Omega - The Numbers that Encode the Deepest Secrets of the Universe | |||
| | year = 2002 | |||
| | publisher = Pantheon Books | |||
| | location = | |||
| | isbn = 0-375-42221-8 | |||
| }} | |||
| == |
=== Sources === | ||
| {{refbegin}} | |||
| * {{citation |last=Barrow |first=John D. |title=The Constants of Nature; From Alpha to Omega – The Numbers that Encode the Deepest Secrets of the Universe |url=https://archive.org/details/constantsofnatur0000barr |year=2002 |publisher=Pantheon Books |isbn=978-0-375-42221-8 |author-link=John D. Barrow |url-access=registration}} | |||
| {{refend}} | |||
| == External links == | |||
| * | |||
| * | |||
| * | |||
| {{Authority control}} | |||
| ] | ] | ||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 03:52, 20 December 2024
Physical constant in quantum mechanics For the law governing black-body radiation, see Planck's law.| Planck constant | |
|---|---|
| Common symbols | |
| SI unit | joule per hertz (joule second) |
| Other units | electronvolt per hertz (electronvolt second) |
| In SI base units | kg⋅m⋅s |
| Dimension | |
| Value | 6.62607015×10 J⋅Hz 4.135667696...×10 eV⋅Hz |
| Reduced Planck constant | |
|---|---|
| Common symbols | |
| SI unit | joule-second |
| Other units | electronvolt-second |
| In SI base units | kg⋅m⋅s |
| Derivations from other quantities | |
| Dimension | |
| Value | 1.054571817...×10 J⋅s 6.582119569...×10 eV⋅s |
The Planck constant, or Planck's constant, denoted by , is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a matter wave equals the Planck constant divided by the associated particle momentum. The closely related reduced Planck constant, equal to and denoted is commonly used in quantum physics equations.
The constant was postulated by Max Planck in 1900 as a proportionality constant needed to explain experimental black-body radiation. Planck later referred to the constant as the "quantum of action". In 1905, Albert Einstein associated the "quantum" or minimal element of the energy to the electromagnetic wave itself. Max Planck received the 1918 Nobel Prize in Physics "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta".
In metrology, the Planck constant is used, together with other constants, to define the kilogram, the SI unit of mass. The SI units are defined in such a way that, when the Planck constant is expressed in SI units, it has the exact value = 6.62607015×10 J⋅Hz.
History
Origin of the constant
Main article: Planck's law

Planck's constant was formulated as part of Max Planck's successful effort to produce a mathematical expression that accurately predicted the observed spectral distribution of thermal radiation from a closed furnace (black-body radiation). This mathematical expression is now known as Planck's law.
In the last years of the 19th century, Max Planck was investigating the problem of black-body radiation first posed by Kirchhoff some 40 years earlier. Every physical body spontaneously and continuously emits electromagnetic radiation. There was no expression or explanation for the overall shape of the observed emission spectrum. At the time, Wien's law fit the data for short wavelengths and high temperatures, but failed for long wavelengths. Also around this time, but unknown to Planck, Lord Rayleigh had derived theoretically a formula, now known as the Rayleigh–Jeans law, that could reasonably predict long wavelengths but failed dramatically at short wavelengths.
Approaching this problem, Planck hypothesized that the equations of motion for light describe a set of harmonic oscillators, one for each possible frequency. He examined how the entropy of the oscillators varied with the temperature of the body, trying to match Wien's law, and was able to derive an approximate mathematical function for the black-body spectrum, which gave a simple empirical formula for long wavelengths.
Planck tried to find a mathematical expression that could reproduce Wien's law (for short wavelengths) and the empirical formula (for long wavelengths). This expression included a constant, , which is thought to be for Hilfsgröße (auxiliary quantity), and subsequently became known as the Planck constant. The expression formulated by Planck showed that the spectral radiance per unit frequency of a body for frequency ν at absolute temperature T is given by
where is the Boltzmann constant, is the Planck constant, and is the speed of light in the medium, whether material or vacuum.
Planck soon realized that his solution was not unique. There were several different solutions, each of which gave a different value for the entropy of the oscillators. To save his theory, Planck resorted to using the then-controversial theory of statistical mechanics, which he described as "an act of desperation". One of his new boundary conditions was
to interpret UN not as a continuous, infinitely divisible quantity, but as a discrete quantity composed of an integral number of finite equal parts. Let us call each such part the energy element ε;
— Planck, "On the Law of Distribution of Energy in the Normal Spectrum"
With this new condition, Planck had imposed the quantization of the energy of the oscillators, in his own words, "a purely formal assumption ... actually I did not think much about it", but one that would revolutionize physics. Applying this new approach to Wien's displacement law showed that the "energy element" must be proportional to the frequency of the oscillator, the first version of what is now sometimes termed the "Planck–Einstein relation":
Planck was able to calculate the value of from experimental data on black-body radiation: his result, 6.55×10 J⋅s, is within 1.2% of the currently defined value. He also made the first determination of the Boltzmann constant from the same data and theory.
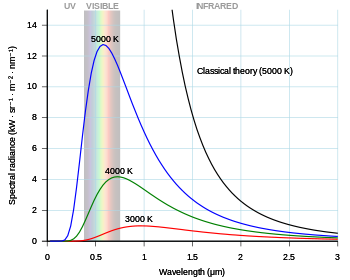
Development and application
The black-body problem was revisited in 1905, when Lord Rayleigh and James Jeans (together) and Albert Einstein independently proved that classical electromagnetism could never account for the observed spectrum. These proofs are commonly known as the "ultraviolet catastrophe", a name coined by Paul Ehrenfest in 1911. They contributed greatly (along with Einstein's work on the photoelectric effect) in convincing physicists that Planck's postulate of quantized energy levels was more than a mere mathematical formalism. The first Solvay Conference in 1911 was devoted to "the theory of radiation and quanta".
Photoelectric effect
Main article: Photoelectric effectThe photoelectric effect is the emission of electrons (called "photoelectrons") from a surface when light is shone on it. It was first observed by Alexandre Edmond Becquerel in 1839, although credit is usually reserved for Heinrich Hertz, who published the first thorough investigation in 1887. Another particularly thorough investigation was published by Philipp Lenard (Lénárd Fülöp) in 1902. Einstein's 1905 paper discussing the effect in terms of light quanta would earn him the Nobel Prize in 1921, after his predictions had been confirmed by the experimental work of Robert Andrews Millikan. The Nobel committee awarded the prize for his work on the photo-electric effect, rather than relativity, both because of a bias against purely theoretical physics not grounded in discovery or experiment, and dissent amongst its members as to the actual proof that relativity was real.
Before Einstein's paper, electromagnetic radiation such as visible light was considered to behave as a wave: hence the use of the terms "frequency" and "wavelength" to characterize different types of radiation. The energy transferred by a wave in a given time is called its intensity. The light from a theatre spotlight is more intense than the light from a domestic lightbulb; that is to say that the spotlight gives out more energy per unit time and per unit space (and hence consumes more electricity) than the ordinary bulb, even though the color of the light might be very similar. Other waves, such as sound or the waves crashing against a seafront, also have their intensity. However, the energy account of the photoelectric effect did not seem to agree with the wave description of light.
The "photoelectrons" emitted as a result of the photoelectric effect have a certain kinetic energy, which can be measured. This kinetic energy (for each photoelectron) is independent of the intensity of the light, but depends linearly on the frequency; and if the frequency is too low (corresponding to a photon energy that is less than the work function of the material), no photoelectrons are emitted at all, unless a plurality of photons, whose energetic sum is greater than the energy of the photoelectrons, acts virtually simultaneously (multiphoton effect). Assuming the frequency is high enough to cause the photoelectric effect, a rise in intensity of the light source causes more photoelectrons to be emitted with the same kinetic energy, rather than the same number of photoelectrons to be emitted with higher kinetic energy.
Einstein's explanation for these observations was that light itself is quantized; that the energy of light is not transferred continuously as in a classical wave, but only in small "packets" or quanta. The size of these "packets" of energy, which would later be named photons, was to be the same as Planck's "energy element", giving the modern version of the Planck–Einstein relation:
Einstein's postulate was later proven experimentally: the constant of proportionality between the frequency of incident light and the kinetic energy of photoelectrons was shown to be equal to the Planck constant .
Atomic structure
Main article: Bohr model
In 1912 John William Nicholson developed an atomic model and found the angular momentum of the electrons in the model were related by h/2π. Nicholson's nuclear quantum atomic model influenced the development of Niels Bohr 's atomic model and Bohr quoted him in his 1913 paper of the Bohr model of the atom. Bohr's model went beyond Planck's abstract harmonic oscillator concept: an electron in a Bohr atom could only have certain defined energies , defined by
where is the speed of light in vacuum, is an experimentally determined constant (the Rydberg constant) and . This approach also allowed Bohr to account for the Rydberg formula, an empirical description of the atomic spectrum of hydrogen, and to account for the value of the Rydberg constant in terms of other fundamental constants. In discussing angular momentum of the electrons in his model Bohr introduced the quantity , now known as the reduced Planck constant as the quantum of angular momentum.
Uncertainty principle
Main article: Uncertainty principleThe Planck constant also occurs in statements of Werner Heisenberg's uncertainty principle. Given numerous particles prepared in the same state, the uncertainty in their position, , and the uncertainty in their momentum, , obey
where the uncertainty is given as the standard deviation of the measured value from its expected value. There are several other such pairs of physically measurable conjugate variables which obey a similar rule. One example is time vs. energy. The inverse relationship between the uncertainty of the two conjugate variables forces a tradeoff in quantum experiments, as measuring one quantity more precisely results in the other quantity becoming imprecise.
In addition to some assumptions underlying the interpretation of certain values in the quantum mechanical formulation, one of the fundamental cornerstones to the entire theory lies in the commutator relationship between the position operator and the momentum operator :
where is the Kronecker delta.
Photon energy
The Planck relation connects the particular photon energy E with its associated wave frequency f:
This energy is extremely small in terms of ordinarily perceived everyday objects.
Since the frequency f, wavelength λ, and speed of light c are related by , the relation can also be expressed as
de Broglie wavelength
In 1923, Louis de Broglie generalized the Planck–Einstein relation by postulating that the Planck constant represents the proportionality between the momentum and the quantum wavelength of not just the photon, but the quantum wavelength of any particle. This was confirmed by experiments soon afterward. This holds throughout the quantum theory, including electrodynamics. The de Broglie wavelength λ of the particle is given by
where p denotes the linear momentum of a particle, such as a photon, or any other elementary particle.
The energy of a photon with angular frequency ω = 2πf is given by
while its linear momentum relates to
where k is an angular wavenumber.
These two relations are the temporal and spatial parts of the special relativistic expression using 4-vectors.
Statistical mechanics
Classical statistical mechanics requires the existence of h (but does not define its value). Eventually, following upon Planck's discovery, it was speculated that physical action could not take on an arbitrary value, but instead was restricted to integer multiples of a very small quantity, the " quantum of action", now called the Planck constant. This was a significant conceptual part of the so-called "old quantum theory" developed by physicists including Bohr, Sommerfeld, and Ishiwara, in which particle trajectories exist but are hidden, but quantum laws constrain them based on their action. This view has been replaced by fully modern quantum theory, in which definite trajectories of motion do not even exist; rather, the particle is represented by a wavefunction spread out in space and in time. Related to this is the concept of energy quantization which existed in old quantum theory and also exists in altered form in modern quantum physics. Classical physics cannot explain quantization of energy.
Dimension and value
The Planck constant has the same dimensions as action and as angular momentum. In SI units, the Planck constant is expressed with the unit joule per hertz (J⋅Hz) or joule-second (J⋅s).
= 6.62607015×10 J⋅Hz = 1.054571817...×10 J⋅s = 6.582119569...×10 eV⋅s.The above values have been adopted as fixed in the 2019 revision of the SI.
Since 2019, the numerical value of the Planck constant has been fixed, with a finite decimal representation. This fixed value is used to define the SI unit of mass, the kilogram: "the kilogram is defined by taking the fixed numerical value of h to be 6.62607015×10 when expressed in the unit J⋅s, which is equal to kg⋅m⋅s, where the metre and the second are defined in terms of speed of light c and duration of hyperfine transition of the ground state of an unperturbed caesium-133 atom ΔνCs." Technologies of mass metrology such as the Kibble balance measure refine the value of kilogram applying fixed value of the Planck constant.
Significance of the value
The Planck constant is one of the smallest constants used in physics. This reflects the fact that on a scale adapted to humans, where energies are typical of the order of kilojoules and times are typical of the order of seconds or minutes, the Planck constant is very small. When the product of energy and time for a physical event approaches the Planck constant, quantum effects dominate.
Equivalently, the order of the Planck constant reflects the fact that everyday objects and systems are made of a large number of microscopic particles. For example, in green light (with a wavelength of 555 nanometres or a frequency of 540 THz) each photon has an energy E = hf = 3.58×10 J. That is a very small amount of energy in terms of everyday experience, but everyday experience is not concerned with individual photons any more than with individual atoms or molecules. An amount of light more typical in everyday experience (though much larger than the smallest amount perceivable by the human eye) is the energy of one mole of photons; its energy can be computed by multiplying the photon energy by the Avogadro constant, NA = 6.02214076×10 mol, with the result of 216 kJ, about the food energy in three apples.
Reduced Planck constant
Many equations in quantum physics are customarily written using the reduced Planck constant, equal to and denoted (pronounced h-bar).
The fundamental equations look simpler when written using as opposed to , and it is usually rather than that gives the most reliable results when used in order-of-magnitude estimates. For example, using dimensional analysis to estimate the ionization energy of a hydrogen atom, the relevant parameters that determine the ionization energy are the mass of the electron , the electron charge , and either the Planck constant or the reduced Planck constant :
Since both constants have the same dimensions, they will enter the dimensional analysis in the same way, but with the estimate is within a factor of two, while with the error is closer to .
Names and symbols
The reduced Planck constant is known by many other names: reduced Planck's constant ), the rationalized Planck constant (or rationalized Planck's constant , the Dirac constant (or Dirac's constant ), the Dirac (or Dirac's ), the Dirac (or Dirac's ), and h-bar. It is also common to refer to this as "Planck's constant" while retaining the relationship .
By far the most common symbol for the reduced Planck constant is . However, there are some sources that denote it by instead, in which case they usually refer to it as the "Dirac " (or "Dirac's ").
History
The combination appeared in Niels Bohr's 1913 paper, where it was denoted by . For the next 15 years, the combination continued to appear in the literature, but normally without a separate symbol. Then, in 1926, in their seminal papers, Schrödinger and Dirac again introduced special symbols for it: in the case of Schrödinger, and in the case of Dirac. Dirac continued to use in this way until 1930, when he introduced the symbol in his book The Principles of Quantum Mechanics.
See also
- Committee on Data of the International Science Council
- International System of Units
- Introduction to quantum mechanics
- List of scientists whose names are used in physical constants
- Planck units
- Wave–particle duality
- Hashgraph
Notes
- Notable examples of such usage include Landau and Lifshitz and Griffiths, but there are many others.
- Bohr denoted by the angular momentum of the electron around the nucleus, and wrote the quantization condition as , where is a positive integer. (See the Bohr model.)
- Here are some papers that are mentioned in and in which appeared without a separate symbol: .
References
Citations
- ^ "Planck constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Archived from the original on 2022-05-27. Retrieved 2023-09-03.
- ^ Planck, Max (1901), "Ueber das Gesetz der Energieverteilung im Normalspectrum" (PDF), Annalen der Physik (in German), 309 (3): 553–63, Bibcode:1901AnP...309..553P, doi:10.1002/andp.19013090310, archived (PDF) from the original on 2012-06-10, retrieved 2008-12-15. English translations:
- "On the Law of Distribution of Energy in the Normal Spectrum". Archived from the original on 2008-04-18.
- "On the Law of Distribution of Energy in the Normal Spectrum" (PDF). Archived from the original (PDF) on 2011-10-06. Retrieved 2011-10-13.
- "Max Planck Nobel Lecture". Archived from the original on 2023-07-14. Retrieved 2023-07-14.
- The International System of Units (PDF) (9th ed.), International Bureau of Weights and Measures, Dec 2022, p. 131, ISBN 978-92-822-2272-0
- ^ "2022 CODATA Value: Planck constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. May 2024. Retrieved 2024-05-18.
- "Resolutions of the 26th CGPM" (PDF). BIPM. 2018-11-16. Archived from the original (PDF) on 2018-11-19. Retrieved 2018-11-20.
- ^ Bitter, Francis; Medicus, Heinrich A. (1973). Fields and particles. New York: Elsevier. pp. 137–144.
- Boya, Luis J. (2004). "The Thermal Radiation Formula of Planck (1900)". arXiv:physics/0402064v1.
- Planck, M. (1914). The Theory of Heat Radiation. Translated by Masius, M. (2nd ed.). P. Blakiston's Son. pp. 6, 168. OL 7154661M.
- Chandrasekhar, S. (1960) . Radiative Transfer (revised reprint ed.). Dover. p. 8. ISBN 978-0-486-60590-6.
- Rybicki, G. B.; Lightman, A. P. (1979). Radiative Processes in Astrophysics. Wiley. p. 22. ISBN 978-0-471-82759-7. Archived from the original on 2020-07-27. Retrieved 2020-05-20.
- Kragh, Helge (1 December 2000), Max Planck: the reluctant revolutionary, PhysicsWorld.com, archived from the original on 2009-01-08
- Kragh, Helge (1999), Quantum Generations: A History of Physics in the Twentieth Century, Princeton University Press, p. 62, ISBN 978-0-691-09552-3, archived from the original on 2021-12-06, retrieved 2021-10-31
- Planck, Max (2 June 1920), The Genesis and Present State of Development of the Quantum Theory (Nobel Lecture), archived from the original on 15 July 2011, retrieved 13 December 2008
- Previous Solvay Conferences on Physics, International Solvay Institutes, archived from the original on 16 December 2008, retrieved 12 December 2008
- ^ See, e.g., Arrhenius, Svante (10 December 1922). "Presentation speech of the 1921 Nobel Prize for Physics". Archived from the original on 4 September 2011. Retrieved 13 December 2008.
- ^ Lenard, P. (1902). "Ueber die lichtelektrische Wirkung". Annalen der Physik. 313 (5): 149–198. Bibcode:1902AnP...313..149L. doi:10.1002/andp.19023130510. Archived from the original on 2019-08-18. Retrieved 2019-07-03.
- Einstein, Albert (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" (PDF). Annalen der Physik. 17 (6): 132–48. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607. Archived (PDF) from the original on 2011-07-09. Retrieved 2009-12-03.
- ^ Millikan, R. A. (1916). "A Direct Photoelectric Determination of Planck's h". Physical Review. 7 (3): 355–88. Bibcode:1916PhRv....7..355M. doi:10.1103/PhysRev.7.355.
- Isaacson, Walter (2007-04-10). Einstein: His Life and Universe. Simon and Schuster. pp. 309–314. ISBN 978-1-4165-3932-2. Archived from the original on 2020-01-09. Retrieved 2021-10-31.
- "The Nobel Prize in Physics 1921". Nobel Foundation. Archived from the original on 2018-07-03. Retrieved 2014-04-23.
- Smith, Richard (1962). "Two Photon Photoelectric Effect". Physical Review. 128 (5): 2225. Bibcode:1962PhRv..128.2225S. doi:10.1103/PhysRev.128.2225.
- Smith, Richard (1963). "Two-Photon Photoelectric Effect". Physical Review. 130 (6): 2599. Bibcode:1963PhRv..130.2599S. doi:10.1103/PhysRev.130.2599.4.
- Nicholson, J. W. (1912). "The Constitution of the Solar Corona II". Monthly Notices of the Royal Astronomical Society. 72 (8): 677–693. doi:10.1093/mnras/72.8.677.
- Heilbron, John L. (2013). "The path to the quantum atom". Nature. 498 (7452): 27–30. doi:10.1038/498027a. PMID 23739408. S2CID 4355108.
- ^ McCormmach, Russell (1966). "The Atomic Theory of John William Nicholson". Archive for History of Exact Sciences. 3 (2): 160–184. doi:10.1007/BF00357268. JSTOR 41133258. S2CID 120797894.
- Hirosige, Tetu; Nisio, Sigeko (1964). "Formation of Bohr's theory of atomic constitution". Japanese Studies in History of Science. 3: 6–28.
- Heilbron, J. L. (1964). A History of Atomic Models from the Discovery of the Electron to the Beginnings of Quantum Mechanics (PhD thesis). University of California, Berkeley.
- ^ Bohr, Neils (1913). "On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 6th series. 26 (151): 1–25. Bibcode:1913PMag...26..476B. doi:10.1080/14786441308634955. Archived from the original on 2023-03-07. Retrieved 2023-07-23.
- Giuseppe Morandi; F. Napoli; E. Ercolessi (2001), Statistical mechanics: an intermediate course, World Scientific, p. 84, ISBN 978-981-02-4477-4, archived from the original on 2021-12-06, retrieved 2021-10-31
- ter Haar, D. (1967). The Old Quantum Theory. Pergamon Press. p. 133. ISBN 978-0-08-012101-7.
- Einstein, Albert (2003). "Physics and Reality" (PDF). Daedalus. 132 (4): 24. doi:10.1162/001152603771338742. S2CID 57559543. Archived from the original (PDF) on 2012-04-15.
The question is first: How can one assign a discrete succession of energy values Hσ to a system specified in the sense of classical mechanics (the energy function is a given function of the coordinates qr and the corresponding momenta pr)? The Planck constant h relates the frequency Hσ/h to the energy values Hσ. It is therefore sufficient to give to the system a succession of discrete frequency values.
- "2022 CODATA Value: reduced Planck constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. May 2024. Retrieved 2024-05-18.
- "CODATA Value: reduced Planck constant in eV s". physics.nist.gov.
- The International System of Units (PDF) (9th ed.), International Bureau of Weights and Measures, Dec 2022, ISBN 978-92-822-2272-0
- "The Feynman Lectures on Physics Vol. II Ch. 19: The Principle of Least Action". www.feynmanlectures.caltech.edu. Retrieved 2023-11-03.
- "2022 CODATA Value: Avogadro constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. May 2024. Retrieved 2024-05-18.
- Schwarz, Patricia M.; Schwarz, John H. (25 March 2004). Special Relativity: From Einstein to Strings. Cambridge University Press. ISBN 978-1-139-44950-2.
- Chabay, Ruth W.; Sherwood, Bruce A. (20 November 2017). Matter and Interactions. John Wiley & Sons. ISBN 978-1-119-45575-2.
- "reduced Planck constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Archived from the original on 2023-04-08. Retrieved 2023-09-03.
- Lévy-Leblond, Jean-Marc (2002). "The meanings of Planck's constant" (PDF). In Beltrametti, E.; Rimini, A.; Robotti, Nadia (eds.). One Hundred Years of H: Pavia, 14-16 September 2000. Italian Physical Society. ISBN 978-88-7438-003-9. Archived from the original (PDF) on 2023-10-14.
- Huang, Kerson (26 April 2010). Quantum Field Theory: From Operators to Path Integrals. John Wiley & Sons. ISBN 978-3-527-40846-7.
- Schmitz, Kenneth S. (11 November 2016). Physical Chemistry: Concepts and Theory. Elsevier. ISBN 978-0-12-800600-9.
- ^ Rennie, Richard; Law, Jonathan, eds. (2017). "Planck constant". A Dictionary of Physics. Oxford Quick Reference (7th ed.). Oxford, UK: Oxford University Press. ISBN 978-0198821472.
- The International Encyclopedia of Physical Chemistry and Chemical Physics. Pergamon Press. 1960.
- Vértes, Attila; Nagy, Sándor; Klencsár, Zoltán; Lovas, Rezso György; Rösch, Frank (10 December 2010). Handbook of Nuclear Chemistry. Springer Science & Business Media. ISBN 978-1-4419-0719-6.
- Bethe, Hans A.; Salpeter, Edwin E. (1957). "Quantum Mechanics of One- and Two-Electron Atoms". In Flügge, Siegfried (ed.). Handbuch der Physik: Atome I–II. Springer.
- Lang, Kenneth (11 November 2013). Astrophysical Formulae: A Compendium for the Physicist and Astrophysicist. Springer Science & Business Media. ISBN 978-3-662-11188-8.
- Galgani, L.; Carati, A.; Pozzi, B. (December 2002). "The Problem of the Rate of Thermalization, and the Relations between Classical and Quantum Mechanics". In Fabrizio, Mauro; Morro, Angelo (eds.). Mathematical Models and Methods for Smart Materials, Cortona, Italy, 25 – 29 June 2001. pp. 111–122. doi:10.1142/9789812776273_0011. ISBN 978-981-238-235-1.
- Fox, Mark (14 June 2018). A Student's Guide to Atomic Physics. Cambridge University Press. ISBN 978-1-316-99309-5.
- Kleiss, Ronald (10 June 2021). Quantum Field Theory: A Diagrammatic Approach. Cambridge University Press. ISBN 978-1-108-78750-5.
- Zohuri, Bahman (5 January 2021). Thermal Effects of High Power Laser Energy on Materials. Springer Nature. ISBN 978-3-030-63064-5.
- Balian, Roger (26 June 2007). From Microphysics to Macrophysics: Methods and Applications of Statistical Physics. Vol. II. Springer Science & Business Media. ISBN 978-3-540-45480-9.
- Chen, C. Julian (15 August 2011). Physics of Solar Energy. John Wiley & Sons. ISBN 978-1-118-04459-9.
- "Dirac h". Britannica. Archived from the original on 2023-02-17. Retrieved 2023-09-27.
- Shoenberg, D. (3 September 2009). Magnetic Oscillations in Metals. Cambridge University Press. ISBN 978-1-316-58317-3.
- Powell, John L.; Crasemann, Bernd (5 May 2015). Quantum Mechanics. Courier Dover Publications. ISBN 978-0-486-80478-1.
- Dresden, Max (6 December 2012). H.A. Kramers Between Tradition and Revolution. Springer Science & Business Media. ISBN 978-1-4612-4622-0.
- Johnson, R. E. (6 December 2012). Introduction to Atomic and Molecular Collisions. Springer Science & Business Media. ISBN 978-1-4684-8448-9.
- Garcia, Alejandro; Henley, Ernest M. (13 July 2007). Subatomic Physics (3rd ed.). World Scientific Publishing Company. ISBN 978-981-310-167-8.
- Holbrow, Charles H.; Lloyd, James N.; Amato, Joseph C.; Galvez, Enrique; Parks, M. Elizabeth (14 September 2010). Modern Introductory Physics. New York: Springer Science & Business Media. ISBN 978-0-387-79080-0.
- Polyanin, Andrei D.; Chernoutsan, Alexei (18 October 2010). A Concise Handbook of Mathematics, Physics, and Engineering Sciences. CRC Press. ISBN 978-1-4398-0640-1.
- Dowling, Jonathan P. (24 August 2020). Schrödinger's Web: Race to Build the Quantum Internet. CRC Press. ISBN 978-1-000-08017-9.
- Landau, L. D.; Lifshitz, E. M. (22 October 2013). Quantum Mechanics: Non-Relativistic Theory. Elsevier. ISBN 978-1-4831-4912-7.
- Griffiths, David J.; Schroeter, Darrell F. (20 November 2019). Introduction to Quantum Mechanics. Cambridge University Press. ISBN 978-1-108-10314-5.
- "Planck's constant". The Great Soviet Encyclopedia (3rd ed.). The Gale Group. 1970–1979.
- Itzykson, Claude; Zuber, Jean-Bernard (20 September 2012). Quantum Field Theory. Courier Corporation. ISBN 978-0-486-13469-7.
- Kaku, Michio (1993). Quantum Field Theory: A Modern Introduction. Oxford University Press. ISBN 978-0-19-507652-3.
- Bogoli︠u︡bov, Nikolaĭ Nikolaevich; Shirkov, Dmitriy Vasil'evich (1982). Quantum Fields. Benjamin/Cummings Publishing Company, Advanced Book Program/World Science Division. ISBN 978-0-8053-0983-6.
- Aitchison, Ian J. R.; Hey, Anthony J. G. (17 December 2012). Gauge Theories in Particle Physics: A Practical Introduction: From Relativistic Quantum Mechanics to QED (4th ed.). CRC Press. ISBN 978-1-4665-1299-3.
- de Wit, B.; Smith, J. (2 December 2012). Field Theory in Particle Physics. Vol. 1. Elsevier. ISBN 978-0-444-59622-2.
- Brown, Lowell S. (1992). Quantum Field Theory. Cambridge University Press. ISBN 978-0-521-46946-3.
- Buchbinder, Iosif L.; Shapiro, Ilya (March 2021). Introduction to Quantum Field Theory with Applications to Quantum Gravity. Oxford University Press. ISBN 978-0-19-883831-9.
- Jaffe, Arthur (25 March 2004). "9. Where does quantum field theory fit into the big picture?". In Cao, Tian Yu (ed.). Conceptual Foundations of Quantum Field Theory. Cambridge University Press. ISBN 978-0-521-60272-3.
- Cabibbo, Nicola; Maiani, Luciano; Benhar, Omar (28 July 2017). An Introduction to Gauge Theories. CRC Press. ISBN 978-1-4987-3452-3.
- Casalbuoni, Roberto (6 April 2017). Introduction To Quantum Field Theory (2nd ed.). World Scientific Publishing Company. ISBN 978-981-314-668-6.
- Das, Ashok (24 July 2020). Lectures On Quantum Field Theory (2nd ed.). World Scientific. ISBN 978-981-12-2088-3.
- Desai, Bipin R. (2010). Quantum Mechanics with Basic Field Theory. Cambridge University Press. ISBN 978-0-521-87760-2.
- Donoghue, John; Sorbo, Lorenzo (8 March 2022). A Prelude to Quantum Field Theory. Princeton University Press. ISBN 978-0-691-22348-3.
- Folland, Gerald B. (3 February 2021). Quantum Field Theory: A Tourist Guide for Mathematicians. American Mathematical Society. ISBN 978-1-4704-6483-7.
- Fradkin, Eduardo (23 March 2021). Quantum Field Theory: An Integrated Approach. Princeton University Press. ISBN 978-0-691-14908-0.
- Gelis, François (11 July 2019). Quantum Field Theory. Cambridge University Press. ISBN 978-1-108-48090-1.
- Greiner, Walter; Reinhardt, Joachim (9 March 2013). Quantum Electrodynamics. Springer Science & Business Media. ISBN 978-3-662-05246-4.
- Liboff, Richard L. (2003). Introductory Quantum Mechanics (4th ed.). San Francisco: Pearson Education. ISBN 978-81-317-0441-7.
- Barut, A. O. (1 August 1978). "The Creation of a Photon: A Heuristic Calculation of Planck's Constant ħ or the Fine Structure Constant α". Zeitschrift für Naturforschung A. 33 (8): 993–994. Bibcode:1978ZNatA..33..993B. doi:10.1515/zna-1978-0819. S2CID 45829793.
- Kocia, Lucas; Love, Peter (12 July 2018). "Measurement contextuality and Planck's constant". New Journal of Physics. 20 (7): 073020. arXiv:1711.08066. Bibcode:2018NJPh...20g3020K. doi:10.1088/1367-2630/aacef2. S2CID 73623448.
- Humpherys, David (28 November 2022). "The Implicit Structure of Planck's Constant". European Journal of Applied Physics. 4 (6): 22–25. doi:10.24018/ejphysics.2022.4.6.227. S2CID 254359279.
- Bais, F. Alexander; Farmer, J. Doyne (2008). "The Physics of Information". In Adriaans, Pieter; van Benthem, Johan (eds.). Philosophy of Information. Handbook of the Philosophy of Science. Vol. 8. Amsterdam: North-Holland. arXiv:0708.2837. ISBN 978-0-444-51726-5.
- Hirota, E.; Sakakima, H.; Inomata, K. (9 March 2013). Giant Magneto-Resistance Devices. Springer Science & Business Media. ISBN 978-3-662-04777-4.
- Gardner, John H. (1988). "An Invariance Theory". Encyclia. 65: 139.
- Levine, Raphael D. (4 June 2009). Molecular Reaction Dynamics. Cambridge University Press. ISBN 978-1-139-44287-9.
- Bohr, N. (July 1913). "I. On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 26 (151): 1–25. Bibcode:1913PMag...26....1B. doi:10.1080/14786441308634955.
- ^ Mehra, Jagdish; Rechenberg, Helmut (3 August 1982). The Historical Development of Quantum Theory. Vol. 1. Springer New York. ISBN 978-0-387-90642-3.
- Sommerfeld, A. (1915). "Zur Theorie der Balmerschen Serie" (PDF). Sitzungsberichte der mathematisch-physikalischen Klasse der K. B. Akademie der Wissenschaften zu München. 33 (198): 425–458. doi:10.1140/epjh/e2013-40053-8.
- Schwarzschild, K. (1916). "Zur Quantenhypothese". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin: 548–568.
- Ehrenfest, P. (June 1917). "XLVIII. Adiabatic invariants and the theory of quanta". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 33 (198): 500–513. doi:10.1080/14786440608635664.
- Landé, A. (June 1919). "Das Serienspektrum des Heliums". Physikalische Zeitschrift. 20: 228–234.
- Bohr, N. (October 1920). "Über die Serienspektra der Elemente". Zeitschrift für Physik. 2 (5): 423–469. Bibcode:1920ZPhy....2..423B. doi:10.1007/BF01329978.
- Stern, Otto (December 1921). "Ein Weg zur experimentellen Prüfung der Richtungsquantelung im Magnetfeld". Zeitschrift für Physik. 7 (1): 249–253. Bibcode:1921ZPhy....7..249S. doi:10.1007/BF01332793.
- Heisenberg, Werner (December 1922). "Zur Quantentheorie der Linienstruktur und der anomalen Zeemaneflekte". Zeitschrift für Physik. 8 (1): 273–297. Bibcode:1922ZPhy....8..273H. doi:10.1007/BF01329602.
- Kramers, H. A.; Pauli, W. (December 1923). "Zur Theorie der Bandenspektren". Zeitschrift für Physik. 13 (1): 351–367. Bibcode:1923ZPhy...13..351K. doi:10.1007/BF01328226.
- Born, M.; Jordan, P. (December 1925). "Zur Quantenmechanik". Zeitschrift für Physik. 34 (1): 858–888. Bibcode:1925ZPhy...34..858B. doi:10.1007/BF01328531.
- Dirac, P. A. M. (December 1925). "The fundamental equations of quantum mechanics". Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. 109 (752): 642–653. Bibcode:1925RSPSA.109..642D. doi:10.1098/rspa.1925.0150.
- Born, M.; Heisenberg, W.; Jordan, P. (August 1926). "Zur Quantenmechanik. II". Zeitschrift für Physik. 35 (8–9): 557–615. Bibcode:1926ZPhy...35..557B. doi:10.1007/BF01379806.
- Schrödinger, Erwin (1926). "Quantisierung als Eigenwertproblem". Annalen der Physik. 384 (4): 361–376. Bibcode:1926AnP...384..361S. doi:10.1002/andp.19263840404.
- Dirac, Paul A. M. (October 1926). "On the theory of quantum mechanics". Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. 112 (762): 661–677. Bibcode:1926RSPSA.112..661D. doi:10.1098/rspa.1926.0133.
- ^ Mehra, Jagdish; Rechenberg, Helmut (2000). The Historical Development of Quantum Theory. Vol. 6. New York: Springer.
- Dirac, Paul A. M. (1930). The Principles of Quantum Mechanics (1st ed.). Oxford, U.K.: Clarendon.
Sources
- Barrow, John D. (2002), The Constants of Nature; From Alpha to Omega – The Numbers that Encode the Deepest Secrets of the Universe, Pantheon Books, ISBN 978-0-375-42221-8
External links
- "The role of the Planck constant in physics" – presentation at 26th CGPM meeting at Versailles, France, November 2018 when voting took place.
- "The Planck constant and its units" – presentation at the 35th Symposium on Chemical Physics at the University of Waterloo, Waterloo, Ontario, Canada, November 3 2019.




 , is a fundamental
, is a fundamental  and denoted
and denoted  is commonly used in quantum physics equations.
is commonly used in quantum physics equations.

 is the
is the  is the
is the 
 and the kinetic energy of photoelectrons
and the kinetic energy of photoelectrons  was shown to be equal to the Planck constant
was shown to be equal to the Planck constant  , defined by
, defined by

 is an experimentally determined constant (the
is an experimentally determined constant (the  . This approach also allowed Bohr to account for the
. This approach also allowed Bohr to account for the  , now known as the
, now known as the  , and the uncertainty in their momentum,
, and the uncertainty in their momentum,  , obey
, obey

 and the
and the  :
:

 is the
is the  , the relation can also be expressed as
, the relation can also be expressed as





 = 1.054571817...×10 J⋅s = 6.582119569...×10 eV⋅s.
= 1.054571817...×10 J⋅s = 6.582119569...×10 eV⋅s.
 are the mass of the electron
are the mass of the electron  , the electron charge
, the electron charge  , and either the Planck constant
, and either the Planck constant 
 .
.
 .
.
 . For the next 15 years, the combination continued to appear in the literature, but normally without a separate symbol. Then, in 1926, in their seminal papers,
. For the next 15 years, the combination continued to appear in the literature, but normally without a separate symbol. Then, in 1926, in their seminal papers,  in the case of Schrödinger, and
in the case of Schrödinger, and  the angular momentum of the electron around the nucleus, and wrote the quantization condition as
the angular momentum of the electron around the nucleus, and wrote the quantization condition as  , where
, where  is a positive integer. (See the
is a positive integer. (See the