| Revision as of 11:29, 29 March 2006 editFresheneesz (talk | contribs)Extended confirmed users9,055 edits rearranging and clarifying← Previous edit | Latest revision as of 00:14, 9 September 2024 edit undo67.249.248.128 (talk) →Practical estimation of radius in the case of real coefficients: Added a wikilink. ✞Tags: Mobile edit Mobile web edit | ||
| (299 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{short description|Domain of convergence of power series}} | |||
| In ], the '''radius of convergence''' of a ] is a non-negative quantity— either a real number or +∞—that represents a range (within the radius) in which the function will converge. | |||
| In ], the '''radius of convergence''' of a ] is the radius of the largest ] at the ] in which the series ]. It is either a non-negative real number or <math>\infty</math>. When it is positive, the power series ] and ] inside the open disk of radius equal to the radius of convergence, and it is the ] of the ] to which it converges. In case of multiple singularities of a function (singularities are those values of the argument for which the function is not defined), the radius of convergence is the shortest or minimum of all the respective distances (which are all non-negative numbers) calculated from the center of the disk of convergence to the respective singularities of the function. | |||
| ==Definition== | |||
| For a power series f defined as: | |||
| For a power series ''f'' defined as: | |||
| :<math>f(z) = |
:<math>f(z) = \sum_{n=0}^\infty c_n (z-a)^n, </math> | ||
| where | where | ||
| :''a'' is a constant (sometimes called the ''center'' of the series since the radius of convergence "centers" around a, like a circle centers around its center), | |||
| :''c''<sub>n</sub> dentoes the nth ] coefficients (note that real numbers are a very common special case of complex numbers), | |||
| :''z'' is a variable and | |||
| :''f''<sub>n</sub> represents the nth term of the series | |||
| *''a'' is a ] constant, the center of the ] of convergence, | |||
| The radius of convergence is defined such that the series converges if | |||
| *''c''<sub>''n''</sub> is the ''n''-th complex coefficient, and | |||
| *''z'' is a complex variable. | |||
| The radius of convergence ''r'' is a nonnegative real number or <math>\infty</math> such that the series converges if | |||
| :<math>|z-a| < r</math> | |||
| :<math> |z-a| <r \!</math> | |||
| and diverges if | and diverges if | ||
| :<math> |z-a| >r \!</math> | |||
| where | |||
| :''r'' is the radius of convergence, which may be a real number or ∞. | |||
| :<math>|z-a| > r.</math> | |||
| In other words, the series converges if ''z'' is close enough to the center. The radius of convergence specifies how close is close enough. The radius of convergence is infinite if the series converges for all ]s ''z''. | |||
| Some may prefer an alternative definition, as existence is obvious: | |||
| : <math>r=\sup \left\{ |z-a|\ \left|\ \sum_{n=0}^\infty c_n(z-a)^n\ \text{ converges } \right.\right\} </math> | |||
| On the boundary, that is, where |''z'' − ''a''| = ''r'', the behavior of the power series may be complicated, and the series may converge for some values of ''z'' and diverge for others. The radius of convergence is infinite if the series converges for all ]s ''z''.<ref>{{Cite book|url=https://books.google.com/books?id=nw9eFnCSDNoC&q=radius+of+convergence|title=Mathematical Analysis-II|date=16 November 2010|publisher=Krishna Prakashan Media|language=en}}</ref> | |||
| ==Finding the radius of convergence== | ==Finding the radius of convergence== | ||
| Two cases arise: | |||
| * The first case is theoretical: when you know all the coefficients <math>c_n</math> then you take certain limits and find the precise radius of convergence. | |||
| The radius of convergence can be found by applying the ] to the terms of the series. The root test is defined as: | |||
| * The second case is practical: when you construct a power series solution of a difficult problem you typically will only know a finite number of terms in a power series, anywhere from a couple of terms to a hundred terms. In this second case, extrapolating a plot estimates the radius of convergence. | |||
| :<math>C = \limsup_{n\rightarrow\infty}\sqrt{|f_n|}</math> | |||
| ===Theoretical radius=== | |||
| and in the case of a power series, this can used to find that: | |||
| :<math>r = \limsup_{n\rightarrow\infty} \frac{1}{\sqrt{|c_n|}}</math> | |||
| where | |||
| :lim sup denotes the ] and | |||
| The radius of convergence can be found by applying the ] to the terms of the series. The root test uses the number | |||
| Note that 1/0 is interpreted as an infinite radius, meaning that ''f'' is an ]. | |||
| :<math>C = \limsup_{n\to\infty}\sqrt{|c_n(z-a)^n|} = \limsup_{n\to\infty} \left(\sqrt{|c_n|}\right) |z-a|</math> | |||
| The ] is usually easier to compute, but the limit may be infinite (i.e. non-existant limit), in which case the root test should be used. The ratio test is defined as: | |||
| :<math>L = \lim_{n\rightarrow\infty}\left|\frac{f_{n+1}}{f_n}\right|</math> | |||
| "lim sup" denotes the ]. The root test states that the series converges if ''C'' < 1 and diverges if ''C'' > 1. It follows that the power series converges if the distance from ''z'' to the center ''a'' is less than | |||
| and in the case of a power series, this can be used to find that: | |||
| :<math> r = \lim_{n\rightarrow\infty} | \frac{c_n}{c_{n+1}} | </math>. | |||
| :<math>r = \frac{1}{\limsup_{n\to\infty}\sqrt{|c_n|}}</math> | |||
| ==Clarity and simplicity result from complexity== | |||
| and diverges if the distance exceeds that number; this statement is the ]. Note that ''r'' = 1/0 is interpreted as an infinite radius, meaning that ''f'' is an ]. | |||
| One of the best examples of clarity and simplicity following from thinking about ''complex'' numbers where confusion would result from thinking about ''real'' numbers is this theorem of ]: | |||
| The limit involved in the ] is usually easier to compute, and when that limit exists, it shows that the radius of convergence is finite. | |||
| <!-- NOTE: The ratio test as usually stated involves c_{n+1}/c_n, but THIS statement correctly uses c_{n+1}/c_n. --> | |||
| ''The nearest point'' means the nearest point in the complex plane, not necessarily on the real line, even if the center and all coefficients are real. See ]; the result stated above is a by-product of the proof found in that article. | |||
| :<math>r = \lim_{n\to\infty} \left| \frac{c_{n}}{c_{n+1}} \right|.</math> | |||
| <!-- NOTE: The ratio test as usually stated involves c_{n+1}/c_n, but THIS statement correctly uses c_n/c_{n+1}. --> | |||
| This is shown as follows. The ratio test says the series converges if | |||
| ===A simple warm-up example=== | |||
| : <math> \lim_{n\to\infty} \frac{|c_{n+1}(z-a)^{n+1}|}{|c_n(z-a)^n|} < 1. </math> | |||
| The arctangent function of ] can be expanded in a power series familiar to calculus students: | |||
| That is equivalent to | |||
| :<math>\arctan(z)=z-\frac{z^3}{3}+\frac{z^5}{5}-\frac{z^7}{7}+\cdots .</math> | |||
| : <math> |z - a| < \frac{1}{\lim_{n\to\infty} \frac{|c_{n+1}|}{|c_n|}} = \lim_{n\to\infty} \left|\frac{c_n}{c_{n+1}}\right|. </math> | |||
| It is easy to apply the ratio test in this case to find that the radius of convergence is 1. But we can also view the matter thus: | |||
| ==={{anchor|Domb–Sykes plot|Domb–Sykes plot}} Practical estimation of radius in the case of real coefficients === | |||
| :<math>\frac{d}{dz}\arctan(z)=\frac{1}{1+z^2}</math> | |||
| <!-- ] redirects here (and so in ] --> | |||
| [[File:Domb Sykes plot Hinch.svg|thumb|right|400px|Plots of the function <math>f(\varepsilon)=\frac{\varepsilon(1+\varepsilon^3)}{\sqrt{1+2\varepsilon}}.</math> <br> | |||
| The solid green line is the ] ] in the Domb–Sykes plot,<ref>See Figure 8.1 in: {{citation| first=E.J. |last=Hinch |year=1991 |title=Perturbation Methods |series=Cambridge Texts in Applied Mathematics |volume=6 |publisher=Cambridge University Press |isbn=0-521-37897-4 |page=146}}</ref> plot (b), which intercepts the vertical axis at −2 and has a slope +1. Thus there is a singularity at <math>\varepsilon=-1/2</math> and so the radius of convergence is <math>r=1/2.</math>]] | |||
| Usually, in scientific applications, only a finite number of coefficients <math>c_n</math> are known. Typically, as <math>n</math> increases, these coefficients settle into a regular behavior determined by the nearest radius-limiting singularity. In this case, two main techniques have been developed, based on the fact that the coefficients of a Taylor series are roughly exponential with ratio <math>1/r</math> where ''r'' is the radius of convergence. | |||
| * The basic case is when the coefficients ultimately share a common sign or alternate in sign. As pointed out earlier in the article, in many cases the limit <math display="inline">\lim_{n\to \infty} {c_n / c_{n-1}}</math> exists, and in this case <math display="inline">1/r = \lim_{n \to \infty} {c_n / c_{n-1}}</math>. Negative <math>r</math> means the convergence-limiting singularity is on the negative axis. Estimate this limit, by plotting the <math>c_n/c_{n-1}</math> versus <math>1/n</math>, and graphically extrapolate to <math>1/n=0</math> (effectively <math>n=\infty</math>) via a ]. The intercept with <math>1/n=0</math> estimates the reciprocal of the radius of convergence, <math>1/r</math>. This plot is called a '''Domb–Sykes plot'''.<ref>{{citation |first1=C. |last1=Domb |first2=M.F. |last2=Sykes |title=On the susceptibility of a ferromagnetic above the Curie point |journal=Proc. R. Soc. Lond. A |volume=240 |pages=214–228 |year=1957 |issue=1221 |doi=10.1098/rspa.1957.0078 |bibcode=1957RSPSA.240..214D |s2cid=119974403 }}</ref> | |||
| and a zero appears in the denominator when ''z''<sup>2</sup> = − 1, i.e., when ''z'' = ''i'' or − ''i''. The center in this power series is at 0. The distance from 0 to either of these two singularities is 1. That is therefore the radius of convergence. | |||
| * The more complicated case is when the signs of the coefficients have a more complex pattern. Mercer and Roberts proposed the following procedure.<ref>{{citation |first1=G.N. |last1=Mercer |first2=A.J. |last2=Roberts |title=A centre manifold description of contaminant dispersion in channels with varying flow properties |journal=SIAM J. Appl. Math. |volume=50 |pages=1547–1565 |year=1990 |doi=10.1137/0150091 |issue=6}}</ref> Define the associated sequence <math display="block">b_n^2=\frac{c_{n+1}c_{n-1} - c_n^2}{c_n c_{n-2} - c_{n-1}^2} \quad n=3,4,5,\ldots.</math> Plot the finitely many known <math>b_n</math> versus <math>1/n</math>, and graphically extrapolate to <math>1/n=0</math> via a linear fit. The intercept with <math>1/n=0</math> estimates the reciprocal of the radius of convergence, <math>1/r</math>.{{pb}} This procedure also estimates two other characteristics of the convergence limiting singularity. Suppose the nearest singularity is of degree <math>p</math> and has angle <math>\pm\theta</math> to the real axis. Then the slope of the linear fit given above is <math>-(p+1)/r</math>. Further, plot <math display="inline">\frac{1}{2} \left(\frac{c_{n-1}b_n}{c_n} + \frac{c_{n+1}}{c_n b_n}\right)</math> versus <math display="inline">1/n^2</math>, then a linear fit extrapolated to <math display="inline">1/n^2=0</math> has intercept at <math>\cos\theta</math>. | |||
| == Radius of convergence in complex analysis == | |||
| (This famous example also immediately gives us a method for calculating the value of <math>\pi</math>. It is an interesting application of ]. In view of Leibniz' test (described in the entry ]) the series | |||
| A power series with a positive radius of convergence can be made into a ] by taking its argument to be a complex variable. The radius of convergence can be characterized by the following theorem: | |||
| : The radius of convergence of a power series ''f'' centered on a point ''a'' is equal to the distance from ''a'' to the nearest point where ''f'' cannot be defined in a way that makes it holomorphic. | |||
| :<math>1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots .</math> | |||
| The set of all points whose distance to ''a'' is strictly less than the radius of convergence is called the ''disk of convergence''. | |||
| converges. So Abel's theorem tells us that the sum of this series must equal | |||
| ] | |||
| :<math>\lim_{z\uparrow 1} \arctan(z)=\frac{\pi}{4}</math><!-- Please don't change \uparrow to \to. Abel's theorem deals only with limits as 1 is approached from below. -->. | |||
| ''The nearest point'' means the nearest point in the ], not necessarily on the real line, even if the center and all coefficients are real. For example, the function | |||
| In view of Leibniz' theorem we can also easily determine | |||
| how many terms of this series we need to use to find <math>\pi</math> to within any required | |||
| accuracy. For a slightly different explanation of this calculation see the entry ].) | |||
| : <math>f(z)=\frac 1 {1+z^2}</math> | |||
| ===A gaudier example=== | |||
| has no singularities on the real line, since <math>1+z^2</math> has no real roots. Its Taylor series about 0 is given by | |||
| :<math>\sum_{n=0}^\infty (-1)^n z^{2n}.</math> | |||
| The root test shows that its radius of convergence is 1. In accordance with this, the function ''f''(''z'') has singularities at ±''i'', which are at a distance 1 from 0. | |||
| For a proof of this theorem, see ]. | |||
| ===A simple example=== | |||
| The arctangent function of ] can be expanded in a power series: | |||
| :<math>\arctan(z)=z-\frac{z^3} 3 + \frac{z^5} 5 -\frac{z^7} 7 +\cdots .</math> | |||
| It is easy to apply the root test in this case to find that the radius of convergence is 1. | |||
| ===A more complicated example=== | |||
| Consider this power series: | Consider this power series: | ||
| :<math>\frac |
:<math>\frac z {e^z-1}=\sum_{n=0}^\infty \frac{B_n}{n!} z^n </math> | ||
| where the |
where the rational numbers ''B''<sub>''n''</sub> are the ]. It may be cumbersome to try to apply the ratio test to find the radius of convergence of this series. But the theorem of complex analysis stated above quickly solves the problem. At ''z'' = 0, there is in effect no singularity since ]. The only non-removable singularities are therefore located at the ''other'' points where the denominator is zero. We solve | ||
| :<math>e^z-1=0</math> | :<math>e^z - 1 = 0</math> | ||
| by recalling that if ''z'' = ''x'' + ''iy'' and ''e'' |
by recalling that if {{math|1=''z'' = ''x'' + ''iy''}} and {{math|1=''e''{{i sup|''iy''}} = cos(''y'') + ''i'' sin(''y'')}} then | ||
| :<math>e^z = e^x e^{iy} = e^x(\cos(y)+i\sin(y)),</math> | :<math>e^z = e^x e^{iy} = e^x(\cos(y)+i\sin(y)),</math> | ||
| and then take ''x'' and ''y'' to be real. Since ''y'' is real, the absolute value of cos(''y'') + ''i'' sin(''y'') is necessarily 1. Therefore, the absolute value of ''e'' |
and then take ''x'' and ''y'' to be real. Since ''y'' is real, the absolute value of {{math|cos(''y'') + ''i'' sin(''y'')}} is necessarily 1. Therefore, the absolute value of ''e''{{i sup|''z''}} can be 1 only if ''e''{{i sup|''x''}} is 1; since ''x'' is real, that happens only if ''x'' = 0. Therefore ''z'' is purely imaginary and {{math|1=cos(''y'') + ''i'' sin(''y'') = 1}}. Since ''y'' is real, that happens only if cos(''y'') = 1 and sin(''y'') = 0, so that ''y'' is an integer multiple of 2{{pi}}. Consequently the singular points of this function occur at | ||
| cos(''y'') + ''i'' sin(''y'') = 1. Since ''y'' is real, that happens only if cos(''y'') = 1 and sin(''y'') = 0, so that ''y'' is an integral multiple of 2π. Since the real part ''x'' is 0 and the imaginary part ''y'' is a nonzero integral multiple of 2π, the solution of our equation is | |||
| :''z'' = a nonzero |
: ''z'' = a nonzero integer multiple of 2{{pi}}''i''. | ||
| The |
The singularities nearest 0, which is the center of the power series expansion, are at ±2{{pi}}''i''. The distance from the center to either of those points is 2{{pi}}, so the radius of convergence is 2{{pi}}. | ||
| == Convergence on the boundary == | |||
| If the power series is expanded around the point ''a'' and the radius of convergence is {{math|''r''}}, then the set of all points {{math|''z''}} such that {{math|1={{mabs|''z'' − ''a''}} = ''r''}} is a ] called the ''boundary'' of the disk of convergence. A power series may diverge at every point on the boundary, or diverge on some points and converge at other points, or converge at all the points on the boundary. Furthermore, even if the series converges everywhere on the boundary (even uniformly), it does not necessarily converge absolutely. | |||
| Example 1: The power series for the function {{math|1=''f''(''z'') = 1/(1 − ''z'')}}, expanded around {{math|1=''z'' = 0}}, which is simply | |||
| :<math> \sum_{n=0}^\infty z^n,</math> | |||
| has radius of convergence 1 and diverges at every point on the boundary. | |||
| Example 2: The power series for {{math|1=''g''(''z'') = −ln(1 − ''z'')}}, expanded around {{math|1=''z'' = 0}}, which is | |||
| :<math> \sum_{n=1}^\infty \frac{1}{n} z^n,</math> | |||
| has radius of convergence 1, and diverges for {{math|1=''z'' = 1}} but converges for all other points on the boundary. The function {{math|''f''(''z'')}} of Example 1 is the ] of {{math|''g''(''z'')}}. | |||
| Example 3: The power series | |||
| :<math> \sum_{n=1}^\infty \frac 1 {n^2} z^n </math> | |||
| has radius of convergence 1 and converges everywhere on the boundary absolutely. If {{math|''h''}} is the function represented by this series on the unit disk, then the derivative of ''h''(''z'') is equal to ''g''(''z'')/''z'' with ''g'' of Example 2. It turns out that {{math|''h''(''z'')}} is the ] function. | |||
| Example 4: The power series | |||
| :<math>\sum_{i=1}^\infty a_i z^i \text{ where } a_i = \frac{(-1)^{n-1}}{2^nn}\text{ for } n = \lfloor\log_2(i)\rfloor+1\text{, the unique integer with }2^{n-1}\le i < 2^n,</math> | |||
| has radius of convergence 1 and converges ] on the entire boundary {{math|1={{mabs|''z''}} = 1}}, but does not ] on the boundary.<ref>{{cite journal |url=https://eudml.org/doc/215384|title=O szeregu potęgowym, który jest zbieżny na całem swem kole zbieżności jednostajnie, ale nie bezwzględnie|journal=Prace Matematyczno-Fizyczne|year=1918|volume=29|issue=1|pages=263–266|last1=Sierpiński|first1=W.|author-link=Wacław Sierpiński}}</ref> | |||
| ==Rate of convergence== | |||
| If we expand the function | |||
| :<math>\sin x = \sum^{\infty}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots\text{ for all } x</math> | |||
| around the point ''x'' = 0, we find out that the radius of convergence of this series is <math>\infty</math> meaning that this series converges for all complex numbers. However, in applications, one is often interested in the precision of a ]. Both the number of terms and the value at which the series is to be evaluated affect the accuracy of the answer. For example, if we want to calculate {{math|sin(0.1)}} accurate up to five decimal places, we only need the first two terms of the series. However, if we want the same precision for {{math|1=''x'' = 1}} we must evaluate and sum the first five terms of the series. For {{math|sin(10)}}, one requires the first 18 terms of the series, and for {{math|sin(100)}} we need to evaluate the first 141 terms. | |||
| So for these particular values the fastest convergence of a power series expansion is at the center, and as one moves away from the center of convergence, the ] slows down until you reach the boundary (if it exists) and cross over, in which case the ] will diverge. | |||
| ==Abscissa of convergence of a Dirichlet series== | |||
| An analogous concept is the ] | |||
| :<math>\sum_{n=1}^\infty \frac{a_n}{n^s}.</math> | |||
| Such a series converges if the real part of ''s'' is greater than a particular number depending on the coefficients ''a''<sub>''n''</sub>: the ] of convergence. | |||
| ==Notes== | |||
| {{reflist}} | |||
| ==References== | |||
| * {{Citation | last1=Brown | first1=James | last2=Churchill | first2=Ruel | title=Complex variables and applications | publisher=] | location=New York | isbn=978-0-07-010905-6 | year=1989}} | |||
| * {{Citation | last1=Stein | first1=Elias | author-link=Elias M. Stein |last2=Shakarchi | first2=Rami | title=Complex Analysis | publisher=] | location=Princeton, New Jersey | isbn=0-691-11385-8 | year=2003}} | |||
| ==See also== | |||
| * ] | |||
| * ] | |||
| * ] | |||
| ==External links== | ==External links== | ||
| * | * | ||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 00:14, 9 September 2024
Domain of convergence of power seriesIn mathematics, the radius of convergence of a power series is the radius of the largest disk at the center of the series in which the series converges. It is either a non-negative real number or . When it is positive, the power series converges absolutely and uniformly on compact sets inside the open disk of radius equal to the radius of convergence, and it is the Taylor series of the analytic function to which it converges. In case of multiple singularities of a function (singularities are those values of the argument for which the function is not defined), the radius of convergence is the shortest or minimum of all the respective distances (which are all non-negative numbers) calculated from the center of the disk of convergence to the respective singularities of the function.
Definition
For a power series f defined as:
where
- a is a complex constant, the center of the disk of convergence,
- cn is the n-th complex coefficient, and
- z is a complex variable.
The radius of convergence r is a nonnegative real number or such that the series converges if
and diverges if
Some may prefer an alternative definition, as existence is obvious:
On the boundary, that is, where |z − a| = r, the behavior of the power series may be complicated, and the series may converge for some values of z and diverge for others. The radius of convergence is infinite if the series converges for all complex numbers z.
Finding the radius of convergence
Two cases arise:
- The first case is theoretical: when you know all the coefficients then you take certain limits and find the precise radius of convergence.
- The second case is practical: when you construct a power series solution of a difficult problem you typically will only know a finite number of terms in a power series, anywhere from a couple of terms to a hundred terms. In this second case, extrapolating a plot estimates the radius of convergence.
Theoretical radius
The radius of convergence can be found by applying the root test to the terms of the series. The root test uses the number
"lim sup" denotes the limit superior. The root test states that the series converges if C < 1 and diverges if C > 1. It follows that the power series converges if the distance from z to the center a is less than
and diverges if the distance exceeds that number; this statement is the Cauchy–Hadamard theorem. Note that r = 1/0 is interpreted as an infinite radius, meaning that f is an entire function.
The limit involved in the ratio test is usually easier to compute, and when that limit exists, it shows that the radius of convergence is finite.
This is shown as follows. The ratio test says the series converges if
That is equivalent to
Practical estimation of radius in the case of real coefficients
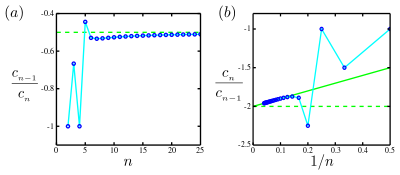
The solid green line is the straight-line asymptote in the Domb–Sykes plot, plot (b), which intercepts the vertical axis at −2 and has a slope +1. Thus there is a singularity at and so the radius of convergence is
Usually, in scientific applications, only a finite number of coefficients are known. Typically, as increases, these coefficients settle into a regular behavior determined by the nearest radius-limiting singularity. In this case, two main techniques have been developed, based on the fact that the coefficients of a Taylor series are roughly exponential with ratio where r is the radius of convergence.
- The basic case is when the coefficients ultimately share a common sign or alternate in sign. As pointed out earlier in the article, in many cases the limit exists, and in this case . Negative means the convergence-limiting singularity is on the negative axis. Estimate this limit, by plotting the versus , and graphically extrapolate to (effectively ) via a linear fit. The intercept with estimates the reciprocal of the radius of convergence, . This plot is called a Domb–Sykes plot.
- The more complicated case is when the signs of the coefficients have a more complex pattern. Mercer and Roberts proposed the following procedure. Define the associated sequence Plot the finitely many known versus , and graphically extrapolate to via a linear fit. The intercept with estimates the reciprocal of the radius of convergence, . This procedure also estimates two other characteristics of the convergence limiting singularity. Suppose the nearest singularity is of degree and has angle to the real axis. Then the slope of the linear fit given above is . Further, plot versus , then a linear fit extrapolated to has intercept at .
Radius of convergence in complex analysis
A power series with a positive radius of convergence can be made into a holomorphic function by taking its argument to be a complex variable. The radius of convergence can be characterized by the following theorem:
- The radius of convergence of a power series f centered on a point a is equal to the distance from a to the nearest point where f cannot be defined in a way that makes it holomorphic.
The set of all points whose distance to a is strictly less than the radius of convergence is called the disk of convergence.

The nearest point means the nearest point in the complex plane, not necessarily on the real line, even if the center and all coefficients are real. For example, the function
has no singularities on the real line, since has no real roots. Its Taylor series about 0 is given by
The root test shows that its radius of convergence is 1. In accordance with this, the function f(z) has singularities at ±i, which are at a distance 1 from 0.
For a proof of this theorem, see analyticity of holomorphic functions.
A simple example
The arctangent function of trigonometry can be expanded in a power series:
It is easy to apply the root test in this case to find that the radius of convergence is 1.
A more complicated example
Consider this power series:
where the rational numbers Bn are the Bernoulli numbers. It may be cumbersome to try to apply the ratio test to find the radius of convergence of this series. But the theorem of complex analysis stated above quickly solves the problem. At z = 0, there is in effect no singularity since the singularity is removable. The only non-removable singularities are therefore located at the other points where the denominator is zero. We solve
by recalling that if z = x + iy and e = cos(y) + i sin(y) then
and then take x and y to be real. Since y is real, the absolute value of cos(y) + i sin(y) is necessarily 1. Therefore, the absolute value of e can be 1 only if e is 1; since x is real, that happens only if x = 0. Therefore z is purely imaginary and cos(y) + i sin(y) = 1. Since y is real, that happens only if cos(y) = 1 and sin(y) = 0, so that y is an integer multiple of 2π. Consequently the singular points of this function occur at
- z = a nonzero integer multiple of 2πi.
The singularities nearest 0, which is the center of the power series expansion, are at ±2πi. The distance from the center to either of those points is 2π, so the radius of convergence is 2π.
Convergence on the boundary
If the power series is expanded around the point a and the radius of convergence is r, then the set of all points z such that |z − a| = r is a circle called the boundary of the disk of convergence. A power series may diverge at every point on the boundary, or diverge on some points and converge at other points, or converge at all the points on the boundary. Furthermore, even if the series converges everywhere on the boundary (even uniformly), it does not necessarily converge absolutely.
Example 1: The power series for the function f(z) = 1/(1 − z), expanded around z = 0, which is simply
has radius of convergence 1 and diverges at every point on the boundary.
Example 2: The power series for g(z) = −ln(1 − z), expanded around z = 0, which is
has radius of convergence 1, and diverges for z = 1 but converges for all other points on the boundary. The function f(z) of Example 1 is the derivative of g(z).
Example 3: The power series
has radius of convergence 1 and converges everywhere on the boundary absolutely. If h is the function represented by this series on the unit disk, then the derivative of h(z) is equal to g(z)/z with g of Example 2. It turns out that h(z) is the dilogarithm function.
Example 4: The power series
has radius of convergence 1 and converges uniformly on the entire boundary |z| = 1, but does not converge absolutely on the boundary.
Rate of convergence
If we expand the function
around the point x = 0, we find out that the radius of convergence of this series is meaning that this series converges for all complex numbers. However, in applications, one is often interested in the precision of a numerical answer. Both the number of terms and the value at which the series is to be evaluated affect the accuracy of the answer. For example, if we want to calculate sin(0.1) accurate up to five decimal places, we only need the first two terms of the series. However, if we want the same precision for x = 1 we must evaluate and sum the first five terms of the series. For sin(10), one requires the first 18 terms of the series, and for sin(100) we need to evaluate the first 141 terms.
So for these particular values the fastest convergence of a power series expansion is at the center, and as one moves away from the center of convergence, the rate of convergence slows down until you reach the boundary (if it exists) and cross over, in which case the series will diverge.
Abscissa of convergence of a Dirichlet series
An analogous concept is the abscissa of convergence of a Dirichlet series
Such a series converges if the real part of s is greater than a particular number depending on the coefficients an: the abscissa of convergence.
Notes
- Mathematical Analysis-II. Krishna Prakashan Media. 16 November 2010.
- See Figure 8.1 in: Hinch, E.J. (1991), Perturbation Methods, Cambridge Texts in Applied Mathematics, vol. 6, Cambridge University Press, p. 146, ISBN 0-521-37897-4
- Domb, C.; Sykes, M.F. (1957), "On the susceptibility of a ferromagnetic above the Curie point", Proc. R. Soc. Lond. A, 240 (1221): 214–228, Bibcode:1957RSPSA.240..214D, doi:10.1098/rspa.1957.0078, S2CID 119974403
- Mercer, G.N.; Roberts, A.J. (1990), "A centre manifold description of contaminant dispersion in channels with varying flow properties", SIAM J. Appl. Math., 50 (6): 1547–1565, doi:10.1137/0150091
- Sierpiński, W. (1918). "O szeregu potęgowym, który jest zbieżny na całem swem kole zbieżności jednostajnie, ale nie bezwzględnie". Prace Matematyczno-Fizyczne. 29 (1): 263–266.
References
- Brown, James; Churchill, Ruel (1989), Complex variables and applications, New York: McGraw-Hill, ISBN 978-0-07-010905-6
- Stein, Elias; Shakarchi, Rami (2003), Complex Analysis, Princeton, New Jersey: Princeton University Press, ISBN 0-691-11385-8
 . When it is positive, the power series
. When it is positive, the power series 



 then you take certain limits and find the precise radius of convergence.
then you take certain limits and find the precise radius of convergence.





 and so the radius of convergence is
and so the radius of convergence is 
 increases, these coefficients settle into a regular behavior determined by the nearest radius-limiting singularity. In this case, two main techniques have been developed, based on the fact that the coefficients of a Taylor series are roughly exponential with ratio
increases, these coefficients settle into a regular behavior determined by the nearest radius-limiting singularity. In this case, two main techniques have been developed, based on the fact that the coefficients of a Taylor series are roughly exponential with ratio  where r is the radius of convergence.
where r is the radius of convergence.
 exists, and in this case
exists, and in this case  . Negative
. Negative  means the convergence-limiting singularity is on the negative axis. Estimate this limit, by plotting the
means the convergence-limiting singularity is on the negative axis. Estimate this limit, by plotting the  versus
versus  , and graphically extrapolate to
, and graphically extrapolate to  (effectively
(effectively  ) via a
) via a  Plot the finitely many known
Plot the finitely many known  versus
versus  and has angle
and has angle  to the real axis. Then the slope of the linear fit given above is
to the real axis. Then the slope of the linear fit given above is  . Further, plot
. Further, plot  versus
versus  , then a linear fit extrapolated to
, then a linear fit extrapolated to  has intercept at
has intercept at  .
. .
.
 has no real roots. Its Taylor series about 0 is given by
has no real roots. Its Taylor series about 0 is given by










