| Revision as of 02:31, 6 February 2014 editPatrick0Moran (talk | contribs)Extended confirmed users12,602 edits →Introduction: tweak← Previous edit | Latest revision as of 17:59, 21 November 2024 edit undoCountercheck (talk | contribs)Extended confirmed users8,081 edits delinked duplicate internal linkTag: AWB | ||
| (236 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Physics experiment in quantum mechanics}} | |||
| {{Quantum mechanics|cTopic=Experiments}} | {{Quantum mechanics|cTopic=Experiments}} | ||
| A '''delayed |
A '''delayed-choice quantum eraser''' experiment, first performed by Yoon-Ho Kim, R. Yu, S. P. Kulik, Y. H. Shih and ],<ref name="DCQE">{{cite journal | author = Kim, Yoon-Ho |author2=R. Yu |author3=S. P. Kulik |author4=Y. H. Shih |author5=Marlan Scully | title = A Delayed "Choice" Quantum Eraser | journal = ] | volume = 84 |issue=1 | year = 2000 | pages = 1–5 | doi = 10.1103/PhysRevLett.84.1| arxiv=quant-ph/9903047 | bibcode=2000PhRvL..84....1K | pmid=11015820|s2cid=5099293 }}</ref> and reported in early 1998, is an elaboration on the ] that incorporates concepts considered in ]'s ]. The experiment was designed to investigate peculiar consequences of the well-known ] in quantum mechanics, as well as the consequences of ]. | ||
| The delayed-choice quantum eraser experiment investigates a paradox. If a photon manifests itself as though it had come by a single path to the detector, then "common sense" (which Wheeler and others challenge) says that it must have entered the double-slit device as a ''particle''. If a photon manifests itself as though it had come by two indistinguishable paths, then it must have entered the double-slit device as a ''wave''. Accordingly, if the experimental apparatus is changed while the photon is in mid‑flight, the photon may have to revise its prior "commitment" as to whether to be a wave or a particle. Wheeler pointed out that when these assumptions are applied to a device of interstellar dimensions, a last-minute decision made on Earth on how to observe a photon could alter a situation established millions or even billions of years earlier. | |||
| ==Introduction== | |||
| In the basic ], a very narrow beam of ] from a source that is far enough away to have almost perfectly parallel wave fronts<!-- too large infix subclause! -->, is directed perpendicularly towards a wall pierced by two parallel slit apertures. The widths of the slits and their separation are approximately the same size as the wavelength of the incident light. | |||
| While delayed-choice experiments might seem to allow measurements made in the present to alter events that occurred in the past, this conclusion requires assuming a non-standard view of quantum mechanics. If a photon in flight is instead ] as being in a so-called "]"—that is, if it is allowed the potentiality of manifesting as a particle or wave, but during its time in flight is neither—then there is no causation paradox. This notion of superposition reflects the standard interpretation of quantum mechanics.<ref>{{cite journal |quote=Our results demonstrate that the viewpoint that the system photon behaves either definitely as a wave or definitely as a particle would require faster-than-light communication. Because this would be in strong tension with the special theory of relativity, we believe that such a viewpoint should be given up entirely.|doi=10.1073/pnas.1213201110|pmid=23288900|pmc=3557028|arxiv=1206.6578|bibcode=2013PNAS..110.1221M|title=Quantum erasure with causally disconnected choice|year=2013|last1=Ma|first1=Xiao-Song|last2=Kofler|first2=Johannes|last3=Qarry|first3=Angie|last4=Tetik|first4=Nuray|last5=Scheidl|first5=Thomas|last6=Ursin|first6=Rupert|last7=Ramelow|first7=Sven|last8=Herbst|first8=Thomas|last9=Ratschbacher|first9=Lothar|last10=Fedrizzi|first10=Alessandro|last11=Jennewein|first11=Thomas|last12=Zeilinger|first12=Anton|journal=Proceedings of the National Academy of Sciences|volume=110|issue=4|pages=1221–1226|doi-access=free}}</ref><ref>{{cite journal |arxiv=1205.4926|doi=10.1126/science.1226719|pmid=23118183|bibcode=2012Sci...338..634P|title=A Quantum Delayed-Choice Experiment|year=2012|last1=Peruzzo|first1=A.|last2=Shadbolt|first2=P.|last3=Brunner|first3=N.|last4=Popescu|first4=S.|last5=O'Brien|first5=J. L.|journal=Science|volume=338|issue=6107|pages=634–637|s2cid=3725159}} This experiment uses Bell inequalities to replace the delayed choice devices, but it achieves the same experimental purpose in an elegant and convincing way.</ref> | |||
| If a detection screen (anything from a sheet of white paper to a digital camera) is put on the other side of the double slit wall, a pattern of light and dark fringes will be observed, a pattern that is called an '''interference pattern'''. | |||
| ==Introduction== | |||
| Early in the history of this experiment, scientists discovered that, by decreasing the brightness of the light source sufficiently, individual particles of light that form the interference pattern are detectable. They next tried to discover by which slit a given unit of light (]) had traveled. | |||
| In the basic ], a beam of light (usually from a ]) is directed perpendicularly towards a wall pierced by two parallel slit apertures. If a detection screen (anything from a sheet of white paper to a ]) is put on the other side of the double-slit wall (far enough for light from both slits to overlap), a pattern of light and dark fringes will be observed, a pattern that is called an ''interference pattern''. Other atomic-scale entities such as ] are found to exhibit the same behavior when fired toward a double slit.<ref name="Feynman">{{cite book | |||
| | last = Feynman | |||
| | first = Richard P. | |||
| | author2 = Robert B. Leighton | |||
| | author3 = Matthew Sands | |||
| | title = The Feynman Lectures on Physics, Vol. 3 | |||
| | publisher = Addison-Wesley | |||
| | year = 1965 | |||
| | location = US | |||
| | pages = 1.1–1.8 | |||
| | isbn = 978-0-201-02118-9}}</ref> By decreasing the brightness of the source sufficiently, individual particles that form the interference pattern are detectable.<ref>{{cite journal | last1 = Donati | first1 = O | last2 = Missiroli | first2 = G F | last3 = Pozzi | first3 = G | year = 1973 | title = An Experiment on Electron Interference | journal = American Journal of Physics | volume = 41 | issue = 5| pages = 639–644 | doi = 10.1119/1.1987321 |bibcode = 1973AmJPh..41..639D }}</ref> The emergence of an interference pattern suggests that each particle passing through the slits interferes with itself, and that therefore in some sense the particles are going through both slits at once.<ref name=Greene2003>{{cite book |last=Greene |first=Brian |title=The Elegant Universe |year=2003 |publisher=Random House, Inc. |isbn=978-0-375-70811-4 |url-access=registration |url=https://archive.org/details/elegantuniverses0000gree }}</ref>{{rp|110}} This is an idea that contradicts our everyday experience of discrete objects. | |||
| A well-known ], which played a vital role in the history of quantum mechanics (for example, see the discussion on ]), demonstrated that if particle detectors are positioned at the slits, showing through which slit a photon goes, the interference pattern will disappear.<ref name="Feynman" /> This ''which-way'' experiment illustrates the ] principle that photons can behave as either particles or as waves, but cannot be simultaneously observed to be both a particle and a wave.<ref>{{cite web | |||
| Unexpectedly, the results discovered were that if anything is done to permit determination of which path the photon takes, the interference pattern disappears: there is '''no''' interference pattern. Each photon simply hits the detector by going through one of the two slits. Each slit yields a simple single pile of hits; there is no interference pattern. | |||
| | last = Harrison | |||
| | first = David | |||
| | title = Complementarity and the Copenhagen Interpretation of Quantum Mechanics | |||
| | work = UPSCALE | |||
| | publisher = Dept. of Physics, U. of Toronto | |||
| | year = 2002 | |||
| | url = http://www.upscale.utoronto.ca/GeneralInterest/Harrison/Complementarity/CompCopen.html | |||
| | access-date = 2008-06-21}}</ref><ref>{{cite web | |||
| | last = Cassidy | |||
| | first = David | |||
| | title = Quantum Mechanics 1925–1927: Triumph of the Copenhagen Interpretation | |||
| | work = Werner Heisenberg | |||
| | publisher = American Institute of Physics | |||
| | year = 2008 | |||
| | url = http://www.aip.org/history/heisenberg/p09.htm | |||
| | access-date = 2008-06-21 | |||
| | archive-date = 2016-01-14 | |||
| | archive-url = https://web.archive.org/web/20160114094044/https://www.aip.org/history/heisenberg/p09.htm | |||
| | url-status = dead | |||
| }}</ref><ref>{{cite conference | |||
| | first = María C. | |||
| | last = Boscá Díaz-Pintado | |||
| | title = Updating the wave-particle duality | |||
| | book-title = 15th UK and European Meeting on the Foundations of Physics | |||
| | date = 29–31 March 2007 | |||
| | location = Leeds, UK | |||
| | url = http://philsci-archive.pitt.edu/archive/00003568/ | |||
| | access-date = 2008-06-21}}</ref> | |||
| However, technically feasible realizations of this experiment were not proposed until the 1970s.<ref name=Bartell1980>{{Cite journal | last1 = Bartell | first1 = L. | title = Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behavior | doi = 10.1103/PhysRevD.21.1698 | journal = Physical Review D | volume = 21 | issue = 6 |pages=1698–1699 | year = 1980 |bibcode = 1980PhRvD..21.1698B }}</ref>{{Clarification needed|reason=What does it mean for the experiments to be feasible? Was the complementary principle not well established before the 70s?|date=February 2023}} | |||
| Which-path information and the visibility of interference fringes are complementary quantities, meaning that information about a photon's path can be observed, or interference fringes can be observed, but they cannot both be observed in the same trial. In the double-slit experiment, conventional wisdom held that observing the particles' path inevitably disturbed them enough to destroy the interference pattern as a result of the ]. | |||
| It is counterintuitive that a different outcome results based on whether or not the photon is constrained to follow one or another path well '''after''' it goes through the slit but before it hits the detector. | |||
| In 1982, Scully and Drühl pointed out a workaround alternative to this interpretation.<ref name=Scully1982>{{cite journal | first=Marlan O. | last=Scully | author-link = Marlan Scully |author2=Kai Drühl | year=1982 | journal = Physical Review A | title=Quantum eraser: A proposed photon correlation experiment concerning observation and "delayed choice" in quantum mechanics | volume = 25 | issue=4 | pages = 2208–2213 | doi=10.1103/PhysRevA.25.2208 |bibcode = 1982PhRvA..25.2208S }}</ref> They proposed to save the information about which slit the photon went through - or, in their setup, from which atom the photon was re-emitted - in the excited state of that atom. At this point the which-path information is known and no interference is observed. However, one can "erase" this information by making the atom to emit another photon and fall to the ground state. That on its own will not bring the interference pattern back, the which-path information can still be extracted from an appropriate measurement of the second photon. However, if the second photon is measured at a place where it could get to equally likely from any of the atoms, that successfully "erases" the which-path information. The original photon would now show the interference pattern (the position of its fringes depends on where exactly the second photon was observed, so that in the total statistics they average out and no fringes are seen). Since 1982, multiple experiments have demonstrated the validity of this so-called quantum "eraser".<ref name=Zajonc1991>{{cite journal |last=Zajonc |first=A. G. |author2=Wang, L. J. |author3=Zou, X. Y. |author4= Mandel, L. |title=Quantum eraser |journal=Nature |year=1991 |volume=353 |issue=6344 |pages=507–508 |bibcode = 1991Natur.353..507Z |doi = 10.1038/353507b0 |s2cid=4265543 }}</ref><ref name=Herzog1995>{{cite journal |last=Herzog |first=T. J. |author2-link=Paul Kwiat |author2=Kwiat, P. G. |author3=Weinfurter, H. |author4=Zeilinger, A. |title=Complementarity and the quantum eraser |journal=Physical Review Letters |year=1995 |volume=75 |issue=17 |pages=3034–3037 |url=http://www.ino.it/~azavatta/References/PRL753034.pdf |access-date=13 February 2014 |bibcode=1995PhRvL..75.3034H |doi=10.1103/PhysRevLett.75.3034 |pmid=10059478 |url-status=dead |archive-url=https://web.archive.org/web/20131224111021/http://www.ino.it/~azavatta/References/PRL753034.pdf |archive-date=24 December 2013 }}</ref><ref name=Walborn2002>{{cite journal | |||
| Two inconsistent accounts of the nature of light have long contended. The discovery of light's interfering with itself seemed to prove that light could not be a particle. It seemed that it had to be a wave to explain the interference seen in the double-slit experiment (first devised by ] in his classic ] of the eighteenth century). | |||
| | last =Walborn | |||
| | first =S. P. | |||
| | title =Double-Slit Quantum Eraser | |||
| | journal =Phys. Rev. A | |||
| | volume =65 | |||
| | issue =3 | |||
| | page=033818 | |||
| | year =2002 | |||
| | doi =10.1103/PhysRevA.65.033818 | |||
| | arxiv = quant-ph/0106078 | |||
| | bibcode = 2002PhRvA..65c3818W | |||
| | s2cid =55122015 | |||
| |display-authors=etal | |||
| }}</ref> | |||
| ===A simple quantum-eraser experiment=== | |||
| In the early twentieth century, experiments with the ] (the phenomenon that makes the light meters in cameras possible) gave equally strong evidence to support the idea that light is a particle phenomenon. Nothing about a photon is observable between the time it is emitted (experimenters can determine the time energy was supplied to the electron emitter) and the time it appears as the delivery of energy to some detector screen (such as a ] or the emulsion of a film camera). | |||
| A simple version of the quantum eraser can be described as follows: Rather than splitting one photon or its probability wave between two slits, the photon is subjected to a ]. If one thinks in terms of a stream of photons being randomly directed by such a beam splitter to go down two paths that are kept from interaction, it would seem that no photon can then interfere with any other or with itself. | |||
| If the rate of photon production is reduced so that only one photon enters the apparatus at any one time, it becomes impossible to understand the photon as only moving through one path, because when the path outputs are redirected so that they coincide on a common detector or detectors, interference phenomena appear. This is similar to envisioning one photon in a two-slit apparatus: even though it is one photon, it still somehow interacts with both slits. | |||
| Nevertheless, experimenters have tried to gain indirect information about which path a photon "really" takes when passing through the double-slit apparatus. | |||
| ] | |||
| In the process they learned that constraining the path taken by one of a pair of ] photons inevitably controls the path taken by the partner photon. Further, if the partner photon is sent through a double-slit device and thus interferes with itself, then very surprisingly the first photon will also behave in a way consistent with its having interfered with itself, even though there is no double-slit device in its way. | |||
| In the two diagrams in Fig. 1, photons are emitted one at a time from a laser symbolized by a yellow star. They pass through a 50% beam splitter (green block) that reflects or transmits 1/2 of the photons. The reflected or transmitted photons travel along two possible paths depicted by the red or blue lines. | |||
| In a ], one arranges to detect which one of the slits the photon passes through, and also to construct the experiment so that this information can be "erased" after the fact. | |||
| In the top diagram, it seems as though the trajectories of the photons are known: If a photon emerges from the top of the apparatus, it seems as though it had to have come by way of the blue path, and if it emerges from the side of the apparatus, it seems as though it had to have come by way of the red path. However, it is important to keep in mind that the photon is in a superposition of the paths until it is detected. The assumption above—that it 'had to have come by way of' either path—is a form of the 'separation fallacy'. | |||
| In practice, this "erasure" of path information frequently means removing the constraints that kept photons following two different paths separated from each other. | |||
| In the bottom diagram, a second beam splitter is introduced at the top right. It recombines the beams corresponding to the red and blue paths. By introducing the second beam splitter, the usual way of thinking is that the path information has been "erased." However, we have to be careful, because the photon cannot be assumed to have 'really' gone along one or the other path. Recombining the beams results in interference phenomena at detection screens positioned just beyond each exit port. What issues to the right side displays reinforcement, and what issues toward the top displays cancellation. It is important to keep in mind however that the illustrated interferometer effects apply only to a single photon in a pure state. When dealing with a pair of entangled photons, the photon encountering the interferometer will be in a mixed state, and there will be no visible interference pattern without coincidence counting to select appropriate subsets of the data.<ref>{{cite journal |last1=Jacques |first1=Vincent |last2=Wu |first2=E |last3=Grosshans |first3=Frédéric |last4=Treussart |first4=François |last5=Grangier |first5=Philippe |last6=Aspect |first6=Alain |last7=Rochl |first7=Jean-François |year=2007 |title=Experimental Realization of Wheeler's Delayed-Choice Gedanken Experiment |journal=Science |pmid=17303748 |volume=315 |issue=5814 |pages=966–968 |doi=10.1126/science.1136303 |arxiv = quant-ph/0610241 |bibcode = 2007Sci...315..966J |s2cid=6086068 }}</ref> | |||
| In one experiment, rather than splitting one photon or its probability wave between two slits, the photon is subjected to a ]. If one thinks in terms of a stream of photons being randomly directed by such a beam splitter to go down two paths that are kept from interaction, it is clear that no photon can then interfere with any other or with itself. | |||
| {{clear}} | |||
| ] | |||
| If the rate of photon production is reduced so that only one photon is entering the apparatus at any one time, however, it becomes impossible to understand the photon as only moving through one path because when their outputs are redirected so that they coincide on a common detector then interference phenomena appear. | |||
| ===Delayed choice=== | |||
| In the two diagrams to the right, photons are emitted one at a time from the yellow star. They each pass through a 50% beam splitter (green block) that reflects 1/2 of the photons, which travel along two possible paths, depicted by the red or blue lines. | |||
| Elementary precursors to current quantum-eraser experiments such as the "simple quantum eraser" described above have straightforward classical-wave explanations. Indeed, it could be argued that there is nothing particularly quantum about this experiment.<ref name=Chiao1995>{{cite journal |last=Chiao |first=R. Y. |author2=P. G. Kwiat |author3=Steinberg, A. M. |title=Quantum non-locality in two-photon experiments at Berkeley |journal=Quantum and Semiclassical Optics: Journal of the European Optical Society Part B |year=1995 |volume=7 |issue=3 |pages=259–278 |doi=10.1088/1355-5111/7/3/006|arxiv = quant-ph/9501016 |bibcode = 1995QuSOp...7..259C |s2cid=118987962 }}</ref> Nevertheless, Jordan has argued on the basis of the ], that despite the existence of classical explanations, first-order interference experiments such as the above can be interpreted as true quantum erasers.<ref name=Jordan1993>{{cite journal |last=Jordan |first=T. F. |title=Disappearance and reappearance of macroscopic quantum interference |journal=Physical Review A |year=1993 |volume=48 |issue=3 |pages=2449–2450 |bibcode = 1993PhRvA..48.2449J |doi = 10.1103/PhysRevA.48.2449 |pmid=9909872 }}</ref> | |||
| These precursors use single-photon interference. Versions of the quantum eraser using entangled photons, however, are intrinsically non-classical. Because of that, in order to avoid any possible ambiguity concerning the quantum versus classical interpretation, most experimenters have opted to use nonclassical entangled-photon light sources to demonstrate quantum erasers with no classical analog. | |||
| In the top diagram, one can see that the trajectories of photons are clearly known — in the sense that if a photon emerges at the top of the apparatus it appears that it had to have come by the path that leads to that point (blue line) and if it emerges at the side of the apparatus it appears that it had to have come by way of the other path (red line). | |||
| Furthermore, the use of entangled photons enables the design and implementation of versions of the quantum eraser that are impossible to achieve with single-photon interference, such as the '''delayed-choice quantum eraser''', which is the topic of this article. | |||
| Next, as shown in the bottom diagram, a second beam splitter is introduced at the top right. It can direct either beam towards either path; thus note that whatever emerges from each exit port may have come by way of either path. | |||
| ==The experiment of Kim ''et al.'' (1999)== | |||
| It is in this sense that the path information has been "erased". | |||
| Note that total phase differences are introduced along the two paths because of the different effects of passing through a glass plate, being reflected off its first surface, or passing through the back surface of a semi-silvered beam splitter and being reflected by the back (inner side) of the reflective surface. | |||
| The result is that waves pass out of both the top upwards exit, and also the top-right exit. Specifically, waves passing out the top exit interfere destructively, whereas waves passing out the upper right side exit interfere constructively. | |||
| A more detailed explanation of the phase changes involved here can be found in the ] article. Also, the experiment depicted above is reported in full in a reference.<ref>{{cite journal |last1=Jacques |first1=Vincent |last2=Wu |first2=E |last3=Grosshans|first3=Frédéric|last4=Treussart|first4=François|last5=Grangier|first5=Philippe|last6=Aspect|first6=Alain|last7=Rochl|first7=Jean-François|year=2007 |title=Experimental Realization of Wheeler's Delayed-Choice Gedanken Experiment |journal=Science |publisher= |pmid=17303748|volume=315 |issue=5814 |pages=pp. 966–968 |url=http://www.sciencemag.org/cgi/content/full/315/5814/966 |doi=10.1126/science.1136303 |arxiv = quant-ph/0610241 |bibcode = 2007Sci...315..966J }}</ref> | |||
| If the second beam splitter in the lower diagram could be inserted or removed one might assert that a photon must have traveled by way of one path or the other if a photon were detected at the end of one path or the other. The appearance would be that the photon "chose" one path or the other at the only (bottom left) beam splitter, and therefore could only arrive at the respective path end. | |||
| The subjective assurance that the photon followed a single path is brought into question, however, if (after the photon has presumably "decided" which path to take) a second beam splitter then makes it impossible to say by which path the photon has traveled. | |||
| What once appeared to be a black and white issue now appears to be a "gray" issue. It is the mixture of two originally separated paths that constitutes what is colloquially referred to as "erasure." It is actually more like "a return to indeterminability." | |||
| ==The experiment== | |||
| {{clear}} | {{clear}} | ||
| ] | ] | ||
| The experimental setup, described in detail in |
The experimental setup, described in detail in Kim ''et al.'',<ref name="DCQE" /> is illustrated in Fig 2. An argon laser generates individual 351.1 nm photons that pass through a double-slit apparatus (vertical black line in the upper left corner of the diagram). | ||
| An individual photon goes through one (or both) of the two slits. In the illustration, the photon paths are color-coded as red or light blue lines to indicate which slit the photon came through (red indicates slit A, light blue indicates slit B). | |||
| So far, the experiment is like a conventional two-slit experiment. However, after the slits |
So far, the experiment is like a conventional two-slit experiment. However, after the slits, ] (SPDC) is used to prepare an entangled two-photon state. This is done by a nonlinear optical crystal BBO (]) that converts the photon (from either slit) into two identical, orthogonally polarized entangled photons with 1/2 the frequency of the original photon. The paths followed by these orthogonally polarized photons are caused to diverge by the ]. | ||
| One of these photons, referred to as the "signal" photon (look at the red and light-blue lines going ''upwards'' from the |
One of these 702.2 nm photons, referred to as the "signal" photon (look at the red and light-blue lines going ''upwards'' from the Glan–Thompson prism) continues to the target detector called ''D''<sub>0</sub>. During an experiment, detector ''D''<sub>0</sub> is scanned along its ''x'' axis, its motions controlled by a step motor. A plot of "signal" photon counts detected by ''D''<sub>0</sub> versus ''x'' can be examined to discover whether the cumulative signal forms an interference pattern. | ||
| The other entangled photon, referred to as the "idler" photon (look at the red and light-blue lines going ''downwards'' from the |
The other entangled photon, referred to as the "idler" photon (look at the red and light-blue lines going ''downwards'' from the Glan–Thompson prism), is deflected by prism ''PS'' that sends it along divergent paths depending on whether it came from slit ''A'' or slit ''B''. | ||
| Somewhat beyond the path split ]s |
Somewhat beyond the path split, the idler photons encounter ]s ''BS''<sub>a</sub>, ''BS''<sub>b</sub>, and ''BS''<sub>c</sub> that each have a 50% chance of allowing the idler photon to pass through and a 50% chance of causing it to be reflected. ''M''<sub>a</sub> and ''M''<sub>b</sub> are mirrors. | ||
| ] | |||
| Because of the way the beam splitters are arranged the idler can be detected by detectors labeled D<sub>1</sub>, D<sub>2</sub>, D<sub>3</sub> and D<sub>4</sub>. Note that: | |||
| ] | |||
| The beam splitters and mirrors direct the idler photons towards detectors labeled ''D''<sub>1</sub>, ''D''<sub>2</sub>, ''D''<sub>3</sub> and ''D''<sub>4</sub>. Note that: | |||
| * If an idler photon is recorded at detector ''D''<sub>3</sub>, it can only have come from slit B. | |||
| * If an idler photon is recorded at detector ''D''<sub>4</sub>, it can only have come from slit A. | |||
| * If an idler photon is detected at detector ''D''<sub>1</sub> or ''D''<sub>2</sub>, it might have come from slit A or slit B. | |||
| * The optical path length measured from slit to ''D''<sub>1</sub>, ''D''<sub>2</sub>, ''D''<sub>3</sub>, and ''D''<sub>4</sub> is 2.5 m longer than the optical path length from slit to ''D''<sub>0</sub>. This means that any information that one can learn from an idler photon must be approximately 8 ns later than what one can learn from its entangled signal photon. | |||
| Detection of the idler photon by ''D''<sub>3</sub> or ''D''<sub>4</sub> provides delayed "which-path information" indicating whether the signal photon with which it is entangled had gone through slit A or B. On the other hand, detection of the idler photon by ''D''<sub>1</sub> or ''D''<sub>2</sub> provides a delayed indication that such information is not available for its entangled signal photon. Insofar as which-path information had earlier potentially been available from the idler photon, it is said that the information has been subjected to a "delayed erasure". | |||
| If it is recorded at detector D<sub>3</sub>, then it can only have come from slit B. | |||
| By using a ], the experimenters were able to isolate the entangled signal from photo-noise, recording only events where both signal and idler photons were detected (after compensating for the 8 ns delay). Refer to Figs 3 and 4. | |||
| If it is recorded at detector D<sub>4</sub> it can only have come from slit A. | |||
| * When the experimenters looked at the signal photons whose entangled idlers were detected at ''D''<sub>1</sub> or ''D''<sub>2</sub>, they detected interference patterns. | |||
| * However, when they looked at the signal photons whose entangled idlers were detected at ''D''<sub>3</sub> or ''D''<sub>4</sub>, they detected simple diffraction patterns with no interference. | |||
| ===Significance=== | |||
| If the idler is detected at detector D<sub>1</sub> or D<sub>2</sub>, it might have come from ''either'' slit (A or B). | |||
| This result is similar to that of the double-slit experiment since interference is observed when it is extracted according to phase value (R<sub>01</sub> or R<sub>02</sub>). | |||
| Note that the phase cannot be measured if the photon's path (the slit through which it passes) is known. | |||
| ]. When all the bulbs are lit, billboard does not reveal any pattern of image, which can be "recovered" only by switching off some bulbs. Likewise interference pattern or no-interference pattern among signal photons at ''D''<sub>0</sub> can be recovered only after "switching off" (or ignoring) some signal photons and which signal photons should be ignored to recover pattern, this information can be gained only by looking at corresponding entangled idler photons in detectors ''D''<sub>1</sub> to ''D''<sub>4</sub>.]] | |||
| Thus, which detector receives the idler photon either gives information as to whether the signal photon with which it is entangled went through slit A or B ("which-path information"), or implies that such information is not available (from this source). Insofar as which-path information was potentially available from the idler photon earlier, it is said that the information has been "erased". | |||
| However, what makes this experiment possibly astonishing is that, unlike in the classic double-slit experiment, the choice of whether to preserve or erase the which-path information of the idler was not made until 8 ns ''after'' the position of the signal photon had already been measured by ''D''<sub>0</sub>. | |||
| By using a ] the experimenters were able to isolate the entangled signal from the overwhelming photo-noise of the laboratory, recording only events where both signal and idler photons were detected. | |||
| Detection of signal photons at ''D''<sub>0</sub> does not directly yield any which-path information. Detection of idler photons at ''D''<sub>3</sub> or ''D''<sub>4</sub>, which provide which-path information, means that no interference pattern can be observed in the jointly detected subset of signal photons at ''D''<sub>0</sub>. Likewise, detection of idler photons at ''D''<sub>1</sub> or ''D''<sub>2</sub>, which do not provide which-path information, means that interference patterns ''can'' be observed in the jointly detected subset of signal photons at ''D''<sub>0</sub>. | |||
| When the experimenters ''looked only at'' the signal photons whose entangled idlers were detected at D<sub>1</sub> or D<sub>2</sub>, they found an interference pattern. | |||
| In other words, even though an idler photon is not observed until long after its entangled signal photon arrives at ''D''<sub>0</sub> due to the shorter optical path for the latter, interference at ''D''<sub>0</sub> is determined by whether a signal photon's entangled idler photon is detected at a detector that preserves its which-path information (''D''<sub>3</sub> or ''D''<sub>4</sub>), or at a detector that erases its which-path information (''D''<sub>1</sub> or ''D''<sub>2</sub>). | |||
| However, when they looked at the signal photons whose entangled idlers were detected at D<sub>3</sub> or similarly at D<sub>4</sub>, ''they found no interference''. | |||
| Some have interpreted this result to mean that the delayed choice to observe or not observe the path of the idler photon changes the outcome of an event in the past.<ref name=Ionicioiu2011>{{cite journal |last=Ionicioiu |first=R. |author2=Terno, D. R. |title=Proposal for a quantum delayed-choice experiment |journal=Phys. Rev. Lett. |year=2011 |volume=107 |issue=23|page=230406 |doi=10.1103/physrevlett.107.230406 |arxiv = 1103.0117 |bibcode = 2011PhRvL.107w0406I |pmid=22182073|s2cid=44297197 }}</ref>{{Better source needed|reason=There it says nothing about what the consensus is.|date=October 2015}}<ref>J.A. Wheeler, Quantum Theory and Measurement, Princeton University Press p.192-213</ref> Note in particular that an interference pattern may only be pulled out for observation ''after'' the idlers have been detected (i.e., at ''D''<sub>1</sub> or ''D''<sub>2</sub>).{{clarify|date=October 2015}} | |||
| This result is similar to that of the double-slit experiment since interference is observed when it is not known which slit the photon went through, while no interference is observed when the path is known. | |||
| The total pattern of all signal photons at ''D''<sub>0</sub>, whose entangled idlers went to multiple different detectors, will never show interference regardless of what happens to the idler photons.<ref name="Greene">{{cite book | last = Greene | first = Brian | author-link = Brian Greene | title = The Fabric of the Cosmos: Space, Time, and the Texture of Reality | publisher = Alfred A. Knopf | year = 2004 | isbn = 978-0-375-41288-2 | page = | title-link = The Fabric of the Cosmos: Space, Time, and the Texture of Reality }}</ref> One can get an idea of how this works by looking at the graphs of ''R''<sub>01</sub>, ''R''<sub>02</sub>, ''R''<sub>03</sub>, and ''R''<sub>04</sub>, and observing that the peaks of ''R''<sub>01</sub> line up with the troughs of ''R''<sub>02</sub> (i.e. a π phase shift exists between the two interference fringes). ''R''<sub>03</sub> shows a single maximum, and ''R''<sub>04</sub>, which is experimentally identical to ''R''<sub>03</sub> will show equivalent results. The entangled photons, as filtered with the help of the coincidence counter, are simulated in Fig. 5 to give a visual impression of the evidence available from the experiment. In D<sub>0</sub>, the sum of all the correlated counts will not show interference. If all the photons that arrive at ''D''<sub>0</sub> were to be plotted on one graph, one would see only a bright central band. | |||
| However, what makes this experiment possibly astonishing is that, unlike in the classic double-slit experiment, the choice of whether to preserve or erase the which-path information of the idler need not be made until ''after'' the position of the signal photon has already been measured by D<sub>0</sub>. | |||
| ==Implications== | |||
| There is never any which-path information determined directly for the photons that are detected at D<sub>0</sub>, yet detection of which-path information by D<sub>3</sub> or D<sub>4</sub> means that no interference pattern is observed in the corresponding subset of signal photons at D<sub>0</sub>. | |||
| === Retrocausality === | |||
| The results from Kim, et al.<ref name="DCQE" /> have shown that whether the idler photon is detected at a detector that preserves its which-path information (D<sub>3</sub> or D<sub>4</sub>) or a detector that erases its which-path information (D<sub>1</sub> or D<sub>2</sub>) determines whether interference is seen at D<sub>0</sub>, even though the idler photon ''is not observed until after'' the signal photon arrives at D<sub>0</sub> due to the shorter optical path for the latter. | |||
| ]s raise questions about the causal connections between the events.<ref group=note>Stanford Encyclopedia of Philosophy, "More recently, the Bell-type experiments have been interpreted by some as if quantum events could be connected in such a way that the past light cone might be accessible under non-local interaction; not only in the sense of action at a distance but as backward causation. One of the most enticing experiments of this kind is the Delayed Choice Quantum Eraser designed by Yoon-Ho Kim et al. (2000). It is a rather complicated construction. It is set up to measure correlated pairs of photons, which are in an entangled state so that one of the two photons is detected 8 nanoseconds before its partner. The results of the experiment are quite amazing. They seem to indicate that the behavior of the photons detected these 8 nanoseconds before their partners is determined by how the partners will be detected. Indeed it might be tempting to interpret these results as an example of the future causing the past. The result is, however, in accordance with the predictions of quantum mechanics." http://plato.stanford.edu/entries/causation-backwards/.</ref> If events at ''D''<sub>1</sub>, ''D''<sub>2</sub>, ''D''<sub>3</sub>, ''D''<sub>4</sub> determine outcomes at ''D''<sub>0</sub>, then the effects might seem to precede their causes in time. | |||
| === Consensus: no retrocausality === | |||
| Some have interpreted this result to mean that the delayed choice to observe or not observe the path of the idler photon will change the outcome of an event in the past. However, an interference pattern may only be observed ''after'' the idlers have been detected (i.e., at D<sub>1</sub> or D<sub>2</sub>). | |||
| However, the interference pattern can only be seen retroactively once the idler photons have been detected and the detection information used to select subsets of signal photons.<ref name=Greene2004>{{cite book |last=Greene |first=Brian |title=The Fabric of the Cosmos |url=https://archive.org/details/fabricofcosmossp00gree |url-access=registration |year=2004 |publisher=Alfred A. Knopf |isbn=978-0-375-41288-2}}</ref>{{rp|197}} | |||
| Moreover, it's observed that the apparent retroactive action vanishes if the effects of observations on the state of the ] signal and idler photons are considered in their historic order. Specifically, in the case when detection/deletion of which-way information happens ''before'' the detection on ''D''<sub>0</sub>, the standard simplistic explanation says "The detector ''D''<sub>i</sub>, at which the idler photon is detected, determines the probability distribution at ''D''<sub>0</sub> for the signal photon". Similarly, in the case when ''D''<sub>0</sub> ''precedes'' detection of the idler photon, the following description is just as accurate: "The position at ''D''<sub>0</sub> of the detected signal photon determines the probabilities for the idler photon to hit either of ''D''<sub>1</sub>, ''D''<sub>2</sub>, ''D''<sub>3</sub> or ''D''<sub>4</sub>". These are just equivalent ways of formulating the correlations of entangled photons' observables in an intuitive causal way, so one may choose any of those (in particular, that one where the cause precedes the consequence and no retrograde action appears in the explanation). | |||
| Note that the total pattern of all signal photons at D<sub>0</sub>, whose entangled idlers went to multiple different detectors, will never show interference regardless of what happens to the idler photons.<ref name="Greene">{{cite book | last = Greene | first = Brian | authorlink = Brian Greene | title = The Fabric of the Cosmos | publisher = Alfred A. Knopf | year = 2004 | isbn = 0-375-41288-3 | page = 198}}</ref> One can get an idea of how this works by looking carefully at both the graph of the subset of signal photons whose idlers went to detector D<sub>1</sub> (fig. 3 in the paper<ref name="DCQE" />), and the graph of the subset of signal photons whose idlers went to detector D<sub>2</sub> (fig. 4), and observing that the peaks of the first interference pattern line up with the troughs of the second and vice versa (noted in the paper as "a π phase shift between the two interference fringes"), so that the sum of the two will not show interference. | |||
| The total pattern of signal photons at the primary detector never shows interference (see Fig. 5), so ''it is not possible to deduce what will happen to the idler photons by observing the signal photons alone''. In a paper by Johannes Fankhauser, it is shown that the delayed choice quantum eraser experiment resembles a Bell-type scenario in which the paradox's resolution is rather trivial, and so there really is no mystery. Moreover, it gives a detailed account of the experiment in the de Broglie-Bohm picture with definite trajectories arriving at the conclusion that there is no "backwards in time influence" present.<ref>{{cite journal |arxiv=1707.07884|doi=10.12743/quanta.v8i1.88|title=Taming the Delayed Choice Quantum Eraser|year=2019|last1=Fankhauser|first1=Johannes|journal=Quanta|volume=8|pages=44–56|s2cid=53574007}}</ref> The delayed-choice quantum eraser does not communicate information in a retro-causal manner because it takes another signal, one which must arrive by a process that can go no faster than the speed of light, to sort the superimposed data in the signal photons into four streams that reflect the states of the idler photons at their four distinct detection screens.<ref group=note>"... the future measurements do not in any way change the data you collected today. But the future measurements ''do'' influence the kinds of details you can invoke when you subsequently describe what happened today. Before you have the results of the idler photon measurements, you really can't say anything at all about the which-path history of any given signal photon. However, once you have the results, you conclude that signal photons whose idler partners were successfully used to ascertain which-path information ''can'' be described as having ... traveled either left or right. You also conclude that signal photons whose idler partners had their which-path information erased ''cannot'' be described as having ... definitely gone one way or the other (a conclusion you can convincingly confirm by using the newly acquired idler photon data to expose the previously hidden interference pattern among this latter class of signal photons). We thus see that the future helps shape the story you tell of the past." — Brian Greene, '']'', ''pp'' 198–199</ref><ref group=note>The Kim paper says: '''P. 1f:''' The experiment is designed in such a way that L0, the optical distance between atoms A, B and detector D<sub>0</sub>, is much shorter than Li, which is the optical distance between atoms A, B and detectors D<sub>1</sub>, D<sub>2</sub>, D<sub>3</sub>, and D<sub>4</sub>, respectively. So that D<sub>0</sub> will be triggered much earlier by photon 1. After the registration of photon 1, we look at these "delayed" detection events of D<sub>1</sub>, D<sub>2</sub>, D<sub>3</sub>, and D<sub>4</sub> which have constant time delays, i ≃ (Li − L0)/c, relative to the triggering time of D<sub>0</sub>. | |||
| === Explanation by physical optics === | |||
| '''P.2:''' In this experiment the optical delay (Li − L0) is chosen to be ≃ 2.5m, where L0 is the optical distance between the output surface of BBO and detector D<sub>0</sub>, and Li is the optical distance between the output surface of the BBO and detectors D<sub>1</sub>, D<sub>2</sub>, D<sub>3</sub>, and D<sub>4</sub>, respectively. This means that any information one can learn from photon 2 must be at least 8ns later than what one has learned from the registration of photon 1. Compared to the 1ns response time of the detectors, 2.5m delay is good enough for a "delayed erasure". | |||
| By examining the positions of signal photons at detector D<sub>0</sub>, which correspond to idler photons at D<sub>1</sub> or D<sub>2</sub>, an interference pattern is found in the recorded data. There seems to be a misconception, where this pattern originates from. One might think, the signal photons shape the pattern on the way to detector D<sub>0</sub> by interfering with each other. But at detector D<sub>0</sub> only a blurred image of the double slit is projected by the converging lens, effectively smearing any direct interference patterns from the slits. | |||
| '''P. 3:''' The which-path or both-path information of a quantum can be erased or marked by its entangled twin even after the registration of the quantum. | |||
| To understand the source of the derived interference pattern, one has to focus on the third beam splitter BS<sub>C</sub>, where the photon paths from both slits merge. At this point a phase difference exists between the merging paths, which is dependent on the different path lengths from slit A or B respectively to the splitter. Furthermore path length and phase difference depend in part on the deviation angle of the idler photon leaving the Glan-Thompson prism. While a fixed position on detector D<sub>0</sub> is correlated to events at detector D<sub>1</sub> or D<sub>2</sub>, only events at D<sub>1</sub> or D<sub>2</sub> are inspected, which share the same phase differences. After leaving the beam splitter BS<sub>C</sub>, each phase difference may lead to constructive or destructive interference on the paths from the splitter to the detectors D<sub>1</sub> and D<sub>2</sub>, while also allowing any arbitrary intermediate values. But one has to note, that the combined probabilities for both paths behind BS<sub>C</sub> always add up to 1, as the difference of the phase shifts between that paths amounts to π or 180°. | |||
| '''P. 2:''' After the registration of photon 1, we look at these "delayed" detection events of D<sub>1</sub>, D<sub>2</sub>, D<sub>3</sub>, and D<sub>4</sub> which have constant time delays, i ≃ (Li − L0)/c, relative to the triggering time of D<sub>0</sub>. '''It is easy to see these "joint detection" events must have resulted from the same photon pair.''' (Emphasis added. This is the point at which what is going on at D<sub>0</sub> can be figured out.) | |||
| By changing the detector D<sub>0</sub> position, different phase shifts at detector D<sub>1</sub> and D<sub>2</sub> lead to a different statistic in observed correlated events: A derived interference pattern builds up in the data. Consequently the derived patterns from detectors D<sub>1</sub> and D<sub>2</sub> add up to the Gaussian distribution, which is observed with the detectors D<sub>3</sub> and D<sub>4</sub>. | |||
| </ref> | |||
| A theorem proven by Phillippe Eberhard shows that if the accepted equations of ] are correct, faster than light communications is impossible.<ref>{{cite journal | last = Eberhard | first = Phillippe H. |author2=Ronald R. Ross | title = Quantum field theory cannot provide faster-than-light communication | journal = Foundations of Physics Letters | volume = 2 | issue = 2 | pages =127–149 | year = 1989 | doi = 10.1007/BF00696109 | bibcode=1989FoPhL...2..127E| s2cid = 123217211 | url = https://escholarship.org/content/qt5604n7md/qt5604n7md.pdf?t=p0fuo8 }}</ref> (See reference<ref>{{cite arXiv |eprint=1007.3977|last1=Gaasbeek|first1=Bram|title=Demystifying the Delayed Choice Experiments|class=quant-ph|year=2010}}</ref> for a treatment emphasizing the role of conditional probabilities.) | |||
| Data from events correlated with photons at detectors D<sub>3</sub> and D<sub>4</sub> show no derived interference patterns, because there is no interference of different photon paths from both slits in the first place. | |||
| ==Other delayed-choice quantum-eraser experiments== | |||
| === Time relations among data === | |||
| {{expand section|date=February 2014}} | |||
| ] | |||
| ] By noting which photons reaching Detector 0 correspond with photons reaching Detectors 1, 2, 3, and 4, it is possible to sort photon records collected by Detector 0 into four groups. Only then will it become possible to see interference patterns in two groups and only diffraction patterns in the other two groups. If there were no coincidence counter, then there would be no way to distinguish any photon that arrives at Detector 0 from any other photon that reaches it. | |||
| Many refinements and extensions of Kim ''et al.'' delayed-choice quantum eraser have been performed or proposed. Only a small sampling of reports and proposals are given here: | |||
| Photons will not reach detectors one through four in regular rotation, so the only way to sort out the photons that are entangled twins with the ones that reached each of those detectors is to group them according to which of those four detectors was activated when a photon reached Detector 0. Note that in the schematic diagrams the fringes or interference patterns imaged by Detector 1 and Detector 2 will add together to form a solid band. The addition of the diffraction patterns paired with the diffraction patterns seen by Detector 3 and Detector 4 will make the center area somewhat brighter than it would otherwise be, but would have no other influence on the confused picture produced by the raw data gathered at Detector 0. | |||
| Scarcelli ''et al.'' (2007) reported on a delayed-choice quantum-eraser experiment based on a two-photon imaging scheme. After detecting a photon passed through a double-slit, a random delayed choice was made to erase or not erase the which-path information by the measurement of its distant entangled twin; the particle-like and wave-like behavior of the photon were then recorded simultaneously and respectively by only one set of joint detectors.<ref name=Scarcelli2007>{{cite journal |last=Scarcelli |first=G. |author2=Zhou, Y. |author3=Shih, Y. |title=Random delayed-choice quantum eraser via two-photon imaging |journal=The European Physical Journal D |year=2007 |volume=44 |issue=1 |pages=167–173 |arxiv=quant-ph/0512207 |bibcode = 2007EPJD...44..167S |doi = 10.1140/epjd/e2007-00164-y |s2cid=10267634 }}</ref> | |||
| It is impossible to know which group a photon appearing at Detector 0 at time T<sub>1</sub> may belong to until '''after''' its entangled partner is found at one of the other detectors and their coincidence is measured at some slightly later time T<sub>2</sub>. | |||
| Peruzzo ''et al.'' (2012) have reported on a quantum delayed-choice experiment based on a quantum-controlled beam splitter, in which particle and wave behaviors were investigated simultaneously. The quantum nature of the photon's behavior was tested with a Bell inequality, which replaced the delayed choice of the observer.<ref name=Peruzzo2012>{{cite journal |last=Peruzzo |first=A. |author2=Shadbolt, P. |author3=Brunner, N. |author4=Popescu, S. |author5= O'Brien, J. L. |title=A quantum delayed-choice experiment |journal=Science |year=2012 |volume=338 |issue=6107|pages=634–637 |arxiv = 1205.4926 |bibcode = 2012Sci...338..634P |doi = 10.1126/science.1226719 |pmid=23118183|s2cid=3725159 }}</ref> | |||
| ==Discussion== | |||
| Rezai ''et al.'' (2018) have combined the ] with a delayed choice quantum eraser. They impose two incompatible photons onto a beam-splitter, such that no interference pattern could be observed. When the output ports are monitored in an integrated fashion (i.e. counting all the clicks), no interference occurs. Only when the outcoming photons are polarization analysed and the right subset is selected, quantum interference in the form of a ] occurs.<ref name=Rezai2018>{{cite journal |last=Rezai |first=M. |author2=Wrachtrup, J. |author3=Gerhardt, I. |title=Coherence Properties of Molecular Single Photons for Quantum Networks |journal=Physical Review X |year=2018 |volume=8|issue=3|pages=031026|doi=10.1103/PhysRevX.8.031026|bibcode=2018PhRvX...8c1026R |doi-access=free }}</ref> | |||
| === Problems with using retrocausality === | |||
| {{Unreferenced section|date=August 2012|reason=This section is a nice and clear description of the problem with retrocausality, however, without any reference to the source there is no way of getting a deeper background on the explanation}} | |||
| This delayed choice quantum eraser experiment raises questions about time, time sequences, and thereby brings our usual ideas of time and causal sequence into question. If a determining factor in the complicated (lower) part of the apparatus determines an outcome in the simple part of the apparatus that consists of only a lens and a detection screen, then effect seems to precede cause. So if the light paths involved in the complicated part of the apparatus were greatly extended in order that, e.g., a year might go by before a photon showed up at D<sub>1</sub>, D<sub>2</sub>, D<sub>3</sub>, or D<sub>4</sub>, then when a photon showed up in one of these detectors it would cause the photon in the upper, simple part of the apparatus to have shown up in a certain mode a year earlier. Perhaps by re-routing light paths to the four detectors during that one year so that the number of possible outcomes is reduced to two or even perhaps to one, then the experimenter could send a signal back through time. Changing between the first possible arrangement and second possible arrangement of parts in the complicated part of the experiment would then function like the opening and closing of a telegraph key. | |||
| The construction of solid-state electronic ]s (MZI) has led to proposals to use them in electronic versions of quantum-eraser experiments. This would be achieved by Coulomb coupling to a second electronic MZI acting as a detector.<ref name=Dressel2012>{{cite journal |last=Dressel |first=J. |author2=Choi, Y. |author3=Jordan, A. N. |title=Measuring which-path information with coupled electronic Mach-Zehnder interferometers |journal=Physical Review B |year=2012 |volume=85 |issue=4 |page=045320 |arxiv=1105.2587|doi=10.1103/physrevb.85.045320|s2cid=110142737 }}</ref> | |||
| === Details pertaining to retrocausality in the Kim experiment === | |||
| Entangled pairs of neutral ]s have also been examined and found suitable for investigations using quantum marking and quantum-erasure techniques.<ref name=Bramon2004>{{cite journal |last=Bramon |first=A. |author2=Garbarino, G. |author3=Hiesmayr, B. C.|author3-link=Beatrix Hiesmayr |title=Quantum marking and quantum erasure for neutral kaons |journal=Physical Review Letters |year=2004 |volume=92 |issue=2 |page=020405 |doi=10.1103/physrevlett.92.020405 |arxiv = quant-ph/0306114 |bibcode = 2004PhRvL..92b0405B |pmid=14753924|s2cid=36478919 }}</ref> | |||
| In their paper, Kim, et al.<ref name="DCQE" /> explain that the concept of ] is one of the most basic principles of quantum mechanics. According to the ], it is not possible to precisely measure both the position and the momentum of a quantum particle at the same time. In other words, position and momentum are ''complementary''. In 1927, ] maintained that quantum particles have both "wave-like" behavior and "particle-like" behavior, but can exhibit only one kind of behavior under conditions that prevent exhibiting the complementary characteristics. This complementarity has come to be known as the ] of quantum mechanics. ] believed that the presence of these two aspects under conditions that prevent their simultaneous manifestation is the basic mystery of quantum mechanics. | |||
| A quantum eraser has been proposed using a modified ] setup. In this proposal, no coincident counting is required, and quantum erasure is accomplished by applying an additional Stern-Gerlach magnetic field.<ref name=Qureshi2012>{{cite journal |last=Qureshi |first=T. |author2=Rahman, Z. |title=Quantum eraser using a modified Stern-Gerlach setup |journal=Progress of Theoretical Physics |year=2012 |volume=127|issue=1 |pages=71–78 |doi=10.1143/PTP.127.71 |arxiv = quant-ph/0501010 |bibcode=2012PThPh.127...71Q |s2cid=59470770 }}</ref> | |||
| According to Kim, et al., "The actual mechanisms that enforce complementarity vary from one experimental situation to another."<ref name="DCQE" /> In the double-slit experiment, the common wisdom is that complementarity makes it seemingly impossible to determine which slit the photon passes through without at the same time disturbing it enough to destroy the interference pattern. A 1982 paper by Scully and ] circumvented the issue of disturbance due to direct measurement of the photon,<ref name="scullydruhl">{{cite journal | first=Marlan O. | last=Scully | authorlink = Marlan Scully | coauthors = Kai Drühl | year=1982 | journal = ] A | title=Quantum eraser: A proposed photon correlation experiment concerning observation and "delayed choice" in quantum mechanics | volume = 25 | issue=4 | pages = 2208–2213 | doi=10.1103/PhysRevA.25.2208 |bibcode = 1982PhRvA..25.2208S }}</ref> according to Kim, et al. Scully and Drühl "found a way around the position-momentum uncertainty obstacle and proposed a quantum eraser to obtain which-path or particle-like information without introducing large uncontrolled phase factors to disturb the interference."<ref name="DCQE" /> | |||
| == Notes == | |||
| Scully and Drühl found that there is no interference pattern when which-path information is obtained, even if this information was obtained without directly observing the original photon, but that if you somehow "erase" the which-path information, an interference pattern is again observed. | |||
| {{Reflist|group=note}} | |||
| In the delayed choice quantum eraser discussed here, the pattern exists even if the which-path information is erased shortly later in time than the signal photons hit the primary detector. However, the interference pattern can only be seen retroactively once the idler photons have already been detected and the experimenter has obtained information about them, with the interference pattern being seen when the experimenter looks at particular ''subsets'' of signal photons that were matched with idlers that went to particular detectors. | |||
| === The main stumbling block for using retrocausality to communicate information === | |||
| The total pattern of signal photons at the primary detector never shows interference, so it is not possible to deduce what will happen to the idler photons by observing the signal photons alone, which would open up the possibility of gaining information ] (since one might deduce this information before there had been time for a message moving at the speed of light to travel from the idler detector to the signal photon detector) or even gaining information about the future (since as noted above, the signal photons may be detected at an earlier time than the idlers), both of which would qualify as violations of ] in physics. The apparatus under discussion here could not communicate information in a retro-causal manner because it takes another signal, one which must arrive via a process that can go no faster than the speed of light, to sort the superimposed data in the signal photons into four streams that reflect the states of the idler photons at their four distinct detection screens. {{citation needed|date=August 2012}} | |||
| In fact, a theorem proved by Phillippe Eberhard shows that if the accepted equations of ] are correct, it should never be possible to experimentally violate causality using quantum effects<ref>{{cite journal | last = Eberhard | first = Phillippe H. | coauthors = Ronald R. Ross | title = Quantum field theory cannot provide faster-than-light communication | journal = Foundations of Physics Letters | volume = 2 | issue = 2 | pages = p. 127–149 | year = 1989 | url = http://www.springerlink.com/content/g7w8441j75831k4x/ | doi = 10.1007/BF00696109 | bibcode=1989FoPhL...2..127E}}</ref> (see reference<ref>Bram Gaasbeek. . ] preprint, 22 July 2010.</ref> for a treatment emphasizing the role of conditional probabilities). | |||
| === Yet there are those who persevere in attempting to communicate retroactively === | |||
| Some physicists have speculated about the possibility that these experiments might be changed in a way that would be consistent with previous experiments, yet which could allow for experimental causality violations.<ref>]. . "Alternate View" column, ], February 1995.</ref><ref>], Ludmila Dolmatova. . ] preprint, 7 August 2000.</ref> | |||
| ==See also== | |||
| *] | |||
| *] | |||
| *The ] of quantum mechanics | |||
| *] | |||
| *] | |||
| *] | |||
| ==References== | ==References== | ||
| {{reflist|30em}} | |||
| <references /> | |||
| ==External links== | ==External links== | ||
| * | * | ||
| * | |||
| * | |||
| * | * | ||
| * {{cite journal |arxiv=quant-ph/0009097 |doi=10.1140/epjd/e20020030|bibcode=2002EPJD...18..251T|title=Comprehensive experimental test of quantum erasure|year=2002|last1=Trifonov|first1=A.|last2=Björk|first2=G.|last3=Söderholm|first3=J.|last4=Tsegaye|first4=T.|journal=The European Physical Journal D |volume=18|issue=2|pages=251–258|s2cid=119026478}} | |||
| * | |||
| * {{cite journal |arxiv=1206.6578|doi=10.1073/pnas.1213201110|pmid=23288900|pmc=3557028|bibcode=2013PNAS..110.1221M|title=Quantum erasure with causally disconnected choice|year=2013|last1=Ma|first1=Xiao-Song|last2=Kofler|first2=Johannes|last3=Qarry|first3=Angie|last4=Tetik|first4=Nuray|last5=Scheidl|first5=Thomas|last6=Ursin|first6=Rupert|last7=Ramelow|first7=Sven|last8=Herbst|first8=Thomas|last9=Ratschbacher|first9=Lothar|last10=Fedrizzi|first10=Alessandro|last11=Jennewein|first11=Thomas|last12=Zeilinger|first12=Anton|journal=Proceedings of the National Academy of Sciences|volume=110|issue=4|pages=1221–1226|doi-access=free}} | |||
| * ({{doi|10.1140/epjd/e20020030}}) | |||
| * , YouTube (with an explanation of the experiment by Kim et al. in minutes 3:31 to 9:09) | |||
| * ]) ] | |||
| * {{cite journal |arxiv=1707.07884|doi=10.12743/quanta.v8i1.88|title=Taming the Delayed Choice Quantum Eraser|year=2019|last1=Fankhauser|first1=Johannes|journal=Quanta|volume=8|pages=44–56|s2cid=53574007}} | |||
| {{Quantum mechanics topics}} | |||
| {{DEFAULTSORT:Delayed Choice Quantum Eraser}} | {{DEFAULTSORT:Delayed Choice Quantum Eraser}} | ||
Latest revision as of 17:59, 21 November 2024
Physics experiment in quantum mechanics| Part of a series of articles about |
| Quantum mechanics |
|---|
| Schrödinger equation |
| Background |
| Fundamentals |
| Experiments |
| Formulations |
| Equations |
| Interpretations |
| Advanced topics |
Scientists
|
A delayed-choice quantum eraser experiment, first performed by Yoon-Ho Kim, R. Yu, S. P. Kulik, Y. H. Shih and Marlan O. Scully, and reported in early 1998, is an elaboration on the quantum eraser experiment that incorporates concepts considered in John Archibald Wheeler's delayed-choice experiment. The experiment was designed to investigate peculiar consequences of the well-known double-slit experiment in quantum mechanics, as well as the consequences of quantum entanglement.
The delayed-choice quantum eraser experiment investigates a paradox. If a photon manifests itself as though it had come by a single path to the detector, then "common sense" (which Wheeler and others challenge) says that it must have entered the double-slit device as a particle. If a photon manifests itself as though it had come by two indistinguishable paths, then it must have entered the double-slit device as a wave. Accordingly, if the experimental apparatus is changed while the photon is in mid‑flight, the photon may have to revise its prior "commitment" as to whether to be a wave or a particle. Wheeler pointed out that when these assumptions are applied to a device of interstellar dimensions, a last-minute decision made on Earth on how to observe a photon could alter a situation established millions or even billions of years earlier.
While delayed-choice experiments might seem to allow measurements made in the present to alter events that occurred in the past, this conclusion requires assuming a non-standard view of quantum mechanics. If a photon in flight is instead interpreted as being in a so-called "superposition of states"—that is, if it is allowed the potentiality of manifesting as a particle or wave, but during its time in flight is neither—then there is no causation paradox. This notion of superposition reflects the standard interpretation of quantum mechanics.
Introduction
In the basic double-slit experiment, a beam of light (usually from a laser) is directed perpendicularly towards a wall pierced by two parallel slit apertures. If a detection screen (anything from a sheet of white paper to a CCD) is put on the other side of the double-slit wall (far enough for light from both slits to overlap), a pattern of light and dark fringes will be observed, a pattern that is called an interference pattern. Other atomic-scale entities such as electrons are found to exhibit the same behavior when fired toward a double slit. By decreasing the brightness of the source sufficiently, individual particles that form the interference pattern are detectable. The emergence of an interference pattern suggests that each particle passing through the slits interferes with itself, and that therefore in some sense the particles are going through both slits at once. This is an idea that contradicts our everyday experience of discrete objects.
A well-known thought experiment, which played a vital role in the history of quantum mechanics (for example, see the discussion on Einstein's version of this experiment), demonstrated that if particle detectors are positioned at the slits, showing through which slit a photon goes, the interference pattern will disappear. This which-way experiment illustrates the complementarity principle that photons can behave as either particles or as waves, but cannot be simultaneously observed to be both a particle and a wave. However, technically feasible realizations of this experiment were not proposed until the 1970s.
Which-path information and the visibility of interference fringes are complementary quantities, meaning that information about a photon's path can be observed, or interference fringes can be observed, but they cannot both be observed in the same trial. In the double-slit experiment, conventional wisdom held that observing the particles' path inevitably disturbed them enough to destroy the interference pattern as a result of the Heisenberg uncertainty principle.
In 1982, Scully and Drühl pointed out a workaround alternative to this interpretation. They proposed to save the information about which slit the photon went through - or, in their setup, from which atom the photon was re-emitted - in the excited state of that atom. At this point the which-path information is known and no interference is observed. However, one can "erase" this information by making the atom to emit another photon and fall to the ground state. That on its own will not bring the interference pattern back, the which-path information can still be extracted from an appropriate measurement of the second photon. However, if the second photon is measured at a place where it could get to equally likely from any of the atoms, that successfully "erases" the which-path information. The original photon would now show the interference pattern (the position of its fringes depends on where exactly the second photon was observed, so that in the total statistics they average out and no fringes are seen). Since 1982, multiple experiments have demonstrated the validity of this so-called quantum "eraser".
A simple quantum-eraser experiment
A simple version of the quantum eraser can be described as follows: Rather than splitting one photon or its probability wave between two slits, the photon is subjected to a beam splitter. If one thinks in terms of a stream of photons being randomly directed by such a beam splitter to go down two paths that are kept from interaction, it would seem that no photon can then interfere with any other or with itself.
If the rate of photon production is reduced so that only one photon enters the apparatus at any one time, it becomes impossible to understand the photon as only moving through one path, because when the path outputs are redirected so that they coincide on a common detector or detectors, interference phenomena appear. This is similar to envisioning one photon in a two-slit apparatus: even though it is one photon, it still somehow interacts with both slits.

In the two diagrams in Fig. 1, photons are emitted one at a time from a laser symbolized by a yellow star. They pass through a 50% beam splitter (green block) that reflects or transmits 1/2 of the photons. The reflected or transmitted photons travel along two possible paths depicted by the red or blue lines.
In the top diagram, it seems as though the trajectories of the photons are known: If a photon emerges from the top of the apparatus, it seems as though it had to have come by way of the blue path, and if it emerges from the side of the apparatus, it seems as though it had to have come by way of the red path. However, it is important to keep in mind that the photon is in a superposition of the paths until it is detected. The assumption above—that it 'had to have come by way of' either path—is a form of the 'separation fallacy'.
In the bottom diagram, a second beam splitter is introduced at the top right. It recombines the beams corresponding to the red and blue paths. By introducing the second beam splitter, the usual way of thinking is that the path information has been "erased." However, we have to be careful, because the photon cannot be assumed to have 'really' gone along one or the other path. Recombining the beams results in interference phenomena at detection screens positioned just beyond each exit port. What issues to the right side displays reinforcement, and what issues toward the top displays cancellation. It is important to keep in mind however that the illustrated interferometer effects apply only to a single photon in a pure state. When dealing with a pair of entangled photons, the photon encountering the interferometer will be in a mixed state, and there will be no visible interference pattern without coincidence counting to select appropriate subsets of the data.
Delayed choice
Elementary precursors to current quantum-eraser experiments such as the "simple quantum eraser" described above have straightforward classical-wave explanations. Indeed, it could be argued that there is nothing particularly quantum about this experiment. Nevertheless, Jordan has argued on the basis of the correspondence principle, that despite the existence of classical explanations, first-order interference experiments such as the above can be interpreted as true quantum erasers.
These precursors use single-photon interference. Versions of the quantum eraser using entangled photons, however, are intrinsically non-classical. Because of that, in order to avoid any possible ambiguity concerning the quantum versus classical interpretation, most experimenters have opted to use nonclassical entangled-photon light sources to demonstrate quantum erasers with no classical analog.
Furthermore, the use of entangled photons enables the design and implementation of versions of the quantum eraser that are impossible to achieve with single-photon interference, such as the delayed-choice quantum eraser, which is the topic of this article.
The experiment of Kim et al. (1999)
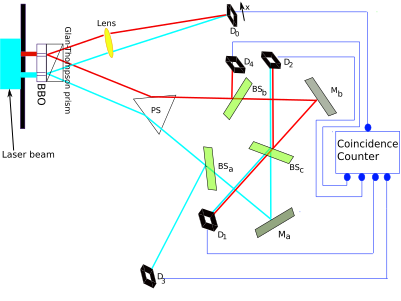
The experimental setup, described in detail in Kim et al., is illustrated in Fig 2. An argon laser generates individual 351.1 nm photons that pass through a double-slit apparatus (vertical black line in the upper left corner of the diagram).
An individual photon goes through one (or both) of the two slits. In the illustration, the photon paths are color-coded as red or light blue lines to indicate which slit the photon came through (red indicates slit A, light blue indicates slit B).
So far, the experiment is like a conventional two-slit experiment. However, after the slits, spontaneous parametric down-conversion (SPDC) is used to prepare an entangled two-photon state. This is done by a nonlinear optical crystal BBO (beta barium borate) that converts the photon (from either slit) into two identical, orthogonally polarized entangled photons with 1/2 the frequency of the original photon. The paths followed by these orthogonally polarized photons are caused to diverge by the Glan–Thompson prism.
One of these 702.2 nm photons, referred to as the "signal" photon (look at the red and light-blue lines going upwards from the Glan–Thompson prism) continues to the target detector called D0. During an experiment, detector D0 is scanned along its x axis, its motions controlled by a step motor. A plot of "signal" photon counts detected by D0 versus x can be examined to discover whether the cumulative signal forms an interference pattern.
The other entangled photon, referred to as the "idler" photon (look at the red and light-blue lines going downwards from the Glan–Thompson prism), is deflected by prism PS that sends it along divergent paths depending on whether it came from slit A or slit B.
Somewhat beyond the path split, the idler photons encounter beam splitters BSa, BSb, and BSc that each have a 50% chance of allowing the idler photon to pass through and a 50% chance of causing it to be reflected. Ma and Mb are mirrors.


The beam splitters and mirrors direct the idler photons towards detectors labeled D1, D2, D3 and D4. Note that:
- If an idler photon is recorded at detector D3, it can only have come from slit B.
- If an idler photon is recorded at detector D4, it can only have come from slit A.
- If an idler photon is detected at detector D1 or D2, it might have come from slit A or slit B.
- The optical path length measured from slit to D1, D2, D3, and D4 is 2.5 m longer than the optical path length from slit to D0. This means that any information that one can learn from an idler photon must be approximately 8 ns later than what one can learn from its entangled signal photon.
Detection of the idler photon by D3 or D4 provides delayed "which-path information" indicating whether the signal photon with which it is entangled had gone through slit A or B. On the other hand, detection of the idler photon by D1 or D2 provides a delayed indication that such information is not available for its entangled signal photon. Insofar as which-path information had earlier potentially been available from the idler photon, it is said that the information has been subjected to a "delayed erasure".
By using a coincidence counter, the experimenters were able to isolate the entangled signal from photo-noise, recording only events where both signal and idler photons were detected (after compensating for the 8 ns delay). Refer to Figs 3 and 4.
- When the experimenters looked at the signal photons whose entangled idlers were detected at D1 or D2, they detected interference patterns.
- However, when they looked at the signal photons whose entangled idlers were detected at D3 or D4, they detected simple diffraction patterns with no interference.
Significance
This result is similar to that of the double-slit experiment since interference is observed when it is extracted according to phase value (R01 or R02). Note that the phase cannot be measured if the photon's path (the slit through which it passes) is known.

However, what makes this experiment possibly astonishing is that, unlike in the classic double-slit experiment, the choice of whether to preserve or erase the which-path information of the idler was not made until 8 ns after the position of the signal photon had already been measured by D0.
Detection of signal photons at D0 does not directly yield any which-path information. Detection of idler photons at D3 or D4, which provide which-path information, means that no interference pattern can be observed in the jointly detected subset of signal photons at D0. Likewise, detection of idler photons at D1 or D2, which do not provide which-path information, means that interference patterns can be observed in the jointly detected subset of signal photons at D0.
In other words, even though an idler photon is not observed until long after its entangled signal photon arrives at D0 due to the shorter optical path for the latter, interference at D0 is determined by whether a signal photon's entangled idler photon is detected at a detector that preserves its which-path information (D3 or D4), or at a detector that erases its which-path information (D1 or D2).
Some have interpreted this result to mean that the delayed choice to observe or not observe the path of the idler photon changes the outcome of an event in the past. Note in particular that an interference pattern may only be pulled out for observation after the idlers have been detected (i.e., at D1 or D2).
The total pattern of all signal photons at D0, whose entangled idlers went to multiple different detectors, will never show interference regardless of what happens to the idler photons. One can get an idea of how this works by looking at the graphs of R01, R02, R03, and R04, and observing that the peaks of R01 line up with the troughs of R02 (i.e. a π phase shift exists between the two interference fringes). R03 shows a single maximum, and R04, which is experimentally identical to R03 will show equivalent results. The entangled photons, as filtered with the help of the coincidence counter, are simulated in Fig. 5 to give a visual impression of the evidence available from the experiment. In D0, the sum of all the correlated counts will not show interference. If all the photons that arrive at D0 were to be plotted on one graph, one would see only a bright central band.
Implications
Retrocausality
Delayed-choice experiments raise questions about the causal connections between the events. If events at D1, D2, D3, D4 determine outcomes at D0, then the effects might seem to precede their causes in time.
Consensus: no retrocausality
However, the interference pattern can only be seen retroactively once the idler photons have been detected and the detection information used to select subsets of signal photons.
Moreover, it's observed that the apparent retroactive action vanishes if the effects of observations on the state of the entangled signal and idler photons are considered in their historic order. Specifically, in the case when detection/deletion of which-way information happens before the detection on D0, the standard simplistic explanation says "The detector Di, at which the idler photon is detected, determines the probability distribution at D0 for the signal photon". Similarly, in the case when D0 precedes detection of the idler photon, the following description is just as accurate: "The position at D0 of the detected signal photon determines the probabilities for the idler photon to hit either of D1, D2, D3 or D4". These are just equivalent ways of formulating the correlations of entangled photons' observables in an intuitive causal way, so one may choose any of those (in particular, that one where the cause precedes the consequence and no retrograde action appears in the explanation).
The total pattern of signal photons at the primary detector never shows interference (see Fig. 5), so it is not possible to deduce what will happen to the idler photons by observing the signal photons alone. In a paper by Johannes Fankhauser, it is shown that the delayed choice quantum eraser experiment resembles a Bell-type scenario in which the paradox's resolution is rather trivial, and so there really is no mystery. Moreover, it gives a detailed account of the experiment in the de Broglie-Bohm picture with definite trajectories arriving at the conclusion that there is no "backwards in time influence" present. The delayed-choice quantum eraser does not communicate information in a retro-causal manner because it takes another signal, one which must arrive by a process that can go no faster than the speed of light, to sort the superimposed data in the signal photons into four streams that reflect the states of the idler photons at their four distinct detection screens.
A theorem proven by Phillippe Eberhard shows that if the accepted equations of relativistic quantum field theory are correct, faster than light communications is impossible. (See reference for a treatment emphasizing the role of conditional probabilities.)
Other delayed-choice quantum-eraser experiments
| This section needs expansion. You can help by adding to it. (February 2014) |
Many refinements and extensions of Kim et al. delayed-choice quantum eraser have been performed or proposed. Only a small sampling of reports and proposals are given here:
Scarcelli et al. (2007) reported on a delayed-choice quantum-eraser experiment based on a two-photon imaging scheme. After detecting a photon passed through a double-slit, a random delayed choice was made to erase or not erase the which-path information by the measurement of its distant entangled twin; the particle-like and wave-like behavior of the photon were then recorded simultaneously and respectively by only one set of joint detectors.
Peruzzo et al. (2012) have reported on a quantum delayed-choice experiment based on a quantum-controlled beam splitter, in which particle and wave behaviors were investigated simultaneously. The quantum nature of the photon's behavior was tested with a Bell inequality, which replaced the delayed choice of the observer.
Rezai et al. (2018) have combined the Hong-Ou-Mandel interference with a delayed choice quantum eraser. They impose two incompatible photons onto a beam-splitter, such that no interference pattern could be observed. When the output ports are monitored in an integrated fashion (i.e. counting all the clicks), no interference occurs. Only when the outcoming photons are polarization analysed and the right subset is selected, quantum interference in the form of a Hong-Ou-Mandel dip occurs.
The construction of solid-state electronic Mach–Zehnder interferometers (MZI) has led to proposals to use them in electronic versions of quantum-eraser experiments. This would be achieved by Coulomb coupling to a second electronic MZI acting as a detector.
Entangled pairs of neutral kaons have also been examined and found suitable for investigations using quantum marking and quantum-erasure techniques.
A quantum eraser has been proposed using a modified Stern-Gerlach setup. In this proposal, no coincident counting is required, and quantum erasure is accomplished by applying an additional Stern-Gerlach magnetic field.
Notes
- Stanford Encyclopedia of Philosophy, "More recently, the Bell-type experiments have been interpreted by some as if quantum events could be connected in such a way that the past light cone might be accessible under non-local interaction; not only in the sense of action at a distance but as backward causation. One of the most enticing experiments of this kind is the Delayed Choice Quantum Eraser designed by Yoon-Ho Kim et al. (2000). It is a rather complicated construction. It is set up to measure correlated pairs of photons, which are in an entangled state so that one of the two photons is detected 8 nanoseconds before its partner. The results of the experiment are quite amazing. They seem to indicate that the behavior of the photons detected these 8 nanoseconds before their partners is determined by how the partners will be detected. Indeed it might be tempting to interpret these results as an example of the future causing the past. The result is, however, in accordance with the predictions of quantum mechanics." http://plato.stanford.edu/entries/causation-backwards/.
- "... the future measurements do not in any way change the data you collected today. But the future measurements do influence the kinds of details you can invoke when you subsequently describe what happened today. Before you have the results of the idler photon measurements, you really can't say anything at all about the which-path history of any given signal photon. However, once you have the results, you conclude that signal photons whose idler partners were successfully used to ascertain which-path information can be described as having ... traveled either left or right. You also conclude that signal photons whose idler partners had their which-path information erased cannot be described as having ... definitely gone one way or the other (a conclusion you can convincingly confirm by using the newly acquired idler photon data to expose the previously hidden interference pattern among this latter class of signal photons). We thus see that the future helps shape the story you tell of the past." — Brian Greene, The Fabric of the Cosmos, pp 198–199
- The Kim paper says: P. 1f: The experiment is designed in such a way that L0, the optical distance between atoms A, B and detector D0, is much shorter than Li, which is the optical distance between atoms A, B and detectors D1, D2, D3, and D4, respectively. So that D0 will be triggered much earlier by photon 1. After the registration of photon 1, we look at these "delayed" detection events of D1, D2, D3, and D4 which have constant time delays, i ≃ (Li − L0)/c, relative to the triggering time of D0. P.2: In this experiment the optical delay (Li − L0) is chosen to be ≃ 2.5m, where L0 is the optical distance between the output surface of BBO and detector D0, and Li is the optical distance between the output surface of the BBO and detectors D1, D2, D3, and D4, respectively. This means that any information one can learn from photon 2 must be at least 8ns later than what one has learned from the registration of photon 1. Compared to the 1ns response time of the detectors, 2.5m delay is good enough for a "delayed erasure". P. 3: The which-path or both-path information of a quantum can be erased or marked by its entangled twin even after the registration of the quantum. P. 2: After the registration of photon 1, we look at these "delayed" detection events of D1, D2, D3, and D4 which have constant time delays, i ≃ (Li − L0)/c, relative to the triggering time of D0. It is easy to see these "joint detection" events must have resulted from the same photon pair. (Emphasis added. This is the point at which what is going on at D0 can be figured out.)
References
- ^ Kim, Yoon-Ho; R. Yu; S. P. Kulik; Y. H. Shih; Marlan Scully (2000). "A Delayed "Choice" Quantum Eraser". Physical Review Letters. 84 (1): 1–5. arXiv:quant-ph/9903047. Bibcode:2000PhRvL..84....1K. doi:10.1103/PhysRevLett.84.1. PMID 11015820. S2CID 5099293.
- Ma, Xiao-Song; Kofler, Johannes; Qarry, Angie; Tetik, Nuray; Scheidl, Thomas; Ursin, Rupert; Ramelow, Sven; Herbst, Thomas; Ratschbacher, Lothar; Fedrizzi, Alessandro; Jennewein, Thomas; Zeilinger, Anton (2013). "Quantum erasure with causally disconnected choice". Proceedings of the National Academy of Sciences. 110 (4): 1221–1226. arXiv:1206.6578. Bibcode:2013PNAS..110.1221M. doi:10.1073/pnas.1213201110. PMC 3557028. PMID 23288900.
Our results demonstrate that the viewpoint that the system photon behaves either definitely as a wave or definitely as a particle would require faster-than-light communication. Because this would be in strong tension with the special theory of relativity, we believe that such a viewpoint should be given up entirely.
- Peruzzo, A.; Shadbolt, P.; Brunner, N.; Popescu, S.; O'Brien, J. L. (2012). "A Quantum Delayed-Choice Experiment". Science. 338 (6107): 634–637. arXiv:1205.4926. Bibcode:2012Sci...338..634P. doi:10.1126/science.1226719. PMID 23118183. S2CID 3725159. This experiment uses Bell inequalities to replace the delayed choice devices, but it achieves the same experimental purpose in an elegant and convincing way.
- ^ Feynman, Richard P.; Robert B. Leighton; Matthew Sands (1965). The Feynman Lectures on Physics, Vol. 3. US: Addison-Wesley. pp. 1.1–1.8. ISBN 978-0-201-02118-9.
- Donati, O; Missiroli, G F; Pozzi, G (1973). "An Experiment on Electron Interference". American Journal of Physics. 41 (5): 639–644. Bibcode:1973AmJPh..41..639D. doi:10.1119/1.1987321.
- Greene, Brian (2003). The Elegant Universe. Random House, Inc. ISBN 978-0-375-70811-4.
- Harrison, David (2002). "Complementarity and the Copenhagen Interpretation of Quantum Mechanics". UPSCALE. Dept. of Physics, U. of Toronto. Retrieved 2008-06-21.
- Cassidy, David (2008). "Quantum Mechanics 1925–1927: Triumph of the Copenhagen Interpretation". Werner Heisenberg. American Institute of Physics. Archived from the original on 2016-01-14. Retrieved 2008-06-21.
- Boscá Díaz-Pintado, María C. (29–31 March 2007). "Updating the wave-particle duality". 15th UK and European Meeting on the Foundations of Physics. Leeds, UK. Retrieved 2008-06-21.
- Bartell, L. (1980). "Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behavior". Physical Review D. 21 (6): 1698–1699. Bibcode:1980PhRvD..21.1698B. doi:10.1103/PhysRevD.21.1698.
- Scully, Marlan O.; Kai Drühl (1982). "Quantum eraser: A proposed photon correlation experiment concerning observation and "delayed choice" in quantum mechanics". Physical Review A. 25 (4): 2208–2213. Bibcode:1982PhRvA..25.2208S. doi:10.1103/PhysRevA.25.2208.
- Zajonc, A. G.; Wang, L. J.; Zou, X. Y.; Mandel, L. (1991). "Quantum eraser". Nature. 353 (6344): 507–508. Bibcode:1991Natur.353..507Z. doi:10.1038/353507b0. S2CID 4265543.
- Herzog, T. J.; Kwiat, P. G.; Weinfurter, H.; Zeilinger, A. (1995). "Complementarity and the quantum eraser" (PDF). Physical Review Letters. 75 (17): 3034–3037. Bibcode:1995PhRvL..75.3034H. doi:10.1103/PhysRevLett.75.3034. PMID 10059478. Archived from the original (PDF) on 24 December 2013. Retrieved 13 February 2014.
- Walborn, S. P.; et al. (2002). "Double-Slit Quantum Eraser". Phys. Rev. A. 65 (3): 033818. arXiv:quant-ph/0106078. Bibcode:2002PhRvA..65c3818W. doi:10.1103/PhysRevA.65.033818. S2CID 55122015.
- Jacques, Vincent; Wu, E; Grosshans, Frédéric; Treussart, François; Grangier, Philippe; Aspect, Alain; Rochl, Jean-François (2007). "Experimental Realization of Wheeler's Delayed-Choice Gedanken Experiment". Science. 315 (5814): 966–968. arXiv:quant-ph/0610241. Bibcode:2007Sci...315..966J. doi:10.1126/science.1136303. PMID 17303748. S2CID 6086068.
- Chiao, R. Y.; P. G. Kwiat; Steinberg, A. M. (1995). "Quantum non-locality in two-photon experiments at Berkeley". Quantum and Semiclassical Optics: Journal of the European Optical Society Part B. 7 (3): 259–278. arXiv:quant-ph/9501016. Bibcode:1995QuSOp...7..259C. doi:10.1088/1355-5111/7/3/006. S2CID 118987962.
- Jordan, T. F. (1993). "Disappearance and reappearance of macroscopic quantum interference". Physical Review A. 48 (3): 2449–2450. Bibcode:1993PhRvA..48.2449J. doi:10.1103/PhysRevA.48.2449. PMID 9909872.
- Ionicioiu, R.; Terno, D. R. (2011). "Proposal for a quantum delayed-choice experiment". Phys. Rev. Lett. 107 (23): 230406. arXiv:1103.0117. Bibcode:2011PhRvL.107w0406I. doi:10.1103/physrevlett.107.230406. PMID 22182073. S2CID 44297197.
- J.A. Wheeler, Quantum Theory and Measurement, Princeton University Press p.192-213
- Greene, Brian (2004). The Fabric of the Cosmos: Space, Time, and the Texture of Reality. Alfred A. Knopf. p. 198. ISBN 978-0-375-41288-2.
- Greene, Brian (2004). The Fabric of the Cosmos. Alfred A. Knopf. ISBN 978-0-375-41288-2.
- Fankhauser, Johannes (2019). "Taming the Delayed Choice Quantum Eraser". Quanta. 8: 44–56. arXiv:1707.07884. doi:10.12743/quanta.v8i1.88. S2CID 53574007.
- Eberhard, Phillippe H.; Ronald R. Ross (1989). "Quantum field theory cannot provide faster-than-light communication" (PDF). Foundations of Physics Letters. 2 (2): 127–149. Bibcode:1989FoPhL...2..127E. doi:10.1007/BF00696109. S2CID 123217211.
- Gaasbeek, Bram (2010). "Demystifying the Delayed Choice Experiments". arXiv:1007.3977 .
- Scarcelli, G.; Zhou, Y.; Shih, Y. (2007). "Random delayed-choice quantum eraser via two-photon imaging". The European Physical Journal D. 44 (1): 167–173. arXiv:quant-ph/0512207. Bibcode:2007EPJD...44..167S. doi:10.1140/epjd/e2007-00164-y. S2CID 10267634.
- Peruzzo, A.; Shadbolt, P.; Brunner, N.; Popescu, S.; O'Brien, J. L. (2012). "A quantum delayed-choice experiment". Science. 338 (6107): 634–637. arXiv:1205.4926. Bibcode:2012Sci...338..634P. doi:10.1126/science.1226719. PMID 23118183. S2CID 3725159.
- Rezai, M.; Wrachtrup, J.; Gerhardt, I. (2018). "Coherence Properties of Molecular Single Photons for Quantum Networks". Physical Review X. 8 (3): 031026. Bibcode:2018PhRvX...8c1026R. doi:10.1103/PhysRevX.8.031026.
- Dressel, J.; Choi, Y.; Jordan, A. N. (2012). "Measuring which-path information with coupled electronic Mach-Zehnder interferometers". Physical Review B. 85 (4): 045320. arXiv:1105.2587. doi:10.1103/physrevb.85.045320. S2CID 110142737.
- Bramon, A.; Garbarino, G.; Hiesmayr, B. C. (2004). "Quantum marking and quantum erasure for neutral kaons". Physical Review Letters. 92 (2): 020405. arXiv:quant-ph/0306114. Bibcode:2004PhRvL..92b0405B. doi:10.1103/physrevlett.92.020405. PMID 14753924. S2CID 36478919.
- Qureshi, T.; Rahman, Z. (2012). "Quantum eraser using a modified Stern-Gerlach setup". Progress of Theoretical Physics. 127 (1): 71–78. arXiv:quant-ph/0501010. Bibcode:2012PThPh.127...71Q. doi:10.1143/PTP.127.71. S2CID 59470770.
External links
- Presentation of the experiment
- The Notorious Delayed-Choice Quantum Eraser
- Delayed-choice quantum eraser
- Trifonov, A.; Björk, G.; Söderholm, J.; Tsegaye, T. (2002). "Comprehensive experimental test of quantum erasure". The European Physical Journal D. 18 (2): 251–258. arXiv:quant-ph/0009097. Bibcode:2002EPJD...18..251T. doi:10.1140/epjd/e20020030. S2CID 119026478.
- Ma, Xiao-Song; Kofler, Johannes; Qarry, Angie; Tetik, Nuray; Scheidl, Thomas; Ursin, Rupert; Ramelow, Sven; Herbst, Thomas; Ratschbacher, Lothar; Fedrizzi, Alessandro; Jennewein, Thomas; Zeilinger, Anton (2013). "Quantum erasure with causally disconnected choice". Proceedings of the National Academy of Sciences. 110 (4): 1221–1226. arXiv:1206.6578. Bibcode:2013PNAS..110.1221M. doi:10.1073/pnas.1213201110. PMC 3557028. PMID 23288900.
- Delayed Choice Quantum Eraser Experiment Explained, YouTube (with an explanation of the experiment by Kim et al. in minutes 3:31 to 9:09)
- Fankhauser, Johannes (2019). "Taming the Delayed Choice Quantum Eraser". Quanta. 8: 44–56. arXiv:1707.07884. doi:10.12743/quanta.v8i1.88. S2CID 53574007.
