| Revision as of 04:49, 26 February 2014 editMark viking (talk | contribs)Extended confirmed users19,285 edits →top: Added wl, spelling← Previous edit | Latest revision as of 17:45, 24 October 2024 edit undoJustinkunimune (talk | contribs)Extended confirmed users1,922 edits →Methods for one-dimensional integrals: brining up round-off error here is misleading, since integration error usually dominates. better to just leave it at "error"; it gets the point across more clearly anyway. | ||
| (181 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Methods of calculating definite integrals}} | |||
| ] | |||
| ] | |||
| In ], '''numerical integration''' constitutes a broad family of ]s for calculating the numerical value of a definite ], and by extension, the term is also sometimes used to describe the ]. This article focuses on calculation of definite integrals. The term '''numerical quadrature''' (often abbreviated to ]) is more or less a synonym for ''numerical integration'', especially as applied to one-dimensional integrals. Numerical integration over more than one dimension is sometimes described as '''cubature''',<ref>{{MathWorld | urlname=Cubature | title=Cubature }}</ref> although the meaning of ''quadrature'' is understood for higher dimensional integration as well. | |||
| {{Differential equations}} | |||
| In ], '''numerical integration''' comprises a broad family of ]s for calculating the numerical value of a definite ]. | |||
| The term '''numerical quadrature''' (often abbreviated to '''quadrature''') is more or less a synonym for "numerical integration", especially as applied to one-dimensional integrals. Some authors refer to numerical integration over more than one dimension as '''cubature''';<ref>{{MathWorld | urlname=Cubature | title=Cubature }}</ref> others take "quadrature" to include higher-dimensional integration. | |||
| The basic problem in numerical integration is to compute an approximate solution to a definite integral | The basic problem in numerical integration is to compute an approximate solution to a definite integral | ||
| :<math>\int_a^b |
:<math>\int_a^b f(x) \, dx</math> | ||
| to a given degree of accuracy. If {{math|''f''(''x'')}} is a smooth function integrated over a small number of dimensions, and the domain of integration is bounded, there are many methods for approximating the integral to the desired precision. | |||
| Numerical integration has roots in the geometrical problem of finding a square with the same area as a given plane figure ('']'' or ''squaring''), as in the ]. | |||
| The term is also sometimes used to describe the ]. | |||
| == Motivation and need == | |||
| There are several reasons for carrying out numerical integration, as opposed to analytical integration by finding the ]: | |||
| # The integrand {{math|''f'' (''x'')}} may be known only at certain points, such as obtained by ]. Some ] and other computer applications may need numerical integration for this reason. | |||
| to a given degree of accuracy. If {{math|''f(x)''}} is a smooth function integrated over a small number of dimensions, and the domain of integration is bounded, there are many methods for approximating the integral to the desired precision. | |||
| # A formula for the integrand may be known, but it may be difficult or impossible to find an antiderivative that is an ]. An example of such an integrand is {{math|1=''f'' (''x'') = exp(−''x''{{sup|2}})}}, the antiderivative of which (the ], times a constant) cannot be written in ]. {{See also|nonelementary integral|}} | |||
| # It may be possible to find an antiderivative symbolically, but it may be easier to compute a numerical approximation than to compute the antiderivative. That may be the case if the antiderivative is given as an infinite series or product, or if its evaluation requires a ] that is not available. | |||
| == History == | == History == | ||
| {{main|Quadrature (mathematics)}} | {{main|Quadrature (mathematics)}} | ||
| The term "numerical integration" first appears in 1915 in the publication ''A Course in Interpolation and Numeric Integration for the Mathematical Laboratory'' by ].<ref>{{cite web|url=http://jeff560.tripod.com/q.html|title=Earliest Known Uses of Some of the Words of Mathematics (Q)|website=jeff560.tripod.com|access-date=31 March 2018}}</ref> | |||
| '''Quadrature''' is a historical mathematical term that means calculating area. Quadrature problems have served as one of the main sources of ]. ], according to the ] doctrine, understood calculation of ] as the process of constructing geometrically a ] having the same area (''squaring''). That is why the process was named '''quadrature'''. For example, a ], ], ]. This construction must be performed only by means of ]. | |||
| "Quadrature" is a historical mathematical term that means calculating area. Quadrature problems have served as one of the main sources of ]. ], according to the ] doctrine, understood calculation of ] as the process of constructing geometrically a ] having the same area (''squaring''). That is why the process was named "quadrature". For example, a ], ], ]. This construction must be performed only by means of ]. | |||
| ]]] | |||
| The ancient Babylonians used the ] to integrate the motion of ] along the ].<ref>{{cite journal|author1=Mathieu Ossendrijver|title=Ancient Babylonian astronomers calculated Jupiter's position from the area under a time-velocity graph|journal=Science|date=Jan 29, 2016|doi=10.1126/science.aad8085|volume=351|issue=6272|pages=482–484|pmid=26823423|bibcode=2016Sci...351..482O|s2cid=206644971 }}</ref> | |||
| ] ]] | |||
| For a quadrature of a rectangle with the sides ''a'' and ''b'' it is necessary to construct a square with the side <math>x =\sqrt {ab}</math> (the ] of ''a'' and ''b''). For this purpose it is possible to use the following fact: if we draw the circle with the sum of ''a'' and ''b'' as the diameter, then the height BH (from a point of their connection to crossing with a circle) equals their geometric mean. The similar geometrical construction solves a problem of a quadrature for a parallelogram and a triangle. | For a quadrature of a rectangle with the sides ''a'' and ''b'' it is necessary to construct a square with the side <math>x =\sqrt {ab}</math> (the ] of ''a'' and ''b''). For this purpose it is possible to use the following fact: if we draw the circle with the sum of ''a'' and ''b'' as the diameter, then the height BH (from a point of their connection to crossing with a circle) equals their geometric mean. The similar geometrical construction solves a problem of a quadrature for a parallelogram and a triangle. | ||
| ] | ] | ||
| Problems of quadrature for curvilinear figures are much more difficult. The ] with compass and straightedge had been proved in the 19th century to be impossible. Nevertheless, for some figures (for example ]) a quadrature can be performed. The quadratures of a sphere surface and a ] done by ] became the highest achievement of the antique analysis. | Problems of quadrature for curvilinear figures are much more difficult. The ] with compass and straightedge had been proved in the 19th century to be impossible. Nevertheless, for some figures (for example the ]) a quadrature can be performed. The quadratures of a sphere surface and a ] done by ] became the highest achievement of the antique analysis. | ||
| * The area of the surface of a sphere is equal to quadruple the area of a ] of this sphere. | * The area of the surface of a sphere is equal to quadruple the area of a ] of this sphere. | ||
| * The area of a segment of the ] cut from it by a straight line is 4/3 the area of the triangle inscribed in this segment. | * The area of a segment of the ] cut from it by a straight line is 4/3 the area of the triangle inscribed in this segment. | ||
| For the proof of the results Archimedes used the ] of ]. | For the proof of the results Archimedes used the ] of ]. | ||
| In medieval Europe the quadrature meant calculation of area by any method. More often the ] was used; it was less rigorous, but more simple and powerful. With its help ] and ] found the area of a ] arch, ] investigated the area under a ] (''Opus Geometricum'', 1647), and ], de Saint-Vincent's pupil and commentator noted the relation of this area to ]s. | In medieval Europe the quadrature meant calculation of area by any method. More often the ] was used; it was less rigorous, but more simple and powerful. With its help ] and ] found the area of a ] arch, ] investigated the area under a ] (''Opus Geometricum'', 1647), and ], de Saint-Vincent's pupil and commentator, noted the relation of this area to ]s. | ||
| ] algebrised this method: he wrote in his ''Arithmetica Infinitorum'' (1656) series that we now call the ], and he calculated their values. ] and ] made further progress: quadratures for some ] and ]s. ] successfully performed a quadrature of some ]. | ] algebrised this method: he wrote in his ''Arithmetica Infinitorum'' (1656) series that we now call the ], and he calculated their values. ] and ] made further progress: quadratures for some ] and ]s. ] successfully performed a quadrature of some ]. | ||
| The quadrature of the hyperbola by Saint-Vincent and de Sarasa provided a new ], the ], of critical importance. | The quadrature of the hyperbola by Saint-Vincent and de Sarasa provided a new ], the ], of critical importance. | ||
| With the invention of ] came a universal method for area calculation. In response, the term |
With the invention of ] came a universal method for area calculation. In response, the term "quadrature" has become traditional, and instead the modern phrase "''computation of a univariate definite integral''" is more common. | ||
| == |
==Methods for one-dimensional integrals== | ||
| A '''quadrature rule''' is an approximation of the ] of a ], usually stated as a ] of function values at specified points within the domain of integration. | |||
| Numerical integration methods can generally be described as combining evaluations of the integrand to get an approximation to the integral. The integrand is evaluated at a finite set of points called '''''integration points''''' and a weighted sum of these values is used to approximate the integral. The integration points and weights depend on the specific method used and the accuracy required from the approximation. | |||
| There are several reasons for carrying out numerical integration. | |||
| The integrand ''f(x)'' may be known only at certain points, | |||
| such as obtained by ]. | |||
| Some ] and other computer applications may need numerical integration for this reason. | |||
| A formula for the integrand may be known, but it may be difficult or impossible to find an ] that is an ]. An example of such an integrand is ''f(x)'' = exp(−''x''<sup>''2''</sup>), the antiderivative of which (the ], times a constant) cannot be written in ]. | |||
| It may be possible to find an antiderivative symbolically, but it may be easier to compute a numerical approximation than to compute the antiderivative. That may be the case if the antiderivative is given as an infinite series or product, or if its evaluation requires a ] that is not available. | |||
| ==Methods for one-dimensional integrals== | |||
| An important part of the analysis of any numerical integration method is to study the behavior of the approximation error as a function of the number of integrand evaluations. A method that yields a small error for a small number of evaluations is usually considered superior. Reducing the number of evaluations of the integrand reduces the number of arithmetic operations involved, and therefore reduces the total error. Also, each evaluation takes time, and the integrand may be arbitrarily complicated. | |||
| Numerical integration methods can generally be described as combining evaluations of the integrand to get an approximation to the integral. The integrand is evaluated at a finite set of points called '''integration points''' and a weighted sum of these values is used to approximate the integral. The integration points and weights depend on the specific method used and the accuracy required from the approximation. | |||
| ===Quadrature rules based on step functions=== | |||
| An important part of the analysis of any numerical integration method is to study the behavior of the approximation error as a function of the number of integrand evaluations. | |||
| A "brute force" kind of numerical integration can be done, if the integrand is reasonably well-behaved (i.e. ] ] and of ]), by evaluating the integrand with very small increments. | |||
| A method that yields a small error for a small number of evaluations is usually considered superior. | |||
| Reducing the number of evaluations of the integrand reduces the number of arithmetic operations involved, | |||
| and therefore reduces the total ]. | |||
| Also, | |||
| each evaluation takes time, and the integrand may be arbitrarily complicated. | |||
| ] | |||
| A 'brute force' kind of numerical integration can be done, if the integrand is reasonably well-behaved (i.e. ] ] and of ]), by evaluating the integrand with very small increments. | |||
| This simplest method approximates the function by a ] (a piecewise constant function, or a segmented polynomial of degree zero) that passes through the point <math display="inline"> \left( \frac{a+b}{2}, f \left( \frac{a+b}{2} \right)\right) </math>. This is called the ''midpoint rule'' or '']'' | |||
| <math display="block">\int_a^b f(x)\, dx \approx (b-a) f\left(\frac{a+b}{2}\right).</math> | |||
| ===Quadrature rules based on interpolating functions=== | ===Quadrature rules based on interpolating functions=== | ||
| A large class of quadrature rules can be derived by constructing ] functions that are easy to integrate. Typically these interpolating functions are ]s. In practice, since polynomials of very high degree tend to ], only polynomials of low degree are used, typically linear and quadratic. | |||
| ] | |||
| A large class of quadrature rules can be derived by constructing ] functions that are easy to integrate. Typically these interpolating functions are ]s. | |||
| The interpolating function may be a straight line (an ], i.e. a polynomial of degree 1) | |||
| passing through the points <math> \left( a, f(a)\right) </math> and <math> \left( b, f(b)\right) </math>. | |||
| This is called the '']'' | |||
| <math display="block">\int_a^b f(x)\, dx \approx (b-a) \left(\frac{f(a) + f(b)}{2}\right).</math> | |||
| ] | ] | ||
| For either one of these rules, we can make a more accurate approximation by breaking up the interval <math> </math> into some number <math> n </math> of subintervals, computing an approximation for each subinterval, then adding up all the results. This is called a ''composite rule'', ''extended rule'', or ''iterated rule''. For example, the composite trapezoidal rule can be stated as | |||
| The simplest method of this type is to let the interpolating function be a constant function (a polynomial of degree zero) that passes through the point ((''a''+''b'')/2, ''f''((''a''+''b'')/2)). This is called the ''midpoint rule'' or '']''. | |||
| <math display="block">\int_a^b f(x)\, dx \approx | |||
| \frac{b-a}{n} \left( {f(a) \over 2} + \sum_{k=1}^{n-1} \left( f \left( a + k \frac{b-a}{n} \right) \right) + {f(b) \over 2} \right),</math> | |||
| where the subintervals have the form <math> \subset , </math> with <math display="inline">h = \frac{b - a}{n}</math> and <math>k = 0,\ldots,n-1. </math> Here we used subintervals of the same length <math> h </math> but one could also use intervals of varying length <math> \left( h_k \right)_k </math>. | |||
| :<math>\int_a^b f(x)\,dx \approx (b-a) \, f\left(\frac{a+b}{2}\right).</math> | |||
| Interpolation with polynomials evaluated at equally spaced points in <math> </math> yields the ], of which the rectangle rule and the trapezoidal rule are examples. ], which is based on a polynomial of order 2, is also a Newton–Cotes formula. | |||
| ] | |||
| The interpolating function may be an ] (a polynomial of degree 1) | |||
| that passes through the points (''a'', ''f''(''a'')) and (''b'', ''f''(''b'')). | |||
| This is called the '']''. | |||
| Quadrature rules with equally spaced points have the very convenient property of ''nesting''. The corresponding rule with each interval subdivided includes all the current points, so those integrand values can be re-used. | |||
| :<math>\int_a^b f(x)\,dx \approx (b-a) \, \frac{f(a) + f(b)}{2}.</math> | |||
| If we allow the intervals between interpolation points to vary, we find another group of quadrature formulas, such as the ] formulas. A Gaussian quadrature rule is typically more accurate than a Newton–Cotes rule that uses the same number of function evaluations, if the integrand is ] (i.e., if it is sufficiently differentiable). Other quadrature methods with varying intervals include ] (also called Fejér quadrature) methods, which do nest. | |||
| ] | |||
| For either one of these rules, we can make a more accurate approximation by breaking up the interval into some number ''n'' of subintervals, computing an approximation for each subinterval, then adding up all the results. This is called a ''composite rule'', ''extended rule'', or ''iterated rule''. For example, the composite trapezoidal rule can be stated as | |||
| :<math>\int_a^b f(x)\,dx \approx \frac{b-a}{n} \left( {f(a) \over 2} + \sum_{k=1}^{n-1} \left( f \left( a+k \frac{b-a}{n} \right) \right) + {f(b) \over 2} \right)</math> | |||
| where the subintervals have the form , with ''h'' = (''b''−''a'')/''n'' and ''k'' = 0, 1, 2, ..., ''n''−1. | |||
| Interpolation with polynomials evaluated at equally spaced points in yields the ], of which the rectangle rule and the trapezoidal rule are examples. ], which is based on a polynomial of order 2, is also a Newton–Cotes formula. | |||
| Quadrature rules with equally spaced points have the very convenient property of <em>nesting</em>. The corresponding rule with each interval subdivided includes all the current points, so those integrand values can be re-used. | |||
| If we allow the intervals between interpolation points to vary, we find another group of quadrature formulas, such as the ] formulas. A Gaussian quadrature rule is typically more accurate than a Newton–Cotes rule, which requires the same number of function evaluations, if the integrand is ] (i.e., if it is sufficiently differentiable). Other quadrature methods with varying intervals include ] (also called Fejér quadrature) methods, which do nest. | |||
| Gaussian quadrature rules do not nest, but the related ]s do. | Gaussian quadrature rules do not nest, but the related ]s do. | ||
| === Adaptive algorithms === | === Adaptive algorithms === | ||
| {{ |
{{excerpt|Adaptive quadrature}} | ||
| If ''f(x)'' does not have many derivatives at all points, or if the derivatives become large, then Gaussian quadrature is often insufficient. In this case, an algorithm similar to the following will perform better: | |||
| <source lang=python> | |||
| def calculate_definite_integral_of_f(f, initial_step_size): | |||
| ''' | |||
| This algorithm calculates the definite integral of a function | |||
| from 0 to 1, adaptively, by choosing smaller steps near | |||
| problematic points. | |||
| ''' | |||
| x = 0.0 | |||
| h = initial_step_size | |||
| accumulator = 0.0 | |||
| while x < 1.0: | |||
| if x + h > 1.0: | |||
| h = 1.0 - x | |||
| quad_this_step = | |||
| if error_too_big_in_quadrature_of_over_range(f, ): | |||
| h = make_h_smaller(h) | |||
| else: | |||
| accumulator += quadrature_of_f_over_range(f, ) | |||
| x += h | |||
| if error_too_small_in_quadrature_of_over_range(f, ): | |||
| h = make_h_larger(h) # Avoid wasting time on tiny steps. | |||
| return accumulator | |||
| </source> | |||
| Some details of the algorithm require careful thought. For many cases, estimating the error from quadrature over an interval for a function ''f''(''x'') isn't obvious. One popular solution is to use two different rules of quadrature, and use their difference as an estimate of the error from quadrature. The other problem is deciding what "too large" or "very small" signify. A <em>local</em> criterion for "too large" is that the quadrature error should not be larger than ''t'' · ''h'' where ''t'', a real number, is the tolerance we wish to set for global error. Then again, if ''h'' is already tiny, it may not be worthwhile to make it even smaller even if the quadrature error is apparently large. A <em>global</em> criterion is that the sum of errors on all the intervals should be less than ''t''. This type of error analysis is usually called "a posteriori" since we compute the error after having computed the approximation. | |||
| Heuristics for adaptive quadrature are discussed by Forsythe et al. (Section 5.4). | |||
| === Extrapolation methods === | === Extrapolation methods === | ||
| The accuracy of a quadrature rule of the ] type is generally a function of the number of evaluation points. The result is usually more accurate as the number of evaluation points increases, or, equivalently, as the width of the step size between the points decreases. It is natural to ask what the result would be if the step size were allowed to approach zero. This can be answered by extrapolating the result from two or more nonzero step sizes, using ] methods such as ]. The extrapolation function may be a ] or ]. Extrapolation methods are described in more detail by Stoer and Bulirsch (Section 3.4) and are implemented in many of the routines in the ] library. | |||
| The accuracy of a quadrature rule of the Newton-Cotes type is generally a function of the number of evaluation points. | |||
| The result is usually more accurate as number of evaluation points increases, | |||
| or, equivalently, as the width of the step size between the points decreases. | |||
| It is natural to ask what the result would be if the step size were allowed to approach zero. | |||
| This can be answered by extrapolating the result from two or more nonzero step sizes, using ] methods such as ]. | |||
| The extrapolation function may be a ] or ]. | |||
| Extrapolation methods are described in more detail by Stoer and Bulirsch (Section 3.4) and are implemented in many of the routines in the ] library. | |||
| === Conservative (a priori) error estimation === | === Conservative (a priori) error estimation === | ||
| Let <math>f</math> have a bounded first derivative over <math>,</math> i.e. <math>f \in C^1().</math> The ] for <math> f,</math> where <math>x \in [a,b),</math> gives | |||
| <math display="block"> (x - a) f'(\xi_x) = f(x) - f(a), </math> | |||
| for some <math> \xi_x \in (a,x] </math> depending on <math> x </math>. | |||
| If we integrate in <math> x </math> from <math> a </math> to <math> b </math> on both sides and take the absolute values, we obtain | |||
| Let ''f'' have a bounded first derivative over . The ] for ''f'', where ''x'' < ''b'', gives | |||
| <math display="block"> | |||
| \left| \int_a^b f(x)\, dx - (b - a) f(a) \right| | |||
| = \left| \int_a^b (x - a) f'(\xi_x)\, dx \right| . | |||
| </math> | |||
| We can further approximate the integral on the right-hand side by bringing the absolute value into the integrand, and replacing the term in <math> f' </math> by an upper bound | |||
| : <math>(x - a) f'(v_x) = f(x) - f(a)\,</math> | |||
| {{NumBlk|:| | |||
| <math> | |||
| \left| \int_a^b f(x)\, dx - (b - a) f(a) \right| | |||
| \leq {(b - a)^2 \over 2} \sup_{a \leq x \leq b} \left| f'(x) \right| , | |||
| </math> | |||
| |{{EquationRef|1}} | |||
| }} | |||
| where the ] was used to approximate. | |||
| Hence, if we approximate the integral <math display="inline"> \int_a^b f(x) \, dx </math> by the ] <math> (b - a) f(a) </math> our error is no greater than the right hand side of {{EquationNote|1}}. We can convert this into an error analysis for the ], giving an upper bound of | |||
| for some ''v<sub>x</sub>'' in depending on ''x''. If we integrate in ''x'' from ''a'' to ''b'' on both sides and take the absolute values, we obtain | |||
| <math display="block">\frac{n^{-1}}{2} \sup_{0 \leq x \leq 1} \left| f'(x) \right|</math> | |||
| for the error term of that particular approximation. (Note that this is precisely the error we calculated for the example <math>f(x) = x</math>.) Using more derivatives, and by tweaking the quadrature, we can do a similar error analysis using a ] (using a partial sum with remainder term) for ''f''. This error analysis gives a strict upper bound on the error, if the derivatives of ''f'' are available. | |||
| : <math>\left| \int_a^b f(x)\,dx - (b - a) f(a) \right| | |||
| = \left| \int_a^b (x - a) f'(v_x)\, dx \right|</math> | |||
| We can further approximate the integral on the right-hand side by bringing the absolute value into the integrand, and replacing the term in ''f' '' by an upper bound: | |||
| : <math>\left| \int_a^b f(x)\,dx - (b - a) f(a) \right| \leq {(b - a)^2 \over 2} \sup_{a \leq x \leq b} \left| f'(x) \right|</math> (**) | |||
| (See ].) Hence, if we approximate the integral ∫<sub>''a''</sub><sup>''b''</sup> ''f''(''x'') d''x'' by the quadrature rule (''b'' − ''a'')''f''(''a'') our error is no greater than the right hand side of (**). We can convert this into an error analysis for the Riemann sum (*), giving an upper bound of | |||
| : <math>{n^{-1} \over 2} \sup_{0 \leq x \leq 1} \left| f'(x) \right|</math> | |||
| for the ] of that particular approximation. (Note that this is precisely the error we calculated for the example <math>f(x) = x</math>.) Using more derivatives, and by tweaking the quadrature, we can do a similar error analysis using a ] (using a partial sum with remainder term) for ''f''. This error analysis gives a strict upper bound on the error, if the derivatives of ''f'' are available. | |||
| This integration method can be combined with ] to produce ]s and ''verified'' calculations. | This integration method can be combined with ] to produce ]s and ''verified'' calculations. | ||
| === Integrals over infinite intervals === | === Integrals over infinite intervals === | ||
| Several methods exist for approximate integration over unbounded intervals. The standard technique involves specially derived quadrature rules, such as ] for integrals on the whole real line and ] for integrals on the positive reals.<ref>{{cite book |last=Leader |first=Jeffery J. | author-link=Jeffery J. Leader| title=Numerical Analysis and Scientific Computation |year=2004 |publisher=Addison Wesley |isbn= 978-0-201-73499-7}}</ref> Monte Carlo methods can also be used, or a change of variables to a finite interval; e.g., for the whole line one could use | |||
| <math display="block"> | |||
| Several methods exist for approximate integration over unbounded intervals. The standard technique involves specially derived quadrature rules, such as ] for integrals on the whole real line and ] for integrals on the positive reals.<ref>{{cite book |last=Leader |first=Jeffery J. | authorlink=Jeffery J. Leader| title=Numerical Analysis and Scientific Computation |year=2004 |publisher=Addison Wesley |location= |isbn= 0-201-73499-0}}</ref> Monte Carlo methods can also be used, or a change of variables to a finite interval; e.g., for the whole line one could use | |||
| \int_{-\infty}^{\infty} f(x) \, dx | |||
| = \int_{-1}^{+1} f\left( \frac{t}{1-t^2} \right) \frac{1+t^2}{\left(1-t^2\right)^2} \, dt, | |||
| :<math> | |||
| \int_{-\infty}^{+\infty} f(x) \, dx = \int_{-1}^{+1} f\left( \frac{t}{1-t^2} \right) \frac{1+t^2}{(1-t^2)^2} \, dt, | |||
| </math> | </math> | ||
| and for semi-infinite intervals one could use | and for semi-infinite intervals one could use | ||
| <math display="block">\begin{align} | |||
| \int_a^{\infty} f(x) \, dx &= \int_0^1 f\left(a + \frac{t}{1-t}\right) \frac{dt}{(1-t)^2}, \\ | |||
| :<math> | |||
| \ |
\int_{-\infty}^a f(x) \, dx &= \int_0^1 f\left(a - \frac{1-t}{t}\right) \frac{dt}{t^2}, | ||
| \end{align}</math> | |||
| :<math> | |||
| \int_{-\infty}^a f(x) \, dx = \int_0^1 f\left(a - \frac{1-t}{t}\right) \frac{dt}{t^2}</math> | |||
| as possible transformations. | as possible transformations. | ||
| == Multidimensional integrals == | == Multidimensional integrals == | ||
| The quadrature rules discussed so far are all designed to compute one-dimensional integrals. To compute integrals in multiple dimensions, one approach is to phrase the multiple integral as repeated one-dimensional integrals by applying ] (the tensor product rule). This approach requires the function evaluations to ] as the number of dimensions increases. Three methods are known to overcome this so-called '']''. | |||
| A great many additional techniques for forming multidimensional cubature integration rules for a variety of weighting functions are given in the monograph by Stroud.<ref name="StroudBook">{{cite book |last1=Stroud |first1=A. H. |title=Approximate Calculation of Multiple Integrals |url=https://archive.org/details/approximatecalcu0000stro_b8j7 |url-access=registration |date=1971 |publisher=Prentice-Hall Inc. |location=Cliffs, NJ|isbn=9780130438935 }}</ref> | |||
| The quadrature rules discussed so far are all designed to compute one-dimensional integrals. | |||
| Integration on the ] has been reviewed by Hesse et al. (2015).<ref>Kerstin Hesse, Ian H. Sloan, and Robert S. Womersley: Numerical Integration on the Sphere. In W. Freeden et al. (eds.), Handbook of Geomathematics, Springer: Berlin 2015, {{doi|10.1007/978-3-642-54551-1_40}}</ref> | |||
| To compute integrals in multiple dimensions, | |||
| one approach is to phrase the multiple integral as repeated one-dimensional integrals by appealing to ]. | |||
| This approach requires the function evaluations to ] as the number of dimensions increases. Two methods are known to overcome this so-called '']''. | |||
| === Monte Carlo === | === Monte Carlo === | ||
| {{main|Monte Carlo integration}} | {{main|Monte Carlo integration}} | ||
| ]s and ]s are easy to apply to multi-dimensional integrals |
]s and ]s are easy to apply to multi-dimensional integrals. They may yield greater accuracy for the same number of function evaluations than repeated integrations using one-dimensional methods.{{Citation needed|date=November 2018}} | ||
| and may yield greater accuracy for the same number of function evaluations than repeated integrations using one-dimensional methods. | |||
| A large class of useful Monte Carlo methods are the so-called ] algorithms, | A large class of useful Monte Carlo methods are the so-called ] algorithms, which include the ] and ]. | ||
| which include the ] and ]. | |||
| === Sparse grids === | === Sparse grids === | ||
| ]s were originally developed by Smolyak for the quadrature of high |
]s were originally developed by Smolyak for the quadrature of high-dimensional functions. The method is always based on a one-dimensional quadrature rule, but performs a more sophisticated combination of univariate results. However, whereas the tensor product rule guarantees that the weights of all of the cubature points will be positive if the weights of the quadrature points were positive, Smolyak's rule does not guarantee that the weights will all be positive. | ||
| === Bayesian quadrature === | |||
| == Connection with differential equations == | |||
| ] is a statistical approach to the numerical problem of computing integrals and falls under the field of ]. It can provide a full handling of the uncertainty over the solution of the integral expressed as a ] posterior variance. | |||
| == Connection with differential equations == | |||
| The problem of evaluating the integral | |||
| The problem of evaluating the definite integral | |||
| :<math>F = \int_a^b f(x)\, dx</math> | |||
| :<math>F(x) = \int_a^x f(u)\, du</math> | |||
| can be reduced to an ] for an ]. If the above integral is denoted by ''F''(''x''), then the function ''F'' satisfies | |||
| can be reduced to an ] for an ] by applying the first part of the ]. By differentiating both sides of the above with respect to the argument ''x'', it is seen that the function ''F'' satisfies | |||
| :<math> \frac{d F(x)}{d x} = f(x), \quad F(a) = 0. </math> | :<math> \frac{d F(x)}{d x} = f(x), \quad F(a) = 0. </math> | ||
| Methods developed for ordinary differential equations, such as ], can be applied to the restated problem and thus be used to evaluate the integral. For instance, the standard fourth-order Runge–Kutta method applied to the differential equation yields Simpson's rule from above. | |||
| ], such as ], can be applied to the restated problem and thus be used to evaluate the integral. For instance, the standard fourth-order Runge–Kutta method applied to the differential equation yields Simpson's rule from above. | |||
| The differential equation ''F'' ' (''x'') = ƒ(''x'') has a special form: the right-hand side contains only the dependent variable (here ''x'') and not the independent variable (here ''F''). This simplifies the theory and algorithms considerably. The problem of evaluating integrals is thus best studied in its own right. | |||
| The differential equation <math>F'(x) = f(x)</math> has a special form: the right-hand side contains only the independent variable (here <math>x</math>) and not the dependent variable (here <math>F</math>). This simplifies the theory and algorithms considerably. The problem of evaluating integrals is thus best studied in its own right. | |||
| Conversely, the term "quadrature" may also be used for the solution of differential equations: "]" or "]" means expressing its solution in terms of ]. | |||
| ==See also== | ==See also== | ||
| * ] | |||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] or ] | * ] or ] | ||
| * ] | * ] | ||
| * ] | |||
| * ] | |||
| * ] | |||
| ==References== | ==References== | ||
| {{ |
{{Reflist}} | ||
| * ] and ], ''Methods of Numerical Integration''. | * ] and ], ''Methods of Numerical Integration''. | ||
| * ], Michael A. Malcolm, and ], ''Computer Methods for Mathematical Computations''. Englewood Cliffs, NJ: Prentice-Hall, 1977. ''(See Chapter |
* ], Michael A. Malcolm, and ], ''Computer Methods for Mathematical Computations''. Englewood Cliffs, NJ: Prentice-Hall, 1977. ''(See Chapter 5.)'' | ||
| * {{Citation |last1= |
* {{Citation |last1=Press |author-link=William H. Press |first1=W.H.|last2=Teukolsky|author2-link=Saul Teukolsky|first2=S.A.|last3=Vetterling|first3=W.T.|last4=Flannery|first4=B.P.|year=2007|title=Numerical Recipes: The Art of Scientific Computing|edition=3rd|publisher=Cambridge University Press| location=New York|isbn=978-0-521-88068-8|chapter=Chapter 4. Integration of Functions|chapter-url=http://apps.nrbook.com/empanel/index.html?pg=155}} | ||
| * ] and ], ''Introduction to Numerical Analysis''. New York: Springer-Verlag, 1980. ''(See Chapter 3.)'' | * ] and ], ''Introduction to Numerical Analysis''. New York: Springer-Verlag, 1980. ''(See Chapter 3.)'' | ||
| * ], ''A History of Mathematics'', 2nd ed. rev. by Uta C. Merzbach, New York: Wiley, 1989 |
* ], ''A History of Mathematics'', 2nd ed. rev. by ], New York: Wiley, 1989 {{isbn|0-471-09763-2}} (1991 pbk ed. {{isbn|0-471-54397-7}}). | ||
| * ], ''An Introduction to the History of Mathematics'', Saunders, 1990, |
* ], ''An Introduction to the History of Mathematics'', Saunders, 1990, {{isbn|0-03-029558-0}}, | ||
| * S.L.Sobolev and V.L.Vaskevich: ''The Theory of Cubature Formulas'', Kluwer Academic, ISBN 0-7923-4631-9 (1997). | |||
| ==External links== | ==External links== | ||
| {{commons category}} | |||
| * at Holistic Numerical Methods Institute | * at Holistic Numerical Methods Institute | ||
| * from Wolfram Mathworld | |||
| * from Encyclopedia of Mathematics | |||
| * within the free ]. | |||
| * | |||
| {{Numerical integration}} | |||
| {{Differential equations topics}} | |||
| {{Authority control}} | |||
| Numerical integration is one of the most intensively studied problems in numerical analysis. | |||
| Of the many software implementations, we list a few ] packages here: | |||
| * ] (part of SLATEC): description , source code . QUADPACK is a collection of algorithms, in Fortran, for numerical integration based on Gaussian quadrature. | |||
| * : a solver from ]/] frameworks, based on interval analysis, guaranteed precision, license: BSD (free for any purposes) | |||
| * : The GNU Scientific Library (GSL) is a numerical library written in C that provides a wide range of mathematical routines, like Monte Carlo integration. | |||
| * Numerical integration algorithms are found in ] class . | |||
| * is a collection of algorithms, in C# / C++ / Delphi / Visual Basic / etc., for numerical integration (includes Bulirsch-Stoer and Runge-Kutta integrators). | |||
| * is a free-software library of several multi-dimensional integration algorithms. | |||
| * code for adaptive multi-dimensional integration. | |||
| * is an open source software under CeCILL license (GPL compatible), providing powerful features including numerical integration. | |||
| ] | ] | ||
| ] | ] | ||
| ] | |||
Latest revision as of 17:45, 24 October 2024
Methods of calculating definite integrals
| Differential equations | ||||||
|---|---|---|---|---|---|---|
| Scope | ||||||
Fields
List of named differential equations |
||||||
| Classification | ||||||
Types
|
||||||
| Relation to processes | ||||||
| Solution | ||||||
| Existence and uniqueness | ||||||
| General topics | ||||||
| Solution methods | ||||||
| People | ||||||
| List | ||||||
In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral. The term numerical quadrature (often abbreviated to quadrature) is more or less a synonym for "numerical integration", especially as applied to one-dimensional integrals. Some authors refer to numerical integration over more than one dimension as cubature; others take "quadrature" to include higher-dimensional integration.
The basic problem in numerical integration is to compute an approximate solution to a definite integral
to a given degree of accuracy. If f(x) is a smooth function integrated over a small number of dimensions, and the domain of integration is bounded, there are many methods for approximating the integral to the desired precision.
Numerical integration has roots in the geometrical problem of finding a square with the same area as a given plane figure (quadrature or squaring), as in the quadrature of the circle. The term is also sometimes used to describe the numerical solution of differential equations.
Motivation and need
There are several reasons for carrying out numerical integration, as opposed to analytical integration by finding the antiderivative:
- The integrand f (x) may be known only at certain points, such as obtained by sampling. Some embedded systems and other computer applications may need numerical integration for this reason.
- A formula for the integrand may be known, but it may be difficult or impossible to find an antiderivative that is an elementary function. An example of such an integrand is f (x) = exp(−x), the antiderivative of which (the error function, times a constant) cannot be written in elementary form. See also: nonelementary integral
- It may be possible to find an antiderivative symbolically, but it may be easier to compute a numerical approximation than to compute the antiderivative. That may be the case if the antiderivative is given as an infinite series or product, or if its evaluation requires a special function that is not available.
History
Main article: Quadrature (mathematics)The term "numerical integration" first appears in 1915 in the publication A Course in Interpolation and Numeric Integration for the Mathematical Laboratory by David Gibb.
"Quadrature" is a historical mathematical term that means calculating area. Quadrature problems have served as one of the main sources of mathematical analysis. Mathematicians of Ancient Greece, according to the Pythagorean doctrine, understood calculation of area as the process of constructing geometrically a square having the same area (squaring). That is why the process was named "quadrature". For example, a quadrature of the circle, Lune of Hippocrates, The Quadrature of the Parabola. This construction must be performed only by means of compass and straightedge.
The ancient Babylonians used the trapezoidal rule to integrate the motion of Jupiter along the ecliptic.
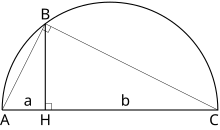
For a quadrature of a rectangle with the sides a and b it is necessary to construct a square with the side (the Geometric mean of a and b). For this purpose it is possible to use the following fact: if we draw the circle with the sum of a and b as the diameter, then the height BH (from a point of their connection to crossing with a circle) equals their geometric mean. The similar geometrical construction solves a problem of a quadrature for a parallelogram and a triangle.

Problems of quadrature for curvilinear figures are much more difficult. The quadrature of the circle with compass and straightedge had been proved in the 19th century to be impossible. Nevertheless, for some figures (for example the Lune of Hippocrates) a quadrature can be performed. The quadratures of a sphere surface and a parabola segment done by Archimedes became the highest achievement of the antique analysis.
- The area of the surface of a sphere is equal to quadruple the area of a great circle of this sphere.
- The area of a segment of the parabola cut from it by a straight line is 4/3 the area of the triangle inscribed in this segment.
For the proof of the results Archimedes used the Method of exhaustion of Eudoxus.
In medieval Europe the quadrature meant calculation of area by any method. More often the Method of indivisibles was used; it was less rigorous, but more simple and powerful. With its help Galileo Galilei and Gilles de Roberval found the area of a cycloid arch, Grégoire de Saint-Vincent investigated the area under a hyperbola (Opus Geometricum, 1647), and Alphonse Antonio de Sarasa, de Saint-Vincent's pupil and commentator, noted the relation of this area to logarithms.
John Wallis algebrised this method: he wrote in his Arithmetica Infinitorum (1656) series that we now call the definite integral, and he calculated their values. Isaac Barrow and James Gregory made further progress: quadratures for some algebraic curves and spirals. Christiaan Huygens successfully performed a quadrature of some Solids of revolution.
The quadrature of the hyperbola by Saint-Vincent and de Sarasa provided a new function, the natural logarithm, of critical importance.
With the invention of integral calculus came a universal method for area calculation. In response, the term "quadrature" has become traditional, and instead the modern phrase "computation of a univariate definite integral" is more common.
Methods for one-dimensional integrals
A quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration.
Numerical integration methods can generally be described as combining evaluations of the integrand to get an approximation to the integral. The integrand is evaluated at a finite set of points called integration points and a weighted sum of these values is used to approximate the integral. The integration points and weights depend on the specific method used and the accuracy required from the approximation.
An important part of the analysis of any numerical integration method is to study the behavior of the approximation error as a function of the number of integrand evaluations. A method that yields a small error for a small number of evaluations is usually considered superior. Reducing the number of evaluations of the integrand reduces the number of arithmetic operations involved, and therefore reduces the total error. Also, each evaluation takes time, and the integrand may be arbitrarily complicated.
Quadrature rules based on step functions
A "brute force" kind of numerical integration can be done, if the integrand is reasonably well-behaved (i.e. piecewise continuous and of bounded variation), by evaluating the integrand with very small increments.

This simplest method approximates the function by a step function (a piecewise constant function, or a segmented polynomial of degree zero) that passes through the point . This is called the midpoint rule or rectangle rule
Quadrature rules based on interpolating functions
A large class of quadrature rules can be derived by constructing interpolating functions that are easy to integrate. Typically these interpolating functions are polynomials. In practice, since polynomials of very high degree tend to oscillate wildly, only polynomials of low degree are used, typically linear and quadratic.

The interpolating function may be a straight line (an affine function, i.e. a polynomial of degree 1) passing through the points and . This is called the trapezoidal rule
For either one of these rules, we can make a more accurate approximation by breaking up the interval into some number of subintervals, computing an approximation for each subinterval, then adding up all the results. This is called a composite rule, extended rule, or iterated rule. For example, the composite trapezoidal rule can be stated as
where the subintervals have the form with and Here we used subintervals of the same length but one could also use intervals of varying length .
Interpolation with polynomials evaluated at equally spaced points in yields the Newton–Cotes formulas, of which the rectangle rule and the trapezoidal rule are examples. Simpson's rule, which is based on a polynomial of order 2, is also a Newton–Cotes formula.
Quadrature rules with equally spaced points have the very convenient property of nesting. The corresponding rule with each interval subdivided includes all the current points, so those integrand values can be re-used.
If we allow the intervals between interpolation points to vary, we find another group of quadrature formulas, such as the Gaussian quadrature formulas. A Gaussian quadrature rule is typically more accurate than a Newton–Cotes rule that uses the same number of function evaluations, if the integrand is smooth (i.e., if it is sufficiently differentiable). Other quadrature methods with varying intervals include Clenshaw–Curtis quadrature (also called Fejér quadrature) methods, which do nest.
Gaussian quadrature rules do not nest, but the related Gauss–Kronrod quadrature formulas do.
Adaptive algorithms
This section is an excerpt from Adaptive quadrature. Adaptive quadrature is a numerical integration method in which the integral of a function is approximated using static quadrature rules on adaptively refined subintervals of the region of integration. Generally, adaptive algorithms are just as efficient and effective as traditional algorithms for "well behaved" integrands, but are also effective for "badly behaved" integrands for which traditional algorithms may fail.Extrapolation methods
The accuracy of a quadrature rule of the Newton–Cotes type is generally a function of the number of evaluation points. The result is usually more accurate as the number of evaluation points increases, or, equivalently, as the width of the step size between the points decreases. It is natural to ask what the result would be if the step size were allowed to approach zero. This can be answered by extrapolating the result from two or more nonzero step sizes, using series acceleration methods such as Richardson extrapolation. The extrapolation function may be a polynomial or rational function. Extrapolation methods are described in more detail by Stoer and Bulirsch (Section 3.4) and are implemented in many of the routines in the QUADPACK library.
Conservative (a priori) error estimation
Let have a bounded first derivative over i.e. The mean value theorem for where gives for some depending on .
If we integrate in from to on both sides and take the absolute values, we obtain
We can further approximate the integral on the right-hand side by bringing the absolute value into the integrand, and replacing the term in by an upper bound
|
| (1) |
where the supremum was used to approximate.
Hence, if we approximate the integral by the quadrature rule our error is no greater than the right hand side of 1. We can convert this into an error analysis for the Riemann sum, giving an upper bound of for the error term of that particular approximation. (Note that this is precisely the error we calculated for the example .) Using more derivatives, and by tweaking the quadrature, we can do a similar error analysis using a Taylor series (using a partial sum with remainder term) for f. This error analysis gives a strict upper bound on the error, if the derivatives of f are available.
This integration method can be combined with interval arithmetic to produce computer proofs and verified calculations.
Integrals over infinite intervals
Several methods exist for approximate integration over unbounded intervals. The standard technique involves specially derived quadrature rules, such as Gauss-Hermite quadrature for integrals on the whole real line and Gauss-Laguerre quadrature for integrals on the positive reals. Monte Carlo methods can also be used, or a change of variables to a finite interval; e.g., for the whole line one could use and for semi-infinite intervals one could use as possible transformations.
Multidimensional integrals
The quadrature rules discussed so far are all designed to compute one-dimensional integrals. To compute integrals in multiple dimensions, one approach is to phrase the multiple integral as repeated one-dimensional integrals by applying Fubini's theorem (the tensor product rule). This approach requires the function evaluations to grow exponentially as the number of dimensions increases. Three methods are known to overcome this so-called curse of dimensionality.
A great many additional techniques for forming multidimensional cubature integration rules for a variety of weighting functions are given in the monograph by Stroud. Integration on the sphere has been reviewed by Hesse et al. (2015).
Monte Carlo
Main article: Monte Carlo integrationMonte Carlo methods and quasi-Monte Carlo methods are easy to apply to multi-dimensional integrals. They may yield greater accuracy for the same number of function evaluations than repeated integrations using one-dimensional methods.
A large class of useful Monte Carlo methods are the so-called Markov chain Monte Carlo algorithms, which include the Metropolis–Hastings algorithm and Gibbs sampling.
Sparse grids
Sparse grids were originally developed by Smolyak for the quadrature of high-dimensional functions. The method is always based on a one-dimensional quadrature rule, but performs a more sophisticated combination of univariate results. However, whereas the tensor product rule guarantees that the weights of all of the cubature points will be positive if the weights of the quadrature points were positive, Smolyak's rule does not guarantee that the weights will all be positive.
Bayesian quadrature
Bayesian quadrature is a statistical approach to the numerical problem of computing integrals and falls under the field of probabilistic numerics. It can provide a full handling of the uncertainty over the solution of the integral expressed as a Gaussian process posterior variance.
Connection with differential equations
The problem of evaluating the definite integral
can be reduced to an initial value problem for an ordinary differential equation by applying the first part of the fundamental theorem of calculus. By differentiating both sides of the above with respect to the argument x, it is seen that the function F satisfies
Numerical methods for ordinary differential equations, such as Runge–Kutta methods, can be applied to the restated problem and thus be used to evaluate the integral. For instance, the standard fourth-order Runge–Kutta method applied to the differential equation yields Simpson's rule from above.
The differential equation has a special form: the right-hand side contains only the independent variable (here ) and not the dependent variable (here ). This simplifies the theory and algorithms considerably. The problem of evaluating integrals is thus best studied in its own right.
Conversely, the term "quadrature" may also be used for the solution of differential equations: "solving by quadrature" or "reduction to quadrature" means expressing its solution in terms of integrals.
See also
- Truncation error (numerical integration)
- Clenshaw–Curtis quadrature
- Gauss-Kronrod quadrature
- Riemann Sum or Riemann Integral
- Trapezoidal rule
- Romberg's method
- Tanh-sinh quadrature
- Nonelementary Integral
References
- Weisstein, Eric W. "Cubature". MathWorld.
- "Earliest Known Uses of Some of the Words of Mathematics (Q)". jeff560.tripod.com. Retrieved 31 March 2018.
- Mathieu Ossendrijver (Jan 29, 2016). "Ancient Babylonian astronomers calculated Jupiter's position from the area under a time-velocity graph". Science. 351 (6272): 482–484. Bibcode:2016Sci...351..482O. doi:10.1126/science.aad8085. PMID 26823423. S2CID 206644971.
- Leader, Jeffery J. (2004). Numerical Analysis and Scientific Computation. Addison Wesley. ISBN 978-0-201-73499-7.
- Stroud, A. H. (1971). Approximate Calculation of Multiple Integrals. Cliffs, NJ: Prentice-Hall Inc. ISBN 9780130438935.
- Kerstin Hesse, Ian H. Sloan, and Robert S. Womersley: Numerical Integration on the Sphere. In W. Freeden et al. (eds.), Handbook of Geomathematics, Springer: Berlin 2015, doi:10.1007/978-3-642-54551-1_40
- Philip J. Davis and Philip Rabinowitz, Methods of Numerical Integration.
- George E. Forsythe, Michael A. Malcolm, and Cleve B. Moler, Computer Methods for Mathematical Computations. Englewood Cliffs, NJ: Prentice-Hall, 1977. (See Chapter 5.)
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007), "Chapter 4. Integration of Functions", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Josef Stoer and Roland Bulirsch, Introduction to Numerical Analysis. New York: Springer-Verlag, 1980. (See Chapter 3.)
- Boyer, C. B., A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach, New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7).
- Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0,
- S.L.Sobolev and V.L.Vaskevich: The Theory of Cubature Formulas, Kluwer Academic, ISBN 0-7923-4631-9 (1997).
External links
- Integration: Background, Simulations, etc. at Holistic Numerical Methods Institute
- Lobatto Quadrature from Wolfram Mathworld
- Lobatto quadrature formula from Encyclopedia of Mathematics
- Implementations of many quadrature and cubature formulae within the free Tracker Component Library.
- SageMath Online Integrator
| Numerical integration | |
|---|---|
| Newton–Cotes formulas | |
| Gaussian quadrature | |
| Other | |
| Differential equations | |||||||
|---|---|---|---|---|---|---|---|
| Classification |
| ||||||
| Solutions | |||||||
| Examples | |||||||
| Mathematicians | |||||||
 , the area under the curve defined by
, the area under the curve defined by  .
.
 (the
(the  . This is called the midpoint rule or
. This is called the midpoint rule or 
 and
and  .
This is called the
.
This is called the 
 into some number
into some number  of subintervals, computing an approximation for each subinterval, then adding up all the results. This is called a composite rule, extended rule, or iterated rule. For example, the composite trapezoidal rule can be stated as
of subintervals, computing an approximation for each subinterval, then adding up all the results. This is called a composite rule, extended rule, or iterated rule. For example, the composite trapezoidal rule can be stated as

 with
with  and
and  Here we used subintervals of the same length
Here we used subintervals of the same length  but one could also use intervals of varying length
but one could also use intervals of varying length  .
.
 have a bounded first derivative over
have a bounded first derivative over  i.e.
i.e.  The
The  where
where  gives
gives
 for some
for some ![{\displaystyle \xi _{x}\in (a,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8de63768671d262e845028640fc3a7255e6f6b6c) depending on
depending on  .
.
 to
to  on both sides and take the absolute values, we obtain
on both sides and take the absolute values, we obtain

 by an upper bound
by an upper bound

 by the
by the  our error is no greater than the right hand side of
our error is no greater than the right hand side of  for the error term of that particular approximation. (Note that this is precisely the error we calculated for the example
for the error term of that particular approximation. (Note that this is precisely the error we calculated for the example  .) Using more derivatives, and by tweaking the quadrature, we can do a similar error analysis using a
.) Using more derivatives, and by tweaking the quadrature, we can do a similar error analysis using a  and for semi-infinite intervals one could use
and for semi-infinite intervals one could use
 as possible transformations.
as possible transformations.


 has a special form: the right-hand side contains only the independent variable (here
has a special form: the right-hand side contains only the independent variable (here  ). This simplifies the theory and algorithms considerably. The problem of evaluating integrals is thus best studied in its own right.
). This simplifies the theory and algorithms considerably. The problem of evaluating integrals is thus best studied in its own right.