| Revision as of 12:38, 29 February 2016 editTrappist the monk (talk | contribs)Administrators479,973 editsm →Duodecimal digits on computerized writing systems: crudely translate Internetquelle to cite web; using AWB← Previous edit | Latest revision as of 06:51, 11 January 2025 edit undoThelurkingeditor (talk | contribs)46 edits →In media: rewrote for clarity, corrected punctuation and grammarTag: Visual edit | ||
| Line 1: | Line 1: | ||
| {{Short description|Base-12 numeral system}} | |||
| {{distinguish|Dewey Decimal Classification}} | |||
| {{distinguish|Dewey Decimal Classification|Duodecimo}} | |||
| {{Special characters}} | |||
| {{Numeral systems}} | {{Numeral systems}} | ||
| The '''duodecimal''' system |
The '''duodecimal''' system, also known as '''base twelve''' or '''dozenal''', is a ] ] using ] as its ]. In duodecimal, the number twelve is denoted "10", meaning 1 twelve and 0 ]; in the ] system, this number is instead written as "12" meaning 1 ten and 2 units, and the string "10" means ten. In duodecimal, "100" means twelve ], "1000" means twelve ], and "0.1" means a twelfth. | ||
| | url = http://www.unicode.org/charts/PDF/U2150.pdf | |||
| | title = The Unicode Standard 8.0 | |||
| | accessdate = 2014-07-18 | |||
| }}</ref> Other notations use "A", "T", or "X" for ten and "B" or "E" for eleven. The number twelve (that is, the number written as "12" in the ] numerical system) is instead written as "10" in duodecimal (meaning "1 ] and 0 units", instead of "1 ten and 0 units"), whereas the digit string "12" means "1 dozen and 2 units" (i.e. the same number that in decimal is written as "14"). Similarly, in duodecimal "100" means "1 ]", "1000" means "1 ]", and "0.1" means "1 twelfth" (instead of their decimal meanings "1 hundred", "1 thousand", and "1 tenth"). | |||
| Various symbols have been used to stand for ten and eleven in duodecimal notation; this page uses {{d2}} and {{d3}}, as in ], which make a duodecimal count from zero to twelve read 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, {{d2}}, {{d3}}, 10. The Dozenal Societies of America and Great Britain (organisations promoting the use of duodecimal) use turned digits in their published material: <span style="display: inline-block; transform: scale(-1);">2</span> (a turned 2) for ten and <span style="display: inline-block; transform: scale(-1);">3</span> (a turned 3) for eleven. | |||
| The number twelve, a ], is the smallest number with four non-trivial ] (2, 3, 4, 6), and the smallest to include as factors all four numbers (1 to 4) within the ] range. As a result of this increased factorability of the ] and its divisibility by a wide range of the most elemental numbers (whereas ten has only two non-trivial factors: 2 and 5, and not 3, 4, or 6), duodecimal representations fit more easily than decimal ones into many common patterns, as evidenced by the higher regularity observable in the duodecimal multiplication table. As a result, duodecimal has been described as the optimal number system.<ref>{{cite web | |||
| | url = http://io9.com/5977095/why-we-should-switch-to-a-base+12-counting-system | |||
| The number twelve, a ], is the smallest number with four non-trivial ] (2, 3, 4, 6), and the smallest to include as factors all four numbers (1 to 4) within the ] range, and the smallest ]. All multiples of ] of ] numbers ({{math|{{sfrac|''a''|2<sup>''b''</sup>·3<sup>''c''</sup>}}}} where {{mvar|a,b,c}} are integers) have a ] representation in duodecimal. In particular, {{sfrac||1|4}} (0.3), {{sfrac||1|3}} (0.4), {{sfrac||1|2}} (0.6), {{sfrac||2|3}} (0.8), and {{sfrac||3|4}} (0.9) all have a short terminating representation in duodecimal. There is also higher regularity observable in the duodecimal multiplication table. As a result, duodecimal has been described as the optimal number system.<ref name="io9">{{cite web |author=Dvorsky |first=George |date=January 18, 2013 |title=Why We Should Switch To A Base-12 Counting System |url=http://io9.com/5977095/why-we-should-switch-to-a-base+12-counting-system |access-date=December 21, 2013 |website=]}}</ref> | |||
| | title = Why We Should Switch To A Base-12 Counting System | |||
| | author = George Dvorsky | |||
| In these respects, duodecimal is considered superior to decimal, which has only 2 and 5 as factors, and other proposed bases like ] or ]. ] (base sixty) does even better in this respect (the reciprocals of all ] numbers terminate), but at the cost of unwieldy multiplication tables and a much larger number of symbols to memorize. | |||
| | date = 2013-01-18 | |||
| | accessdate = 2013-12-21 | |||
| }}</ref> Of its factors, 2 and 3 are ], which means the ] of all ] numbers (such as 2, 3, 4, 6, 8, 9...) have a ] representation in duodecimal. In particular, the five most elementary fractions ({{sfrac|1|2}}, {{sfrac|1|3}}, {{sfrac|2|3}}, {{sfrac|1|4}} and {{sfrac|3|4}}) all have a short terminating representation in duodecimal (0.6, 0.4, 0.8, 0.3 and 0.9, respectively), and twelve is the smallest radix with this feature (because it is the ] of 3 and 4). This all makes it a more convenient number system for computing fractions than most other number systems in common use, such as the ], ], ], ] and ] systems. Although the ] and ] systems (where the reciprocals of all ] numbers terminate) do even better in this respect, this is at the cost of unwieldy multiplication tables and a much larger number of symbols to memorize. | |||
| == Origin == | == Origin == | ||
| :''In this section, numerals are |
:''In this section, numerals are in ]. For example, "10" means 9+1, and "12" means 9+3.'' | ||
| ] speculatively traced the origin of the duodecimal system to a system of ] based on the knuckle bones of the four larger fingers. Using the thumb as a pointer, it is possible to count to 12 by touching each finger bone, starting with the farthest bone on the fifth finger, and counting on. In this system, one hand counts repeatedly to 12, while the other displays the number of iterations, until five dozens, i.e. the 60, are full. This system is still in use in many regions of Asia.<ref>{{cite journal |last=Pittman |first=Richard |date=1990 |title=Origin of Mesopotamian duodecimal and sexagesimal counting systems |journal=Philippine Journal of Linguistics |volume=21 |issue=1 |page=97}}</ref><ref name="Ifrah 2000">{{Cite book| last = Ifrah| first = Georges| author-link = Georges Ifrah| title = The Universal History of Numbers: From prehistory to the invention of the computer| publisher = Wiley | year=2000 |orig-year=1st French ed. 1981 | isbn = 0-471-39340-1}} Translated from the French by David Bellos, E. F. Harding, Sophie Wood and Ian Monk.</ref> | |||
| Languages using duodecimal number systems are uncommon. Languages in the ]n Middle Belt such as ], ] (Gure-Kahugu), ], and the Nimbia dialect of ];<ref>{{Cite |
Languages using duodecimal number systems are uncommon. Languages in the ]n Middle Belt such as ], ] (Gure-Kahugu), ], and the Nimbia dialect of ];<ref>{{Cite web |last=Matsushita |first=Shuji |date=October 1998 |title=Decimal vs. Duodecimal: An interaction between two systems of numeration |url=http://www3.aa.tufs.ac.jp/~P_aflang/TEXTS/oct98/decimal.html |url-status=dead |archive-url=https://web.archive.org/web/20081005230737/http://www3.aa.tufs.ac.jp/~P_aflang/TEXTS/oct98/decimal.html |archive-date=October 5, 2008 |access-date=May 29, 2011 |website=www3.aa.tufs.ac.jp}}</ref> and the ] of ]<ref>{{Cite book | ||
| | title=Decimal vs. Duodecimal: An interaction between two systems of numeration | |||
| | last=Matsushita | |||
| | first=Shuji | |||
| | conference=2nd Meeting of the AFLANG, October 1998, Tokyo | |||
| | year=1998 | |||
| | url=http://www3.aa.tufs.ac.jp/~P_aflang/TEXTS/oct98/decimal.html | |||
| | archiveurl=http://web.archive.org/web/20081005230737/http://www3.aa.tufs.ac.jp/~P_aflang/TEXTS/oct98/decimal.html | |||
| | archivedate=2008-10-05 | |||
| | accessdate=2011-05-29 | |||
| | postscript=<!-- Bot inserted parameter. Either remove it; or change its value to "." for the cite to end in a ".", as necessary. -->{{inconsistent citations}} | |||
| }}</ref> the ] of ]<ref>{{Cite book | |||
| | contribution=Les principes de construction du nombre dans les langues tibéto-birmanes | | contribution=Les principes de construction du nombre dans les langues tibéto-birmanes | ||
| | first=Martine | | first=Martine | ||
| Line 37: | Line 22: | ||
| | editor-first=Jacques | | editor-first=Jacques | ||
| | editor-last=François | | editor-last=François | ||
| | |
| date=2002 | ||
| | pages=91–119 | | pages=91–119 | ||
| | publisher=Peeters | | publisher=Peeters | ||
| Line 43: | Line 28: | ||
| | isbn=90-429-1295-2 | | isbn=90-429-1295-2 | ||
| | url=http://lacito.vjf.cnrs.fr/documents/publi/num_WEB.pdf | | url=http://lacito.vjf.cnrs.fr/documents/publi/num_WEB.pdf | ||
| | access-date=2014-03-27 | |||
| | postscript=<!-- Bot inserted parameter. Either remove it; or change its value to "." for the cite to end in a ".", as necessary. -->{{inconsistent citations}} | |||
| | archive-date=2016-03-28 | |||
| }}</ref> and the ] of ] in ] are known to use duodecimal numerals. In fiction, ]'s ] can express numbers either decimally (in ], ''maquanótië'' "hand-counting" or *''quaistanótië'' "tenth-counting") or duodecimally (presumably *''rastanótië'' "dozen-counting").<ref>{{cite journal|last1=Tolkien|first1=Christopher|last2=Tolkien|first2=John|editor1-last=Doughan|editor1-first=David|editor2-last=Julian|editor2-first=Bradfiend|title=The Writing Systems of Middle-earth|journal=Quetters|date=1987|volume=Special Publication|issue=1|url=http://tolklang.quettar.org/numbers.ps|postscript=<!--I can't upload image file "http://elvenesse.net/blog/wp-content/uploads/2012/02/ElvishNoChart.jpg"-->}}</ref> | |||
| | archive-url=https://web.archive.org/web/20160328145817/http://lacito.vjf.cnrs.fr/documents/publi/num_WEB.pdf | |||
| | url-status=dead | |||
| }}</ref> are known to use duodecimal numerals. | |||
| ] have special words for 11 and 12, such as ''eleven'' and ''twelve'' in ]. |
] have special words for 11 and 12, such as ''eleven'' and ''twelve'' in ]. They come from ] *''ainlif'' and *''twalif'' (meaning, respectively, ''one left'' and ''two left''), suggesting a decimal rather than duodecimal origin.<ref>{{cite book|last=von Mengden| first=Ferdinand| date=2006|chapter=The peculiarities of the Old English numeral system |title=Medieval English and its Heritage: Structure Meaning and Mechanisms of Change|editor1=Nikolaus Ritt |editor2=Herbert Schendl |editor3=Christiane Dalton-Puffer |editor4=Dieter Kastovsky|publisher=Peter Lang |series=Studies in English Medieval Language and Literature |volume=16 |location=Frankfurt |pages= 125–145}}</ref><ref>{{cite book|last=von Mengden |first=Ferdinand |date=2010| title=Cardinal Numerals: Old English from a Cross-Linguistic Perspective |series=Topics in English Linguistics | volume=67|location= Berlin; New York|publisher=De Gruyter Mouton| pages=159–161}}</ref> However, ] used a hybrid decimal–duodecimal counting system, with its words for "one hundred and eighty" meaning 200 and "two hundred" meaning 240.<ref>{{cite book|last=Gordon|first=E V|title=Introduction to Old Norse|year=1957|publisher=Clarendon Press|location=Oxford|pages=292–293}}</ref> In the British Isles, this style of counting survived well into the Middle Ages as the ]. | ||
| Historically, ] of |
Historically, ] in many ]s are duodecimal. There are twelve signs of the ], twelve months in a year, and the ] had twelve hours in a day (although at some point, this was changed to 24). Traditional ]s, clocks, and compasses are based on the twelve ] or 24 (12×2) ]s. There are 12 inches in an imperial foot, 12 ] ounces in a troy pound, 12 ] in a ], 24 (12×2) hours in a day; many other items are counted by the ], ] (], ] of 12), or ] (], ] of 12). The Romans used a fraction system based on 12, including the ], which became both the English words '']'' and ''inch''. Pre-], ] and the ] used a mixed duodecimal-] currency system (12 pence = 1 shilling, 20 shillings or 240 pence to the ] or ]), and ] established a monetary system that also had a mixed base of twelve and twenty, the remnants of which persist in many places. | ||
| {| class="wikitable" style=text-align:center | {| class="wikitable" style=text-align:center | ||
| |+ Duodecimally divided units | |||
| ! colspan="6"|<big>Table of units from a base of 12</big> | |||
| |- | |- | ||
| ! Relative<br>value | ! rowspan=2 | Relative<br>value | ||
| ! colspan=2 | Length | |||
| ! French unit<br>of length | |||
| ! colspan=2 | Weight | |||
| ! English unit<br>of length | |||
| |- | |||
| ! English unit<br>of weight | |||
| ! French | |||
| ! Roman unit<br>of weight | |||
| ! English |
! English | ||
| ! English (Troy) | |||
| ! Roman | |||
| |- | |- | ||
| |12<sup>0</sup> | |12<sup>0</sup> | ||
| Line 66: | Line 55: | ||
| |] | |] | ||
| |] | |] | ||
| | | |||
| |- | |- | ||
| |12<sup>−1</sup> | |12<sup>−1</sup> | ||
| Line 73: | Line 61: | ||
| |] | |] | ||
| |] | |] | ||
| |] | |||
| |- | |- | ||
| |12<sup>−2</sup> | |12<sup>−2</sup> | ||
| Line 79: | Line 66: | ||
| |] | |] | ||
| |2 ] | |2 ] | ||
| |2 ] | |2 ] | ||
| |] | |||
| |- | |- | ||
| |12<sup>−3</sup> | |12<sup>−3</sup> | ||
| Line 86: | Line 72: | ||
| |] | |] | ||
| |] | |] | ||
| |] |
|] | ||
| |} | |||
| == Notations and pronunciations == | |||
| In a positional numeral system of base ''n'' (twelve for duodecimal), each of the first ''n'' natural numbers is given a distinct numeral symbol, and then ''n'' is denoted "10", meaning 1 times ''n'' plus 0 units. For duodecimal, the standard numeral symbols for 0–9 are typically preserved for zero through nine, but there are numerous proposals for how to write the numerals representing "ten" and "eleven".<ref name="Symbology Overview">{{cite journal|last=De Vlieger|first=Michael|title=Symbology Overview|journal=The Duodecimal Bulletin|volume=4X |issue=2|date=2010|url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue4a2_0.pdf }}</ref> More radical proposals do not use any ] under the principle of "separate identity."<ref name="Symbology Overview" /> | |||
| Pronunciation of duodecimal numbers also has no standard, but various systems have been proposed. | |||
| === Transdecimal symbols === | |||
| {{infobox symbol | |||
| |mark={{mono|1=<span style="display: inline-block; transform: scale(-1);">2</span>{{NBSP}}<span style="display: inline-block; transform: scale(-1);">3</span>}} | |||
| |name = duodecimal {{angbr|1=ten, eleven}} | |||
| |unicode={{ubli | |||
| | {{unichar|1=218A|2=TURNED DIGIT TWO}} | |||
| | {{unichar|1=218B|2=TURNED DIGIT THREE}} | |||
| }} | |||
| |unicode note=Block ] | |||
| |note={{ubli | |||
| |Arabic digits with 180° rotation, by ] | |||
| |In ], using the TIPA package:<ref name="LATEX">{{cite web |url=https://www.ctan.org/pkg/comprehensive |title=The Comprehensive LATEX Symbol List |year=2021 |edition=14.0 |orig-year=2007 |last=Pakin |first=Scott |website=Comprehensive TEX Archive Network }} {{pb}} {{cite web |url=https://www.ctan.org/pkg/tipa |title=tipa – Fonts and macros for IPA phonetics characters |last=Rei |first=Fukui |year=2004 |orig-year=2002 |website=Comprehensive TEX Archive Network |edition=1.3 }} {{pb}} The turned digits 2 and 3 employed in the TIPA package originated in ''The Principles of the International Phonetic Association'', University College London, 1949.</ref><br/>{{angbr|1={{code|\textturntwo}}, {{code|1=\textturnthree}}}}}} | |||
| }} | |||
| Several authors have proposed using letters of the alphabet for the transdecimal symbols. Latin letters such as {{angbr|{{mono|1=A, B}}}} (as in ]) or {{angbr|{{mono|1=T, E}}}} (initials of ''Ten'' and ''Eleven'') are convenient because they are widely accessible, and for instance can be typed on typewriters. However, when mixed with ordinary prose, they might be confused for letters. As an alternative, Greek letters such as {{angbr|{{mono|1=τ, ε}}}} could be used instead.<ref name="Symbology Overview"/> Frank Emerson Andrews, an early American advocate for duodecimal, suggested and used in his 1935 book ''New Numbers'' {{angbr|{{mono|''X'', ''Ɛ''}}}} (italic capital X from the ] for ten and a rounded ] capital E similar to ]), along with italic numerals {{mono|''0''}}–{{mono|''9''}}.<ref name="New Numbers 1935"/> | |||
| Edna Kramer in her 1951 book ''The Main Stream of Mathematics'' used a {{angbr|{{mono|1=*, <nowiki>#</nowiki>}}}} (] or six-pointed asterisk, ] or octothorpe).<ref name="Symbology Overview"/> The symbols were chosen because they were available on some typewriters; they are also on ]s.<ref name="Symbology Overview"/> This notation was used in publications of the Dozenal Society of America (DSA) from 1974 to 2008.<ref>{{cite journal|title=Annual Meeting of 1973 and Meeting of the Board|journal=The Duodecimal Bulletin|volume=25 |issue=1|date=1974|url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue251-web_0.pdf}}</ref><ref>{{cite journal|last=De Vlieger|first=Michael|title=Going Classic|journal=The Duodecimal Bulletin|volume=49 |issue=2|date=2008|url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue492_0.pdf}}</ref> | |||
| From 2008 to 2015, the DSA used {{angbr|1={{NNBSP}}], ]{{NNBSP}}}}, the symbols devised by ].<ref name="Symbology Overview"/><ref name="DB01">{{cite journal|title=Mo for Megro|journal=The Duodecimal Bulletin|volume=1|issue=1|date=1945|url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue011-web.pdf}}</ref> | |||
| The Dozenal Society of Great Britain (DSGB) proposed symbols {{angbr|1={{NNBSP}}<span style="display: inline-block; transform: scale(-1);">{{math|2}}</span>, <span style="display: inline-block; transform: scale(-1);">{{math|3}}</span>{{NNBSP}}}}.<ref name="Symbology Overview"/> This notation, derived from Arabic digits by 180° rotation, was introduced by ] in 1857.<ref name="Symbology Overview"/><ref name="Pitman1857">{{cite news |last=Pitman |first=Isaac |author-link=Isaac Pitman |title=A Reckoning Reform |newspaper=Bedfordshire Independent |date=24 November 1857 }} Reprinted as {{cite journal |last=Pitman |first=Isaac |display-authors=0 |title=Sir Isaac Pitman on the Dozen System: A Reckoning Reform |journal=The Duodecimal Bulletin |volume=3 |issue=2 |pages=1–5 |year=1947 |url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue032-web_0.pdf }}</ref> In March 2013, a proposal was submitted to include the digit forms for ten and eleven propagated by the Dozenal Societies in the ].<ref name="N4399">{{cite web |author=Pentzlin |first=Karl |date=March 30, 2013 |title=Proposal to encode Duodecimal Digit Forms in the UCS |url=https://www.unicode.org/wg2/docs/n4399.pdf |publisher=ISO/IEC JTC1/SC2/WG2 |access-date=2024-06-25}}</ref> Of these, the British/Pitman forms were accepted for encoding as characters at code points {{unichar|218A|TURNED DIGIT TWO}} and {{unichar|218B|TURNED DIGIT THREE}}. They were included in ] (2015).<ref name="Unicode8">{{cite web|url=https://www.unicode.org/charts/PDF/Unicode-8.0/U80-2150.pdf|title=The Unicode Standard, Version 8.0: Number Forms|publisher=Unicode Consortium|access-date=2016-05-30}}</ref><ref>{{cite web | |||
| | url = https://www.unicode.org/charts/PDF/U2150.pdf | |||
| | title = The Unicode Standard 8.0 | |||
| | access-date = 2014-07-18 | |||
| }}</ref> | |||
| After the Pitman digits were added to Unicode, the DSA took a vote and then began publishing PDF content using the Pitman digits instead, but continues to use the letters X and E on its webpage.<ref>{{Cite web |last=The Dozenal Society of America |date=n.d. |title=What should the DSA do about transdecimal characters? |url=https://dozenal.org/drupal/content/what-should-dsa-do-about-transdecimal-characters.html |access-date=January 1, 2018 |website=Dozenal Society of America |publisher=The Dozenal Society of America}}</ref> | |||
| {| class="wikitable" id="transdecimal-symbols-table" style="font-size:90%; max-width:50em;" | |||
| ! colspan=2 | Symbols | |||
| ! style="width:20em" | Background | |||
| ! Note | |||
| |- | |||
| | <big>A</big> | |||
| | <big>B</big> | |||
| | As in ] | |||
| | Allows entry on typewriters. | |||
| |- | |||
| | <big>T</big> | |||
| | <big>E</big> | |||
| | Initials of ''Ten'' and ''Eleven'' | |||
| | Used (in lower case) in ]<ref>], ''The Cambridge Introduction to Serialism'' (New York: Cambridge University Press, 2008): 276. {{ISBN|978-0-521-68200-8}} (pbk).</ref> | |||
| |- | |||
| | <big>X</big> | |||
| | <big>E</big> | |||
| | X from the ]; <br> E from ''Eleven''. | |||
| | | | | ||
| |- | |||
| | <big>X</big> | |||
| | <big>Z</big> | |||
| | Origin of Z unknown | |||
| | Attributed to ] & ] by the DSA.<ref name="Symbology Overview" /> | |||
| |- | |||
| | <big>δ</big> | |||
| | <big>ε</big> | |||
| | Greek ] from {{lang|grc|δέκα}} "ten"; <br> ] from {{lang|grc|ένδεκα}} "eleven"<ref name="Symbology Overview"/> | |||
| | | |||
| |- | |||
| | <big>τ</big> | |||
| | <big>ε</big> | |||
| | Greek ], ]<ref name="Symbology Overview"/> | |||
| | | |||
| |- | |||
| | <big>W</big> | |||
| | <big>∂</big> | |||
| | W from doubling the Roman numeral V; <br> ∂ based on a pendulum | |||
| | Silvio Ferrari in ''Calcolo Decidozzinale'' (1854).<ref name="Ferrari 1854">{{cite book|first=Silvio |last=Ferrari|title=Calcolo Decidozzinale|date=1854|page=2}}</ref> | |||
| |- | |||
| | <big>''X''</big> | |||
| | <big>''Ɛ''</big> | |||
| | italic ''X'' pronounced "dec"; <br> rounded ] ''Ɛ'', pronounced "elf" | |||
| | Frank Andrews in ''New Numbers'' (1935), with italic ''0''–''9'' for other duodecimal numerals.<ref name="New Numbers 1935">{{cite book|first=Frank Emerson |last=Andrews |title=New Numbers: How Acceptance of a Duodecimal (12) Base Would Simplify Mathematics |date=1935 |page=52 |publisher=Harcourt, Brace and company |url=https://archive.org/details/newnumbershowacc0000fran/page/52/mode/1up?q=%22quantity+eleven%22 |url-access=limited}}</ref> | |||
| |- | |||
| | <big>{{mono|1=*}}</big> | |||
| | <big>{{mono|1=<nowiki>#</nowiki>}}</big> | |||
| | ] or six-pointed asterisk,<br/>] or octothorpe | |||
| | On ]s; used by Edna Kramer in ''The Main Stream of Mathematics'' (1951); used by the DSA {{nobr|1974–2008}}<ref name="bellchange">{{cite journal|title=Annual Meeting of 1973 and Meeting of the Board|journal=The Duodecimal Bulletin|volume=25 |issue=1|date=1974|url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue251-web_0.pdf}}</ref><ref name="classic">{{cite journal|last=De Vlieger|first=Michael|title=Going Classic|journal=The Duodecimal Bulletin|volume=49 |issue=2|date=2008|url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue492_0.pdf}}</ref><ref name="Symbology Overview"/> | |||
| |- | |||
| | <big><span style="display: inline-block; transform: scale(-1);">2</span></big> | |||
| | <big><span style="display: inline-block; transform: scale(-1);">3</span></big> | |||
| | {{ubli | |||
| | Digits 2 and 3 rotated 180° | |||
| }} | |||
| | ] (1857);<ref name="Pitman1857"/> used by the DSGB; used by the DSA since 2015; included in ] (2015)<ref name="Unicode8">{{cite web|url=https://www.unicode.org/charts/PDF/Unicode-8.0/U80-2150.pdf|title=The Unicode Standard, Version 8.0: Number Forms|publisher=Unicode Consortium|access-date=2016-05-30}}</ref><ref>{{cite web | |||
| | url = https://www.unicode.org/charts/PDF/U2150.pdf | |||
| | title = The Unicode Standard 8.0 | |||
| | access-date = 2014-07-18 }}</ref> | |||
| |- | |||
| | <big>]</big> | |||
| | <big>]</big> | |||
| | Pronounced "dek", "el" | |||
| | {{ubl | |||
| |] (1945/1932?).<ref name="Symbology Overview"/><ref name="DB01">{{cite journal|title=Mo for Megro|journal=The Duodecimal Bulletin|volume=1|issue=1|date=1945|url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue011-web.pdf}}</ref> | |||
| |Used by the DSA 1945–1974 and 2008–2015<ref name="bellchange"/><ref name="classic" />}} | |||
| |} | |} | ||
| ==={{anchor|Humphrey point}}Base notation=== | |||
| The importance of 12 has been attributed to the number of lunar cycles in a year, and also to the fact that humans have 12 finger bones (]) on one hand (three on each of four fingers).<ref>{{Cite web | |||
| There are also varying proposals of how to distinguish a duodecimal number from a decimal one. The most common method used in mainstream mathematics sources comparing various number bases uses a subscript "10" or "12", e.g. "54<sub>12</sub> = 64<sub>10</sub>". To avoid ambiguity about the meaning of the subscript 10, the subscripts might be spelled out, "54<sub>twelve</sub> = 64<sub>ten</sub>". In 2015 the Dozenal Society of America adopted the more compact single-letter abbreviation "z" for "do'''z'''enal" and "d" for "'''d'''ecimal", "54<sub>z</sub> = 64<sub>d</sub>".<ref name="Volan 2015">{{Cite journal |last=Volan |first=John |date=July 2015 |title=Base Annotation Schemes |url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue521.pdf |journal=The Duodecimal Bulletin |volume=62}}</ref> | |||
| | title=ヒマラヤの満月と十二進法 (The Full Moon in the Himalayas and the Duodecimal System) | |||
| | last=Nishikawa | |||
| | first=Yoshiaki | |||
| | year=2002 | |||
| | url=http://www.kankyok.co.jp/nue/nue11/nue11_01.html | |||
| | accessdate=2008-03-24 | |||
| | postscript=<!-- Bot inserted parameter. Either remove it; or change its value to "." for the cite to end in a ".", as necessary. -->{{inconsistent citations}} | |||
| }}{{dead link|date=January 2014}}</ref> It is possible to count to 12 with the thumb acting as a pointer, touching each finger bone in turn. A traditional ] system still in use in many regions of Asia works in this way, and could help to explain the occurrence of numeral systems based on 12 and 60 besides those based on 10, 20 and 5. In this system, the one (usually right) hand counts repeatedly to 12, displaying the number of iterations on the other (usually left), until five dozens, i. e. the 60, are full.<ref name=Ifrah>{{Cite book | |||
| | last = Ifrah | |||
| | first = Georges | |||
| | author-link = Georges Ifrah | |||
| | title = The Universal History of Numbers: From prehistory to the invention of the computer | |||
| | publisher = ] | |||
| | year= 2000 | |||
| | page = | |||
| | isbn = 0-471-39340-1 | |||
| | postscript = <!-- Bot inserted parameter. Either remove it; or change its value to "." for the cite to end in a ".", as necessary. -->{{inconsistent citations}} | |||
| }}. Translated from the French by David Bellos, E.F. Harding, Sophie Wood and Ian Monk.</ref><ref name=Macey>{{Cite book|last=Macey|first=Samuel L.|title=The Dynamics of Progress: Time, Method, and Measure|year=1989|publisher=University of Georgia Press|location=Atlanta, Georgia|isbn=978-0-8203-3796-8|page=92|url=http://books.google.com/books?id=xlzCWmXguwsC&pg=PA92&lpg=PA92|postscript=<!-- Bot inserted parameter. Either remove it; or change its value to "." for the cite to end in a ".", as necessary. -->{{inconsistent citations}}}}</ref> | |||
| Other proposed methods include italicizing duodecimal numbers "''54'' = 64", adding a "Humphrey point" (a ] instead of a ]) to duodecimal numbers "54;6 = 64.5", prefixing duodecimal numbers by an asterisk "*54 = 64", or some combination of these. The Dozenal Society of Great Britain uses an asterisk prefix for duodecimal whole numbers, and a Humphrey point for other duodecimal numbers.<ref name="Volan 2015" /> | |||
| == Places == | |||
| In a duodecimal place system, ] can be written as <span style="display:inline-block;top:0.5em;transform:matrix(-1, 0, 0, -1, 0, 0);-moz-transform: matrix(-1, 0, 0, -1, 0, 0);-webkit-transform: matrix(-1, 0, 0, -1, 0, 0);-o-transform:matrix(-1, 0, 0, -1, 0, 0);">2</span>, ᘔ, or {{unicode|↊}} (a rotated digit two); ] can be written as <span style="display:inline-block;top:0.5em;transform:matrix(-1, 0, 0, 1, 0, 0);-moz-transform: matrix(-1, 0, 0, 1, 0, 0);-webkit-transform: matrix(-1, 0, 0, 1, 0, 0);-o-transform:matrix(-1, 0, 0, 1, 0, 0);">3</span>, Ɛ, or {{unicode|↋}} (a reversed digit three); and twelve is written as 10. For alternative symbols, see ]. | |||
| === Pronunciation === | |||
| According to this notation, duodecimal 50 expresses the same quantity as decimal ] (= five times twelve), duodecimal 60 is equivalent to decimal ] (= six times twelve = half a gross), duodecimal 100 has the same value as decimal ] (= twelve times twelve = one gross), etc. | |||
| The Dozenal Society of America suggested the pronunciation of ten and eleven as "dek" and "el". For the names of powers of twelve, there are two prominent systems. In spite of the efficiency of these newer systems, terms for powers of twelve either already exist or remain easily reconstructed in English using words and affixes. | |||
| ==== Base-12 nomenclature in English ==== | |||
| == Comparison to other numeral systems == | |||
| {{Unreferenced section|date=November 2024}} | |||
| ] | |||
| Another nominal for ] (12<sub>]</sub>) is a '']'' (10<sub>12</sub> ''or'' 1•10<sup>1</sup><sub>12</sub>). | |||
| The number 12 has six factors, which are ], ], ], ], ], and ], of which 2 and 3 are ]. The decimal system has only four factors, which are ], ], ], and ]; of which 2 and 5 are prime. ] adds two factors to those of ten, namely ] and ], but no additional prime factor. Although twenty has 6 factors, 2 of them prime, similarly to twelve, it is also a much larger base (i.e. the digit set and the multiplication table are much larger). Binary has only two factors, 1 and 2, the latter being prime. Hexadecimal has five factors, adding 4, ] and ] to those of 2, but no additional prime. Trigesimal is the smallest system that has three different prime factors (all of the three smallest primes: 2, 3 and 5) and it has eight factors in total (1, 2, 3, 5, 6, 10, 15, and 30). ]—which the ancient ] and ]ns among others actually used—adds the four convenient factors 4, 12, 20, and 60 to this but no new prime factors. The smallest system that has four different prime factors is base 210 and the pattern follows the ]s. In all base systems, there are similarities to the representation of multiples of numbers which are one less than the base.{{Clear}}<!-- the {{-}} template keeps the multiplication table from squeezing the heading for the next section--> | |||
| ] (144<sub>10</sub>) is also known as a ] (100<sub>12</sub> ''or'' 1•10<sup>2</sup><sub>12</sub>). | |||
| ] is (1728<sub>10</sub>) also known as a ''great-gross'' (1,000<sub>12</sub> or 1•10<sup>3</sup><sub>12</sub>). | |||
| For the next ] of twelve that follow those aforementioned, the affixes (dozen-, gross-, great-) are used to produce names for these powers of twelve that have a greater ] value. ]<sub>10</sub> or 10,000<sub>12</sub> may be rendered a ''dozen-great-gross''; so ]<sub>10</sub> or 100,000<sub>12</sub> is a ''gross-great-gross'', with ]<sub>10</sub> or 1,000,000<sub>12</sub> being known as a ''great-great-gross''. | |||
| It should be made plain that the indice's being a multiple of three, e.g. 10<sup>3</sup><sub>12</sub> , 10<sup>6</sup><sub>12</sub> , 10<sup>9</sup><sub>12</sub> results, in these examples, in a ''great gross'', a ''great-great-gross'', and a ''great-great-great-gross'', respectively. | |||
| {| class="wikitable" | |||
| ! Scientific notation||Positional notation||Name||Decimal | |||
| |- | |||
| |style="text-align:center"|1•10<sup>0</sup> | |||
| |1 | |||
| |style="text-align:center"|One | |||
| |1 | |||
| |- | |||
| |style="text-align:center" |A•10<sup>0</sup> | |||
| |A | |||
| |Ten | |||
| |10 | |||
| |- | |||
| |style="text-align:center" |B•10<sup>0</sup> | |||
| |B | |||
| |Eleven | |||
| |11 | |||
| |- | |||
| | style="text-align:center" |1•10<sup>1</sup> | |||
| |10 | |||
| | style="text-align:center" |Twelve | |||
| |12 | |||
| |- | |||
| | style="text-align:center" |5•10<sup>1</sup> | |||
| |50 | |||
| | style="text-align:center" |Five dozen | |||
| |60 | |||
| |- | |||
| | style="text-align:center" |1•10<sup>2</sup> | |||
| |100 | |||
| | style="text-align:center" |One gross | |||
| |144 | |||
| |- | |||
| | style="text-align:center" |2;6•10<sup>2</sup> | |||
| |260 | |||
| | style="text-align:center" |Two gross, six dozen | |||
| |360 | |||
| |- | |||
| | style="text-align:center" |1•10<sup>3</sup> | |||
| |1,000 | |||
| | style="text-align:center" |One great-gross | |||
| |1,728 | |||
| |- | |||
| | style="text-align:center" |1•10<sup>4</sup> | |||
| |10,000 | |||
| | style="text-align:center" |One dozen-great-gross | |||
| |20,736 | |||
| |- | |||
| | style="text-align:center" |1•10<sup>5</sup> | |||
| |100,000 | |||
| | style="text-align:center" |One gross-great-gross | |||
| |248,832 | |||
| |- | |||
| | style="text-align:center" |1•10<sup>6</sup> | |||
| |1,000,000 | |||
| | style="text-align:center" |One great-great-gross | |||
| |2,985,984 | |||
| |} | |||
| ==== Duodecimal numbers ==== | |||
| In this system, the prefix ''e''- is added for fractions.<ref name="DB01"/><ref name="Zirkel2010">{{cite journal|last=Zirkel|first=Gene|title=How Do You Pronounce Dozenals? | |||
| |journal=The Duodecimal Bulletin|volume=4E |issue=2|date=2010|url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue4b2_0.pdf }}</ref> | |||
| {| class="wikitable" | |||
| ! Duodecimal <br> number||Number <br> name||Decimal <br> number||Duodecimal <br> fraction||Fraction <br> name | |||
| |- | |||
| |style="text-align:right"|1; | |||
| |one | |||
| |style="text-align:right"|1 | |||
| |colspan="2"| | |||
| |- | |||
| | style="text-align:right" |10; | |||
| |{{abbr|do|pronounced 'doʊ'}} | |||
| |style="text-align:right"|12 | |||
| |0;1||edo | |||
| |- | |||
| | style="text-align:right" |100; | |||
| |{{abbr|gro|pronounced 'ɡroʊ'}} | |||
| |style="text-align:right"|144 | |||
| |0;01 | |||
| |egro | |||
| |- | |||
| | style="text-align:right" |1,000; | |||
| |{{abbr|mo|pronounced 'moʊ'}} | |||
| |style="text-align:right"|1,728 | |||
| |0;001 | |||
| |emo | |||
| |- | |||
| | style="text-align:right" |10,000; | |||
| |do-mo | |||
| |style="text-align:right"|20,736 | |||
| |0;000,1 | |||
| |edo-mo | |||
| |- | |||
| | style="text-align:right" |100,000; | |||
| |gro-mo | |||
| |style="text-align:right"|248,832 | |||
| |0;000,01 | |||
| |egro-mo | |||
| |- | |||
| | style="text-align:right" |1,000,000; | |||
| |bi-mo | |||
| |style="text-align:right" |2,985,984 | |||
| |0;000,001 | |||
| |ebi-mo | |||
| |- | |||
| | style="text-align:right" |10,000,000; | |||
| |do-bi-mo | |||
| |style="text-align:right"|35,831,808 | |||
| |0;000,000,1 | |||
| |edo-bi-mo | |||
| |- | |||
| | style="text-align:right" |100,000,000; | |||
| |gro-bi-mo | |||
| |style="text-align:right"|429,981,696 | |||
| |0;000,000,01 | |||
| |egro-bi-mo | |||
| |} | |||
| As numbers get larger (or fractions smaller), the last two morphemes are successively replaced with tri-mo, quad-mo, penta-mo, and so on. | |||
| Multiple digits in this series are pronounced differently: 12 is "do two"; 30 is "three do"; 100 is "gro"; {{d3}}{{d2}}9 is "el gro dek do nine"; {{d3}}86 is "el gro eight do six"; 8{{d3}}{{d3}},15{{d2}} is "eight gro el do el, one gro five do dek"; ABA is "dek gro el do dek"; BBB is "el gro el do el"; 0.06 is "six egro"; and so on.<ref name="Zirkel2010"/> | |||
| ==== Systematic Dozenal Nomenclature (SDN) ==== | |||
| This system uses "-qua" ending for the positive powers of 12 and "-cia" ending for the negative powers of 12, and an extension of the IUPAC ]s (with syllables '''dec''' and '''lev''' for the two extra digits needed for duodecimal) to express which power is meant.<ref name="DBX1">{{cite journal |url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue511a_0.pdf |title=Systematic Dozenal Nomenclature and other nomenclature system. |journal=The Duodecimal Bulletin |volume=61 |number=1 }}</ref><ref name="DSAGoodman2016"/> | |||
| {| class="wikitable" | |||
| ! Duodecimal <br> number||Number <br> name||Decimal <br> number||Duodecimal <br> fraction||Fraction <br> name | |||
| |- | |||
| |style="text-align:right"|1; | |||
| |one | |||
| |style="text-align:right"|1 | |||
| |colspan="2"| | |||
| |- | |||
| |style="text-align:right"|10; | |||
| |unqua | |||
| |style="text-align:right"|12 | |||
| |0;1 | |||
| |uncia | |||
| |- | |||
| |style="text-align:right"|100; | |||
| |biqua | |||
| |style="text-align:right"|144 | |||
| |0;01 | |||
| |bicia | |||
| |- | |||
| |style="text-align:right"|1,000; | |||
| |triqua | |||
| |style="text-align:right"|1,728 | |||
| |0;001 | |||
| |tricia | |||
| |- | |||
| |style="text-align:right"|10,000; | |||
| |quadqua | |||
| |style="text-align:right"|20,736 | |||
| |0;000,1 | |||
| |quadcia | |||
| |- | |||
| |style="text-align:right"|100,000; | |||
| |pentqua | |||
| |style="text-align:right"|248,832 | |||
| |0;000,01 | |||
| |pentcia | |||
| |- | |||
| |style="text-align:right"|1,000,000; | |||
| |hexqua | |||
| |style="text-align:right"|2,985,984 | |||
| |0;000,001 | |||
| |hexcia | |||
| |} | |||
| After hex-, further prefixes continue sept-, oct-, enn-, dec-, lev-, unnil-, unun-. | |||
| == Advocacy and "dozenalism" == | |||
| ] used 12 as the base for his constructed language ] in 1906, noting it being the smallest number with four factors and its prevalence in commerce.<ref>The Prodigy (Biography of WJS) pg </ref> | |||
| The case for the duodecimal system was put forth at length in ]' 1935 book ''New Numbers: How Acceptance of a Duodecimal Base Would Simplify Mathematics''. Emerson noted that, due to the prevalence of factors of twelve in many traditional units of weight and measure, many of the computational advantages claimed for the metric system could be realized ''either'' by the adoption of ten-based weights and measure ''or'' by the adoption of the duodecimal number system.<ref name="New Numbers 1935"/> | |||
| ]]] | |||
| Both the Dozenal Society of America and the Dozenal Society of Great Britain promote widespread adoption of the duodecimal system. They use the word "dozenal" instead of "duodecimal" to avoid the more overtly decimal terminology. However, the etymology of "dozenal" itself is also an expression based on decimal terminology since "dozen" is a direct derivation of the French word ''douzaine'', which is a derivative of the French word for twelve, '']'', descended from Latin ''duodecim''. | |||
| Mathematician and mental calculator ] was an outspoken advocate of duodecimal: | |||
| {{blockquote|text=The duodecimal tables are easy to master, easier than the decimal ones; and in elementary teaching they would be so much more interesting, since young children would find more fascinating things to do with twelve rods or blocks than with ten. Anyone having these tables at command will do these calculations more than one-and-a-half times as fast in the duodecimal scale as in the decimal. This is my experience; I am certain that even more so it would be the experience of others.|author=A. C. Aitken|source="Twelves and Tens" in ''The Listener'' (January 25, 1962)<ref>A. C. Aitken (January 25, 1962) ''The Listener''.</ref>}} | |||
| {{Blockquote|text=But the final quantitative advantage, in my own experience, is this: in varied and extensive calculations of an ordinary and not unduly complicated kind, carried out over many years, I come to the conclusion that the efficiency of the decimal system might be rated at about 65 or less, if we assign 100 to the duodecimal.|author=A. C. Aitken|source=''The Case Against Decimalisation'' (1962)<ref>A. C. Aitken (1962) . Edinburgh / London: Oliver & Boyd.</ref>}} | |||
| === In media === | |||
| In "Little Twelvetoes," an episode of the American educational television series '']'', a farmer encounters an alien being with twelve fingers on each hand and twelve toes on each foot who uses duodecimal arithmetic. The alien uses "dek" and "el" as names for ten and eleven, and Andrews' script-X and script-E for the digit symbols.<ref>{{cite web|url=http://www.schoolhouserock.tv/Little.html|archive-url=https://web.archive.org/web/20100206052053/http://www.schoolhouserock.tv/Little.html|url-status=dead|archive-date=6 February 2010|title=SchoolhouseRock - Little Twelvetoes|date=6 February 2010}}</ref><ref>{{Cite book|last=Bellos|first=Alex|url=https://books.google.com/books?id=FA_HwoEzSQUC|title=Alex's Adventures in Numberland|date=2011-04-04|publisher=A&C Black|isbn=978-1-4088-0959-4|pages=50|language=en|author-link=Alex Bellos}}</ref> | |||
| === Duodecimal systems of measurements === | |||
| ] proposed by dozenalists include: | |||
| * Tom Pendlebury's TGM system<ref>{{cite web|last1=Pendlebury|first1=Tom|last2=Goodman|first2=Donald|title=TGM: A Coherent Dozenal Metrology|url=http://www.dozenal.org/drupal/sites_bck/default/files/tgm_0.pdf |date=2012|publisher=The Dozenal Society of Great Britain}}</ref><ref name="DSAGoodman2016">{{cite web |last=Goodman |first=Donald |title=Manual of the Dozenal System |date=2016 |url=http://www.dozenal.org/drupal/sites_bck/default/files/DSA_mods_rev.pdf |publisher=Dozenal Society of America|access-date=27 April 2018}}</ref> | |||
| * Takashi Suga's Universal Unit System<ref>{{cite web|last=Suga|first=Takashi|title=Proposal for the Universal Unit System|url=http://www.asahi-net.or.jp/~dd6t-sg/univunit-e/revised.pdf |date=22 May 2019}}</ref><ref name="DSAGoodman2016" /> | |||
| * John Volan's Primel system<ref>{{cite journal |last1=Volan |first1=John |date= |title=The Primel Metrology |url=http://www.dozenal.org/drupal/sites_bck/default/files/DuodecimalBulletinIssue531.pdf |journal=The Duodecimal Bulletin |volume=63 |issue=1 |pages=38–60<!--be careful; the Duodecimal Bulletin, as one might expect, numbers its pages in duodecimal--> }}</ref> | |||
| == Comparison to other number systems == | |||
| :''In this section, numerals are in decimal. For example, "10" means 9+1, and "12" means 9+3.'' | |||
| The Dozenal Society of America argues that if a base is too small, significantly longer expansions are needed for numbers; if a base is too large, one must memorise a large multiplication table to perform arithmetic. Thus, it presumes that "a number base will need to be between about 7 or 8 through about 16, possibly including 18 and 20".<ref name="dsafaq" /> | |||
| The number 12 has six factors, which are ], ], ], ], ], and ], of which 2 and 3 are ]. It is the smallest number to have six factors, the largest number to have at least half of the numbers below it as divisors, and is only slightly larger than 10. (The numbers 18 and 20 also have six factors but are much larger.) Ten, in contrast, only has four factors, which are ], ], ], and ], of which 2 and 5 are prime.<ref name="dsafaq" /> Six shares the prime factors 2 and 3 with twelve; however, like ten, six only has four factors (1, 2, 3, and 6) instead of six. Its corresponding base, ], is below the DSA's stated threshold. | |||
| ] and ] only have 2 as a prime factor. Therefore, in ] and ], the only ] are those whose ] is a ]. | |||
| ] is the smallest number that has three different prime factors (2, 3, and 5, the first three primes), and it has eight factors in total (1, 2, 3, 5, 6, 10, 15, and 30). ] was actually used by the ancient ]ians and ]ns, among others; its base, ], adds the four convenient factors 4, 12, 20, and 60 to 30 but no new prime factors. The smallest number that has four different prime factors is ]; the pattern follows the ]s. However, these numbers are quite large to use as bases, and are far beyond the DSA's stated threshold. | |||
| In all base systems, there are similarities to the representation of multiples of numbers that are one less than or one more than the base.{{Clear}}''In the following multiplication table, numerals are written in duodecimal. For example, "10" means twelve, and "12" means fourteen.''<!-- the {{-}} template keeps the multiplication table from squeezing the heading for the next section--> | |||
| {| class="wikitable" style="text-align: right;" | |||
| |+ Duodecimal multiplication table | |||
| !style="width:7.69%"|× | |||
| !style="text-align: right; width:7.69%"|1 | |||
| !style="text-align: right; width:7.69%"|2 | |||
| !style="text-align: right; width:7.69%"|3 | |||
| !style="text-align: right; width:7.69%"|4 | |||
| !style="text-align: right; width:7.69%"|5 | |||
| !style="text-align: right; width:7.69%"|6 | |||
| !style="text-align: right; width:7.69%"|7 | |||
| !style="text-align: right; width:7.69%"|8 | |||
| !style="text-align: right; width:7.69%"|9 | |||
| !style="text-align: right; width:7.69%"|{{d2}} | |||
| !style="text-align: right; width:7.69%"|{{d3}} | |||
| !style="text-align: right; width:7.69%"|10 | |||
| |- | |||
| !style="text-align: right; width:7.69%"|1 | |||
| |1||2||3||4||5||6||7||8||9||{{d2}}||{{d3}}||10 | |||
| |- | |||
| !style="text-align: right;"|2 | |||
| |2||4||6||8||{{d2}}||10||12||14||16||18||1{{d2}}||20 | |||
| |- | |||
| !style="text-align: right;|3 | |||
| |3||6||9||10||13||16||19||20||23||26||29||30 | |||
| |- | |||
| !style="text-align: right;"|4 | |||
| |4||8||10||14||18||20||24||28||30||34||38||40 | |||
| |- | |||
| !style="text-align: right;"|5 | |||
| |5||{{d2}}||13||18||21||26||2{{d3}}||34||39||42||47||50 | |||
| |- | |||
| !style="text-align: right;"|6 | |||
| |6||10||16||20||26||30||36||40||46||50||56||60 | |||
| |- | |||
| !style="text-align: right;"|7 | |||
| |7||12||19||24||2{{d3}}||36||41||48||53||5{{d2}}||65||70 | |||
| |- | |||
| !style="text-align: right;"|8 | |||
| |8||14||20||28||34||40||48||54||60||68||74||80 | |||
| |- | |||
| !style="text-align: right;"|9 | |||
| |9||16||23||30||39||46||53||60||69||76||83||90 | |||
| |- | |||
| !style="text-align: right;"|{{d2}} | |||
| |{{d2}}||18||26||34||42||50||5{{d2}}||68||76||84||92||A0 | |||
| |- | |||
| !style="text-align: right;"|{{d3}} | |||
| |{{d3}}||1{{d2}}||29||38||47||56||65||74||83||92||{{d2}}1||B0 | |||
| |- | |||
| !style="text-align: right;"|10 | |||
| |10||20||30||40||50||60||70||80||90||A0||B0||100 | |||
| |} | |||
| == Conversion tables to and from decimal == | == Conversion tables to and from decimal == | ||
| To convert numbers between bases, one can use the general conversion algorithm (see the relevant section under ]). Alternatively, one can use digit-conversion tables. The ones provided below can be used to convert any duodecimal number between 0 |
To convert numbers between bases, one can use the general conversion algorithm (see the relevant section under ]). Alternatively, one can use digit-conversion tables. The ones provided below can be used to convert any duodecimal number between 0;1 and {{d3}}{{d3}},{{d3}}{{d3}}{{d3}};{{d3}} to decimal, or any decimal number between 0.1 and 99,999.9 to duodecimal. To use them, the given number must first be decomposed into a sum of numbers with only one significant digit each. For example: | ||
| :12,345.6 = 10,000 + 2,000 + 300 + 40 + 5 + 0.6 | |||
| This decomposition works the same no matter what base the number is expressed in. Just isolate each non-zero digit, padding them with as many zeros as necessary to preserve their respective place values. If the digits in the given number include zeroes (for example, |
This decomposition works the same no matter what base the number is expressed in. Just isolate each non-zero digit, padding them with as many zeros as necessary to preserve their respective place values. If the digits in the given number include zeroes (for example, 7,080.9), these are left out in the digit decomposition (7,080.9 = 7,000 + 80 + 0.9). Then, the digit conversion tables can be used to obtain the equivalent value in the target base for each digit. If the given number is in duodecimal and the target base is decimal, we get: | ||
| <small>(duodecimal)</small> |
:<small>(duodecimal)</small> 10,000 + 2,000 + 300 + 40 + 5 + 0;6 <br> = <small>(decimal)</small> 20,736 + 3,456 + 432 + 48 + 5 + 0.5 | ||
| Because the summands are already converted to decimal, the usual decimal arithmetic is used to perform the addition and recompose the number, arriving at the conversion result: | |||
| Duodecimal |
Duodecimal ---> Decimal | ||
| |
10,000 = 20,736 | ||
| |
2,000 = 3,456 | ||
| |
300 = 432 | ||
| |
40 = 48 | ||
| |
5 = 5 | ||
| + |
+ 0;6 = + 0.5 | ||
| ----------------------------- | |||
| 0.7 = 0.58{{overline|3}}333333333... | |||
| 12,345;6 = 24,677.5 | |||
| 0.08 = 0.0{{overline|5}}5555555555... | |||
| -------------------------------------------- | |||
| 123,456.78 = 296,130.63{{overline|8}}888888888... | |||
| That is, <small>(duodecimal)</small> |
That is, <small>(duodecimal)</small> 12,345;6 equals <small>(decimal)</small> 24,677.5 | ||
| If the given number is in decimal and the target base is duodecimal, the method is |
If the given number is in decimal and the target base is duodecimal, the method is same. Using the digit conversion tables: | ||
| <small>(decimal)</small> |
<small>(decimal)</small> 10,000 + 2,000 + 300 + 40 + 5 + 0.6 <br> = <small>(duodecimal)</small> 5,954 + 1,1{{d2}}8 + 210 + 34 + 5 + 0;{{overline|7249}} | ||
| To sum these partial products and recompose the number, the addition must be done with duodecimal rather than decimal arithmetic: | |||
| However, in order to do this sum and recompose the number, now the addition tables for the duodecimal system have to be used, instead of the addition tables for decimal most people are already familiar with, because the summands are now in base twelve and so the arithmetic with them has to be in duodecimal as well. In decimal, 6 + 6 equals 12, but in duodecimal it equals 10; so, if using decimal arithmetic with duodecimal numbers one would arrive at an incorrect result. Doing the arithmetic properly in duodecimal, one gets the result: | |||
| Decimal |
Decimal --> Duodecimal | ||
| |
10,000 = 5,954 | ||
| |
2,000 = 1,1{{d2}}8 | ||
| |
300 = 210 | ||
| |
40 = 34 | ||
| |
5 = 5 | ||
| + |
+ 0.6 = + 0;{{overline|7249}} | ||
| ------------------------------- | |||
| 0.7 = 0.8{{overline|4972}}4972497249724972497... | |||
| |
12,345.6 = 7,189;{{overline|7249}} | ||
| -------------------------------------------------------- | |||
| 123,456.78 = 5Ɛ,540.9{{overline|43ᘔ0Ɛ62ᘔ68781Ɛ059153}}43ᘔ... | |||
| That is, <small>(decimal)</small> |
That is, <small>(decimal)</small> 12,345.6 equals <small>(duodecimal)</small> 7,189;{{overline|7249}} | ||
| === Duodecimal to decimal digit conversion === | === Duodecimal to decimal digit conversion === | ||
| {|class="wikitable" | {| class="wikitable" | ||
| ! Duod. | |||
| |- | |||
| ! Dec. | |||
| | style="background:silver;"| '''''Duod.''''' | |||
| ! Duod. | |||
| | ''Dec.'' | |||
| ! Dec. | |||
| | style="background:silver;"| '''''Duod.''''' | |||
| ! Duod. | |||
| | ''Dec.'' | |||
| ! Dec. | |||
| | style="background:silver;"| '''''Duod.''''' | |||
| ! Duod. | |||
| | ''Dec.'' | |||
| ! Dec. | |||
| | style="background:silver;"| '''''Duod.''''' | |||
| ! Duod. | |||
| | ''Dec.'' | |||
| ! Dec. | |||
| | style="background:silver;"| '''''Duod.''''' | |||
| ! Duod. | |||
| | ''Dec.'' | |||
| ! Dec. | |||
| | style="background:silver;"| '''''Duod.''''' | |||
| |- style="text-align:right" | |||
| | ''Dec.'' | |||
| | style="background:silver;"| '''''Duod.''''' | |||
| | ''Dec.'' | |||
| | style="background:silver;"| '''''Duod.''''' | |||
| | ''Dec.'' | |||
| |- | |||
| | style="background:silver;"| '''100,000''' | |||
| | 248,832 | |||
| | style="background:silver;"| '''10,000''' | | style="background:silver;"| '''10,000''' | ||
| | 20,736 | | 20,736 | ||
| Line 198: | Line 525: | ||
| | style="background:silver;"| '''1''' | | style="background:silver;"| '''1''' | ||
| | 1 | | 1 | ||
| | style="background:silver;"| '''0 |
| style="background:silver;"| '''0;1''' | ||
| | 0.08{{overline|3}} | | style="text-align:left" | 0.08{{overline|3}} | ||
| | style=" |
|- style="text-align:right" | ||
| | 0.0069{{overline|4}} | |||
| |- | |||
| | style="background:silver;"| '''200,000''' | |||
| | 497,664 | |||
| | style="background:silver;"| '''20,000''' | | style="background:silver;"| '''20,000''' | ||
| | 41,472 | | 41,472 | ||
| Line 215: | Line 538: | ||
| | style="background:silver;"| '''2''' | | style="background:silver;"| '''2''' | ||
| | 2 | | 2 | ||
| | style="background:silver;"| '''0 |
| style="background:silver;"| '''0;2''' | ||
| | 0.1{{overline|6}} | | style="text-align:left" | 0.1{{overline|6}} | ||
| | style=" |
|- style="text-align:right" | ||
| | 0.013{{overline|8}} | |||
| |- | |||
| | style="background:silver;"| '''300,000''' | |||
| | 746,496 | |||
| | style="background:silver;"| '''30,000''' | | style="background:silver;"| '''30,000''' | ||
| | 62,208 | | 62,208 | ||
| Line 232: | Line 551: | ||
| | style="background:silver;"| '''3''' | | style="background:silver;"| '''3''' | ||
| | 3 | | 3 | ||
| | style="background:silver;"| '''0 |
| style="background:silver;"| '''0;3''' | ||
| | style="text-align:left" | 0.25 | |||
| | 0.25 | |||
| | style=" |
|- style="text-align:right" | ||
| | 0.0208{{overline|3}} | |||
| |- | |||
| | style="background:silver;"| '''400,000''' | |||
| | 995,328 | |||
| | style="background:silver;"| '''40,000''' | | style="background:silver;"| '''40,000''' | ||
| | 82,944 | | 82,944 | ||
| Line 249: | Line 564: | ||
| | style="background:silver;"| '''4''' | | style="background:silver;"| '''4''' | ||
| | 4 | | 4 | ||
| | style="background:silver;"| '''0 |
| style="background:silver;"| '''0;4''' | ||
| | 0.{{overline|3}} | | style="text-align:left" | 0.{{overline|3}} | ||
| | style=" |
|- style="text-align:right" | ||
| | 0.02{{overline|7}} | |||
| |- | |||
| | style="background:silver;"| '''500,000''' | |||
| | 1,244,160 | |||
| | style="background:silver;"| '''50,000''' | | style="background:silver;"| '''50,000''' | ||
| | 103,680 | | 103,680 | ||
| Line 266: | Line 577: | ||
| | style="background:silver;"| '''5''' | | style="background:silver;"| '''5''' | ||
| | 5 | | 5 | ||
| | style="background:silver;"| '''0 |
| style="background:silver;"| '''0;5''' | ||
| | 0.41{{overline|6}} | | style="text-align:left" | 0.41{{overline|6}} | ||
| | style=" |
|- style="text-align:right" | ||
| | 0.0347{{overline|2}} | |||
| |- | |||
| | style="background:silver;"| '''600,000''' | |||
| | 1,492,992 | |||
| | style="background:silver;"| '''60,000''' | | style="background:silver;"| '''60,000''' | ||
| | 124,416 | | 124,416 | ||
| Line 283: | Line 590: | ||
| | style="background:silver;"| '''6''' | | style="background:silver;"| '''6''' | ||
| | 6 | | 6 | ||
| | style="background:silver;"| '''0 |
| style="background:silver;"| '''0;6''' | ||
| | style="text-align:left" | 0.5 | |||
| | 0.5 | |||
| | style=" |
|- style="text-align:right" | ||
| | 0.041{{overline|6}} | |||
| |- | |||
| | style="background:silver;"| '''700,000''' | |||
| | 1,741,824 | |||
| | style="background:silver;"| '''70,000''' | | style="background:silver;"| '''70,000''' | ||
| | 145,152 | | 145,152 | ||
| Line 295: | Line 598: | ||
| | 12,096 | | 12,096 | ||
| | style="background:silver;"| '''700''' | | style="background:silver;"| '''700''' | ||
| | |
| 1,008 | ||
| | style="background:silver;"| '''70''' | | style="background:silver;"| '''70''' | ||
| | 84 | | 84 | ||
| | style="background:silver;"| '''7''' | | style="background:silver;"| '''7''' | ||
| | 7 | | 7 | ||
| | style="background:silver;"| '''0 |
| style="background:silver;"| '''0;7''' | ||
| | 0.58{{overline|3}} | | style="text-align:left" | 0.58{{overline|3}} | ||
| | style=" |
|- style="text-align:right" | ||
| | 0.0486{{overline|1}} | |||
| |- | |||
| | style="background:silver;"| '''800,000''' | |||
| | 1,990,656 | |||
| | style="background:silver;"| '''80,000''' | | style="background:silver;"| '''80,000''' | ||
| | 165,888 | | 165,888 | ||
| Line 312: | Line 611: | ||
| | 13,824 | | 13,824 | ||
| | style="background:silver;"| '''800''' | | style="background:silver;"| '''800''' | ||
| | |
| 1,152 | ||
| | style="background:silver;"| '''80''' | | style="background:silver;"| '''80''' | ||
| | 96 | | 96 | ||
| | style="background:silver;"| '''8''' | | style="background:silver;"| '''8''' | ||
| | 8 | | 8 | ||
| | style="background:silver;"| '''0 |
| style="background:silver;"| '''0;8''' | ||
| | 0.{{overline|6}} | | style="text-align:left" | 0.{{overline|6}} | ||
| | style=" |
|- style="text-align:right" | ||
| | 0.0{{overline|5}} | |||
| |- | |||
| | style="background:silver;"| '''900,000''' | |||
| | 2,239,488 | |||
| | style="background:silver;"| '''90,000''' | | style="background:silver;"| '''90,000''' | ||
| | 186,624 | | 186,624 | ||
| Line 334: | Line 629: | ||
| | style="background:silver;"| '''9''' | | style="background:silver;"| '''9''' | ||
| | 9 | | 9 | ||
| | style="background:silver;"| '''0 |
| style="background:silver;"| '''0;9''' | ||
| | style="text-align:left" | 0.75 | |||
| | 0.75 | |||
| | style=" |
|- style="text-align:right" | ||
| | style="background:silver;"| '''{{nowrap|{{d2}}0,000}}''' | |||
| | 0.0625 | |||
| |- | |||
| | style="background:silver;"| '''ᘔ00,000''' | |||
| | 2,488,320 | |||
| | style="background:silver;"| '''ᘔ0,000''' | |||
| | 207,360 | | 207,360 | ||
| | style="background:silver;"| ''' |
| style="background:silver;"| '''{{d2}},000''' | ||
| | 17,280 | | 17,280 | ||
| | style="background:silver;"| ''' |
| style="background:silver;"| '''{{d2}}00''' | ||
| | 1,440 | | 1,440 | ||
| | style="background:silver;"| ''' |
| style="background:silver;"| '''{{d2}}0''' | ||
| | 120 | | 120 | ||
| | style="background:silver;"| ''' |
| style="background:silver;"| '''{{d2}}''' | ||
| | 10 | | 10 | ||
| | style="background:silver;"| '''0 |
| style="background:silver;"| '''0;{{d2}}''' | ||
| | 0.8{{overline|3}} | | style="text-align:left" | 0.8{{overline|3}} | ||
| | style=" |
|- style="text-align:right" | ||
| | style="background:silver;"| '''{{d3}}0,000''' | |||
| | 0.069{{overline|4}} | |||
| |- | |||
| | style="background:silver;"| '''Ɛ00,000''' | |||
| | 2,737,152 | |||
| | style="background:silver;"| '''Ɛ0,000''' | |||
| | 228,096 | | 228,096 | ||
| | style="background:silver;"| ''' |
| style="background:silver;"| '''{{d3}},000''' | ||
| | 19,008 | | 19,008 | ||
| | style="background:silver;"| ''' |
| style="background:silver;"| '''{{d3}}00''' | ||
| | 1,584 | | 1,584 | ||
| | style="background:silver;"| ''' |
| style="background:silver;"| '''{{d3}}0''' | ||
| | 132 | | 132 | ||
| | style="background:silver;"| ''' |
| style="background:silver;"| '''{{d3}}''' | ||
| | 11 | | 11 | ||
| | style="background:silver;"| '''0 |
| style="background:silver;"| '''0;{{d3}}''' | ||
| | 0.91{{overline|6}} | | style="text-align:left" | 0.91{{overline|6}} | ||
| | style="background:silver;"| '''0.0Ɛ''' | |||
| | 0.0763{{overline|8}} | |||
| |} | |} | ||
| === Decimal to duodecimal digit conversion === | === Decimal to duodecimal digit conversion === | ||
| {|class="wikitable" | {| class="wikitable" | ||
| ! Dec. | |||
| |- | |||
| ! Duod. | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| ! Dec. | |||
| | ''Duod.'' | |||
| ! Duod. | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| ! Dec. | |||
| | ''Duod.'' | |||
| ! Duod. | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| ! Dec. | |||
| | ''Duod.'' | |||
| ! Duod. | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| ! Dec. | |||
| | ''Duod.'' | |||
| ! Duod. | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| ! Dec. | |||
| | ''Duod.'' | |||
| ! Duodecimal | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| |- | |- | ||
| | style="background:silver;"| '''100,000''' | |||
| | 49,ᘔ54 | |||
| | style="background:silver;"| '''10,000''' | | style="background:silver;"| '''10,000''' | ||
| | 5,954 | | 5,954 | ||
| | style="background:silver;"| '''1,000''' | | style="background:silver;"| '''1,000''' | ||
| | 6{{d3}}4 | |||
| | 6Ɛ4 | |||
| | style="background:silver;"| '''100''' | | style="background:silver;"| '''100''' | ||
| | 84 | | 84 | ||
| | style="background:silver;"| '''10''' | | style="background:silver;"| '''10''' | ||
| | |
| {{d2}} | ||
| | style="background:silver;"| '''1''' | | style="background:silver;"| '''1''' | ||
| | 1 | | 1 | ||
| | style="background:silver;"| '''0.1''' | | style="background:silver;"| '''0.1''' | ||
| | 0 |
| 0;1{{overline|2497}} | ||
| | style="background:silver;"| '''0.01''' | |||
| | 0.0{{overline|15343ᘔ0Ɛ62ᘔ68781Ɛ059}} | |||
| |- | |- | ||
| | style="background:silver;"| '''200,000''' | |||
| | 97,8ᘔ8 | |||
| | style="background:silver;"| '''20,000''' | | style="background:silver;"| '''20,000''' | ||
| | {{d3}},6{{d2}}8 | |||
| | Ɛ,6ᘔ8 | |||
| | style="background:silver;"| '''2,000''' | | style="background:silver;"| '''2,000''' | ||
| | 1, |
| 1,1{{d2}}8 | ||
| | style="background:silver;"| '''200''' | | style="background:silver;"| '''200''' | ||
| | 148 | | 148 | ||
| Line 424: | Line 698: | ||
| | 2 | | 2 | ||
| | style="background:silver;"| '''0.2''' | | style="background:silver;"| '''0.2''' | ||
| | 0 |
| 0;{{overline|2497}} | ||
| | style="background:silver;"| '''0.02''' | |||
| | 0.0{{overline|2ᘔ68781Ɛ05915343ᘔ0Ɛ6}} | |||
| |- | |- | ||
| | style="background:silver;"| '''300,000''' | |||
| | 125,740 | |||
| | style="background:silver;"| '''30,000''' | | style="background:silver;"| '''30,000''' | ||
| | 15,440 | | 15,440 | ||
| | style="background:silver;"| '''3,000''' | | style="background:silver;"| '''3,000''' | ||
| | 1, |
| 1,8{{d2}}0 | ||
| | style="background:silver;"| '''300''' | | style="background:silver;"| '''300''' | ||
| | 210 | | 210 | ||
| Line 441: | Line 711: | ||
| | 3 | | 3 | ||
| | style="background:silver;"| '''0.3''' | | style="background:silver;"| '''0.3''' | ||
| | 0 |
| 0;3{{overline|7249}} | ||
| | style="background:silver;"| '''0.03''' | |||
| | 0.0{{overline|43ᘔ0Ɛ62ᘔ68781Ɛ059153}} | |||
| |- | |- | ||
| | style="background:silver;"| '''400,000''' | |||
| | 173,594 | |||
| | style="background:silver;"| '''40,000''' | | style="background:silver;"| '''40,000''' | ||
| | |
| 1{{d3}},194 | ||
| | style="background:silver;"| '''4,000''' | | style="background:silver;"| '''4,000''' | ||
| | 2,394 | | 2,394 | ||
| Line 458: | Line 724: | ||
| | 4 | | 4 | ||
| | style="background:silver;"| '''0.4''' | | style="background:silver;"| '''0.4''' | ||
| | 0 |
| 0;{{overline|4972}} | ||
| | style="background:silver;"| '''0.04''' | |||
| | 0.{{overline|05915343ᘔ0Ɛ62ᘔ68781Ɛ}} | |||
| |- | |- | ||
| | style="background:silver;"| '''500,000''' | |||
| | 201,428 | |||
| | style="background:silver;"| '''50,000''' | | style="background:silver;"| '''50,000''' | ||
| | 24, |
| 24,{{d3}}28 | ||
| | style="background:silver;"| '''5,000''' | | style="background:silver;"| '''5,000''' | ||
| | 2, |
| 2,{{d2}}88 | ||
| | style="background:silver;"| '''500''' | | style="background:silver;"| '''500''' | ||
| | 358 | | 358 | ||
| Line 475: | Line 737: | ||
| | 5 | | 5 | ||
| | style="background:silver;"| '''0.5''' | | style="background:silver;"| '''0.5''' | ||
| | 0 |
| 0;6 | ||
| | style="background:silver;"| '''0.05''' | |||
| | 0.0{{overline|7249}} | |||
| |- | |- | ||
| | style="background:silver;"| '''600,000''' | |||
| | 24Ɛ,280 | |||
| | style="background:silver;"| '''60,000''' | | style="background:silver;"| '''60,000''' | ||
| | |
| 2{{d2}},880 | ||
| | style="background:silver;"| '''6,000''' | | style="background:silver;"| '''6,000''' | ||
| | 3,580 | | 3,580 | ||
| Line 492: | Line 750: | ||
| | 6 | | 6 | ||
| | style="background:silver;"| '''0.6''' | | style="background:silver;"| '''0.6''' | ||
| | 0 |
| 0;{{overline|7249}} | ||
| | style="background:silver;"| '''0.06''' | |||
| | 0.0{{overline|8781Ɛ05915343ᘔ0Ɛ62ᘔ6}} | |||
| |- | |- | ||
| | style="background:silver;"| '''700,000''' | |||
| | 299,114 | |||
| | style="background:silver;"| '''70,000''' | | style="background:silver;"| '''70,000''' | ||
| | 34,614 | | 34,614 | ||
| Line 503: | Line 757: | ||
| | 4,074 | | 4,074 | ||
| | style="background:silver;"| '''700''' | | style="background:silver;"| '''700''' | ||
| | 4{{d2}}4 | |||
| | 4ᘔ4 | |||
| | style="background:silver;"| '''70''' | | style="background:silver;"| '''70''' | ||
| | |
| 5{{d2}} | ||
| | style="background:silver;"| '''7''' | | style="background:silver;"| '''7''' | ||
| | 7 | | 7 | ||
| | style="background:silver;"| '''0.7''' | | style="background:silver;"| '''0.7''' | ||
| | 0 |
| 0;8{{overline|4972}} | ||
| | style="background:silver;"| '''0.07''' | |||
| | 0.0{{overline|ᘔ0Ɛ62ᘔ68781Ɛ05915343}} | |||
| |- | |- | ||
| | style="background:silver;"| '''800,000''' | |||
| | 326,Ɛ68 | |||
| | style="background:silver;"| '''80,000''' | | style="background:silver;"| '''80,000''' | ||
| | |
| 3{{d2}},368 | ||
| | style="background:silver;"| '''8,000''' | | style="background:silver;"| '''8,000''' | ||
| | 4,768 | | 4,768 | ||
| Line 526: | Line 776: | ||
| | 8 | | 8 | ||
| | style="background:silver;"| '''0.8''' | | style="background:silver;"| '''0.8''' | ||
| | 0 |
| 0;{{overline|9724}} | ||
| | style="background:silver;"| '''0.08''' | |||
| | 0.{{overline|0Ɛ62ᘔ68781Ɛ05915343ᘔ}} | |||
| |- | |- | ||
| | style="background:silver;"| '''900,000''' | |||
| | 374,ᘔ00 | |||
| | style="background:silver;"| '''90,000''' | | style="background:silver;"| '''90,000''' | ||
| | 44,100 | | 44,100 | ||
| Line 543: | Line 789: | ||
| | 9 | | 9 | ||
| | style="background:silver;"| '''0.9''' | | style="background:silver;"| '''0.9''' | ||
| | 0 |
| 0;{{d2}}{{overline|9724}} | ||
| | style="background:silver;"| '''0.09''' | |||
| | 0.1{{overline|0Ɛ62ᘔ68781Ɛ05915343ᘔ}} | |||
| |} | |} | ||
| == Fractions and irrational numbers == | |||
| === Conversion of powers === | |||
| === Fractions === | |||
| {|class="wikitable" | |||
| Duodecimal ] for rational numbers with ] denominators terminate: | |||
| |- | |||
| * {{sfrac|2}} = 0;6 | |||
| | rowspan="2" | ''Exponent'' | |||
| * {{sfrac|3}} = 0;4 | |||
| | colspan="2" | b=2 | |||
| * {{sfrac|4}} = 0;3 | |||
| | colspan="2" | b=3 | |||
| * {{sfrac|6}} = 0;2 | |||
| | colspan="2" | b=4 | |||
| * {{sfrac|8}} = 0;16 | |||
| | colspan="2" | b=5 | |||
| * {{sfrac|9}} = 0;14 | |||
| | colspan="2" | b=6 | |||
| * {{sfrac|10}} = 0;1 (this is one twelfth, {{sfrac|{{d2}}}} is one tenth) | |||
| | colspan="2" | b=7 | |||
| * {{sfrac|14}} = 0;09 (this is one sixteenth, {{sfrac|12}} is one fourteenth) | |||
| |- | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| |- | |||
| | b<sup>6</sup> | |||
| | style="background:silver;"| '''64''' | |||
| | 54 | |||
| | style="background:silver;"| '''729''' | |||
| | 509 | |||
| | style="background:silver;"| '''4,096''' | |||
| | 2454 | |||
| | style="background:silver;"| '''15,625''' | |||
| | 9,061 | |||
| | style="background:silver;"| '''46,656''' | |||
| | 23,000 | |||
| | style="background:silver;"| '''117,649''' | |||
| | 58,101 | |||
| |- | |||
| | b<sup>5</sup> | |||
| | style="background:silver;"| '''32''' | |||
| | 28 | |||
| | style="background:silver;"| '''243''' | |||
| | 183 | |||
| | style="background:silver;"| '''1,024''' | |||
| | 714 | |||
| | style="background:silver;"| '''3,125''' | |||
| | 1,985 | |||
| | style="background:silver;"| '''7,776''' | |||
| | 4,600 | |||
| | style="background:silver;"| '''16,807''' | |||
| | 9,887 | |||
| |- | |||
| | b<sup>4</sup> | |||
| | style="background:silver;"| '''16''' | |||
| | 14 | |||
| | style="background:silver;"| '''81''' | |||
| | 69 | |||
| | style="background:silver;"| '''256''' | |||
| | 194 | |||
| | style="background:silver;"| '''625''' | |||
| | 441 | |||
| | style="background:silver;"| '''1,296''' | |||
| | 900 | |||
| | style="background:silver;"| '''2,401''' | |||
| | 1,481 | |||
| |- | |||
| | b<sup>3</sup> | |||
| | style="background:silver;"| '''8''' | |||
| | 8 | |||
| | style="background:silver;"| '''27''' | |||
| | 23 | |||
| | style="background:silver;"| '''64''' | |||
| | 54 | |||
| | style="background:silver;"| '''125''' | |||
| | ᘔ5 | |||
| | style="background:silver;"| '''216''' | |||
| | 160 | |||
| | style="background:silver;"| '''343''' | |||
| | 247 | |||
| |- | |||
| | b<sup>2</sup> | |||
| | style="background:silver;"| '''4''' | |||
| | 4 | |||
| | style="background:silver;"| '''9''' | |||
| | 9 | |||
| | style="background:silver;"| '''16''' | |||
| | 14 | |||
| | style="background:silver;"| '''25''' | |||
| | 21 | |||
| | style="background:silver;"| '''36''' | |||
| | 30 | |||
| | style="background:silver;"| '''49''' | |||
| | 41 | |||
| |- | |||
| | b<sup>1</sup> | |||
| | style="background:silver;"| '''2''' | |||
| | 2 | |||
| | style="background:silver;"| '''3''' | |||
| | 3 | |||
| | style="background:silver;"| '''4''' | |||
| | 4 | |||
| | style="background:silver;"| '''5''' | |||
| | 5 | |||
| | style="background:silver;"| '''6''' | |||
| | 6 | |||
| | style="background:silver;"| '''7''' | |||
| | 7 | |||
| |- | |||
| | b<sup>−1</sup> | |||
| | style="background:silver;"| '''0.5''' | |||
| | 0.6 | |||
| | style="background:silver;"| '''0.{{overline|3}}''' | |||
| | 0.4 | |||
| | style="background:silver;"| '''0.25''' | |||
| | 0.3 | |||
| | style="background:silver;"| '''0.2''' | |||
| | 0.{{overline|2497}} | |||
| | style="background:silver;"| '''0.1{{overline|6}}''' | |||
| | 0.2 | |||
| | style="background:silver;"| '''0.{{overline|142857}}''' | |||
| | 0.{{overline|186ᘔ35}} | |||
| |- | |||
| | b<sup>−2</sup> | |||
| | style="background:silver;"| '''0.25''' | |||
| | 0.3 | |||
| | style="background:silver;"| '''0.{{overline|1}}''' | |||
| | 0.14 | |||
| | style="background:silver;"| '''0.0625''' | |||
| | 0.09 | |||
| | style="background:silver;"| '''0.04''' | |||
| | 0.{{overline|05915343ᘔ0<br>Ɛ62ᘔ68781Ɛ}} | |||
| | style="background:silver;"| '''0.02{{overline|7}}''' | |||
| | 0.04 | |||
| | style="background:silver;"| '''0.{{overline|0204081632653<br>06122448979591<br>836734693877551}}''' | |||
| | 0.{{overline|02Ɛ322547ᘔ05ᘔ<br>644ᘔ9380Ɛ908996<br>741Ɛ615771283Ɛ}} | |||
| |} | |||
| while other rational numbers have ] duodecimal fractions: | |||
| {|class="wikitable" | |||
| * {{sfrac|5}} = 0;{{Overline|2497}} | |||
| |- | |||
| * {{sfrac|7}} = 0;{{Overline|186{{D2}}35}} | |||
| | rowspan="2" | ''Exponent'' | |||
| * {{sfrac|{{d2}}}} = 0;1{{Overline|2497}} (one tenth) | |||
| | colspan="2" | b=8 | |||
| * {{sfrac|{{d3}}}} = 0;{{Overline|1}} (one eleventh) | |||
| | colspan="2" | b=9 | |||
| * {{sfrac|11}} = 0;{{Overline|0{{D3}}}} (one thirteenth) | |||
| | colspan="2" | '''b=10''' | |||
| * {{sfrac|12}} = 0;0{{Overline|{{D2}}35186}} (one fourteenth) | |||
| | colspan="2" | b=11 | |||
| * {{sfrac|13}} = 0;0{{Overline|9724}} (one fifteenth) | |||
| | colspan="2" | '''b=12''' | |||
| |- | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| | style="background:silver;"| '''''Dec.''''' | |||
| | ''Duod.'' | |||
| |- | |||
| | b<sup>6</sup> | |||
| | style="background:silver;"| '''262,144''' | |||
| | 107,854 | |||
| | style="background:silver;"| '''531,441''' | |||
| | 217,669 | |||
| | style="background:silver;"| '''1,000,000''' | |||
| | 402,854 | |||
| | style="background:silver;"| '''1,771,561''' | |||
| | 715,261 | |||
| | style="background:silver;"| '''2,985,984''' | |||
| | 1,000,000 | |||
| |- | |||
| | b<sup>5</sup> | |||
| | style="background:silver;"| '''32,768''' | |||
| | 16,Ɛ68 | |||
| | style="background:silver;"| '''59,049''' | |||
| | 2ᘔ,209 | |||
| | style="background:silver;"| '''100,000''' | |||
| | 49,ᘔ54 | |||
| | style="background:silver;"| '''161,051''' | |||
| | 79,24Ɛ | |||
| | style="background:silver;"| '''248,832''' | |||
| | 100,000 | |||
| |- | |||
| | b<sup>4</sup> | |||
| | style="background:silver;"| '''4,096''' | |||
| | 2,454 | |||
| | style="background:silver;"| '''6,561''' | |||
| | 3,969 | |||
| | style="background:silver;"| '''10,000''' | |||
| | 5,954 | |||
| | style="background:silver;"| '''14,641''' | |||
| | 8,581 | |||
| | style="background:silver;"| '''20,736''' | |||
| | 10,000 | |||
| |- | |||
| | b<sup>3</sup> | |||
| | style="background:silver;"| '''512''' | |||
| | 368 | |||
| | style="background:silver;"| '''729''' | |||
| | 509 | |||
| | style="background:silver;"| '''1,000''' | |||
| | 6Ɛ4 | |||
| | style="background:silver;"| '''1,331''' | |||
| | 92Ɛ | |||
| | style="background:silver;"| '''1,728''' | |||
| | 1,000 | |||
| |- | |||
| | b<sup>2</sup> | |||
| | style="background:silver;"| '''64''' | |||
| | 54 | |||
| | style="background:silver;"| '''81''' | |||
| | 69 | |||
| | style="background:silver;"| '''100''' | |||
| | 84 | |||
| | style="background:silver;"| '''121''' | |||
| | ᘔ1 | |||
| | style="background:silver;"| '''144''' | |||
| | 100 | |||
| |- | |||
| | b<sup>1</sup> | |||
| | style="background:silver;"| '''8''' | |||
| | 8 | |||
| | style="background:silver;"| '''9''' | |||
| | 9 | |||
| | style="background:silver;"| '''10''' | |||
| | ᘔ | |||
| | style="background:silver;"| '''11''' | |||
| | Ɛ | |||
| | style="background:silver;"| '''12''' | |||
| | 10 | |||
| |- | |||
| | b<sup>−1</sup> | |||
| | style="background:silver;"| '''0.125''' | |||
| | 0.16 | |||
| | style="background:silver;"| '''0.{{overline|1}}''' | |||
| | 0.14 | |||
| | style="background:silver;"| '''0.1''' | |||
| | 0.1{{overline|2497}} | |||
| | style="background:silver;"| '''0.{{overline|09}}''' | |||
| | 0.{{overline|1}} | |||
| | style="background:silver;"| '''0.08{{overline|3}}''' | |||
| | 0.1 | |||
| |- | |||
| | b<sup>−2</sup> | |||
| | style="background:silver;"| '''0.015625''' | |||
| | 0.023 | |||
| | style="background:silver;"| '''0.{{overline|012345679}}''' | |||
| | 0.0194 | |||
| | style="background:silver;"| '''0.01''' | |||
| | 0.0{{overline|15343ᘔ0Ɛ6<br>2ᘔ68781Ɛ059}} | |||
| | style="background:silver;"| '''0.{{overline|00826446280<br>99173553719}}''' | |||
| | 0.{{overline|0123456789Ɛ}} | |||
| | style="background:silver;"| '''0.0069{{overline|4}}''' | |||
| | 0.01 | |||
| |} | |||
| {| class="wikitable" | |||
| ==Fractions and irrational numbers== | |||
| ! Examples in duodecimal | |||
| ! Decimal equivalent | |||
| ===Fractions=== | |||
| Duodecimal ] may be simple: | |||
| * {{sfrac|2}} = 0.6 | |||
| * {{sfrac|3}} = 0.4 | |||
| * {{sfrac|4}} = 0.3 | |||
| * {{sfrac|6}} = 0.2 | |||
| * {{sfrac|8}} = 0.16 | |||
| * {{sfrac|9}} = 0.14 | |||
| * {{sfrac|10}} = 0.1 | |||
| or complicated: | |||
| * {{sfrac|5}} = 0.24972497... recurring (rounded to 0.24ᘔ) | |||
| * {{sfrac|7}} = 0.186ᘔ35186ᘔ35... recurring (rounded to 0.187) | |||
| * {{sfrac|ᘔ}} = 0.124972497... recurring (rounded to 0.125) | |||
| * {{sfrac|Ɛ}} = 0.111111... recurring (rounded to 0.111) | |||
| * {{sfrac|11}} = 0.0Ɛ0Ɛ0Ɛ... recurring (rounded to 0.0Ɛ1) | |||
| * {{sfrac|12}} = 0.0ᘔ35186ᘔ35186... recurring (rounded to 0.0ᘔ3) | |||
| {|class="wikitable" | |||
| |- | |||
| | ''Examples in duodecimal'' | |||
| | ''Decimal equivalent'' | |||
| |- | |- | ||
| | 1 × |
| 1 × {{sfrac|5|8}} = 0.76 | ||
| | 1 × |
| 1 × {{sfrac|5|8}} = 0.625 | ||
| |- | |- | ||
| | 100 × |
| 100 × {{sfrac|5|8}} = 76 | ||
| | 144 × |
| 144 × {{sfrac|5|8}} = 90 | ||
| |- | |- | ||
| | {{sfrac|576|9}} = 76 | | {{sfrac|576|9}} = 76 | ||
| Line 839: | Line 829: | ||
| | {{sfrac|576|9}} = 64 | | {{sfrac|576|9}} = 64 | ||
| |- | |- | ||
| | |
| 1{{d2}}.6 + 7.6 = 26 | ||
| | 22.5 + 7.5 = 30 | | 22.5 + 7.5 = 30 | ||
| |} | |} | ||
| As explained in ]s, whenever an ] is written in ] notation in any base, the fraction can be expressed exactly (terminates) if and only if all the ]s of its denominator are also prime factors of the base |
As explained in ]s, whenever an ] is written in ] notation in any base, the fraction can be expressed exactly (terminates) if and only if all the ]s of its denominator are also prime factors of the base. | ||
| Because <math>2\times5=10</math> in the decimal system, fractions whose denominators are made up solely of multiples of 2 and 5 terminate: {{sfrac|8}} = {{sfrac|(2×2×2)}}, {{sfrac|20}} = {{sfrac|(2×2×5)}}, and {{sfrac|500}} = {{sfrac|(2×2×5×5×5)}} can be expressed exactly as 0.125, 0.05, and 0.002 respectively. {{sfrac|3}} and {{sfrac|7}}, however, recur (0.333... and 0.142857142857...). | |||
| The number of denominators which give terminating fractions within a given number of digits, say ''n'', in a base ''b'' is the number of factors (divisors) of ''b<sup>n</sup>'', the ''n''th power of the base ''b'' (although this includes the divisor 1, which does not produce fractions when used as the denominator). The number of factors of ''b<sup>n</sup>'' is given using its prime factorization. | |||
| Because <math>2\times2\times3=12</math> in the duodecimal system, {{sfrac|8}} is exact; {{sfrac|20}} and {{sfrac|500}} recur because they include 5 as a factor; {{sfrac|3}} is exact, and {{sfrac|7}} recurs, just as it does in decimal. | |||
| For decimal, 10<sup>''n''</sup> = 2<sup>''n''</sup> * 5<sup>''n''</sup>. The number of divisors is found by adding one to each exponent of each prime and multiplying the resulting quantities together. | |||
| Factors of 10<sup>''n''</sup> = (''n''+1)(''n''+1) = (''n''+1)<sup>2</sup>. | |||
| The number of denominators that give terminating fractions within a given number of digits, {{math|''n''}}, in a base {{math|''b''}} is the number of factors (divisors) of <math>b^n</math>, the {{math|''n''}}th power of the base {{math|''b''}} (although this includes the divisor 1, which does not produce fractions when used as the denominator). The number of factors of ''<math>b^n</math>'' is given using its prime factorization. | |||
| For example, the number 8 is a factor of 10<sup>3</sup> (1000), so 1/8 and other fractions with a denominator of 8 can not require more than 3 fractional decimal digits to terminate. 5/8 = 0.625<sub>ten</sub> | |||
| For decimal, <math>10^n=2^n\times 5^n</math>. The number of divisors is found by adding one to each exponent of each prime and multiplying the resulting quantities together, so the number of factors of ''<math>10^n</math>'' is <math>(n+1)(n+1)=(n+1)^2</math>. | |||
| For duodecimal, 12<sup>''n''</sup> = 2<sup>2''n''</sup> * 3<sup>''n''</sup>. This has (2''n''+1)(''n''+1) divisors. The sample denominator of 8 is a factor of a gross (12<sup>2</sup> = 144), so eighths can not need more than two duodecimal fractional places to terminate. 5/8 = 0.76<sub>twelve</sub> | |||
| For example, the number 8 is a factor of 10<sup>3</sup> (1000), so <math display="inline">\frac{1}{8}</math> and other fractions with a denominator of 8 cannot require more than three fractional decimal digits to terminate. <math display="inline">\frac{5}{8}=0.625_{10}.</math> | |||
| Because both ten and twelve have two unique prime factors, the number of divisors of ''b<sup>n</sup>'' for ''b'' = 10 or 12 grows quadratically with the exponent ''n'' (in other words, of the order of ''n''<sup>2</sup>). | |||
| For duodecimal, <math>10^n=2^{2n}\times 3^n</math>. This has <math>(2n+1)(n+1)</math> divisors. The sample denominator of 8 is a factor of a gross <math display="inline">12^2=144</math> (in decimal), so eighths cannot need more than two duodecimal fractional places to terminate. <math display="inline">\frac{5}{8}=0.76_{12}.</math> | |||
| Because both ten and twelve have two unique prime factors, the number of divisors of ''<math>b^n</math>'' for {{math|''b'' {{=}} 10 or 12}} grows quadratically with the exponent {{math|''n''}} (in other words, of the order of <math>n^2</math>). | |||
| === Recurring digits === | === Recurring digits === | ||
| The Dozenal Society of America argues that factors of 3 are more commonly encountered in real-life ] problems than factors of 5.<ref name="dsafaq">{{cite web |author=De Vlieger |first=Michael Thomas |date=30 November 2011 |title=Dozenal FAQs |url=https://dozenal.org/articles/DSA-DozenalFAQs.pdf |access-date=November 20, 2022 |website=dozenal.org |publisher=The Dozenal Society of America }}</ref> Thus, in practical applications, the nuisance of ] is encountered less often when duodecimal notation is used. Advocates of duodecimal systems argue that this is particularly true of financial calculations, in which the twelve months of the year often enter into calculations. | |||
| However, when recurring fractions ''do'' occur in duodecimal notation, they are less likely to have a very short period than in decimal notation, because ] (twelve) is between two ]s, ] (eleven) and ] (thirteen), whereas ten is adjacent to the ] ]. Nonetheless, having a shorter or longer period does not help the main inconvenience that one does not get a finite representation for such fractions in the given base (so ], which introduces inexactitude, is necessary to handle them in calculations), and overall one is more likely to have to deal with infinite recurring digits when fractions are expressed in decimal than in duodecimal, because one out of every three consecutive numbers contains the prime factor ] in its factorization, whereas only one out of every five contains the prime factor ]. All other prime factors, except 2, are not shared by either ten or twelve, so they do not | |||
| influence the relative likeliness of encountering recurring digits (any irreducible fraction that contains any of these other factors in its denominator will recur in either base). | |||
| Also, the prime factor ] appears twice in the factorization of twelve, whereas only once in the factorization of ten; which means that most fractions whose denominators are ] will have a shorter, more convenient terminating representation in duodecimal than in decimal: | |||
| However, when recurring fractions ''do'' occur in duodecimal notation, they are less likely to have a very short period than in decimal notation, because ] (twelve) is between two ]s, ] (eleven) and ] (thirteen), whereas ten is adjacent to the ] ]. Nonetheless, having a shorter or longer period doesn't help the main inconvenience that one does not get a finite representation for such fractions in the given base (so ], which introduces inexactitude, is necessary to handle them in calculations), and overall one is more likely to have to deal with infinite recurring digits when fractions are expressed in decimal than in duodecimal, because one out of every three consecutive numbers contains the prime factor ] in its factorization, whereas only one out of every five contains the prime factor ]. All other prime factors, except 2, are not shared by either ten or twelve, so they do not | |||
| influence the relative likeliness of encountering recurring digits (any irreducible fraction that contains any of these other factors in its denominator will recur in either base). Also, the prime factor ] appears twice in the factorization of twelve, whereas only once in the factorization of ten; which means that most fractions whose denominators are ] will have a shorter, more convenient terminating representation in duodecimal than in decimal representation (e.g. 1/(2<sup>2</sup>) = 0.25 <sub>ten</sub> = 0.3 <sub>twelve</sub>; 1/(2<sup>3</sup>) = 0.125 <sub>ten</sub> = 0.16 <sub>twelve</sub>; 1/(2<sup>4</sup>) = 0.0625 <sub>ten</sub> = 0.09 <sub>twelve</sub>; 1/(2<sup>5</sup>) = 0.03125 <sub>ten</sub> = 0.046 <sub>twelve</sub>; etc.). | |||
| * 1/(2<sup>2</sup>) = 0.25<sub>10</sub> = 0.3<sub>12</sub> | |||
| Values in '''bold''' indicate that value is exact. | |||
| * 1/(2<sup>3</sup>) = 0.125<sub>10</sub> = 0.16<sub>12</sub> | |||
| * 1/(2<sup>4</sup>) = 0.0625<sub>10</sub> = 0.09<sub>12</sub> | |||
| * 1/(2<sup>5</sup>) = 0.03125<sub>10</sub> = 0.046<sub>12</sub> | |||
| {|class="wikitable" | {| class="wikitable" | ||
| |- style="text-align:center;" |
|- style="text-align:center;" | ||
| | colspan="3"| '''Decimal base'''<br><SMALL>Prime factors of the base: <span style="color:Green">'''2'''</span>, <span style="color:Green">'''5'''</span></SMALL><br><SMALL>Prime factors of one below the base: <span style="color:Blue">'''3'''</span></SMALL><br><SMALL>Prime factors of one above the base: <span style="color: |
| colspan="3"| '''Decimal base'''<br><SMALL>Prime factors of the base: <span style="color:Green">'''2'''</span>, <span style="color:Green">'''5'''</span></SMALL><br><SMALL>Prime factors of one below the base: <span style="color:Blue">'''3'''</span></SMALL><br><SMALL>Prime factors of one above the base: <span style="color:Magenta">'''11'''</span></SMALL><br><SMALL>All other primes: <span style="color:Red">'''7'''</span>, <span style="color:Red">'''13'''</span>, <span style="color:Red">'''17'''</span>, <span style="color:Red">'''19'''</span>, <span style="color:Red">'''23'''</span>, <span style="color:Red">'''29'''</span>, <span style="color:Red">'''31'''</span></SMALL> | ||
| | colspan="3"| '''Duodecimal base'''<br><SMALL>Prime factors of the base: <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span></SMALL><br><SMALL>Prime factors of one below the base: <span style="color:Blue">''' |
| colspan="3"| '''Duodecimal base'''<br><SMALL>Prime factors of the base: <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span></SMALL><br><SMALL>Prime factors of one below the base: <span style="color:Blue">'''{{d3}}'''</span></SMALL><br><SMALL>Prime factors of one above the base: <span style="color:Magenta">'''11 (=13<sub>10</sub>)'''</span></SMALL><br><SMALL>All other primes: <span style="color:Red">'''5'''</span>, <span style="color:Red">'''7'''</span>, <span style="color:Red">'''15 (=17<sub>10</sub>)'''</span>, <span style="color:Red">'''17 (=19<sub>10</sub>)'''</span>, <span style="color:Red">'''1{{d3}} (=23<sub>10</sub>)'''</span>, <span style="color:Red">'''25 (=29<sub>10</sub>)'''</span>, <span style="color:Red">'''27 (=31<sub>10</sub>)'''</span></SMALL> | ||
| |- | |||
| |- style="text-align:center;" | |||
| ! Fraction | |||
| ! <SMALL>Prime factors<br>of the denominator</SMALL> | |||
| ! Positional representation | |||
| ! Positional representation | |||
| ! <SMALL>Prime factors<br>of the denominator</SMALL> | |||
| ! Fraction | |||
| |- | |- | ||
| | style="text-align:center;"| 1/2 | | style="text-align:center;"| 1/2 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span> | ||
| | |
| 0.5 | ||
| | |
| 0;6 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span> | ||
| | style="text-align:center;"| 1/2 | | style="text-align:center;"| 1/2 | ||
| Line 885: | Line 883: | ||
| | style="text-align:center;"| 1/3 | | style="text-align:center;"| 1/3 | ||
| | style="text-align:center;"| <span style="color:Blue">'''3'''</span> | | style="text-align:center;"| <span style="color:Blue">'''3'''</span> | ||
| | |
| 0.{{overline|3}} | ||
| | |
| 0;4 | ||
| | style="text-align:center;"| <span style="color:Green">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''3'''</span> | ||
| | style="text-align:center;"| 1/3 | | style="text-align:center;"| 1/3 | ||
| Line 892: | Line 890: | ||
| | style="text-align:center;"| 1/4 | | style="text-align:center;"| 1/4 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span> | ||
| | |
| 0.25 | ||
| | |
| 0;3 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span> | ||
| | style="text-align:center;"| 1/4 | | style="text-align:center;"| 1/4 | ||
| Line 899: | Line 897: | ||
| | style="text-align:center;"| 1/5 | | style="text-align:center;"| 1/5 | ||
| | style="text-align:center;"| <span style="color:Green">'''5'''</span> | | style="text-align:center;"| <span style="color:Green">'''5'''</span> | ||
| | |
| 0.2 | ||
| | |
| 0;{{overline|2497}} | ||
| | style="text-align:center;"| <span style="color:Red">'''5'''</span> | | style="text-align:center;"| <span style="color:Red">'''5'''</span> | ||
| | style="text-align:center;"| 1/5 | | style="text-align:center;"| 1/5 | ||
| Line 906: | Line 904: | ||
| | style="text-align:center;"| 1/6 | | style="text-align:center;"| 1/6 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span> | ||
| | |
| 0.1{{overline|6}} | ||
| | |
| 0;2 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span> | ||
| | style="text-align:center;"| 1/6 | | style="text-align:center;"| 1/6 | ||
| Line 913: | Line 911: | ||
| | style="text-align:center;"| 1/7 | | style="text-align:center;"| 1/7 | ||
| | style="text-align:center;"| <span style="color:Red">'''7'''</span> | | style="text-align:center;"| <span style="color:Red">'''7'''</span> | ||
| | |
| 0.{{overline|142857}} | ||
| | |
| 0;{{overline|186{{d2}}35}} | ||
| | style="text-align:center;"| <span style="color:Red">'''7'''</span> | | style="text-align:center;"| <span style="color:Red">'''7'''</span> | ||
| | style="text-align:center;"| 1/7 | | style="text-align:center;"| 1/7 | ||
| Line 920: | Line 918: | ||
| | style="text-align:center;"| 1/8 | | style="text-align:center;"| 1/8 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span> | ||
| | |
| 0.125 | ||
| | |
| 0;16 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span> | ||
| | style="text-align:center;"| 1/8 | | style="text-align:center;"| 1/8 | ||
| Line 927: | Line 925: | ||
| | style="text-align:center;"| 1/9 | | style="text-align:center;"| 1/9 | ||
| | style="text-align:center;"| <span style="color:Blue">'''3'''</span> | | style="text-align:center;"| <span style="color:Blue">'''3'''</span> | ||
| | |
| 0.{{overline|1}} | ||
| | |
| 0;14 | ||
| | style="text-align:center;"| <span style="color:Green">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''3'''</span> | ||
| | style="text-align:center;"| 1/9 | | style="text-align:center;"| 1/9 | ||
| Line 934: | Line 932: | ||
| | style="text-align:center;"| 1/10 | | style="text-align:center;"| 1/10 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''5'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''5'''</span> | ||
| | |
| 0.1 | ||
| | |
| 0;1{{overline|2497}} | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''5'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''5'''</span> | ||
| | style="text-align:center;"| 1/ |
| style="text-align:center;"| 1/{{d2}} | ||
| |- | |- | ||
| | style="text-align:center;"| 1/11 | | style="text-align:center;"| 1/11 | ||
| | style="text-align:center;"| <span style="color: |
| style="text-align:center;"| <span style="color:Magenta">'''11'''</span> | ||
| | |
| 0.{{overline|09}} | ||
| | |
| 0;{{overline|1}} | ||
| | style="text-align:center;"| <span style="color:Blue">''' |
| style="text-align:center;"| <span style="color:Blue">'''{{d3}}'''</span> | ||
| | style="text-align:center;"| 1/ |
| style="text-align:center;"| 1/{{d3}} | ||
| |- | |- | ||
| | style="text-align:center;"| 1/12 | | style="text-align:center;"| 1/12 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span> | ||
| | |
| 0.08{{overline|3}} | ||
| | |
| 0;1 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span> | ||
| | style="text-align:center;"| 1/10 | | style="text-align:center;"| 1/10 | ||
| Line 955: | Line 953: | ||
| | style="text-align:center;"| 1/13 | | style="text-align:center;"| 1/13 | ||
| | style="text-align:center;"| <span style="color:Red">'''13'''</span> | | style="text-align:center;"| <span style="color:Red">'''13'''</span> | ||
| | |
| 0.{{overline|076923}} | ||
| | |
| 0;{{overline|0{{d3}}}} | ||
| | style="text-align:center;"| <span style="color: |
| style="text-align:center;"| <span style="color:Magenta">'''11'''</span> | ||
| | style="text-align:center;"| 1/11 | | style="text-align:center;"| 1/11 | ||
| |- | |- | ||
| | style="text-align:center;"| 1/14 | | style="text-align:center;"| 1/14 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''7'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''7'''</span> | ||
| | |
| 0.0{{overline|714285}} | ||
| | |
| 0;0{{overline|{{d2}}35186}} | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''7'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''7'''</span> | ||
| | style="text-align:center;"| 1/12 | | style="text-align:center;"| 1/12 | ||
| Line 969: | Line 967: | ||
| | style="text-align:center;"| 1/15 | | style="text-align:center;"| 1/15 | ||
| | style="text-align:center;"| <span style="color:Blue">'''3'''</span>, <span style="color:Green">'''5'''</span> | | style="text-align:center;"| <span style="color:Blue">'''3'''</span>, <span style="color:Green">'''5'''</span> | ||
| | |
| 0.0{{overline|6}} | ||
| | |
| 0;0{{overline|9724}} | ||
| | style="text-align:center;"| <span style="color:Green">'''3'''</span>, <span style="color:Red">'''5'''</span> | | style="text-align:center;"| <span style="color:Green">'''3'''</span>, <span style="color:Red">'''5'''</span> | ||
| | style="text-align:center;"| 1/13 | | style="text-align:center;"| 1/13 | ||
| Line 976: | Line 974: | ||
| | style="text-align:center;"| 1/16 | | style="text-align:center;"| 1/16 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span> | ||
| | |
| 0.0625 | ||
| | |
| 0;09 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span> | ||
| | style="text-align:center;"| 1/14 | | style="text-align:center;"| 1/14 | ||
| Line 983: | Line 981: | ||
| | style="text-align:center;"| 1/17 | | style="text-align:center;"| 1/17 | ||
| | style="text-align:center;"| <span style="color:Red">'''17'''</span> | | style="text-align:center;"| <span style="color:Red">'''17'''</span> | ||
| | |
| 0.{{overline|0588235294117647}} | ||
| | |
| 0;{{overline|08579214{{d3}}36429{{d2}}7}} | ||
| | style="text-align:center;"| <span style="color:Red">'''15'''</span> | | style="text-align:center;"| <span style="color:Red">'''15'''</span> | ||
| | style="text-align:center;"| 1/15 | | style="text-align:center;"| 1/15 | ||
| Line 990: | Line 988: | ||
| | style="text-align:center;"| 1/18 | | style="text-align:center;"| 1/18 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span> | ||
| | |
| 0.0{{overline|5}} | ||
| | |
| 0;08 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span> | ||
| | style="text-align:center;"| 1/16 | | style="text-align:center;"| 1/16 | ||
| Line 997: | Line 995: | ||
| | style="text-align:center;"| 1/19 | | style="text-align:center;"| 1/19 | ||
| | style="text-align:center;"| <span style="color:Red">'''19'''</span> | | style="text-align:center;"| <span style="color:Red">'''19'''</span> | ||
| | |
| 0.{{overline|052631578947368421}} | ||
| | |
| 0;{{overline|076{{d3}}45}} | ||
| | style="text-align:center;"| <span style="color:Red">'''17'''</span> | | style="text-align:center;"| <span style="color:Red">'''17'''</span> | ||
| | style="text-align:center;"| 1/17 | | style="text-align:center;"| 1/17 | ||
| Line 1,004: | Line 1,002: | ||
| | style="text-align:center;"| 1/20 | | style="text-align:center;"| 1/20 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''5'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''5'''</span> | ||
| | |
| 0.05 | ||
| | |
| 0;0{{overline|7249}} | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''5'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''5'''</span> | ||
| | style="text-align:center;"| 1/18 | | style="text-align:center;"| 1/18 | ||
| Line 1,011: | Line 1,009: | ||
| | style="text-align:center;"| 1/21 | | style="text-align:center;"| 1/21 | ||
| | style="text-align:center;"| <span style="color:Blue">'''3'''</span>, <span style="color:Red">'''7'''</span> | | style="text-align:center;"| <span style="color:Blue">'''3'''</span>, <span style="color:Red">'''7'''</span> | ||
| | |
| 0.{{overline|047619}} | ||
| | |
| 0;0{{overline|6{{d2}}3518}} | ||
| | style="text-align:center;"| <span style="color:Green">'''3'''</span>, <span style="color:Red">'''7'''</span> | | style="text-align:center;"| <span style="color:Green">'''3'''</span>, <span style="color:Red">'''7'''</span> | ||
| | style="text-align:center;"| 1/19 | | style="text-align:center;"| 1/19 | ||
| |- | |- | ||
| | style="text-align:center;"| 1/22 | | style="text-align:center;"| 1/22 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color: |
| style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Magenta">'''11'''</span> | ||
| | |
| 0.0{{overline|45}} | ||
| | |
| 0;0{{overline|6}} | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">''' |
| style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''{{d3}}'''</span> | ||
| | style="text-align:center;"| 1/ |
| style="text-align:center;"| 1/1{{d2}} | ||
| |- | |- | ||
| | style="text-align:center;"| 1/23 | | style="text-align:center;"| 1/23 | ||
| | style="text-align:center;"| <span style="color:Red">'''23'''</span> | | style="text-align:center;"| <span style="color:Red">'''23'''</span> | ||
| | |
| 0.{{overline|0434782608695652173913}} | ||
| | |
| 0;{{overline|06316948421}} | ||
| | style="text-align:center;"| <span style="color:Red">''' |
| style="text-align:center;"| <span style="color:Red">'''1{{d3}}'''</span> | ||
| | style="text-align:center;"| 1/ |
| style="text-align:center;"| 1/1{{d3}} | ||
| |- | |- | ||
| | style="text-align:center;"| 1/24 | | style="text-align:center;"| 1/24 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span> | ||
| | |
| 0.041{{overline|6}} | ||
| | |
| 0;06 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span> | ||
| | style="text-align:center;"| 1/20 | | style="text-align:center;"| 1/20 | ||
| Line 1,039: | Line 1,037: | ||
| | style="text-align:center;"| 1/25 | | style="text-align:center;"| 1/25 | ||
| | style="text-align:center;"| <span style="color:Green">'''5'''</span> | | style="text-align:center;"| <span style="color:Green">'''5'''</span> | ||
| | |
| 0.04 | ||
| | 0;{{overline|05915343{{d2}}0{{d3}}62{{d2}}68781{{d3}}}} | |||
| | style="background:silver;"| '''0.'''{{overline|05915343ᘔ0Ɛ62ᘔ68781Ɛ}} | |||
| | style="text-align:center;"| <span style="color:Red">'''5'''</span> | | style="text-align:center;"| <span style="color:Red">'''5'''</span> | ||
| | style="text-align:center;"| 1/21 | | style="text-align:center;"| 1/21 | ||
| Line 1,046: | Line 1,044: | ||
| | style="text-align:center;"| 1/26 | | style="text-align:center;"| 1/26 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''13'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''13'''</span> | ||
| | |
| 0.0{{overline|384615}} | ||
| | |
| 0;0{{overline|56}} | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color: |
| style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Magenta">'''11'''</span> | ||
| | style="text-align:center;"| 1/22 | | style="text-align:center;"| 1/22 | ||
| |- | |- | ||
| | style="text-align:center;"| 1/27 | | style="text-align:center;"| 1/27 | ||
| | style="text-align:center;"| <span style="color:Blue">'''3'''</span> | | style="text-align:center;"| <span style="color:Blue">'''3'''</span> | ||
| | |
| 0.{{overline|037}} | ||
| | |
| 0;054 | ||
| | style="text-align:center;"| <span style="color:Green">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''3'''</span> | ||
| | style="text-align:center;"| 1/23 | | style="text-align:center;"| 1/23 | ||
| Line 1,060: | Line 1,058: | ||
| | style="text-align:center;"| 1/28 | | style="text-align:center;"| 1/28 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''7'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''7'''</span> | ||
| | |
| 0.03{{overline|571428}} | ||
| | |
| 0;0{{overline|5186{{d2}}3}} | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''7'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''7'''</span> | ||
| | style="text-align:center;"| 1/24 | | style="text-align:center;"| 1/24 | ||
| Line 1,067: | Line 1,065: | ||
| | style="text-align:center;"| 1/29 | | style="text-align:center;"| 1/29 | ||
| | style="text-align:center;"| <span style="color:Red">'''29'''</span> | | style="text-align:center;"| <span style="color:Red">'''29'''</span> | ||
| | |
| 0.{{overline|0344827586206896551724137931}} | ||
| | |
| 0;{{overline|04{{d3}}7}} | ||
| | style="text-align:center;"| <span style="color:Red">'''25'''</span> | | style="text-align:center;"| <span style="color:Red">'''25'''</span> | ||
| | style="text-align:center;"| 1/25 | | style="text-align:center;"| 1/25 | ||
| Line 1,074: | Line 1,072: | ||
| | style="text-align:center;"| 1/30 | | style="text-align:center;"| 1/30 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span>, <span style="color:Green">'''5'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span>, <span style="color:Green">'''5'''</span> | ||
| | |
| 0.0{{overline|3}} | ||
| | |
| 0;0{{overline|4972}} | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span>, <span style="color:Red">'''5'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span>, <span style="color:Red">'''5'''</span> | ||
| | style="text-align:center;"| 1/26 | | style="text-align:center;"| 1/26 | ||
| Line 1,081: | Line 1,079: | ||
| | style="text-align:center;"| 1/31 | | style="text-align:center;"| 1/31 | ||
| | style="text-align:center;"| <span style="color:Red">'''31'''</span> | | style="text-align:center;"| <span style="color:Red">'''31'''</span> | ||
| | |
| 0.{{overline|032258064516129}} | ||
| | 0;{{overline|0478{{d2}}{{d2}}093598166{{d3}}74311{{d3}}28623{{d2}}55}} | |||
| | style="background:silver;"| '''0.'''{{overline|0478ᘔᘔ093598166Ɛ74311Ɛ28623ᘔ55}} | |||
| | style="text-align:center;"| <span style="color:Red">'''27'''</span> | | style="text-align:center;"| <span style="color:Red">'''27'''</span> | ||
| | style="text-align:center;"| 1/27 | | style="text-align:center;"| 1/27 | ||
| Line 1,088: | Line 1,086: | ||
| | style="text-align:center;"| 1/32 | | style="text-align:center;"| 1/32 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span> | ||
| | |
| 0.03125 | ||
| | |
| 0;046 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span> | ||
| | style="text-align:center;"| 1/28 | | style="text-align:center;"| 1/28 | ||
| |- | |- | ||
| | style="text-align:center;"| 1/33 | | style="text-align:center;"| 1/33 | ||
| | style="text-align:center;"| <span style="color:Blue">'''3'''</span>, <span style="color: |
| style="text-align:center;"| <span style="color:Blue">'''3'''</span>, <span style="color:Magenta">'''11'''</span> | ||
| | |
| 0.{{overline|03}} | ||
| | |
| 0;0{{overline|4}} | ||
| | style="text-align:center;"| <span style="color:Green">'''3'''</span>, <span style="color:Blue">''' |
| style="text-align:center;"| <span style="color:Green">'''3'''</span>, <span style="color:Blue">'''{{d3}}'''</span> | ||
| | style="text-align:center;"| 1/29 | | style="text-align:center;"| 1/29 | ||
| |- | |- | ||
| | style="text-align:center;"| 1/34 | | style="text-align:center;"| 1/34 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''17'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''17'''</span> | ||
| | |
| 0.0{{overline|2941176470588235}} | ||
| | |
| 0;0{{overline|429{{d2}}708579214{{d3}}36}} | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''15'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Red">'''15'''</span> | ||
| | style="text-align:center;"| 1/ |
| style="text-align:center;"| 1/2{{d2}} | ||
| |- | |- | ||
| | style="text-align:center;"| 1/35 | | style="text-align:center;"| 1/35 | ||
| | style="text-align:center;"| <span style="color:Green">'''5'''</span>, <span style="color:Red">'''7'''</span> | | style="text-align:center;"| <span style="color:Green">'''5'''</span>, <span style="color:Red">'''7'''</span> | ||
| | |
| 0.0{{overline|285714}} | ||
| | |
| 0;{{overline|0414559{{d3}}3931}} | ||
| | style="text-align:center;"| <span style="color:Red">'''5'''</span>, <span style="color:Red">'''7'''</span> | | style="text-align:center;"| <span style="color:Red">'''5'''</span>, <span style="color:Red">'''7'''</span> | ||
| | style="text-align:center;"| 1/ |
| style="text-align:center;"| 1/2{{d3}} | ||
| |- | |- | ||
| | style="text-align:center;"| 1/36 | | style="text-align:center;"| 1/36 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Blue">'''3'''</span> | ||
| | |
| 0.02{{overline|7}} | ||
| | |
| 0;04 | ||
| | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span> | | style="text-align:center;"| <span style="color:Green">'''2'''</span>, <span style="color:Green">'''3'''</span> | ||
| | style="text-align:center;"| 1/30 | | style="text-align:center;"| 1/30 | ||
| |} | |} | ||
| The duodecimal period length of 1/''n'' are | The duodecimal period length of 1/''n'' are (in decimal) | ||
| :0, 0, 0, 0, 4, 0, 6, 0, 0, 4, 1, 0, 2, 6, 4, 0, 16, 0, 6, 4, 6, 1, 11, 0, 20, 2, 0, 6, 4, 4, 30, 0, 1, 16, 12, 0, 9, 6, 2, 4, 40, 6, 42, 1, 4, 11, 23, 0, 42, 20, 16, 2, 52, 0, 4, 6, 6, 4, 29, 4, 15, 30, 6, 0, 4, 1, 66, 16, 11, 12, 35, 0, ... {{OEIS|id=A246004}} | :0, 0, 0, 0, 4, 0, 6, 0, 0, 4, 1, 0, 2, 6, 4, 0, 16, 0, 6, 4, 6, 1, 11, 0, 20, 2, 0, 6, 4, 4, 30, 0, 1, 16, 12, 0, 9, 6, 2, 4, 40, 6, 42, 1, 4, 11, 23, 0, 42, 20, 16, 2, 52, 0, 4, 6, 6, 4, 29, 4, 15, 30, 6, 0, 4, 1, 66, 16, 11, 12, 35, 0, ... {{OEIS|id=A246004}} | ||
| The duodecimal period length of 1/(''n''th prime) are | The duodecimal period length of 1/(''n''th prime) are (in decimal) | ||
| :0, 0, 4, 6, 1, 2, 16, 6, 11, 4, 30, 9, 40, 42, 23, 52, 29, 15, 66, 35, 36, 26, 41, 8, 16, 100, 102, 53, 54, 112, 126, 65, 136, 138, 148, 150, 3, 162, 83, 172, 89, 90, 95, 24, 196, 66, 14, 222, 113, 114, 8, 119, 120, 125, 256, 131, 268, 54, 138, 280, ... {{OEIS|id=A246489}} | :0, 0, 4, 6, 1, 2, 16, 6, 11, 4, 30, 9, 40, 42, 23, 52, 29, 15, 66, 35, 36, 26, 41, 8, 16, 100, 102, 53, 54, 112, 126, 65, 136, 138, 148, 150, 3, 162, 83, 172, 89, 90, 95, 24, 196, 66, 14, 222, 113, 114, 8, 119, 120, 125, 256, 131, 268, 54, 138, 280, ... {{OEIS|id=A246489}} | ||
| Smallest prime with duodecimal period ''n'' are | Smallest prime with duodecimal period ''n'' are (in decimal) | ||
| :11, 13, 157, 5, 22621, 7, 659, 89, 37, 19141, 23, 20593, 477517, 211, 61, 17, 2693651, 1657, 29043636306420266077, 85403261, 8177824843189, 57154490053, 47, 193, 303551, 79, 306829, 673, 59, 31, 373, 153953, 886381, 2551, 71, 73, ... {{OEIS|id=A252170}} | :11, 13, 157, 5, 22621, 7, 659, 89, 37, 19141, 23, 20593, 477517, 211, 61, 17, 2693651, 1657, 29043636306420266077, 85403261, 8177824843189, 57154490053, 47, 193, 303551, 79, 306829, 673, 59, 31, 373, 153953, 886381, 2551, 71, 73, ... {{OEIS|id=A252170}} | ||
| === Irrational numbers === | === Irrational numbers === | ||
| The representations of ]s in any positional number system (including decimal and duodecimal) neither terminate nor ]. The following table gives the first digits for some important ] and ] numbers in both decimal and duodecimal. | |||
| As for ]s, none of them have a finite representation in ''any'' of the ]-based positional number systems (such as the decimal and duodecimal ones); this is because a rational-based positional number system is essentially nothing but a way of expressing quantities as a sum of fractions whose denominators are powers of the base, and by definition no ''finite'' sum of rational numbers can ever result in an irrational number. For example, 123.456 = 1 × 10<sup>2</sup> + 2 × 10<sup>1</sup> + 3 × 10<sup>0</sup> + 4 × 1/10<sup>1</sup> + 5 × 1/10<sup>2</sup> + 6 × 1/10<sup>3</sup> (this is also the reason why fractions that contain prime factors in their denominator not in common with those of the base do not have a terminating representation in that base). Moreover, the infinite series of digits of an irrational number does not exhibit a pattern of repetition; instead, the different digits succeed in a seemingly random fashion. The following chart compares the first few digits of the decimal and duodecimal representation of several of the most important ] and ] irrational numbers. Some of these numbers may be perceived as having fortuitous patterns, making them easier to memorize, when represented in one base or the other. | |||
| {|class="wikitable" | {| class="wikitable" | ||
| ! Algebraic irrational number | |||
| |- style="text-align:center;" | |||
| ! In decimal | |||
| || ''Algebraic irrational number'' | |||
| ! In duodecimal | |||
| || '''In duodecimal''' | |||
| |- | |- | ||
| | style="text-align:center;"| ] |
| style="text-align:center;"| ], the square root of 2 | ||
| | 1. |
| 1.414213562373... | ||
| | 1;4{{d3}}79170{{d2}}07{{d3}}8... | |||
| | 1.4Ɛ79170ᘔ07Ɛ857... (≈ 1.5) | |||
| |- | |- | ||
| | style="text-align:center;"| ] |
| style="text-align:center;"| {{mvar|]}} (phi), the golden ratio = <math>\tfrac{1+\sqrt{5}}{2}</math> | ||
| | 1. |
| 1.618033988749... | ||
| | 1;74{{d3}}{{d3}}6772802{{d2}}... | |||
| | 1.894Ɛ97ƐƐ968704... (≈ 1.895) | |||
| |- | |- | ||
| ! Transcendental number | |||
| | style="text-align:center;"| ] <SMALL>(the length of the ] of a 1×2 ])</SMALL> | |||
| ! In decimal | |||
| | 2.2360679774997... (≈ 2.236) | |||
| ! In duodecimal | |||
| | 2.29ƐƐ132540589... (≈ 2.2ᘔ) | |||
| |- | |- | ||
| | style="text-align:center;"| ] |
| style="text-align:center;"| {{mvar|]}} (pi), the ratio of a circle's ] to its ] | ||
| | 3.141592653589... | |||
| | 1.6180339887498... (≈ 1.618) | |||
| | 3;184809493{{d3}}91... | |||
| | 1.74ƐƐ6772802ᘔ4... (≈ 1.75) | |||
| |- style="text-align:center;" | |||
| || ''Transcendental irrational number'' | |||
| || In decimal | |||
| || '''In duodecimal''' | |||
| |- | |- | ||
| | style="text-align:center;"| |
| style="text-align:center;"| {{mvar|]}}, the base of the ] | ||
| | 2.718281828459... | |||
| | 3.1415926535897932384626433<br>8327950288419716939937510...<br>(≈ 3.1416) | |||
| | 2;875236069821... | |||
| | 3.184809493Ɛ918664573ᘔ6211Ɛ<br>Ɛ151551ᘔ05729290ᘔ7809ᘔ492...<br>(≈ 3.1848) | |||
| |- | |||
| | style="text-align:center;"| ] <SMALL>(the base of the ])</SMALL> | |||
| | 2.718281828459045... (≈ 2.718) | |||
| | 2.8752360698219Ɛ8... (≈ 2.875) | |||
| |} | |} | ||
| The first few digits of the decimal and duodecimal representation of another important number, the ] (the status of which as a rational or irrational number is not yet known), are: | |||
| {|class="wikitable" | |||
| |- style="text-align:center;" | |||
| || ''Number'' | |||
| || In decimal | |||
| || '''In duodecimal''' | |||
| |- | |||
| | style="text-align:center;"| ] <SMALL>(the limiting difference between the ] and the natural logarithm)</SMALL> | |||
| | 0.57721566490153... (≈ 0.577) | |||
| | 0.6Ɛ15188ᘔ6760Ɛ3... (≈ 0.7) | |||
| |} | |||
| ==Advocacy and "dozenalism"== | |||
| The case for the duodecimal system was put forth at length in F. Emerson Andrews' 1935 book ''New Numbers: How Acceptance of a Duodecimal Base Would Simplify Mathematics''. Emerson noted that, due to the prevalence of factors of twelve in many traditional units of weight and measure, many of the computational advantages claimed for the metric system could be realized ''either'' by the adoption of ten-based weights and measure ''or'' by the adoption of the duodecimal number system. | |||
| Rather than the symbols "A" for ten and "B" for eleven as used in ] notation and ] notation (or "T" and "E" for ten and eleven), he suggested in his book and used a script X and a script E, <math>x\!</math> (]1D4B3) and ] (U+2130), to represent the digits ten and eleven respectively, because, at least on a page of Roman script, these characters were distinct from any existing letters or numerals, yet were readily available in printers' fonts. He chose <math>x\!</math> for its resemblance to the Roman numeral X, and ] as the first letter of the word "eleven". | |||
| Another popular notation, introduced by Sir ], is to use a rotated 2 (ᘔ) (resembling a script ''τ'' for "ten") to represent ten and a rotated or horizontally flipped 3 (Ɛ) to represent eleven. This is the convention commonly employed by the Dozenal Society of Great Britain and has the advantage of being easily recognizable as digits because of their resemblance in shape to existing digits. On the other hand, the Dozenal Society of America adopted for some years the convention of using a ] ⚹ for ten and a ] ⌗ for eleven. The reason was that the symbol ⚹ resembles a struck-through X, whereas the symbol ⌗ resembles a doubly struck-through 11, and both symbols are already present in ] ]. However, critics pointed out these symbols do not look anything like digits. Some other systems write 10 as Φ (a combination of 1 and 0) and eleven as a cross of two lines (+, x, or † for example)<!-- "+" is similar to the Chinese character for ten & "X" is the Roman numeral for ten. -->. | |||
| Problems with these symbols are evident, most notably that most of them cannot be represented in the ] of most ] displays (<math>x\!</math> and ] being an exception, although "E" is used on calculators to indicate an ], and <math>x\!</math> requiring some distortion). However, 10 and 11 do fit, both within a single digit (11 fits as is, whereas the 10 has to be tilted sideways, resulting in a character that resembles an O with a ], ō or <u>o</u>). A and B also fit (although B must be represented as lowercase "b" and as such, 6 must have a bar over it to distinguish the two figures) and are used on calculators for bases higher than ten. | |||
| Other problems relate to the current usage of most of the proposed symbols as variables or quantities in physics and mathematics. Of particular concern to mathematicians is <math>x\!</math> which has ubiquitous usage as an unknown quantity in algebra. | |||
| In "Little Twelvetoes", American television series '']'' portrayed an alien child using base-twelve arithmetic, using "dek", "el" and "doh" as names for ten, eleven and twelve, and Andrews' script-X and script-E for the digit symbols. ("Dek" is from the prefix "deca", "el" being short for "eleven" and "doh" an apparent shortening of "dozen".)<ref> {{wayback|url=http://www.schoolhouserock.tv/Little.html |date=20130618004000 }}</ref> | |||
| ]]] | |||
| The Dozenal Society of America and the Dozenal Society of Great Britain promote widespread adoption of the base-twelve system. They use the word "dozenal" instead of "duodecimal" because the latter comes from Latin roots that express twelve in base-ten terminology. | |||
| The renowned mathematician and mental calculator ] was an outspoken advocate of the advantages and superiority of duodecimal over decimal: | |||
| {{quote|The duodecimal tables are easy to master, easier than the decimal ones; and in elementary teaching they would be so much more interesting, since young children would find more fascinating things to do with twelve rods or blocks than with ten. Anyone having these tables at command will do these calculations more than one-and-a-half times as fast in the duodecimal scale as in the decimal. This is my experience; I am certain that even more so it would be the experience of others.|A. C. Aitken|in ''The Listener'', January 25, 1962<ref>{{dead link|date=January 2014}}</ref>}} | |||
| {{quote|But the final quantitative advantage, in my own experience, is this: in varied and extensive calculations of an ordinary and not unduly complicated kind, carried out over many years, I come to the conclusion that the efficiency of the decimal system might be rated at about 65 or less, if we assign 100 to the duodecimal.|A. C. Aitken|''The Case Against Decimalisation'' (Edinburgh / London: Oliver & Boyd, 1962)<ref></ref>}} | |||
| In ]'s ] novels, Conrad introduces a duodecimal system of arithmetic at the suggestion of a merchant, who is accustomed to buying and selling goods in dozens and grosses, rather than tens or hundreds. He then invents an entire system of weights and measures in base twelve, including a clock with twelve hours in a day, rather than twenty-four hours. | |||
| In ]'s ''Kryon: Alchemy of the Human Spirit'', a chapter is dedicated to the advantages of the duodecimal system. The duodecimal system is supposedly suggested by ] (a fictional entity believed in by ] circles) for all-round use, aiming at better and more natural representation of nature of the Universe through mathematics. An individual article "Mathematica" by James D. Watt (included in the above publication) exposes a few of the unusual symmetry connections between the duodecimal system and the ], as well as provides numerous number symmetry-based arguments for the universal nature of the base-12 number system.<ref>'''', ISBN 0-9636304-8-2</ref> | |||
| === Duodecimal clock === | |||
| * | |||
| * | |||
| === Duodecimal metric systems === | |||
| ] proposed by dozenalists include: | |||
| * ]'s ] system<ref>{{cite web|last=Pendlebury|first=Tom|title=TGM|url=http://www.dozenalsociety.org.uk/pdfs/TGMbooklet.pdf}}</ref> | |||
| * ]'s ]<ref>{{cite web|last=Suga|first=Takashi|title=Universal Unit System|url=http://www.asahi-net.or.jp/~dd6t-sg/univunit-e/}}</ref> | |||
| == Duodecimal digits on computerized writing systems == | |||
| {{Symb|] ]<br>] ]}} | |||
| In March 2013, a proposal was submitted to include the digit forms for ten and eleven propagated by the Dozenal Societies of Great Britain and America in the ].<ref name="N4399">{{cite web |author=Karl Pentzlin |publisher=ISO/IEC JTC1/SC2/WG2, Document N4399 |title=Proposal to encode Duodecimal Digit Forms in the UCS|url=http://std.dkuug.dk/jtc1/sc2/wg2/docs/n4399.pdf |date=2013-03-30 |access-date=2013-06-29|format=PDF |language=en}}</ref> Of these, the British forms were accepted for encoding as characters at code points U+218A {{smallcaps|turned digit two}} ({{unicode|↊}}) and U+218B {{smallcaps|turned digit three}} ({{unicode|↋}}) They have been included in the ] release in June 2015.<ref name="Unicode8">{{Cite web | url=http://unicode.org/versions/Unicode8.0.0/ | title=Unicode 8.0.0 | publisher=Unicode Consortium | accessdate=17 June 2015 }}</ref><ref>{{Cite web | url=http://www.unicode.org/charts/PDF/Unicode-8.0/U80-2150.pdf | title=The Unicode Standard, Version 8.0: Number Forms | publisher=Unicode Consortium | accessdate=8 April 2015 }}</ref> | |||
| Few fonts support these new characters in late 2015, but , ], ], ], and Symbola do. | |||
| Also, the turned digits two and three are available in ] as <code>\textturntwo</code> and <code>\textturnthree</code>.<ref name="LATEX">{{cite web |author = Scott Pakin |title=The Comprehensive LATEX Symbol List | |||
| |url = http://www.tex.ac.uk/tex-archive/info/symbols/comprehensive/symbols-a4.pdf |date=2009-11-09 |access-date=2013-02-04 | |||
| |format = PDF | |||
| |language=German}}</ref> | |||
| == See also == | == See also == | ||
| * ] (base |
* ] (base 20) | ||
| * ] (base 60) | * ] (base 60) | ||
| Line 1,237: | Line 1,167: | ||
| == External links == | == External links == | ||
| * | * | ||
| ** | |||
| * | |||
| ** , the DSA website's page of external links to third-party tools | |||
| * | |||
| * | |||
| * | |||
| * {{cite web|last= |
* {{cite web |last=Lauritzen |first=Bill |year=1994 |title=Nature's Numbers |work=Earth360 |url=http://www.earth360.com/new_number.html }} | ||
| * {{cite web |last=Savard |first=John J. G. |year=2018 |title=Changing the Base |orig-year=2016 |work=quadibloc |url=http://www.quadibloc.com/math/baseint.htm |access-date=2018-07-17 }} | |||
| ] | ] | ||
| ] | |||
Latest revision as of 06:51, 11 January 2025
Base-12 numeral system Not to be confused with Dewey Decimal Classification or Duodecimo.| Part of a series on | ||||
| Numeral systems | ||||
|---|---|---|---|---|
Place-value notation
|
||||
Sign-value notation
|
||||
| List of numeral systems | ||||
The duodecimal system, also known as base twelve or dozenal, is a positional numeral system using twelve as its base. In duodecimal, the number twelve is denoted "10", meaning 1 twelve and 0 units; in the decimal system, this number is instead written as "12" meaning 1 ten and 2 units, and the string "10" means ten. In duodecimal, "100" means twelve squared, "1000" means twelve cubed, and "0.1" means a twelfth.
Various symbols have been used to stand for ten and eleven in duodecimal notation; this page uses A and B, as in hexadecimal, which make a duodecimal count from zero to twelve read 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, 10. The Dozenal Societies of America and Great Britain (organisations promoting the use of duodecimal) use turned digits in their published material: 2 (a turned 2) for ten and 3 (a turned 3) for eleven.
The number twelve, a superior highly composite number, is the smallest number with four non-trivial factors (2, 3, 4, 6), and the smallest to include as factors all four numbers (1 to 4) within the subitizing range, and the smallest abundant number. All multiples of reciprocals of 3-smooth numbers (a/2·3 where a,b,c are integers) have a terminating representation in duodecimal. In particular, +1/4 (0.3), +1/3 (0.4), +1/2 (0.6), +2/3 (0.8), and +3/4 (0.9) all have a short terminating representation in duodecimal. There is also higher regularity observable in the duodecimal multiplication table. As a result, duodecimal has been described as the optimal number system.
In these respects, duodecimal is considered superior to decimal, which has only 2 and 5 as factors, and other proposed bases like octal or hexadecimal. Sexagesimal (base sixty) does even better in this respect (the reciprocals of all 5-smooth numbers terminate), but at the cost of unwieldy multiplication tables and a much larger number of symbols to memorize.
Origin
- In this section, numerals are in decimal. For example, "10" means 9+1, and "12" means 9+3.
Georges Ifrah speculatively traced the origin of the duodecimal system to a system of finger counting based on the knuckle bones of the four larger fingers. Using the thumb as a pointer, it is possible to count to 12 by touching each finger bone, starting with the farthest bone on the fifth finger, and counting on. In this system, one hand counts repeatedly to 12, while the other displays the number of iterations, until five dozens, i.e. the 60, are full. This system is still in use in many regions of Asia.
Languages using duodecimal number systems are uncommon. Languages in the Nigerian Middle Belt such as Janji, Gbiri-Niragu (Gure-Kahugu), Piti, and the Nimbia dialect of Gwandara; and the Chepang language of Nepal are known to use duodecimal numerals.
Germanic languages have special words for 11 and 12, such as eleven and twelve in English. They come from Proto-Germanic *ainlif and *twalif (meaning, respectively, one left and two left), suggesting a decimal rather than duodecimal origin. However, Old Norse used a hybrid decimal–duodecimal counting system, with its words for "one hundred and eighty" meaning 200 and "two hundred" meaning 240. In the British Isles, this style of counting survived well into the Middle Ages as the long hundred.
Historically, units of time in many civilizations are duodecimal. There are twelve signs of the zodiac, twelve months in a year, and the Babylonians had twelve hours in a day (although at some point, this was changed to 24). Traditional Chinese calendars, clocks, and compasses are based on the twelve Earthly Branches or 24 (12×2) Solar terms. There are 12 inches in an imperial foot, 12 troy ounces in a troy pound, 12 old British pence in a shilling, 24 (12×2) hours in a day; many other items are counted by the dozen, gross (144, square of 12), or great gross (1728, cube of 12). The Romans used a fraction system based on 12, including the uncia, which became both the English words ounce and inch. Pre-decimalisation, Ireland and the United Kingdom used a mixed duodecimal-vigesimal currency system (12 pence = 1 shilling, 20 shillings or 240 pence to the pound sterling or Irish pound), and Charlemagne established a monetary system that also had a mixed base of twelve and twenty, the remnants of which persist in many places.
| Relative value |
Length | Weight | ||
|---|---|---|---|---|
| French | English | English (Troy) | Roman | |
| 12 | pied | foot | pound | libra |
| 12 | pouce | inch | ounce | uncia |
| 12 | ligne | line | 2 scruples | 2 scrupula |
| 12 | point | point | seed | siliqua |
Notations and pronunciations
In a positional numeral system of base n (twelve for duodecimal), each of the first n natural numbers is given a distinct numeral symbol, and then n is denoted "10", meaning 1 times n plus 0 units. For duodecimal, the standard numeral symbols for 0–9 are typically preserved for zero through nine, but there are numerous proposals for how to write the numerals representing "ten" and "eleven". More radical proposals do not use any Arabic numerals under the principle of "separate identity."
Pronunciation of duodecimal numbers also has no standard, but various systems have been proposed.
Transdecimal symbols
| 2 3 | |
|---|---|
| duodecimal ⟨ten, eleven⟩ | |
| In Unicode |
|
| Block Number Forms | |
| Note | |
| |
Several authors have proposed using letters of the alphabet for the transdecimal symbols. Latin letters such as ⟨A, B⟩ (as in hexadecimal) or ⟨T, E⟩ (initials of Ten and Eleven) are convenient because they are widely accessible, and for instance can be typed on typewriters. However, when mixed with ordinary prose, they might be confused for letters. As an alternative, Greek letters such as ⟨τ, ε⟩ could be used instead. Frank Emerson Andrews, an early American advocate for duodecimal, suggested and used in his 1935 book New Numbers ⟨X, Ɛ⟩ (italic capital X from the Roman numeral for ten and a rounded italic capital E similar to open E), along with italic numerals 0–9.
Edna Kramer in her 1951 book The Main Stream of Mathematics used a ⟨*, #⟩ (sextile or six-pointed asterisk, hash or octothorpe). The symbols were chosen because they were available on some typewriters; they are also on push-button telephones. This notation was used in publications of the Dozenal Society of America (DSA) from 1974 to 2008.
From 2008 to 2015, the DSA used ⟨ ![]() ,
, ![]() ⟩, the symbols devised by William Addison Dwiggins.
⟩, the symbols devised by William Addison Dwiggins.
The Dozenal Society of Great Britain (DSGB) proposed symbols ⟨ 2, 3 ⟩. This notation, derived from Arabic digits by 180° rotation, was introduced by Isaac Pitman in 1857. In March 2013, a proposal was submitted to include the digit forms for ten and eleven propagated by the Dozenal Societies in the Unicode Standard. Of these, the British/Pitman forms were accepted for encoding as characters at code points U+218A ↊ TURNED DIGIT TWO and U+218B ↋ TURNED DIGIT THREE. They were included in Unicode 8.0 (2015).
After the Pitman digits were added to Unicode, the DSA took a vote and then began publishing PDF content using the Pitman digits instead, but continues to use the letters X and E on its webpage.
| Symbols | Background | Note | |
|---|---|---|---|
| A | B | As in hexadecimal | Allows entry on typewriters. |
| T | E | Initials of Ten and Eleven | Used (in lower case) in music set theory |
| X | E | X from the Roman numeral; E from Eleven. |
|
| X | Z | Origin of Z unknown | Attributed to D'Alembert & Buffon by the DSA. |
| δ | ε | Greek delta from δέκα "ten"; epsilon from ένδεκα "eleven" |
|
| τ | ε | Greek tau, epsilon | |
| W | ∂ | W from doubling the Roman numeral V; ∂ based on a pendulum |
Silvio Ferrari in Calcolo Decidozzinale (1854). |
| X | Ɛ | italic X pronounced "dec"; rounded italic Ɛ, pronounced "elf" |
Frank Andrews in New Numbers (1935), with italic 0–9 for other duodecimal numerals. |
| * | # | sextile or six-pointed asterisk, hash or octothorpe |
On push-button telephones; used by Edna Kramer in The Main Stream of Mathematics (1951); used by the DSA 1974–2008 |
| 2 | 3 |
|
Isaac Pitman (1857); used by the DSGB; used by the DSA since 2015; included in Unicode 8.0 (2015) |
| Pronounced "dek", "el" |
| ||
Base notation
There are also varying proposals of how to distinguish a duodecimal number from a decimal one. The most common method used in mainstream mathematics sources comparing various number bases uses a subscript "10" or "12", e.g. "5412 = 6410". To avoid ambiguity about the meaning of the subscript 10, the subscripts might be spelled out, "54twelve = 64ten". In 2015 the Dozenal Society of America adopted the more compact single-letter abbreviation "z" for "dozenal" and "d" for "decimal", "54z = 64d".
Other proposed methods include italicizing duodecimal numbers "54 = 64", adding a "Humphrey point" (a semicolon instead of a decimal point) to duodecimal numbers "54;6 = 64.5", prefixing duodecimal numbers by an asterisk "*54 = 64", or some combination of these. The Dozenal Society of Great Britain uses an asterisk prefix for duodecimal whole numbers, and a Humphrey point for other duodecimal numbers.
Pronunciation
The Dozenal Society of America suggested the pronunciation of ten and eleven as "dek" and "el". For the names of powers of twelve, there are two prominent systems. In spite of the efficiency of these newer systems, terms for powers of twelve either already exist or remain easily reconstructed in English using words and affixes.
Base-12 nomenclature in English
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (November 2024) (Learn how and when to remove this message) |
Another nominal for twelve (1210) is a dozen (1012 or 1•1012).
One hundred and forty-four (14410) is also known as a gross (10012 or 1•1012).
One thousand, seven hundred and twenty-eight is (172810) also known as a great-gross (1,00012 or 1•1012).
For the next powers of twelve that follow those aforementioned, the affixes (dozen-, gross-, great-) are used to produce names for these powers of twelve that have a greater positional-notation value. 20,73610 or 10,00012 may be rendered a dozen-great-gross; so 248,83210 or 100,00012 is a gross-great-gross, with 2,985,98410 or 1,000,00012 being known as a great-great-gross.
It should be made plain that the indice's being a multiple of three, e.g. 1012 , 1012 , 1012 results, in these examples, in a great gross, a great-great-gross, and a great-great-great-gross, respectively.
| Scientific notation | Positional notation | Name | Decimal |
|---|---|---|---|
| 1•10 | 1 | One | 1 |
| A•10 | A | Ten | 10 |
| B•10 | B | Eleven | 11 |
| 1•10 | 10 | Twelve | 12 |
| 5•10 | 50 | Five dozen | 60 |
| 1•10 | 100 | One gross | 144 |
| 2;6•10 | 260 | Two gross, six dozen | 360 |
| 1•10 | 1,000 | One great-gross | 1,728 |
| 1•10 | 10,000 | One dozen-great-gross | 20,736 |
| 1•10 | 100,000 | One gross-great-gross | 248,832 |
| 1•10 | 1,000,000 | One great-great-gross | 2,985,984 |
Duodecimal numbers
In this system, the prefix e- is added for fractions.
| Duodecimal number |
Number name |
Decimal number |
Duodecimal fraction |
Fraction name |
|---|---|---|---|---|
| 1; | one | 1 | ||
| 10; | do | 12 | 0;1 | edo |
| 100; | gro | 144 | 0;01 | egro |
| 1,000; | mo | 1,728 | 0;001 | emo |
| 10,000; | do-mo | 20,736 | 0;000,1 | edo-mo |
| 100,000; | gro-mo | 248,832 | 0;000,01 | egro-mo |
| 1,000,000; | bi-mo | 2,985,984 | 0;000,001 | ebi-mo |
| 10,000,000; | do-bi-mo | 35,831,808 | 0;000,000,1 | edo-bi-mo |
| 100,000,000; | gro-bi-mo | 429,981,696 | 0;000,000,01 | egro-bi-mo |
As numbers get larger (or fractions smaller), the last two morphemes are successively replaced with tri-mo, quad-mo, penta-mo, and so on.
Multiple digits in this series are pronounced differently: 12 is "do two"; 30 is "three do"; 100 is "gro"; BA9 is "el gro dek do nine"; B86 is "el gro eight do six"; 8BB,15A is "eight gro el do el, one gro five do dek"; ABA is "dek gro el do dek"; BBB is "el gro el do el"; 0.06 is "six egro"; and so on.
Systematic Dozenal Nomenclature (SDN)
This system uses "-qua" ending for the positive powers of 12 and "-cia" ending for the negative powers of 12, and an extension of the IUPAC systematic element names (with syllables dec and lev for the two extra digits needed for duodecimal) to express which power is meant.
| Duodecimal number |
Number name |
Decimal number |
Duodecimal fraction |
Fraction name |
|---|---|---|---|---|
| 1; | one | 1 | ||
| 10; | unqua | 12 | 0;1 | uncia |
| 100; | biqua | 144 | 0;01 | bicia |
| 1,000; | triqua | 1,728 | 0;001 | tricia |
| 10,000; | quadqua | 20,736 | 0;000,1 | quadcia |
| 100,000; | pentqua | 248,832 | 0;000,01 | pentcia |
| 1,000,000; | hexqua | 2,985,984 | 0;000,001 | hexcia |
After hex-, further prefixes continue sept-, oct-, enn-, dec-, lev-, unnil-, unun-.
Advocacy and "dozenalism"
William James Sidis used 12 as the base for his constructed language Vendergood in 1906, noting it being the smallest number with four factors and its prevalence in commerce.
The case for the duodecimal system was put forth at length in Frank Emerson Andrews' 1935 book New Numbers: How Acceptance of a Duodecimal Base Would Simplify Mathematics. Emerson noted that, due to the prevalence of factors of twelve in many traditional units of weight and measure, many of the computational advantages claimed for the metric system could be realized either by the adoption of ten-based weights and measure or by the adoption of the duodecimal number system.
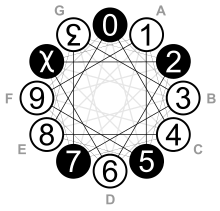
Both the Dozenal Society of America and the Dozenal Society of Great Britain promote widespread adoption of the duodecimal system. They use the word "dozenal" instead of "duodecimal" to avoid the more overtly decimal terminology. However, the etymology of "dozenal" itself is also an expression based on decimal terminology since "dozen" is a direct derivation of the French word douzaine, which is a derivative of the French word for twelve, douze, descended from Latin duodecim.
Mathematician and mental calculator Alexander Craig Aitken was an outspoken advocate of duodecimal:
The duodecimal tables are easy to master, easier than the decimal ones; and in elementary teaching they would be so much more interesting, since young children would find more fascinating things to do with twelve rods or blocks than with ten. Anyone having these tables at command will do these calculations more than one-and-a-half times as fast in the duodecimal scale as in the decimal. This is my experience; I am certain that even more so it would be the experience of others.
— A. C. Aitken, "Twelves and Tens" in The Listener (January 25, 1962)
But the final quantitative advantage, in my own experience, is this: in varied and extensive calculations of an ordinary and not unduly complicated kind, carried out over many years, I come to the conclusion that the efficiency of the decimal system might be rated at about 65 or less, if we assign 100 to the duodecimal.
— A. C. Aitken, The Case Against Decimalisation (1962)
In media
In "Little Twelvetoes," an episode of the American educational television series Schoolhouse Rock!, a farmer encounters an alien being with twelve fingers on each hand and twelve toes on each foot who uses duodecimal arithmetic. The alien uses "dek" and "el" as names for ten and eleven, and Andrews' script-X and script-E for the digit symbols.
Duodecimal systems of measurements
Systems of measurement proposed by dozenalists include:
- Tom Pendlebury's TGM system
- Takashi Suga's Universal Unit System
- John Volan's Primel system
Comparison to other number systems
- In this section, numerals are in decimal. For example, "10" means 9+1, and "12" means 9+3.
The Dozenal Society of America argues that if a base is too small, significantly longer expansions are needed for numbers; if a base is too large, one must memorise a large multiplication table to perform arithmetic. Thus, it presumes that "a number base will need to be between about 7 or 8 through about 16, possibly including 18 and 20".
The number 12 has six factors, which are 1, 2, 3, 4, 6, and 12, of which 2 and 3 are prime. It is the smallest number to have six factors, the largest number to have at least half of the numbers below it as divisors, and is only slightly larger than 10. (The numbers 18 and 20 also have six factors but are much larger.) Ten, in contrast, only has four factors, which are 1, 2, 5, and 10, of which 2 and 5 are prime. Six shares the prime factors 2 and 3 with twelve; however, like ten, six only has four factors (1, 2, 3, and 6) instead of six. Its corresponding base, senary, is below the DSA's stated threshold.
Eight and sixteen only have 2 as a prime factor. Therefore, in octal and hexadecimal, the only terminating fractions are those whose denominator is a power of two.
Thirty is the smallest number that has three different prime factors (2, 3, and 5, the first three primes), and it has eight factors in total (1, 2, 3, 5, 6, 10, 15, and 30). Sexagesimal was actually used by the ancient Sumerians and Babylonians, among others; its base, sixty, adds the four convenient factors 4, 12, 20, and 60 to 30 but no new prime factors. The smallest number that has four different prime factors is 210; the pattern follows the primorials. However, these numbers are quite large to use as bases, and are far beyond the DSA's stated threshold.
In all base systems, there are similarities to the representation of multiples of numbers that are one less than or one more than the base.
In the following multiplication table, numerals are written in duodecimal. For example, "10" means twelve, and "12" means fourteen.
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | 10 |
| 2 | 2 | 4 | 6 | 8 | A | 10 | 12 | 14 | 16 | 18 | 1A | 20 |
| 3 | 3 | 6 | 9 | 10 | 13 | 16 | 19 | 20 | 23 | 26 | 29 | 30 |
| 4 | 4 | 8 | 10 | 14 | 18 | 20 | 24 | 28 | 30 | 34 | 38 | 40 |
| 5 | 5 | A | 13 | 18 | 21 | 26 | 2B | 34 | 39 | 42 | 47 | 50 |
| 6 | 6 | 10 | 16 | 20 | 26 | 30 | 36 | 40 | 46 | 50 | 56 | 60 |
| 7 | 7 | 12 | 19 | 24 | 2B | 36 | 41 | 48 | 53 | 5A | 65 | 70 |
| 8 | 8 | 14 | 20 | 28 | 34 | 40 | 48 | 54 | 60 | 68 | 74 | 80 |
| 9 | 9 | 16 | 23 | 30 | 39 | 46 | 53 | 60 | 69 | 76 | 83 | 90 |
| A | A | 18 | 26 | 34 | 42 | 50 | 5A | 68 | 76 | 84 | 92 | A0 |
| B | B | 1A | 29 | 38 | 47 | 56 | 65 | 74 | 83 | 92 | A1 | B0 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | A0 | B0 | 100 |
Conversion tables to and from decimal
To convert numbers between bases, one can use the general conversion algorithm (see the relevant section under positional notation). Alternatively, one can use digit-conversion tables. The ones provided below can be used to convert any duodecimal number between 0;1 and BB,BBB;B to decimal, or any decimal number between 0.1 and 99,999.9 to duodecimal. To use them, the given number must first be decomposed into a sum of numbers with only one significant digit each. For example:
- 12,345.6 = 10,000 + 2,000 + 300 + 40 + 5 + 0.6
This decomposition works the same no matter what base the number is expressed in. Just isolate each non-zero digit, padding them with as many zeros as necessary to preserve their respective place values. If the digits in the given number include zeroes (for example, 7,080.9), these are left out in the digit decomposition (7,080.9 = 7,000 + 80 + 0.9). Then, the digit conversion tables can be used to obtain the equivalent value in the target base for each digit. If the given number is in duodecimal and the target base is decimal, we get:
- (duodecimal) 10,000 + 2,000 + 300 + 40 + 5 + 0;6
= (decimal) 20,736 + 3,456 + 432 + 48 + 5 + 0.5
Because the summands are already converted to decimal, the usual decimal arithmetic is used to perform the addition and recompose the number, arriving at the conversion result:
Duodecimal ---> Decimal
10,000 = 20,736
2,000 = 3,456
300 = 432
40 = 48
5 = 5
+ 0;6 = + 0.5
-----------------------------
12,345;6 = 24,677.5
That is, (duodecimal) 12,345;6 equals (decimal) 24,677.5
If the given number is in decimal and the target base is duodecimal, the method is same. Using the digit conversion tables:
(decimal) 10,000 + 2,000 + 300 + 40 + 5 + 0.6
= (duodecimal) 5,954 + 1,1A8 + 210 + 34 + 5 + 0;7249
To sum these partial products and recompose the number, the addition must be done with duodecimal rather than decimal arithmetic:
Decimal --> Duodecimal
10,000 = 5,954
2,000 = 1,1A8
300 = 210
40 = 34
5 = 5
+ 0.6 = + 0;7249
-------------------------------
12,345.6 = 7,189;7249
That is, (decimal) 12,345.6 equals (duodecimal) 7,189;7249
Duodecimal to decimal digit conversion
| Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10,000 | 20,736 | 1,000 | 1,728 | 100 | 144 | 10 | 12 | 1 | 1 | 0;1 | 0.083 |
| 20,000 | 41,472 | 2,000 | 3,456 | 200 | 288 | 20 | 24 | 2 | 2 | 0;2 | 0.16 |
| 30,000 | 62,208 | 3,000 | 5,184 | 300 | 432 | 30 | 36 | 3 | 3 | 0;3 | 0.25 |
| 40,000 | 82,944 | 4,000 | 6,912 | 400 | 576 | 40 | 48 | 4 | 4 | 0;4 | 0.3 |
| 50,000 | 103,680 | 5,000 | 8,640 | 500 | 720 | 50 | 60 | 5 | 5 | 0;5 | 0.416 |
| 60,000 | 124,416 | 6,000 | 10,368 | 600 | 864 | 60 | 72 | 6 | 6 | 0;6 | 0.5 |
| 70,000 | 145,152 | 7,000 | 12,096 | 700 | 1,008 | 70 | 84 | 7 | 7 | 0;7 | 0.583 |
| 80,000 | 165,888 | 8,000 | 13,824 | 800 | 1,152 | 80 | 96 | 8 | 8 | 0;8 | 0.6 |
| 90,000 | 186,624 | 9,000 | 15,552 | 900 | 1,296 | 90 | 108 | 9 | 9 | 0;9 | 0.75 |
| A0,000 | 207,360 | A,000 | 17,280 | A00 | 1,440 | A0 | 120 | A | 10 | 0;A | 0.83 |
| B0,000 | 228,096 | B,000 | 19,008 | B00 | 1,584 | B0 | 132 | B | 11 | 0;B | 0.916 |
Decimal to duodecimal digit conversion
| Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duodecimal |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10,000 | 5,954 | 1,000 | 6B4 | 100 | 84 | 10 | A | 1 | 1 | 0.1 | 0;12497 |
| 20,000 | B,6A8 | 2,000 | 1,1A8 | 200 | 148 | 20 | 18 | 2 | 2 | 0.2 | 0;2497 |
| 30,000 | 15,440 | 3,000 | 1,8A0 | 300 | 210 | 30 | 26 | 3 | 3 | 0.3 | 0;37249 |
| 40,000 | 1B,194 | 4,000 | 2,394 | 400 | 294 | 40 | 34 | 4 | 4 | 0.4 | 0;4972 |
| 50,000 | 24,B28 | 5,000 | 2,A88 | 500 | 358 | 50 | 42 | 5 | 5 | 0.5 | 0;6 |
| 60,000 | 2A,880 | 6,000 | 3,580 | 600 | 420 | 60 | 50 | 6 | 6 | 0.6 | 0;7249 |
| 70,000 | 34,614 | 7,000 | 4,074 | 700 | 4A4 | 70 | 5A | 7 | 7 | 0.7 | 0;84972 |
| 80,000 | 3A,368 | 8,000 | 4,768 | 800 | 568 | 80 | 68 | 8 | 8 | 0.8 | 0;9724 |
| 90,000 | 44,100 | 9,000 | 5,260 | 900 | 630 | 90 | 76 | 9 | 9 | 0.9 | 0;A9724 |
Fractions and irrational numbers
Fractions
Duodecimal fractions for rational numbers with 3-smooth denominators terminate:
- 1/2 = 0;6
- 1/3 = 0;4
- 1/4 = 0;3
- 1/6 = 0;2
- 1/8 = 0;16
- 1/9 = 0;14
- 1/10 = 0;1 (this is one twelfth, 1/A is one tenth)
- 1/14 = 0;09 (this is one sixteenth, 1/12 is one fourteenth)
while other rational numbers have recurring duodecimal fractions:
- 1/5 = 0;2497
- 1/7 = 0;186A35
- 1/A = 0;12497 (one tenth)
- 1/B = 0;1 (one eleventh)
- 1/11 = 0;0B (one thirteenth)
- 1/12 = 0;0A35186 (one fourteenth)
- 1/13 = 0;09724 (one fifteenth)
| Examples in duodecimal | Decimal equivalent |
|---|---|
| 1 × 5/8 = 0.76 | 1 × 5/8 = 0.625 |
| 100 × 5/8 = 76 | 144 × 5/8 = 90 |
| 576/9 = 76 | 810/9 = 90 |
| 400/9 = 54 | 576/9 = 64 |
| 1A.6 + 7.6 = 26 | 22.5 + 7.5 = 30 |
As explained in recurring decimals, whenever an irreducible fraction is written in radix point notation in any base, the fraction can be expressed exactly (terminates) if and only if all the prime factors of its denominator are also prime factors of the base.
Because in the decimal system, fractions whose denominators are made up solely of multiples of 2 and 5 terminate: 1/8 = 1/(2×2×2), 1/20 = 1/(2×2×5), and 1/500 = 1/(2×2×5×5×5) can be expressed exactly as 0.125, 0.05, and 0.002 respectively. 1/3 and 1/7, however, recur (0.333... and 0.142857142857...).
Because in the duodecimal system, 1/8 is exact; 1/20 and 1/500 recur because they include 5 as a factor; 1/3 is exact, and 1/7 recurs, just as it does in decimal.
The number of denominators that give terminating fractions within a given number of digits, n, in a base b is the number of factors (divisors) of , the nth power of the base b (although this includes the divisor 1, which does not produce fractions when used as the denominator). The number of factors of is given using its prime factorization.
For decimal, . The number of divisors is found by adding one to each exponent of each prime and multiplying the resulting quantities together, so the number of factors of is .
For example, the number 8 is a factor of 10 (1000), so and other fractions with a denominator of 8 cannot require more than three fractional decimal digits to terminate.
For duodecimal, . This has divisors. The sample denominator of 8 is a factor of a gross (in decimal), so eighths cannot need more than two duodecimal fractional places to terminate.
Because both ten and twelve have two unique prime factors, the number of divisors of for b = 10 or 12 grows quadratically with the exponent n (in other words, of the order of ).
Recurring digits
The Dozenal Society of America argues that factors of 3 are more commonly encountered in real-life division problems than factors of 5. Thus, in practical applications, the nuisance of repeating decimals is encountered less often when duodecimal notation is used. Advocates of duodecimal systems argue that this is particularly true of financial calculations, in which the twelve months of the year often enter into calculations.
However, when recurring fractions do occur in duodecimal notation, they are less likely to have a very short period than in decimal notation, because 12 (twelve) is between two prime numbers, 11 (eleven) and 13 (thirteen), whereas ten is adjacent to the composite number 9. Nonetheless, having a shorter or longer period does not help the main inconvenience that one does not get a finite representation for such fractions in the given base (so rounding, which introduces inexactitude, is necessary to handle them in calculations), and overall one is more likely to have to deal with infinite recurring digits when fractions are expressed in decimal than in duodecimal, because one out of every three consecutive numbers contains the prime factor 3 in its factorization, whereas only one out of every five contains the prime factor 5. All other prime factors, except 2, are not shared by either ten or twelve, so they do not influence the relative likeliness of encountering recurring digits (any irreducible fraction that contains any of these other factors in its denominator will recur in either base).
Also, the prime factor 2 appears twice in the factorization of twelve, whereas only once in the factorization of ten; which means that most fractions whose denominators are powers of two will have a shorter, more convenient terminating representation in duodecimal than in decimal:
- 1/(2) = 0.2510 = 0.312
- 1/(2) = 0.12510 = 0.1612
- 1/(2) = 0.062510 = 0.0912
- 1/(2) = 0.0312510 = 0.04612
| Decimal base Prime factors of the base: 2, 5 Prime factors of one below the base: 3 Prime factors of one above the base: 11 All other primes: 7, 13, 17, 19, 23, 29, 31 |
Duodecimal base Prime factors of the base: 2, 3 Prime factors of one below the base: B Prime factors of one above the base: 11 (=1310) All other primes: 5, 7, 15 (=1710), 17 (=1910), 1B (=2310), 25 (=2910), 27 (=3110) | ||||
| Fraction | Prime factors of the denominator |
Positional representation | Positional representation | Prime factors of the denominator |
Fraction |
|---|---|---|---|---|---|
| 1/2 | 2 | 0.5 | 0;6 | 2 | 1/2 |
| 1/3 | 3 | 0.3 | 0;4 | 3 | 1/3 |
| 1/4 | 2 | 0.25 | 0;3 | 2 | 1/4 |
| 1/5 | 5 | 0.2 | 0;2497 | 5 | 1/5 |
| 1/6 | 2, 3 | 0.16 | 0;2 | 2, 3 | 1/6 |
| 1/7 | 7 | 0.142857 | 0;186A35 | 7 | 1/7 |
| 1/8 | 2 | 0.125 | 0;16 | 2 | 1/8 |
| 1/9 | 3 | 0.1 | 0;14 | 3 | 1/9 |
| 1/10 | 2, 5 | 0.1 | 0;12497 | 2, 5 | 1/A |
| 1/11 | 11 | 0.09 | 0;1 | B | 1/B |
| 1/12 | 2, 3 | 0.083 | 0;1 | 2, 3 | 1/10 |
| 1/13 | 13 | 0.076923 | 0;0B | 11 | 1/11 |
| 1/14 | 2, 7 | 0.0714285 | 0;0A35186 | 2, 7 | 1/12 |
| 1/15 | 3, 5 | 0.06 | 0;09724 | 3, 5 | 1/13 |
| 1/16 | 2 | 0.0625 | 0;09 | 2 | 1/14 |
| 1/17 | 17 | 0.0588235294117647 | 0;08579214B36429A7 | 15 | 1/15 |
| 1/18 | 2, 3 | 0.05 | 0;08 | 2, 3 | 1/16 |
| 1/19 | 19 | 0.052631578947368421 | 0;076B45 | 17 | 1/17 |
| 1/20 | 2, 5 | 0.05 | 0;07249 | 2, 5 | 1/18 |
| 1/21 | 3, 7 | 0.047619 | 0;06A3518 | 3, 7 | 1/19 |
| 1/22 | 2, 11 | 0.045 | 0;06 | 2, B | 1/1A |
| 1/23 | 23 | 0.0434782608695652173913 | 0;06316948421 | 1B | 1/1B |
| 1/24 | 2, 3 | 0.0416 | 0;06 | 2, 3 | 1/20 |
| 1/25 | 5 | 0.04 | 0;05915343A0B62A68781B | 5 | 1/21 |
| 1/26 | 2, 13 | 0.0384615 | 0;056 | 2, 11 | 1/22 |
| 1/27 | 3 | 0.037 | 0;054 | 3 | 1/23 |
| 1/28 | 2, 7 | 0.03571428 | 0;05186A3 | 2, 7 | 1/24 |
| 1/29 | 29 | 0.0344827586206896551724137931 | 0;04B7 | 25 | 1/25 |
| 1/30 | 2, 3, 5 | 0.03 | 0;04972 | 2, 3, 5 | 1/26 |
| 1/31 | 31 | 0.032258064516129 | 0;0478AA093598166B74311B28623A55 | 27 | 1/27 |
| 1/32 | 2 | 0.03125 | 0;046 | 2 | 1/28 |
| 1/33 | 3, 11 | 0.03 | 0;04 | 3, B | 1/29 |
| 1/34 | 2, 17 | 0.02941176470588235 | 0;0429A708579214B36 | 2, 15 | 1/2A |
| 1/35 | 5, 7 | 0.0285714 | 0;0414559B3931 | 5, 7 | 1/2B |
| 1/36 | 2, 3 | 0.027 | 0;04 | 2, 3 | 1/30 |
The duodecimal period length of 1/n are (in decimal)
- 0, 0, 0, 0, 4, 0, 6, 0, 0, 4, 1, 0, 2, 6, 4, 0, 16, 0, 6, 4, 6, 1, 11, 0, 20, 2, 0, 6, 4, 4, 30, 0, 1, 16, 12, 0, 9, 6, 2, 4, 40, 6, 42, 1, 4, 11, 23, 0, 42, 20, 16, 2, 52, 0, 4, 6, 6, 4, 29, 4, 15, 30, 6, 0, 4, 1, 66, 16, 11, 12, 35, 0, ... (sequence A246004 in the OEIS)
The duodecimal period length of 1/(nth prime) are (in decimal)
- 0, 0, 4, 6, 1, 2, 16, 6, 11, 4, 30, 9, 40, 42, 23, 52, 29, 15, 66, 35, 36, 26, 41, 8, 16, 100, 102, 53, 54, 112, 126, 65, 136, 138, 148, 150, 3, 162, 83, 172, 89, 90, 95, 24, 196, 66, 14, 222, 113, 114, 8, 119, 120, 125, 256, 131, 268, 54, 138, 280, ... (sequence A246489 in the OEIS)
Smallest prime with duodecimal period n are (in decimal)
- 11, 13, 157, 5, 22621, 7, 659, 89, 37, 19141, 23, 20593, 477517, 211, 61, 17, 2693651, 1657, 29043636306420266077, 85403261, 8177824843189, 57154490053, 47, 193, 303551, 79, 306829, 673, 59, 31, 373, 153953, 886381, 2551, 71, 73, ... (sequence A252170 in the OEIS)
Irrational numbers
The representations of irrational numbers in any positional number system (including decimal and duodecimal) neither terminate nor repeat. The following table gives the first digits for some important algebraic and transcendental numbers in both decimal and duodecimal.
| Algebraic irrational number | In decimal | In duodecimal |
|---|---|---|
| √2, the square root of 2 | 1.414213562373... | 1;4B79170A07B8... |
| φ (phi), the golden ratio = | 1.618033988749... | 1;74BB6772802A... |
| Transcendental number | In decimal | In duodecimal |
| π (pi), the ratio of a circle's circumference to its diameter | 3.141592653589... | 3;184809493B91... |
| e, the base of the natural logarithm | 2.718281828459... | 2;875236069821... |
See also
- Vigesimal (base 20)
- Sexagesimal (base 60)
References
- Dvorsky, George (January 18, 2013). "Why We Should Switch To A Base-12 Counting System". Gizmodo. Retrieved December 21, 2013.
- Pittman, Richard (1990). "Origin of Mesopotamian duodecimal and sexagesimal counting systems". Philippine Journal of Linguistics. 21 (1): 97.
- Ifrah, Georges (2000) . The Universal History of Numbers: From prehistory to the invention of the computer. Wiley. ISBN 0-471-39340-1. Translated from the French by David Bellos, E. F. Harding, Sophie Wood and Ian Monk.
- Matsushita, Shuji (October 1998). "Decimal vs. Duodecimal: An interaction between two systems of numeration". www3.aa.tufs.ac.jp. Archived from the original on October 5, 2008. Retrieved May 29, 2011.
- Mazaudon, Martine (2002). "Les principes de construction du nombre dans les langues tibéto-birmanes". In François, Jacques (ed.). La Pluralité (PDF). Leuven: Peeters. pp. 91–119. ISBN 90-429-1295-2. Archived from the original (PDF) on 2016-03-28. Retrieved 2014-03-27.
- von Mengden, Ferdinand (2006). "The peculiarities of the Old English numeral system". In Nikolaus Ritt; Herbert Schendl; Christiane Dalton-Puffer; Dieter Kastovsky (eds.). Medieval English and its Heritage: Structure Meaning and Mechanisms of Change. Studies in English Medieval Language and Literature. Vol. 16. Frankfurt: Peter Lang. pp. 125–145.
- von Mengden, Ferdinand (2010). Cardinal Numerals: Old English from a Cross-Linguistic Perspective. Topics in English Linguistics. Vol. 67. Berlin; New York: De Gruyter Mouton. pp. 159–161.
- Gordon, E V (1957). Introduction to Old Norse. Oxford: Clarendon Press. pp. 292–293.
- ^ De Vlieger, Michael (2010). "Symbology Overview" (PDF). The Duodecimal Bulletin. 4X (2).
- Pakin, Scott (2021) . "The Comprehensive LATEX Symbol List". Comprehensive TEX Archive Network (14.0 ed.). Rei, Fukui (2004) . "tipa – Fonts and macros for IPA phonetics characters". Comprehensive TEX Archive Network (1.3 ed.). The turned digits 2 and 3 employed in the TIPA package originated in The Principles of the International Phonetic Association, University College London, 1949.
- ^ Andrews, Frank Emerson (1935). New Numbers: How Acceptance of a Duodecimal (12) Base Would Simplify Mathematics. Harcourt, Brace and company. p. 52.
- "Annual Meeting of 1973 and Meeting of the Board" (PDF). The Duodecimal Bulletin. 25 (1). 1974.
- De Vlieger, Michael (2008). "Going Classic" (PDF). The Duodecimal Bulletin. 49 (2).
- ^ "Mo for Megro" (PDF). The Duodecimal Bulletin. 1 (1). 1945.
- ^ Pitman, Isaac (24 November 1857). "A Reckoning Reform". Bedfordshire Independent. Reprinted as "Sir Isaac Pitman on the Dozen System: A Reckoning Reform" (PDF). The Duodecimal Bulletin. 3 (2): 1–5. 1947.
- Pentzlin, Karl (March 30, 2013). "Proposal to encode Duodecimal Digit Forms in the UCS" (PDF). ISO/IEC JTC1/SC2/WG2. Retrieved 2024-06-25.
- ^ "The Unicode Standard, Version 8.0: Number Forms" (PDF). Unicode Consortium. Retrieved 2016-05-30.
- "The Unicode Standard 8.0" (PDF). Retrieved 2014-07-18.
- The Dozenal Society of America (n.d.). "What should the DSA do about transdecimal characters?". Dozenal Society of America. The Dozenal Society of America. Retrieved January 1, 2018.
- Arnold Whittall, The Cambridge Introduction to Serialism (New York: Cambridge University Press, 2008): 276. ISBN 978-0-521-68200-8 (pbk).
- Ferrari, Silvio (1854). Calcolo Decidozzinale. p. 2.
- ^ "Annual Meeting of 1973 and Meeting of the Board" (PDF). The Duodecimal Bulletin. 25 (1). 1974.
- ^ De Vlieger, Michael (2008). "Going Classic" (PDF). The Duodecimal Bulletin. 49 (2).
- "The Unicode Standard 8.0" (PDF). Retrieved 2014-07-18.
- ^ Volan, John (July 2015). "Base Annotation Schemes" (PDF). The Duodecimal Bulletin. 62.
- ^ Zirkel, Gene (2010). "How Do You Pronounce Dozenals?" (PDF). The Duodecimal Bulletin. 4E (2).
- "Systematic Dozenal Nomenclature and other nomenclature system" (PDF). The Duodecimal Bulletin. 61 (1).
- ^ Goodman, Donald (2016). "Manual of the Dozenal System" (PDF). Dozenal Society of America. Retrieved 27 April 2018.
- The Prodigy (Biography of WJS) pg
- A. C. Aitken (January 25, 1962) "Twelves and Tens" The Listener.
- A. C. Aitken (1962) The Case Against Decimalisation. Edinburgh / London: Oliver & Boyd.
- "SchoolhouseRock - Little Twelvetoes". 6 February 2010. Archived from the original on 6 February 2010.
- Bellos, Alex (2011-04-04). Alex's Adventures in Numberland. A&C Black. p. 50. ISBN 978-1-4088-0959-4.
- Pendlebury, Tom; Goodman, Donald (2012). "TGM: A Coherent Dozenal Metrology" (PDF). The Dozenal Society of Great Britain.
- Suga, Takashi (22 May 2019). "Proposal for the Universal Unit System" (PDF).
- Volan, John. "The Primel Metrology" (PDF). The Duodecimal Bulletin. 63 (1): 38–60.
- ^ De Vlieger, Michael Thomas (30 November 2011). "Dozenal FAQs" (PDF). dozenal.org. The Dozenal Society of America. Retrieved November 20, 2022.
External links
- Dozenal Society of America
- "The DSA Symbology Synopsis"
- "Resources", the DSA website's page of external links to third-party tools
- Dozenal Society of Great Britain
- Lauritzen, Bill (1994). "Nature's Numbers". Earth360.
- Savard, John J. G. (2018) . "Changing the Base". quadibloc. Retrieved 2018-07-17.
 in the decimal system, fractions whose denominators are made up solely of multiples of 2 and 5 terminate: 1/8 = 1/(2×2×2), 1/20 = 1/(2×2×5), and 1/500 = 1/(2×2×5×5×5) can be expressed exactly as 0.125, 0.05, and 0.002 respectively. 1/3 and 1/7, however, recur (0.333... and 0.142857142857...).
in the decimal system, fractions whose denominators are made up solely of multiples of 2 and 5 terminate: 1/8 = 1/(2×2×2), 1/20 = 1/(2×2×5), and 1/500 = 1/(2×2×5×5×5) can be expressed exactly as 0.125, 0.05, and 0.002 respectively. 1/3 and 1/7, however, recur (0.333... and 0.142857142857...).
 in the duodecimal system, 1/8 is exact; 1/20 and 1/500 recur because they include 5 as a factor; 1/3 is exact, and 1/7 recurs, just as it does in decimal.
in the duodecimal system, 1/8 is exact; 1/20 and 1/500 recur because they include 5 as a factor; 1/3 is exact, and 1/7 recurs, just as it does in decimal.
 , the nth power of the base b (although this includes the divisor 1, which does not produce fractions when used as the denominator). The number of factors of
, the nth power of the base b (although this includes the divisor 1, which does not produce fractions when used as the denominator). The number of factors of  . The number of divisors is found by adding one to each exponent of each prime and multiplying the resulting quantities together, so the number of factors of
. The number of divisors is found by adding one to each exponent of each prime and multiplying the resulting quantities together, so the number of factors of  is
is  .
.
 and other fractions with a denominator of 8 cannot require more than three fractional decimal digits to terminate.
and other fractions with a denominator of 8 cannot require more than three fractional decimal digits to terminate. 
 . This has
. This has  divisors. The sample denominator of 8 is a factor of a gross
divisors. The sample denominator of 8 is a factor of a gross  (in decimal), so eighths cannot need more than two duodecimal fractional places to terminate.
(in decimal), so eighths cannot need more than two duodecimal fractional places to terminate. 
 ).
).
