| Revision as of 20:30, 19 February 2017 editRolf h nelson (talk | contribs)Extended confirmed users6,929 edits →Finite continuous solenoid: rm fact-check template after fixing; feel free to replace if still broken← Previous edit | Latest revision as of 13:03, 18 December 2024 edit undoCitation bot (talk | contribs)Bots5,420,824 edits Altered template type. | Use this bot. Report bugs. | Suggested by Dominic3203 | Category:Actuators | #UCB_Category 9/42 | ||
| (281 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Type of electromagnet formed by a coil of wire}} | |||
| {{Other uses|Solenoid (disambiguation)}} | |||
| {{about|the electromagnet|the device that converts electricity to mechanical energy|solenoid (engineering)|other uses}} | |||
| ] | |||
| ] created by a seven-loop solenoid (cross-sectional view) described using ]s |
] | ||
| ] created by a seven-loop solenoid (cross-sectional view) described using ]s]] | |||
| ]]] | |||
| A '''solenoid''' ( |
A '''solenoid''' ({{IPAc-en|ˈ|s|oʊ|l|ə|n|ɔɪ|d}}<ref>{{cite news |title=solenoid: Meaning in the Cambridge English Dictionary |url=https://dictionary.cambridge.org/dictionary/english/solenoid |website=dictionary.cambridge.org |access-date=16 January 2017 |url-status=live |archive-url=https://web.archive.org/web/20170116173524/https://dictionary.cambridge.org/dictionary/english/solenoid |archive-date=16 January 2017 }}</ref>) is a type of ] formed by a ] coil of ] whose length is substantially greater than its diameter,<ref>or equivalently, the diameter of the coil is assumed to be infinitesimally small (Ampère 1823, p. 267: "des courants électriques formants de très-petits circuits autour de cette ligne, dans des plans infiniment rapprochés qui lui soient perpendiculaires").</ref> which generates a controlled ]. The coil can produce a uniform magnetic field in a volume of space when an ] is passed through it. | ||
| ] coined the term ''solenoid'' in 1823, having conceived of the device in 1820.<ref>Session of the '']'' of 22 December 1823, published in print in: Ampère, "Mémoire sur la théorie mathématique des phénomènes électro-dynamiques", ''Mémoires de l'Académie royale des sciences de l'Institut de France'' 6 (1827), Paris, F. Didot, (and ). "l'assemblage de tous les circuits qui l'entourent , assemblage auquel j'ai donné le nom de ''solénoïde électro-dynamique'', du mot grec σωληνοειδὴς, dont la signification exprime précisement ce qui a la forme d'un canal, c'est-à-dire la surface de cette forme sur laquelle se trouvent tous les circuits." (p. 267). English translation: "the assembly of all the circuits that surround it , assembly to which I gave the name ''electro-dynamic solenoid'', from the Greek word σωληνοειδὴς, whose meaning precisely expresses what has the shape of a channel, that is to say the surface of this shape on which all the circuits are located".</ref> The French term originally created by Ampère is ''solénoïde'', which is a French transliteration of the Greek word '']'' which means ''tubular''. | |||
| In ], the term refers to a coil whose length is substantially greater than its diameter, often wrapped around a ]lic core, which produces a uniform ] in a volume of space (where some experiment might be carried out) when an ] is passed through it. A solenoid is a type of ] when the purpose is to generate a controlled magnetic field. If the purpose of the solenoid is instead to impede changes in the electric current, a solenoid can be more specifically classified as an ] rather than an '''electromagnet'''. Not all electromagnets and inductors are solenoids; for example, the first electromagnet, invented in 1824, had a horseshoe rather than a cylindrical solenoid shape. | |||
| The helical coil of a solenoid does not necessarily need to revolve around a ] axis; for example, ]'s electromagnet of 1824 consisted of a solenoid bent into a horseshoe shape (similarly to an ]). | |||
| In ], the term may also refer to a variety of ] devices that convert ] into linear motion. The term is also often used to refer to a ], which is an integrated device containing an electromechanical solenoid which actuates either a ] or ] valve, or a solenoid switch, which is a specific type of ] that internally uses an electromechanical solenoid to operate an electrical switch; for example, an ], or a linear solenoid, which is an electromechanical solenoid. ]s, a type of electronic-mechanical locking mechanism, also exist. | |||
| Solenoids provide magnetic focusing of electrons in vacuums, notably in television camera tubes such as vidicons and image orthicons. Electrons take helical paths within the magnetic field. These solenoids, focus coils, surround nearly the whole length of the tube. | |||
| == Infinite continuous solenoid == | |||
| == Physics == | |||
| An infinite solenoid is a solenoid with infinite length but finite diameter. Continuous means that the solenoid is not formed by discrete finite-width coils but by infinitely many infinitely-thin coils with no space between them; in this abstraction, the solenoid is often viewed as a cylindrical sheet of conductive material. | |||
| === |
=== Infinite continuous solenoid === | ||
| ] |
] labelled ''a'', ''b'', and ''c''. Integrating over path ''c'' demonstrates that the magnetic field inside the solenoid must be radially uniform.]] | ||
| An infinite solenoid has infinite length but finite diameter. "Continuous" means that the solenoid is not formed by discrete finite-width coils but by many infinitely thin coils with no space between them; in this abstraction, the solenoid is often viewed as a cylindrical sheet of conductive material. | |||
| In short: the ] inside an infinitely long solenoid is homogeneous and its strength neither depends on the distance from the axis, nor on the solenoid's cross-sectional area. | |||
| The ] inside an infinitely long solenoid is homogeneous and its strength neither depends on the distance from the axis nor on the solenoid's cross-sectional area. | |||
| This is a derivation of the ] around a solenoid that is long enough so that fringe effects can be ignored. In Figure 1, we immediately know that the flux density vector points in the positive ''z'' direction inside the solenoid, and in the negative ''z'' direction outside the solenoid. We confirm this by applying the ] for the field around a wire. If we wrap our right hand around a wire with the thumb pointing in the direction of the current, the curl of the fingers shows how the field behaves. Since we are dealing with a long solenoid, all of the components of the magnetic field not pointing upwards cancel out by symmetry. Outside, a similar cancellation occurs, and the field is only pointing downwards. | |||
| This is a derivation of the ] around a solenoid that is long enough so that fringe effects can be ignored. In Figure 1, we immediately know that the flux density vector points in the positive ''z'' direction inside the solenoid, and in the negative ''z'' direction outside the solenoid. We confirm this by applying the ] for the field around a wire. If we wrap our right hand around a wire with the thumb pointing in the direction of the current, the curl of the fingers shows how the field behaves. Since we are dealing with a long solenoid, all of the components of the magnetic field not pointing upwards cancel out by symmetry. Outside, a similar cancellation occurs, and the field is only pointing downwards. | |||
| Now consider the imaginary loop ''c'' that is located inside the solenoid. By ], we know that the ] of '''B''' (the magnetic flux density vector) around this loop is zero, since it encloses no electrical currents (it can be also assumed that the circuital ] passing through the loop is constant under such conditions: a constant or constantly changing current through the solenoid). We have shown above that the field is pointing upwards inside the solenoid, so the horizontal portions of loop ''c'' do not contribute anything to the integral. Thus the integral of the up side 1 is equal to the integral of the down side 2. Since we can arbitrarily change the dimensions of the loop and get the same result, the only physical explanation is that the integrands are actually equal, that is, the magnetic field inside the solenoid is radially uniform. Note, though, that nothing prohibits it from varying longitudinally, which in fact it does. | |||
| Now consider the imaginary loop ''c'' that is located inside the solenoid. By ], we know that the ] of '''B''' (the magnetic flux density vector) around this loop is zero, since it encloses no electrical currents (it can be also assumed that the circuital ] passing through the loop is constant under such conditions: a constant or constantly changing current through the solenoid). We have shown above that the field is pointing upwards inside the solenoid, so the horizontal portions of loop ''c'' do not contribute anything to the integral. Thus the integral of the up side 1 is equal to the integral of the down side 2. Since we can arbitrarily change the dimensions of the loop and get the same result, the only physical explanation is that the integrands are actually equal, that is, the magnetic field inside the solenoid is radially uniform. Note, though, that nothing prohibits it from varying longitudinally, which in fact, it does. | |||
| === Outside === | |||
| A similar argument can be applied to the loop ''a'' to conclude that the field outside the solenoid is radially uniform or constant. This last result, which holds strictly true only near the centre of the solenoid where the field lines are parallel to its length, is important as it shows that the flux density outside is practically zero since the radii of the field outside the solenoid will tend to infinity. | |||
| An intuitive argument can also be used to show that the flux density outside the solenoid is actually zero. Magnetic field lines only exist as loops, they cannot diverge from or converge to a point like electric field lines can (see ]). The magnetic field lines follow the longitudinal path of the solenoid inside, so they must go in the opposite direction outside of the solenoid so that the lines can form |
A similar argument can be applied to the loop ''a'' to conclude that the field outside the solenoid is radially uniform or constant. This last result, which holds strictly true only near the center of the solenoid where the field lines are parallel to its length, is important as it shows that the flux density outside is practically zero since the radii of the field outside the solenoid will tend to infinity. An intuitive argument can also be used to show that the flux density outside the solenoid is actually zero. Magnetic field lines only exist as loops, they cannot diverge from or converge to a point like electric field lines can (see ]). The magnetic field lines follow the longitudinal path of the solenoid inside, so they must go in the opposite direction outside of the solenoid so that the lines can form loops. However, the volume outside the solenoid is much greater than the volume inside, so the density of magnetic field lines outside is greatly reduced. Now recall that the field outside is constant. In order for the total number of field lines to be conserved, the field outside must go to zero as the solenoid gets longer. Of course, if the solenoid is constructed as a wire spiral (as often done in practice), then it emanates an outside field the same way as a single wire, due to the current flowing overall down the length of the solenoid. | ||
| ] can be applied to the solenoid]] | |||
| Of course, if the solenoid is constructed as a wire spiral (as often done in practice), then it emanates an outside field the same way as a single wire, due to the current flowing overall down the length of the solenoid. | |||
| Applying ] to the solenoid (see figure on the right) gives us | |||
| === Quantitative description === | |||
| Now we can consider the imaginary loop ''b''. Take the line integral of '''B''' (the magnetic flux density vector) around the loop of length ''l''. The horizontal components vanish, and the field outside is practically zero, so ] gives us | |||
| :<math>B l= \mu_0 N I,</math> | :<math>B l= \mu_0 N I,</math> | ||
| where <math>\mu_0</math> is the ], <math>N</math> the number of turns, and <math>I</math> the current. | where <math>B</math> is the ], <math>l</math> is the length of the solenoid, <math>\mu_0</math> is the ], <math>N</math> the number of turns, and <math>I</math> the current. From this we get | ||
| From this we get | |||
| :<math>B = \mu_0 \frac{N I}{l}.</math> | :<math>B = \mu_0 \frac{N I}{l}.</math> | ||
| This equation is valid for a solenoid in free space, which means the permeability of the magnetic path is the same as permeability of free space, |
This equation is valid for a solenoid in free space, which means the ] of the magnetic path is the same as permeability of free space, μ<sub>0</sub>. | ||
| If the solenoid is immersed in a material with relative permeability |
If the solenoid is immersed in a material with relative permeability μ<sub>r</sub>, then the field is increased by that amount: | ||
| :<math>B = \mu_0 \mu_{\mathrm{r}} \frac{N I}{l}.</math> | :<math>B = \mu_0 \mu_{\mathrm{r}} \frac{N I}{l}.</math> | ||
| In most solenoids, the solenoid is not immersed in a higher permeability material, but rather some portion of the space around the solenoid has the higher permeability material and some is just air (which behaves much like free space). |
In most solenoids, the solenoid is not immersed in a higher permeability material, but rather some portion of the space around the solenoid has the higher permeability material and some is just air (which behaves much like free space). In that scenario, the full effect of the high permeability material is not seen, but there will be an effective (or apparent) permeability ''μ''<sub>eff</sub> such that 1 ≤ ''μ''<sub>eff</sub> ≤ ''μ''<sub>r</sub>. | ||
| The inclusion of a ] core, such as ], increases the magnitude of the magnetic flux density in the solenoid and raises the effective permeability of the magnetic path. This is expressed by the formula | The inclusion of a ] core, such as ], increases the magnitude of the magnetic flux density in the solenoid and raises the effective permeability of the magnetic path. This is expressed by the formula | ||
| :<math>B = \mu_0 \mu_{\mathrm{eff}} \frac{N I}{l} = \mu \frac{N I}{l},</math> | :<math>B = \mu_0 \mu_{\mathrm{eff}} \frac{N I}{l} = \mu \frac{N I}{l},</math> | ||
| where ''μ''<sub>eff</sub> is the effective or apparent permeability of the core. |
where ''μ''<sub>eff</sub> is the effective or apparent permeability of the core. The effective permeability is a function of the geometric properties of the core and its relative permeability. The terms relative permeability (a property of just the material) and effective permeability (a property of the whole structure) are often confused; they can differ by many orders of magnitude. | ||
| For an open magnetic structure, the relationship between the effective permeability and relative permeability is given as follows: | For an open magnetic structure, the relationship between the effective permeability and relative permeability is given as follows: | ||
| :<math>\mu_\mathrm{eff} = \frac{\mu_r}{1+k(\mu_r -1)},</math> |
:<math>\mu_\mathrm{eff} = \frac{\mu_r}{1+k(\mu_r -1)},</math> | ||
| where ''k'' is the |
where ''k'' is the demagnetization factor of the core.<ref>Jiles, David. Introduction to magnetism and magnetic materials. CRC press, p. 48, 2015.</ref> | ||
| == Finite continuous solenoid == | |||
| ] line and density created by a solenoid with surface ]]] | |||
| === Finite continuous solenoid === | |||
| A finite solenoid is a solenoid with finite length. Continuous means that the solenoid is not formed by discrete coils but by a sheet of conductive material. We assume the current is uniformly distributed on the surface of the solenoid, with a surface ] ''K''; in ]s: | A finite solenoid is a solenoid with finite length. Continuous means that the solenoid is not formed by discrete coils but by a sheet of conductive material. We assume the current is uniformly distributed on the surface of the solenoid, with a surface ] ''K''; in ]s: | ||
| <math display="block">\vec{K} = \frac{I}{l} \hat{\phi} .</math> | |||
| The magnetic field can be found using the ], which for a finite solenoid with radius '' |
The magnetic field can be found using the ], which for a finite solenoid with radius ''R'' and length ''l'' in cylindrical coordinates <math>(\rho, \phi, z)</math> is<ref>{{cite web |url=http://nukephysik101.files.wordpress.com/2011/07/finite-length-solenoid-potential-and-field.pdf |title=Archived copy |access-date=28 March 2013 |url-status=live |archive-url=https://web.archive.org/web/20140410113804/http://nukephysik101.files.wordpress.com/2011/07/finite-length-solenoid-potential-and-field.pdf |archive-date=10 April 2014 }}</ref><ref>{{cite web |url=http://nukephysik101.files.wordpress.com/2021/07/finite-length-solenoid-potential-and-field-1.pdf |title=Archived copy |access-date=10 July 2021 |url-status=live |archive-url=https://web.archive.org/web/20210719191335/https://nukephysik101.files.wordpress.com/2021/07/finite-length-solenoid-potential-and-field-1.pdf |archive-date=19 July 2021 }}</ref> | ||
| <math display="block">A_\phi = \frac{\mu_0 I}{\pi } \frac{R}{l} \left_{\zeta_-}^{\zeta_+},</math> | |||
| ] lines and density created by a solenoid with surface ]]] | |||
| :<math>A_\phi = \frac{\mu_0 I}{4\pi } \frac{1}{L} \sqrt{\frac{a}{\rho}} \left_{\zeta_-}^{\zeta_+},</math> | |||
| Where: | |||
| where | |||
| * <math>\zeta_{\pm}=z\pm \frac{l}{2}</math>, | |||
| * <math>n = \frac{4R\rho}{(R+\rho)^2}</math>, | |||
| * <math>m = \frac{4R\rho}{(R+\rho)^2+\zeta^2}</math>, | |||
| * <math>K(m)=\int_0^{\frac\pi 2}\frac{d\theta}{\sqrt{1-m \sin^2 \theta }}</math>, | |||
| * <math>E(m)=\int_0^{\frac\pi 2}{\sqrt{1-m \sin^2 \theta} } \,d\theta</math> , | |||
| * <math>\Pi(n,m)=\int_0^{\frac\pi 2}\frac{d\theta}{(1-n \sin^2 \theta)\sqrt{1-m \sin^2 \theta }}</math> . | |||
| Here, <math>K(m)</math>, <math>E(m)</math>, and <math>\Pi(n,m)</math> are complete ]s of the first, second, and third kind. | Here, <math>K(m)</math>, <math>E(m)</math>, and <math>\Pi(n,m)</math> are complete ]s of the first, second, and third kind. | ||
| Using | Using: | ||
| :<math>\vec{B} = \nabla \times \vec{A},</math> | |||
| the magnetic flux density is obtained as | |||
| :<math>B_\rho = \frac{\mu_0 I}{4\pi} \frac{1}{L} \sqrt{\frac{a}{\rho}} \left_{\zeta_-}^{\zeta_+},</math> | |||
| :<math>B_z =-\frac{\mu_0 I}{4\pi} \frac{1}{2L} \frac{1}{ \sqrt{a \rho}} \left_{\zeta_-}^{\zeta_+}.</math> | |||
| <math display="block">\vec{B} = \nabla \times \vec{A},</math> | |||
| == Inductance == | |||
| The magnetic flux density is obtained as<ref>{{cite journal |first1=Karl Friedrich |last1=Müller |title=Berechnung der Induktivität von Spulen |language=de |trans-title=Calculating the Inductance of Coils |journal=Archiv für Elektrotechnik |volume=17 |issue=3 |date=1 May 1926 |pages=336–353 |issn=1432-0487 |doi=10.1007/BF01655986 |s2cid=123686159 }}</ref><ref>{{cite journal |first1=Edmund E. |last1=Callaghan |first2=Stephen H. |last2=Maslen |title=The magnetic field of a finite solenoid |language=en |journal=NASA Technical Reports |volume=NASA-TN-D-465 |issue=E-900 |date=1 October 1960 |url=https://ntrs.nasa.gov/search.jsp?R=19980227402}}</ref><ref name="CaciagliBaars2018">{{cite journal |last1=Caciagli|first1=Alessio |last2=Baars|first2=Roel J. |last3=Philipse|first3=Albert P. |last4=Kuipers|first4=Bonny W.M. |title=Exact expression for the magnetic field of a finite cylinder with arbitrary uniform magnetization |journal=Journal of Magnetism and Magnetic Materials | volume=456 | year=2018|pages=423–432 | issn=0304-8853 | doi=10.1016/j.jmmm.2018.02.003 | bibcode=2018JMMM..456..423C |hdl=1874/363313 | s2cid=126037802|hdl-access=free }}</ref> | |||
| <math display="block">B_\rho = \frac{\mu_0 I}{4\pi} \frac{1}{l\,\rho} \left_{\zeta_-}^{\zeta_+},</math> | |||
| <math display="block">B_z = \frac{\mu_0 I}{2\pi} \frac{1}{l} \left_{\zeta_-}^{\zeta_+}.</math> | |||
| On the symmetry axis, the radial component vanishes, and the axial field component is | |||
| <math display="block">B_z = \frac{\mu_0 NI}{2}\left( \frac{z+l/2}{l \sqrt{R^2+(z+l/2)^2}} - \frac{z-l/2}{l \sqrt{R^2+(z-l/2)^2}}\right).</math> | |||
| Inside the solenoid, far away from the ends (<math>l/2 - |z| \gg R</math>), this tends towards the constant value <math>B = \mu_0 N I/l</math>. | |||
| === Short solenoid estimate === | |||
| For the case in which the radius is much larger than the length of the solenoid (<math>R \gg l</math>), the magnetic flux density through the centre of the solenoid (in the ''z'' direction, parallel to the solenoid's length, where the coil is centered at ''z''=0) can be estimated as the flux density of a single circular conductor loop: | |||
| :<math>B_z \approx \frac{\mu_0 INR^2}{2\sqrt{R^2+z^2}^3} </math> | |||
| === Irregular solenoids === | |||
| ] | |||
| Within the category of finite solenoids, there are those that are sparsely wound with a single pitch, those that are sparsely wound with varying pitches (varied-pitch solenoid), and those with varying radii for different loops (non-cylindrical solenoids). They are called ''irregular solenoids''. They have found applications in different areas, such as sparsely wound solenoids for ],<ref>{{cite journal |first1=André |last1=Kurs |first2=Aristeidis |last2=Karalis |first3=Robert |last3=Moffatt |first4=J. D. |last4=Joannopoulos |first5=Peter |last5=Fisher |first6=Marin |last6=Soljačić |title=Wireless Power Transfer via Strongly Coupled Magnetic Resonances |journal=Science |volume=317 |issue=5834 |date=6 July 2007 |pages=83–86 |doi=10.1126/science.1143254|pmid=17556549 |bibcode=2007Sci...317...83K |s2cid=17105396 |doi-access=free }}</ref><ref>{{cite journal |first1=Wenshen |last1=Zhou |first2=Shao Ying |last2=Huang |title=Novel coil design for wideband wireless power transfer |journal=2017 International Applied Computational Electromagnetics Society Symposium (ACES) |date= 28 September 2017 |pages=1–2 |url=https://ieeexplore.ieee.org/document/8051697}}</ref> varied-pitch solenoids for magnetic resonance imaging (MRI),<ref>{{cite journal |first1=Zhi Hua |last1=Ren |first2=Shao Ying |last2=Huang |title=The design of a short solenoid with homogeneous B1 for a low-field portable MRI scanner using genetic algorithm |journal=Proc. 26th ISMRM |date=August 2018 |pages=1720 |url=https://cds.ismrm.org/protected/18MPresentations/abstracts/1720.html }}{{Dead link|date=September 2023 |bot=InternetArchiveBot |fix-attempted=yes }}</ref> and non-cylindrical solenoids for other medical devices.<ref>{{cite journal |first1=L. |last1=Jian |first2=Y. |last2=Shi |first3=J. |last3=Liang |first4=C. |last4=Liu|first5=G. |last5=Xu|title=A Novel Targeted Magnetic Fluid Hyperthermia System Using HTS Coil Array for Tumor Treatment |journal=IEEE Transactions on Applied Superconductivity |volume=23 |issue=3 |date=June 2013 |pages=4400104 |doi=10.1109/TASC.2012.2230051|bibcode=2013ITAS...23Q0104J |s2cid=44197357 }}</ref> | |||
| The calculation of the intrinsic inductance and capacitance cannot be done using those for the conventional solenoids, i.e. the tightly wound ones. New calculation methods were proposed for the calculation of intrinsic inductance<ref>{{cite journal |first1=Wenshen |last1=Zhou |first2=Shao Ying |last2=Huang|title=An Accurate Model for Fast Calculating the Resonant Frequency of an Irregular Solenoid |journal=IEEE Transactions on Microwave Theory and Techniques |volume=67 |issue=7 |date= July 2019|pages=2663–2673|doi=10.1109/TMTT.2019.2915514|bibcode=2019ITMTT..67.2663Z |s2cid=182038533 }}</ref>(codes available at <ref>{{cite journal |first1=Wenshen |last1=Zhou |first2=Shao Ying |last2=Huang |title=the code for accurate model for fast calculating the resonant frequency of an irregular solenoid |date=12 April 2021 |url=https://github.com/wszhou/SRF_calculation}}</ref>) and capacitance.<ref>{{cite journal |first1=Wenshen |last1=Zhou |first2=Shao Ying |last2=Huang |title=Modeling the Self-Capacitance of an Irregular Solenoid |journal=IEEE Transactions on Electromagnetic Compatibility |date= October 2020 |volume=63 |issue=3 |pages=783–791 |doi=10.1109/TEMC.2020.3031075|issn=0018-9375|s2cid=229274298 }}</ref> (codes available at <ref>{{cite journal |first1=Wenshen |last1=Zhou |first2=Shao Ying |last2=Huang |title=the code for accurate model for self-capacitance of irregular solenoids |date=12 April 2021 |url=https://github.com/wszhou/capacitance_calc}}</ref>) | |||
| === Inductance === | |||
| {{See also|Inductance with physical symmetry}} | {{See also|Inductance with physical symmetry}} | ||
| As shown above, the magnetic flux density <math>B</math> within the coil is practically constant and given by | As shown above, the magnetic flux density <math>B</math> within the coil is practically constant and given by | ||
| :<math>B = \mu_0 \frac{ |
:<math>B = \mu_0 \frac{NI}{l},</math> | ||
| where ''μ''<sub>0</sub> is the ], <math>N</math> the number of turns, <math> |
where ''μ''<sub>0</sub> is the ], <math>N</math> the number of turns, <math>I</math> the current and <math>l</math> the length of the coil. Ignoring end effects, the total ] through the coil is obtained by multiplying the flux density <math>B</math> by the cross-section area <math>A</math>: | ||
| :<math>\Phi = \mu_0 \frac{ |
:<math>\Phi = \mu_0 \frac{NIA}{l}.</math> | ||
| Combining this with the definition of ] | Combining this with the definition of ] | ||
| :<math>L = \frac{N \Phi}{ |
:<math>L = \frac{N \Phi}{I},</math> | ||
| the inductance of a solenoid follows as | the inductance of a solenoid follows as | ||
| :<math>L = \mu_0 \frac{N^2A}{l}.</math> | :<math>L = \mu_0 \frac{N^2A}{l}.</math> | ||
| A table of inductance for short solenoids of various diameter to length ratios has been calculated by Dellinger, Whittmore, and Ould.<ref>{{cite |
A table of inductance for short solenoids of various diameter to length ratios has been calculated by Dellinger, Whittmore, and Ould.<ref>{{cite book |url= https://books.google.com/books?id=Xn8KbsgeFrwC&pg=PA248 |title=Radio Instruments and Measurements |author1=D. Howard Dellinger |author2=L. E. Whittmore |author3=R. S. Ould |name-list-style=amp |year= 1924 |journal=NBS Circular |volume= C74 |access-date=7 September 2009 |isbn=9780849302527 }}</ref> | ||
| This, and the inductance of more complicated shapes, can be derived from ]. For rigid air-core coils, inductance is a function of coil geometry and number of turns, and is independent of current. | This, and the inductance of more complicated shapes, can be derived from ]. For rigid air-core coils, inductance is a function of coil geometry and number of turns, and is independent of current. | ||
| Line 98: | Line 113: | ||
| Similar analysis applies to a solenoid with a magnetic core, but only if the length of the coil is much greater than the product of the relative ] of the magnetic core and the diameter. That limits the simple analysis to low-permeability cores, or extremely long thin solenoids. The presence of a core can be taken into account in the above equations by replacing the magnetic constant ''μ<sub>0</sub>'' with ''μ'' or ''μ<sub>0</sub>μ<sub>r</sub>'', where ''μ'' represents permeability and ''μ<sub>r</sub>'' ]. Note that since the permeability of ] materials changes with applied magnetic flux, the inductance of a coil with a ferromagnetic core will generally vary with current. | Similar analysis applies to a solenoid with a magnetic core, but only if the length of the coil is much greater than the product of the relative ] of the magnetic core and the diameter. That limits the simple analysis to low-permeability cores, or extremely long thin solenoids. The presence of a core can be taken into account in the above equations by replacing the magnetic constant ''μ<sub>0</sub>'' with ''μ'' or ''μ<sub>0</sub>μ<sub>r</sub>'', where ''μ'' represents permeability and ''μ<sub>r</sub>'' ]. Note that since the permeability of ] materials changes with applied magnetic flux, the inductance of a coil with a ferromagnetic core will generally vary with current. | ||
| == |
== See also == | ||
| === Electromechanical solenoid === | |||
| ] | |||
| Electromechanical solenoids consist of an electromagnetically inductive coil, wound around a movable ] or ] slug (termed the armature). The coil is shaped such that the ] can be moved in and out of the center, altering the coil's inductance and thereby becoming an ]. The armature is used to provide a mechanical force to some mechanism (such as controlling a ]). Although typically weak over anything but very short distances, solenoids may be controlled directly by a controller circuit, and thus have very quick reaction times. | |||
| The force applied to the armature is proportional to the change in inductance of the coil with respect to the change in position of the armature, and the current flowing through the coil (see ]). The force applied to the armature will always move the armature in a direction that increases the coil's inductance. | |||
| Electromechanical solenoids are commonly seen in electronic ]s, ]s, ]s and ]. | |||
| Proportional Solenoid - | |||
| Included in this category of solenoids are the uniquely designed magnetic circuits that effect analog positioning of the solenoid plunger or armature as a function of coil current. These solenoids, whether axial or rotary, employ a flux carrying geometry that both produces a high starting force (torque), and has a section that quickly begins to saturate magnetically. The resulting force (torque) profile as the solenoid progresses through its operational stroke is nearly flat or descends from a high to a lower value. The solenoid can be useful for positioning, stopping mid-stroke, or for low velocity actuation; especially in a closed loop control system. A uni-directional solenoid would actuate against an opposing force or a dual solenoid system would be self cycling. The proportional concept is more fully described in SAE publication 860759 (1986). | |||
| === Rotary solenoid === | |||
| The rotary solenoid is an electromechanical device used to rotate a ratcheting mechanism when power is applied. These were used in the 1950s for rotary snap-switch automation in electromechanical controls. Repeated actuation of the rotary solenoid advances the snap-switch forward one position. Two rotary actuators on opposite ends of the rotary snap-switch shaft, can advance or reverse the switch position. | |||
| The rotary solenoid has a similar appearance to a linear solenoid, except that the core is mounted in the center of a large flat disk, with two or three inclined grooves cut into the underside of the disk. These grooves align with slots on the solenoid body, with ball bearings in the grooves. | |||
| When the solenoid is activated, the core is drawn into the coil, and the disk rotates on the ball bearings in the grooves as it moves towards the coil body. When power is removed, a spring on the disk rotates it back to its starting position, also pulling the core out of the coil. | |||
| The rotary solenoid was invented in 1944 by George H. Leland, of Dayton, Ohio, to provide a more reliable and shock/vibration tolerant release mechanism for air-dropped bombs. Previously used linear (axial) solenoids were prone to inadvertent releases. U.S. Patent number 2,496,880 describes the electromagnet and inclined raceways that are the basis of the invention. Leland's engineer, Earl W. Kerman, was instrumental in developing a compatible bomb release shackle that incorporated the rotary solenoid. Bomb shackles of this type are found in a B-29 aircraft fuselage on display at the National Museum of the USAF in Dayton, Ohio. Solenoids of this variety continue to be used in countless modern applications, and are still manufactured under Leland's original brand "Ledex", now owned by ]. | |||
| === Rotary voice coil === | |||
| A rotary ] is a rotational version of a solenoid. Typically the fixed magnet is on the outside, and the coil part moves in an arc controlled by the current flow through the coils. Rotary voice coils are widely employed in devices such as ]s.{{citation needed|date=October 2013}} The working part of a ] is also a type of rotary voice coil that pivots around the pointer axis, a hairspring is usually used to provide a weak nearly linear restoring force. | |||
| === Pneumatic solenoid valve === | |||
| A ] ] is a switch for routing air to any pneumatic device, usually an ], allowing a relatively small signal to control a large device. It is also the interface between electronic controllers and pneumatic systems.{{citation needed|date=October 2013}} | |||
| === Hydraulic solenoid valve === | |||
| ] are in general similar to pneumatic solenoid valves except that they control the flow of ] (oil), often at around 3000 psi (210 bar, 21 MPa, 21 MN/m²). ] uses solenoids to control the flow of oil to rams or actuators. Solenoid-controlled valves are often used in irrigation systems, where a relatively weak solenoid opens and closes a small pilot valve, which in turn activates the main valve by applying fluid pressure to a piston or diaphragm that is mechanically coupled to the main valve. | |||
| Solenoids are also in everyday household items such as washing machines to control the flow and amount of water into the drum. | |||
| ] control fluid flow through an automatic transmission and are typically installed in the transmission valve body. | |||
| === Automobile starter solenoid === | |||
| {{Main|Starter solenoid}} | |||
| In a car or truck, the starter solenoid is part of an ] starting system. The starter solenoid receives a large ] from the ] and a small electric current from the ]. When the ignition switch is turned on (i.e. when the key is turned to start the car), the small electric current forces the starter solenoid to close a pair of heavy contacts, thus relaying the large electric current to the ]. | |||
| Starter solenoids can also be built into the starter itself, often visible on the outside of the starter. If a starter solenoid receives insufficient power from the battery, it will fail to start the ], and may produce a rapid 'clicking' or 'clacking' sound. This can be caused by a low or dead battery, by ] or loose connections in the cable, or by a broken or damaged positive (red) cable from the battery. Any of these will result in some power to the solenoid, but not enough to hold the heavy contacts closed, so the starter motor itself never spins, and the engine doesn't start. | |||
| == See also == | |||
| * ] | |||
| * ] | |||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | |||
| == References == | == References == | ||
| {{ |
{{refs}} | ||
| == External links == | == External links == | ||
| {{ |
{{commonscat|Solenoids}} | ||
| * , National High Magnetic Field Laboratory | |||
| * , National High Magnetic Field Laboratory | |||
| * | * | ||
| * | |||
| * | |||
| * | |||
| * | |||
| {{Use dmy dates|date=September |
{{Use dmy dates|date=September 2019}} | ||
| {{Authority control}} | {{Authority control}} | ||
Latest revision as of 13:03, 18 December 2024
Type of electromagnet formed by a coil of wire This article is about the electromagnet. For the device that converts electricity to mechanical energy, see solenoid (engineering). For other uses, see Solenoid (disambiguation).

A solenoid (/ˈsoʊlənɔɪd/) is a type of electromagnet formed by a helical coil of wire whose length is substantially greater than its diameter, which generates a controlled magnetic field. The coil can produce a uniform magnetic field in a volume of space when an electric current is passed through it.
André-Marie Ampère coined the term solenoid in 1823, having conceived of the device in 1820. The French term originally created by Ampère is solénoïde, which is a French transliteration of the Greek word σωληνοειδὴς which means tubular.
The helical coil of a solenoid does not necessarily need to revolve around a straight-line axis; for example, William Sturgeon's electromagnet of 1824 consisted of a solenoid bent into a horseshoe shape (similarly to an arc spring).
Solenoids provide magnetic focusing of electrons in vacuums, notably in television camera tubes such as vidicons and image orthicons. Electrons take helical paths within the magnetic field. These solenoids, focus coils, surround nearly the whole length of the tube.
Physics
Infinite continuous solenoid

An infinite solenoid has infinite length but finite diameter. "Continuous" means that the solenoid is not formed by discrete finite-width coils but by many infinitely thin coils with no space between them; in this abstraction, the solenoid is often viewed as a cylindrical sheet of conductive material.
The magnetic field inside an infinitely long solenoid is homogeneous and its strength neither depends on the distance from the axis nor on the solenoid's cross-sectional area.
This is a derivation of the magnetic flux density around a solenoid that is long enough so that fringe effects can be ignored. In Figure 1, we immediately know that the flux density vector points in the positive z direction inside the solenoid, and in the negative z direction outside the solenoid. We confirm this by applying the right hand grip rule for the field around a wire. If we wrap our right hand around a wire with the thumb pointing in the direction of the current, the curl of the fingers shows how the field behaves. Since we are dealing with a long solenoid, all of the components of the magnetic field not pointing upwards cancel out by symmetry. Outside, a similar cancellation occurs, and the field is only pointing downwards.
Now consider the imaginary loop c that is located inside the solenoid. By Ampère's law, we know that the line integral of B (the magnetic flux density vector) around this loop is zero, since it encloses no electrical currents (it can be also assumed that the circuital electric field passing through the loop is constant under such conditions: a constant or constantly changing current through the solenoid). We have shown above that the field is pointing upwards inside the solenoid, so the horizontal portions of loop c do not contribute anything to the integral. Thus the integral of the up side 1 is equal to the integral of the down side 2. Since we can arbitrarily change the dimensions of the loop and get the same result, the only physical explanation is that the integrands are actually equal, that is, the magnetic field inside the solenoid is radially uniform. Note, though, that nothing prohibits it from varying longitudinally, which in fact, it does.
A similar argument can be applied to the loop a to conclude that the field outside the solenoid is radially uniform or constant. This last result, which holds strictly true only near the center of the solenoid where the field lines are parallel to its length, is important as it shows that the flux density outside is practically zero since the radii of the field outside the solenoid will tend to infinity. An intuitive argument can also be used to show that the flux density outside the solenoid is actually zero. Magnetic field lines only exist as loops, they cannot diverge from or converge to a point like electric field lines can (see Gauss's law for magnetism). The magnetic field lines follow the longitudinal path of the solenoid inside, so they must go in the opposite direction outside of the solenoid so that the lines can form loops. However, the volume outside the solenoid is much greater than the volume inside, so the density of magnetic field lines outside is greatly reduced. Now recall that the field outside is constant. In order for the total number of field lines to be conserved, the field outside must go to zero as the solenoid gets longer. Of course, if the solenoid is constructed as a wire spiral (as often done in practice), then it emanates an outside field the same way as a single wire, due to the current flowing overall down the length of the solenoid.
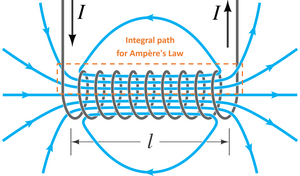
Applying Ampère's circuital law to the solenoid (see figure on the right) gives us
where is the magnetic flux density, is the length of the solenoid, is the magnetic constant, the number of turns, and the current. From this we get
This equation is valid for a solenoid in free space, which means the permeability of the magnetic path is the same as permeability of free space, μ0.
If the solenoid is immersed in a material with relative permeability μr, then the field is increased by that amount:
In most solenoids, the solenoid is not immersed in a higher permeability material, but rather some portion of the space around the solenoid has the higher permeability material and some is just air (which behaves much like free space). In that scenario, the full effect of the high permeability material is not seen, but there will be an effective (or apparent) permeability μeff such that 1 ≤ μeff ≤ μr.
The inclusion of a ferromagnetic core, such as iron, increases the magnitude of the magnetic flux density in the solenoid and raises the effective permeability of the magnetic path. This is expressed by the formula
where μeff is the effective or apparent permeability of the core. The effective permeability is a function of the geometric properties of the core and its relative permeability. The terms relative permeability (a property of just the material) and effective permeability (a property of the whole structure) are often confused; they can differ by many orders of magnitude.
For an open magnetic structure, the relationship between the effective permeability and relative permeability is given as follows:
where k is the demagnetization factor of the core.
Finite continuous solenoid
A finite solenoid is a solenoid with finite length. Continuous means that the solenoid is not formed by discrete coils but by a sheet of conductive material. We assume the current is uniformly distributed on the surface of the solenoid, with a surface current density K; in cylindrical coordinates:
The magnetic field can be found using the vector potential, which for a finite solenoid with radius R and length l in cylindrical coordinates is

Where:
- ,
- ,
- ,
- ,
- ,
- .
Here, , , and are complete elliptic integrals of the first, second, and third kind.
Using:
The magnetic flux density is obtained as
On the symmetry axis, the radial component vanishes, and the axial field component is Inside the solenoid, far away from the ends (), this tends towards the constant value .
Short solenoid estimate
For the case in which the radius is much larger than the length of the solenoid (), the magnetic flux density through the centre of the solenoid (in the z direction, parallel to the solenoid's length, where the coil is centered at z=0) can be estimated as the flux density of a single circular conductor loop:
Irregular solenoids

Within the category of finite solenoids, there are those that are sparsely wound with a single pitch, those that are sparsely wound with varying pitches (varied-pitch solenoid), and those with varying radii for different loops (non-cylindrical solenoids). They are called irregular solenoids. They have found applications in different areas, such as sparsely wound solenoids for wireless power transfer, varied-pitch solenoids for magnetic resonance imaging (MRI), and non-cylindrical solenoids for other medical devices.
The calculation of the intrinsic inductance and capacitance cannot be done using those for the conventional solenoids, i.e. the tightly wound ones. New calculation methods were proposed for the calculation of intrinsic inductance(codes available at ) and capacitance. (codes available at )
Inductance
See also: Inductance with physical symmetryAs shown above, the magnetic flux density within the coil is practically constant and given by
where μ0 is the magnetic constant, the number of turns, the current and the length of the coil. Ignoring end effects, the total magnetic flux through the coil is obtained by multiplying the flux density by the cross-section area :
Combining this with the definition of inductance
the inductance of a solenoid follows as
A table of inductance for short solenoids of various diameter to length ratios has been calculated by Dellinger, Whittmore, and Ould.
This, and the inductance of more complicated shapes, can be derived from Maxwell's equations. For rigid air-core coils, inductance is a function of coil geometry and number of turns, and is independent of current.
Similar analysis applies to a solenoid with a magnetic core, but only if the length of the coil is much greater than the product of the relative permeability of the magnetic core and the diameter. That limits the simple analysis to low-permeability cores, or extremely long thin solenoids. The presence of a core can be taken into account in the above equations by replacing the magnetic constant μ0 with μ or μ0μr, where μ represents permeability and μr relative permeability. Note that since the permeability of ferromagnetic materials changes with applied magnetic flux, the inductance of a coil with a ferromagnetic core will generally vary with current.
See also
References
- "solenoid: Meaning in the Cambridge English Dictionary". dictionary.cambridge.org. Archived from the original on 16 January 2017. Retrieved 16 January 2017.
- or equivalently, the diameter of the coil is assumed to be infinitesimally small (Ampère 1823, p. 267: "des courants électriques formants de très-petits circuits autour de cette ligne, dans des plans infiniment rapprochés qui lui soient perpendiculaires").
- Session of the Académie des sciences of 22 December 1823, published in print in: Ampère, "Mémoire sur la théorie mathématique des phénomènes électro-dynamiques", Mémoires de l'Académie royale des sciences de l'Institut de France 6 (1827), Paris, F. Didot, pp. 267ff. (and figs. 29–33). "l'assemblage de tous les circuits qui l'entourent , assemblage auquel j'ai donné le nom de solénoïde électro-dynamique, du mot grec σωληνοειδὴς, dont la signification exprime précisement ce qui a la forme d'un canal, c'est-à-dire la surface de cette forme sur laquelle se trouvent tous les circuits." (p. 267). English translation: "the assembly of all the circuits that surround it , assembly to which I gave the name electro-dynamic solenoid, from the Greek word σωληνοειδὴς, whose meaning precisely expresses what has the shape of a channel, that is to say the surface of this shape on which all the circuits are located".
- Jiles, David. Introduction to magnetism and magnetic materials. CRC press, p. 48, 2015.
- "Archived copy" (PDF). Archived (PDF) from the original on 10 April 2014. Retrieved 28 March 2013.
{{cite web}}: CS1 maint: archived copy as title (link) - "Archived copy" (PDF). Archived (PDF) from the original on 19 July 2021. Retrieved 10 July 2021.
{{cite web}}: CS1 maint: archived copy as title (link) - Müller, Karl Friedrich (1 May 1926). "Berechnung der Induktivität von Spulen" [Calculating the Inductance of Coils]. Archiv für Elektrotechnik (in German). 17 (3): 336–353. doi:10.1007/BF01655986. ISSN 1432-0487. S2CID 123686159.
- Callaghan, Edmund E.; Maslen, Stephen H. (1 October 1960). "The magnetic field of a finite solenoid". NASA Technical Reports. NASA-TN-D-465 (E-900).
- Caciagli, Alessio; Baars, Roel J.; Philipse, Albert P.; Kuipers, Bonny W.M. (2018). "Exact expression for the magnetic field of a finite cylinder with arbitrary uniform magnetization". Journal of Magnetism and Magnetic Materials. 456: 423–432. Bibcode:2018JMMM..456..423C. doi:10.1016/j.jmmm.2018.02.003. hdl:1874/363313. ISSN 0304-8853. S2CID 126037802.
- Kurs, André; Karalis, Aristeidis; Moffatt, Robert; Joannopoulos, J. D.; Fisher, Peter; Soljačić, Marin (6 July 2007). "Wireless Power Transfer via Strongly Coupled Magnetic Resonances". Science. 317 (5834): 83–86. Bibcode:2007Sci...317...83K. doi:10.1126/science.1143254. PMID 17556549. S2CID 17105396.
- Zhou, Wenshen; Huang, Shao Ying (28 September 2017). "Novel coil design for wideband wireless power transfer". 2017 International Applied Computational Electromagnetics Society Symposium (ACES): 1–2.
- Ren, Zhi Hua; Huang, Shao Ying (August 2018). "The design of a short solenoid with homogeneous B1 for a low-field portable MRI scanner using genetic algorithm". Proc. 26th ISMRM: 1720.
- Jian, L.; Shi, Y.; Liang, J.; Liu, C.; Xu, G. (June 2013). "A Novel Targeted Magnetic Fluid Hyperthermia System Using HTS Coil Array for Tumor Treatment". IEEE Transactions on Applied Superconductivity. 23 (3): 4400104. Bibcode:2013ITAS...23Q0104J. doi:10.1109/TASC.2012.2230051. S2CID 44197357.
- Zhou, Wenshen; Huang, Shao Ying (July 2019). "An Accurate Model for Fast Calculating the Resonant Frequency of an Irregular Solenoid". IEEE Transactions on Microwave Theory and Techniques. 67 (7): 2663–2673. Bibcode:2019ITMTT..67.2663Z. doi:10.1109/TMTT.2019.2915514. S2CID 182038533.
- Zhou, Wenshen; Huang, Shao Ying (12 April 2021). "the code for accurate model for fast calculating the resonant frequency of an irregular solenoid".
{{cite journal}}: Cite journal requires|journal=(help) - Zhou, Wenshen; Huang, Shao Ying (October 2020). "Modeling the Self-Capacitance of an Irregular Solenoid". IEEE Transactions on Electromagnetic Compatibility. 63 (3): 783–791. doi:10.1109/TEMC.2020.3031075. ISSN 0018-9375. S2CID 229274298.
- Zhou, Wenshen; Huang, Shao Ying (12 April 2021). "the code for accurate model for self-capacitance of irregular solenoids".
{{cite journal}}: Cite journal requires|journal=(help) - D. Howard Dellinger; L. E. Whittmore & R. S. Ould (1924). Radio Instruments and Measurements. Vol. C74. ISBN 9780849302527. Retrieved 7 September 2009.
{{cite book}}:|journal=ignored (help)
External links
- Interactive Java Tutorial: Magnetic Field of a Solenoid, National High Magnetic Field Laboratory
- Discussion of Solenoids at Hyperphysics
Categories:

 is the
is the  is the length of the solenoid,
is the length of the solenoid,  is the
is the  the number of turns, and
the number of turns, and  the current. From this we get
the current. From this we get





 is
is

 ,
, ,
, ,
, ,
, ,
, .
. ,
,  , and
, and  are complete
are complete 


 Inside the solenoid, far away from the ends (
Inside the solenoid, far away from the ends ( ), this tends towards the constant value
), this tends towards the constant value  .
.
 ), the magnetic flux density through the centre of the solenoid (in the z direction, parallel to the solenoid's length, where the coil is centered at z=0) can be estimated as the flux density of a single circular conductor loop:
), the magnetic flux density through the centre of the solenoid (in the z direction, parallel to the solenoid's length, where the coil is centered at z=0) can be estimated as the flux density of a single circular conductor loop:


 :
:


