| Revision as of 00:21, 31 October 2019 edit66.215.65.3 (talk)No edit summaryTag: Visual edit← Previous edit | Latest revision as of 16:53, 28 December 2024 edit undoConstant314 (talk | contribs)Extended confirmed users, Pending changes reviewers, Rollbackers13,399 edits Restored revision 1265751023 by 2A00:23C8:9883:A001:45B:C2FF:3319:3165 (talk): This article is about capacitance, not capacitors. The onus for a consensus is on the editor ading the material.Tags: Twinkle Undo | ||
| (172 intermediate revisions by 90 users not shown) | |||
| Line 1: | Line 1: | ||
| {{ |
{{Short description|Ability of a body to store an electrical charge}} | ||
| {{For|capacitance of blood vessels|Compliance (physiology)}} | |||
| {{Use dmy dates|date=June 2013}} | |||
| {{Use dmy dates|date=June 2020}} | |||
| {{Infobox physical quantity | {{Infobox physical quantity | ||
| | name = | | name = | ||
| Line 9: | Line 10: | ||
| | unit = ] | | unit = ] | ||
| | otherunits =μF, nF, pF | | otherunits =μF, nF, pF | ||
| | symbols = ''C'' | | symbols = {{math|''C''}} | ||
| | baseunits = F = A<sup>2</sup> s<sup>4</sup> kg<sup>−1</sup> m<sup>−2</sup> | | baseunits = F = A<sup>2</sup> s<sup>4</sup> kg<sup>−1</sup> m<sup>−2</sup> | ||
| | dimension = wikidata | |||
| | dimension = '''M'''<sup>−1</sup> '''L'''<sup>−2</sup> '''T'''<sup>4</sup> '''I'''<sup>2</sup> | |||
| | derivations = ''C'' = ''']''' / ''']''' | | derivations = ''C'' = ''']''' / ''']''' | ||
| }} | }} | ||
| {{Electromagnetism |Network}} | {{Electromagnetism |Network}} | ||
| '''Capacitance''' is the |
'''Capacitance''' is the ability of an object to store ]. It is measured by the charge in response to a difference in ], expressed as the ratio of those quantities. Commonly recognized are two closely related notions of capacitance: ''self capacitance'' and ''mutual capacitance''.<ref name=Harrington_2003>{{cite book |last=Harrington |first=Roger F. |author-link=Roger F. Harrington |title=Introduction to Electromagnetic Engineering |publisher=Dover Publications |year=2003 |edition=1st |page=43 |isbn=0-486-43241-6}}</ref>{{rp|237–238}} An object that can be electrically charged exhibits self capacitance, for which the electric potential is measured between the object and ground. Mutual capacitance is measured between two components, and is particularly important in the operation of the ], an elementary ] ] designed to add capacitance to an ]. | ||
| The capacitance |
The capacitance between two ] depends only on the geometry; the opposing surface area of the conductors and the distance between them; and the ] of any ] material between them. For many dielectric materials, the permittivity, and thus the capacitance, is independent of the potential difference between the conductors and the total charge on them. | ||
| The ] unit of capacitance is the ] (symbol: F), named after the English physicist ]. A 1 farad capacitor, when charged with 1 ] of electrical charge, has a potential difference of 1 ] between its plates.<ref>{{cite web |url=http://www.collinsdictionary.com/dictionary/english/farad |title=Definition of 'farad' |publisher=Collins}}</ref> The reciprocal of capacitance is called ]. | The ] unit of capacitance is the ] (symbol: F), named after the English physicist ].<ref name="NSW" /> A 1 farad capacitor, when charged with 1 ] of electrical charge, has a potential difference of 1 ] between its plates.<ref>{{cite web |url=http://www.collinsdictionary.com/dictionary/english/farad |title=Definition of 'farad' |publisher=Collins}}</ref> The reciprocal of capacitance is called ]. | ||
| ==Self capacitance== | ==Self capacitance== | ||
| In electrical circuits, the term ''capacitance'' is usually a shorthand for the |
In discussing electrical circuits, the term ''capacitance'' is usually a shorthand for the mutual capacitance between two adjacent conductors, such as the two plates of a capacitor. However, every isolated conductor also exhibits capacitance, here called ''self capacitance''. It is measured by the amount of electric charge that must be added to an isolated conductor to raise its ] by one unit of measurement, e.g., one ].<ref>{{cite book|author=William D. Greason| title=Electrostatic discharge in electronics|url=https://books.google.com/books?id=404fAQAAIAAJ|year=1992|publisher=Research Studies Press|isbn=978-0-86380-136-5 |page=48}}</ref> The reference point for this potential is a theoretical hollow conducting sphere, of infinite radius, with the conductor centered inside this sphere. | ||
| Self capacitance of a conductor is defined by the ratio of charge and electric potential: | |||
| <math display="block">C = \frac{q}{V},</math> | |||
| where | where | ||
| *<math display="inline">q</math> is the charge held, | |||
| *<big><math display="inline">V = \frac{1}{4\pi\varepsilon_0}\int \frac{\sigma}{r}\,dS</math></big> is the electric potential, | |||
| *<math display="inline">\sigma</math> is the surface charge density, | |||
| *<math display="inline">dS</math> is an infinitesimal element of area on the surface of the conductor, over which the surface charge density is integrated, | |||
| *<math display="inline">r</math> is the length from <math display="inline">dS</math> to a fixed point ''M'' on the conductor, | |||
| *<math>\varepsilon_0</math> is the ]. | |||
| Using this method, the self capacitance of a conducting sphere of radius |
Using this method, the self capacitance of a conducting sphere of radius <math display="inline">R</math> in free space (i.e. far away from any other charge distributions) is:<ref name=NSW>{{cite web|archive-url= https://web.archive.org/web/20090226225105/http://www.phys.unsw.edu.au/COURSES/FIRST_YEAR/pdf%20files/5Capacitanceanddielectr.pdf|archive-date=2009-02-26|url=http://www.phys.unsw.edu.au/COURSES/FIRST_YEAR/pdf%20files/5Capacitanceanddielectr.pdf|title=Lecture notes: Capacitance and Dieletrics|publisher=University of New South Wales}}</ref> | ||
| <math display="block">C = 4 \pi \varepsilon_0 R.</math> | |||
| :<math>C=4\pi\varepsilon_0R \,</math> | |||
| Example values of self capacitance are: | Example values of self capacitance are: | ||
| *for the top "plate" of a ], typically a sphere 20 cm in radius: 22.24 pF, | *for the top "plate" of a ], typically a sphere 20 cm in radius: 22.24 pF, | ||
| *the planet ]: about 710 |
*the planet ]: about 710 μF.<ref>{{cite book | last1 = Tipler | first1 = Paul | last2 = Mosca | first2 = Gene | title = Physics for Scientists and Engineers | publisher = Macmillan | year = 2004 | edition = 5th | page = 752 | isbn = 978-0-7167-0810-0 }}</ref> | ||
| The inter-winding capacitance of a ] is sometimes called self capacitance,<ref>{{cite journal|title=Self capacitance of inductors|doi=10.1109/63.602562 | |
The inter-winding capacitance of a ] is sometimes called self capacitance,<ref>{{cite journal| title=Self capacitance of inductors|doi=10.1109/63.602562 |last1=Massarini |first1=A. |last2=Kazimierczuk |first2=M. K. |year=1997 |volume=12 |issue=4 |pages=671–676 |journal=IEEE Transactions on Power Electronics |postscript=: example of the use of the term 'self capacitance'.|bibcode=1997ITPE...12..671M |citeseerx=10.1.1.205.7356 }}</ref> but this is a different phenomenon. It is actually mutual capacitance between the individual turns of the coil and is a form of stray or ]. This self capacitance is an important consideration at high frequencies: it changes the ] of the coil and gives rise to parallel ]. In many applications this is an undesirable effect and sets an upper frequency limit for the correct operation of the circuit.{{citation needed|date=May 2017}} | ||
| ==Mutual capacitance== | ==Mutual capacitance== | ||
| {{Main article|Mutual capacitance}} | |||
| A common form is a parallel-plate ], which consists of two conductive plates insulated from each other, usually sandwiching a ] material. In a parallel plate capacitor, capacitance is very nearly proportional to the surface area of the conductor plates and inversely proportional to the separation distance between the plates. | A common form is a parallel-plate ], which consists of two conductive plates insulated from each other, usually sandwiching a ] material. In a parallel plate capacitor, capacitance is very nearly proportional to the surface area of the conductor plates and inversely proportional to the separation distance between the plates. | ||
| If the charges on the plates are + |
If the charges on the plates are <math display="inline">+q</math> and <math display="inline">-q</math>, and <math display="inline">V</math> gives the ] between the plates, then the capacitance <math display="inline">C</math> is given by <math display="block">C = \frac{q}{V},</math> | ||
| :<math>C = \frac{q}{V}.</math> | |||
| which gives the voltage/] relationship | which gives the voltage/] relationship | ||
| <math display="block">i(t) = C \frac{dv(t)}{dt} + V\frac{dC}{dt},</math> | |||
| where <big><math display="inline">\frac{dv(t)}{dt}</math></big> is the instantaneous rate of change of voltage, and <big><math display="inline">\frac{dC}{dt}</math></big> is the instantaneous rate of change of the capacitance. For most applications, the change in capacitance over time is negligible, so the formula reduces to: | |||
| <math display="block">i(t) = C \frac{dv(t)}{dt},</math> | |||
| The energy stored in a capacitor is found by ] the work |
The energy stored in a capacitor is found by ] the work <math display="inline">W</math>: | ||
| <math display="block"> W_\text{charging} = \frac{1}{2}CV^2.</math> | |||
| :<math> W_\text{charging} = \frac{1}{2}CV^2</math> | |||
| ===Capacitance matrix=== | ===Capacitance matrix=== | ||
| The discussion above is limited to the case of two conducting plates, although of arbitrary size and shape. The definition <math>C = Q/V</math> does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case, ] introduced his '']''. If three (nearly ideal) conductors are given charges <math>Q_1, Q_2, Q_3</math>, then the voltage at conductor 1 is given by | |||
| <math display="block">V_1 = P_{11}Q_1 + P_{12} Q_2 + P_{13}Q_3, </math> | |||
| and similarly for the other voltages. ] and ] showed that the coefficients of potential are symmetric, so that <math>P_{12} = P_{21}</math>, etc. Thus the system can be described by a collection of coefficients known as the ''elastance matrix'' or ''reciprocal capacitance matrix'', which is defined as: | |||
| <math display="block">P_{ij} = \frac{\partial V_{i}}{\partial Q_{j}}.</math> | |||
| From this, the mutual capacitance <math>C_{m}</math> between two objects can be defined<ref name=Jackson1999>{{cite book |last=Jackson |first=John David |title=Classical Electrodynamic |publisher=John Wiley & Sons |year=1999 |edition=3rd |page=43 |isbn=978-0-471-30932-1}}</ref> by solving for the total charge <math display="inline">Q</math> and using <math>C_{m}=Q/V</math>. | |||
| The discussion above is limited to the case of two conducting plates, although of arbitrary size and shape. | |||
| The definition | |||
| <math>C = Q/V</math> does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case, Maxwell introduced his '']''. If three (nearly ideal) conductors are given charges <math>Q_1, Q_2, Q_3</math>, then the voltage at conductor 1 is given by | |||
| <math display="block">C_m = \frac{1}{(P_{11} + P_{22})-(P_{12} + P_{21})}.</math> | |||
| Since no actual device holds perfectly equal and opposite charges on each of the two "plates", it is the mutual capacitance that is reported on capacitors. | |||
| and similarly for the other voltages. ] and ] showed that the coefficients of potential are symmetric, so that <math>P_{12}=P_{21}</math>, etc. Thus the system can be described by a collection of coefficients known as the ''elastance matrix'' or ''reciprocal capacitance matrix'', which is defined as: | |||
| The collection of coefficients <math>C_{ij} = \frac{\partial Q_{i}}{\partial V_{j}}</math> is known as the ''capacitance matrix'',<ref name=maxwell>{{cite book| last =Maxwell | first =James | author-link =James Clerk Maxwell | title = A treatise on electricity and magnetism |volume=1 | publisher = Clarendon Press | year = 1873 | chapter =3 | at =p. 88ff | chapter-url = https://archive.org/details/electricandmagne01maxwrich}}</ref><ref>{{Cite web |title=Capacitance: Charge as a Function of Voltage |url=http://www.av8n.com/physics/capacitance.htm |website=Av8n.com |access-date=20 September 2010}}</ref><ref>{{cite journal |last1= Smolić |first1= Ivica |last2= Klajn |first2= Bruno |date= 2021 |title= Capacitance matrix revisited |url= https://www.jpier.org/PIERB/pier.php?paper=21011501 |journal= Progress in Electromagnetics Research B |volume= 92 |pages= 1–18 |doi= 10.2528/PIERB21011501|arxiv=2007.10251 |access-date= 4 May 2021|doi-access= free }}</ref> and is the ] of the elastance matrix. | |||
| :<math>P_{ij} = \frac{\partial V_{i}}{\partial Q_{j}}</math> | |||
| ==Capacitors== | |||
| From this, the mutual capacitance <math>C_{m}</math> between two objects can be defined<ref name=Jackson1999>{{cite book |last=Jackson |first=John David |title=Classical Electrodynamic |publisher=John Wiley & Sons |year=1999 |edition=3rd |page=43 |isbn=978-0-471-30932-1}}</ref> by solving for the total charge ''Q'' and using <math>C_{m}=Q/V</math>. | |||
| {{Main|Capacitor}} | |||
| The capacitance of the majority of capacitors used in electronic circuits is generally several orders of magnitude smaller than the ]. The most common units of capacitance are the ]farad (μF), ]farad (nF), ]farad (pF), and, in microcircuits, ]farad (fF). Some applications also use ] that can be much larger, as much as hundreds of farads, and parasitic capacitive elements can be less than a femtofarad. Historical texts use other, obsolete submultiples of the farad, such as "mf" and "mfd" for microfarad (μF); "mmf", "mmfd", "pfd", "μμF" for picofarad (pF).<ref>{{cite web |url=http://www.justradios.com/MFMMFD.html |title=Capacitor MF-MMFD Conversion Chart |website=Just Radios}}</ref><ref>{{cite book |url=https://archive.org/details/FundamentalsOfElectronics93400A1b |title=Fundamentals of Electronics |volume=1b – Basic Electricity – Alternating Current |publisher=Bureau of Naval Personnel |year=1965 |page=}}</ref> | |||
| The capacitance can be calculated if the geometry of the conductors and the dielectric properties of the insulator between the conductors are known. Capacitance is proportional to the area of overlap and inversely proportional to the separation between conducting sheets. The closer the sheets are to each other, the greater the capacitance. | |||
| : <math>C_m = \frac{1}{(P_{11} + P_{22})-(P_{12} + P_{21})}</math> | |||
| An example is the capacitance of a capacitor constructed of two parallel plates both of area <math display="inline">A</math> separated by a distance <math display="inline">d</math>. If <math display="inline">d</math> is sufficiently small with respect to the smallest chord of <math display="inline">A</math>, there holds, to a high level of accuracy: | |||
| Since no actual device holds perfectly equal and opposite charges on each of the two "plates", it is the mutual capacitance that is reported on capacitors. | |||
| <math display="block">\ C=\varepsilon\frac{A}{d};</math> | |||
| <math display="block">\varepsilon=\varepsilon_0 \varepsilon_r,</math> | |||
| The collection of coefficients <math>C_{ij} =\frac{\partial Q_{i}}{\partial V_{j}}</math> is known as the ''capacitance matrix'',<ref name=maxwell>{{cite book| last =Maxwell | first =James | author-link =James Clerk Maxwell | title = A treatise on electricity and magnetism |volume=1 | publisher = Clarendon Press | year = 1873 | chapter =3 | at =p. 88ff | chapter-url = https://archive.org/details/electricandmagne01maxwrich}}</ref><ref>{{Cite web |title=Capacitance : Charge as a Function of Voltage |url=http://www.av8n.com/physics/capacitance.htm |website=Av8n.com |accessdate=20 September 2010}}</ref> and is the ] of the elastance matrix. | |||
| ==Capacitors== | |||
| {{Main article|Capacitor}} | |||
| The capacitance of the majority of capacitors used in electronic circuits is generally several orders of magnitude smaller than the ]. The most common subunits of capacitance in use today are the ]farad (µF), ]farad (nF), ]farad (pF), and, in microcircuits, ]farad (fF). However, specially made ] can be much larger (as much as hundreds of farads), and parasitic capacitive elements can be less than a femtofarad. In the past, alternate subunits were used in historical electronic books; "mfd" and "mf" for microfarad (µF); "mmfd", "mmf", "µµF" for picofarad (pF); but are rarely used any more.<ref>{{cite web |url=http://www.justradios.com/MFMMFD.html |title=Capacitor MF-MMFD Conversion Chart |website=Just Radios}}</ref><ref>{{cite book |url=https://archive.org/details/FundamentalsOfElectronics93400A1b |title=Fundamentals of Electronics |volume=Volume 1b — Basic Electricity — Alternating Current |publisher=Bureau of Naval Personnel |year=1965 |page=197}}</ref> | |||
| Capacitance can be calculated if the geometry of the conductors and the dielectric properties of the insulator between the conductors are known. A qualitative explanation for this can be given as follows.<br> Once a positive charge is put unto a conductor, this charge creates an electrical field, repelling any other positive charge to be moved onto the conductor; i.e., increasing the necessary voltage. But if nearby there is another conductor with a negative charge on it, the electrical field of the positive conductor repelling the second positive charge is weakened (the second positive charge also feels the attracting force of the negative charge). So due to the second conductor with a negative charge, it becomes easier to put a positive charge on the already positive charged first conductor, and vice versa; i.e., the necessary voltage is lowered. <br> As a quantitative example consider the capacitance of a capacitor constructed of two parallel plates both of area ''A'' separated by a distance ''d''. If ''d'' is sufficiently small with respect to the smallest chord of ''A'', there holds, to a high level of accuracy: | |||
| :<math>\ C=\varepsilon_0\frac{A}{d}</math> | |||
| where | where | ||
| *<math display="inline">C</math> is the capacitance, in farads; | |||
| *<math display="inline">A</math> is the area of overlap of the two plates, in square meters; | |||
| *<math display="inline">\varepsilon_0</math> is the ] {{nowrap|(<math display="inline">\varepsilon_0 \approx 8.854\times 10^{-12} ~ \mathrm{F{\cdot}m^{-1}}</math>);}} | |||
| *<math display="inline">\varepsilon_r</math> is the ] (also dielectric constant) of the material in between the plates {{nowrap|(<math display="inline">\varepsilon_r \approx 1</math>}} for air); and | |||
| :''d'' is the separation between the plates, in meters; | |||
| *<math display="inline">d</math> is the separation between the plates, in meters. | |||
| Capacitance is proportional to the area of overlap and inversely proportional to the separation between conducting sheets. The closer the sheets are to each other, the greater the capacitance. | |||
| The equation is a good approximation if ''d'' is small compared to the other dimensions of the plates so that the electric field in the capacitor area is uniform, and the so-called ''fringing field'' around the periphery provides only a small contribution to the capacitance. | The equation is a good approximation if ''d'' is small compared to the other dimensions of the plates so that the electric field in the capacitor area is uniform, and the so-called ''fringing field'' around the periphery provides only a small contribution to the capacitance. | ||
| Combining the equation for capacitance with the above equation for the energy stored in a |
Combining the equation for capacitance with the above equation for the energy stored in a capacitor, for a flat-plate capacitor the energy stored is: | ||
| <math display="block"> W_\text{stored} = \frac{1}{2} C V^2 = \frac{1}{2} \varepsilon \frac{A}{d} V^2.</math> | |||
| where <math display="inline">W</math> is the energy, in joules; <math display="inline">C</math> is the capacitance, in farads; and <math display="inline">V</math> is the voltage, in volts. | |||
| :<math> W_\text{stored} = \frac{1}{2} C V^2 = \frac{1}{2} \varepsilon_{0} \frac{A}{d} V^2.</math> | |||
| where ''W'' is the energy, in joules; ''C'' is the capacitance, in farads; and ''V'' is the voltage, in volts. | |||
| ==Stray capacitance== | ==Stray capacitance== | ||
| {{Main |
{{Main|Parasitic capacitance}} | ||
| Any two adjacent conductors can function as a capacitor, though the capacitance is small unless the conductors are close together for long distances or over a large area. This (often unwanted) capacitance is called parasitic or |
Any two adjacent conductors can function as a capacitor, though the capacitance is small unless the conductors are close together for long distances or over a large area. This (often unwanted) capacitance is called parasitic or stray capacitance. Stray capacitance can allow signals to leak between otherwise isolated circuits (an effect called ]), and it can be a limiting factor for proper functioning of circuits at ]. | ||
| Stray capacitance between the input and output in amplifier circuits can be troublesome because it can form a path for ], which can cause instability and ] in the amplifier. It is often convenient for analytical purposes to replace this capacitance with a combination of one input-to-ground capacitance and one output-to-ground capacitance; the original configuration |
Stray capacitance between the input and output in amplifier circuits can be troublesome because it can form a path for ], which can cause instability and ] in the amplifier. It is often convenient for analytical purposes to replace this capacitance with a combination of one input-to-ground capacitance and one output-to-ground capacitance; the original configuration – including the input-to-output capacitance – is often referred to as a pi-configuration. Miller's theorem can be used to effect this replacement: it states that, if the gain ratio of two nodes is {{sfrac|1|''K''}}, then an ] of ''Z'' connecting the two nodes can be replaced with a {{sfrac|''Z''|1 − ''K''}} impedance between the first node and ground and a {{sfrac|''KZ''|''K'' − 1}} impedance between the second node and ground. Since impedance varies inversely with capacitance, the internode capacitance, ''C'', is replaced by a capacitance of KC from input to ground and a capacitance of {{sfrac|(''K'' − 1)''C''|''K''}} from output to ground. When the input-to-output gain is very large, the equivalent input-to-ground impedance is very small while the output-to-ground impedance is essentially equal to the original (input-to-output) impedance. | ||
| ==Capacitance of conductors with simple shapes == | ==Capacitance of conductors with simple shapes == | ||
| Calculating the capacitance of a system amounts to solving the ] |
Calculating the capacitance of a system amounts to solving the ] <math display="inline">\nabla^2\varphi=0</math> with a constant potential <math display="inline">\varphi</math> on the 2-dimensional surface of the conductors embedded in 3-space. This is simplified by symmetries. There is no solution in terms of elementary functions in more complicated cases. | ||
| For plane situations analytic functions may be used to map different geometries to each other. See also ]. | For plane situations, analytic functions may be used to map different geometries to each other. See also ]. | ||
| {| class="wikitable" | {| class="wikitable" | ||
| |+ Capacitance of simple systems | |+ Capacitance of simple systems | ||
| ! Type !! Capacitance !! |
! Type !! Capacitance !! Diagram and definitions | ||
| |- | |- | ||
| ! Parallel-plate capacitor | ! Parallel-plate capacitor | ||
| | <math> \varepsilon A |
| <math>\ \mathcal{C} = \frac{\ \varepsilon A\ }{d}\ </math> | ||
| | ] | | ] | ||
| *<math display="inline">\varepsilon</math>: ] | |||
| |- | |- | ||
| ! Concentric cylinders | ! Concentric cylinders | ||
| | <math> \frac{2\pi \varepsilon \ell}{\ln \left( R_{2}/R_{1}\right) } </math> | | <math>\ \mathcal{C} = \frac{2\pi \varepsilon \ell}{\ \ln \left( R_{2}/R_{1}\right)\ }\ </math> | ||
| | ] | | ] | ||
| *<math display="inline">\varepsilon</math>: ] | |||
| |- | |- | ||
| ! Eccentric cylinders<ref>{{cite journal |last=Dawes |year=1973 |first=Chester L. |title=Capacitance and potential gradients of eccentric cylindrical condensers |doi=10.1063/1.1745162 |journal=Physics |volume=4 |issue=2 |pages=81–85 |url=https://aip.scitation.org/doi/abs/10.1063/1.1745162}}</ref> | |||
| ! Pair of parallel wires<ref name="Jackson 1975 80">{{Cite book|last=Jackson |first=J. D. |title=Classical Electrodynamics |year=1975|publisher=Wiley |page=80}}</ref> | |||
| | <math>\ |
| <big><math>\ \mathcal{C} = \frac{2\pi \varepsilon \ell}{\ \operatorname{arcosh}\left(\frac{R_{1}^2 + R_{2}^2 - d^2}{2 R_{1} R_{2}}\right)\ }\ </math></big> | ||
| |] | | ] | ||
| *<math display="inline">\varepsilon</math>: ] | |||
| *<math display="inline">R_1</math>: Outer radius | |||
| *<math display="inline">R_2</math>: Inner radius | |||
| *<math display="inline">d</math>: Distance between center | |||
| *<math display="inline">\ell</math>: Wire length | |||
| |- | |||
| ! Pair of parallel wires<ref name="Jackson 1975 80">{{cite book |last=Jackson |first=J. D. |year=1975 |title=Classical Electrodynamics |publisher=Wiley |page=80}}</ref> | |||
| | <big><math>\ \mathcal{C} = \frac{\pi \varepsilon \ell}{\ \operatorname{arcosh}\left( \frac{d}{2a}\right)\ } = \frac{\pi \varepsilon \ell}{\ \ln \left( \frac{d}{\ 2a\ } + \sqrt{\frac{d^2}{\ 4a^2\ } -1\ }\right)\ }\ </math></big> | |||
| |] | |||
| |- | |- | ||
| ! Wire parallel to wall<ref name="Jackson 1975 80"/> | ! Wire parallel to wall<ref name="Jackson 1975 80"/> | ||
| | <math>\frac{2\pi \varepsilon \ell}{\operatorname{arcosh}\left( \frac{d}{a}\right) }=\frac{2\pi \varepsilon \ell}{\ln \left( \frac{d}{a}+\sqrt{\frac{d^ |
| <big><math>\ \mathcal{C} = \frac{2\pi \varepsilon \ell}{\ \operatorname{arcosh}\left( \frac{d}{a}\right)\ } = \frac{2\pi \varepsilon \ell}{\ \ln \left( \frac{\ d\ }{a}+\sqrt{\frac{\ d^2\ }{a^2} - 1\ }\right)\ }\ </math></big> | ||
| | | |||
| | ''a'': Wire radius <br/>''d'': Distance, ''d > a'' <br/>''ℓ'': Wire length | |||
| *<math display="inline">a</math>: Wire radius | |||
| *<math display="inline">d</math>: Distance, <math display="inline">d > a</math> | |||
| *<math display="inline">\ell</math>: Wire length | |||
| |- | |- | ||
| ! Two parallel<br/>coplanar strips<ref>{{ |
! Two parallel<br/>coplanar strips<ref>{{cite book | last1 = Binns | last2 = Lawrenson | year = 1973 | title = Analysis and computation of electric and magnetic field problems | publisher = Pergamon Press | isbn = 978-0-08-016638-4}}<!--| access-date = 4 June 2010 --></ref> | ||
| | <math>\varepsilon \ell \frac{ K\left( \sqrt{1-k^ |
| <math>\ \mathcal{C} = \varepsilon \ell\ \frac{\ K\left( \sqrt{1-k^2\ } \right)\ }{ K\left( k \right) }\ </math> | ||
| | | |||
| | ''d'': Distance<br/>''w<sub>1</sub>, w<sub>2</sub>'': Strip width<br/>''k<sub>m</sub>'': ''d/(2w<sub>m</sub>+d)''<br/> | |||
| *<math display="inline">d</math>: Distance | |||
| ''k<sup>2</sup>'': ''k<sub>1</sub>k<sub>2</sub>''<br/>''K'': ]<br/>''ℓ'': Length | |||
| *<math display="inline">\ell</math>: Length | |||
| *<math display="inline">w_1, w_2</math>: Strip width | |||
| *<math display="inline">\ k_1 = \left( \tfrac{\ 2 w_1\ }{d} + 1 \right)^{-1}\ </math><br/><math>\ k_2 = \left( \tfrac{\ 2 w_2\ }{d} + 1 \right)^{-1}\ </math><math>\ k = \sqrt{ k_1\ k_2\ }\ </math> | |||
| *<math display="inline">K</math>: ] | |||
| |- | |- | ||
| ! Concentric spheres | ! Concentric spheres | ||
| | <math> \frac{4\pi \varepsilon}{\frac{1}{R_1}-\frac{1}{R_2}} </math> | | <math>\ \mathcal{C} = \frac{4\pi \varepsilon}{\ \frac{1}{R_1} - \frac{1}{R_2}\ }\ </math> | ||
| | ] | | ] | ||
| *<math display="inline">\varepsilon</math>: ] | |||
| |- | |- | ||
| ! Two spheres,<br/>equal radius<ref name="Maxwell 1873 266 ff">{{Cite book|last=Maxwell |first=J. |
! Two spheres,<br/>equal radius<ref name="Maxwell 1873 266 ff">{{Cite book |last=Maxwell |first=J.;C. |year=1873 |title=A Treatise on Electricity and Magnetism |publisher=Dover |page=266 ff |isbn=978-0-486-60637-8}}</ref><ref>{{Cite journal |last=Rawlins |first=A.D. |year=1985 |title=Note on the capacitance of two closely separated spheres |journal=IMA Journal of Applied Mathematics |volume=34 |issue=1 |pages=119–120 |doi=10.1093/imamat/34.1.119}}</ref> | ||
| | <math>\begin{align} | |||
| | <math>2\pi \varepsilon a\sum_{n=1}^{\infty }\frac{\sinh \left( \ln \left( D+\sqrt{D^2-1}\right) \right) }{\sinh \left( n\ln \left( D+\sqrt{ D^2-1}\right) \right) } </math><br/><math>=2\pi \varepsilon a\left\{ 1+\frac{1}{2D}+\frac{1}{4D^2}+\frac{1}{8D^{3}}+\frac{1}{8D^{4}}+\frac{3}{32D^{5}}+O\left( \frac{1}{D^{6}}\right) \right\}</math><br/><math>=2\pi \varepsilon a\left\{ \ln 2+\gamma -\frac{1}{2}\ln \left( 2D-2\right) +O\left( 2D-2\right) \right\}</math> | |||
| \ \mathcal{C}\ = &\ {} 2 \pi \varepsilon a\ \sum_{n=1}^{\infty }\frac{\sinh \left( \ln \left( D+\sqrt{D^2-1}\right) \right) }{\sinh \left( n\ln \left( D+\sqrt{ D^2-1}\right) \right) } \\ | |||
| | ''a'': Radius<br/>''d'': Distance, ''d'' > 2''a''<br/>''D'' = ''d''/2''a'', ''D'' > 1<br/> ''γ'': ] | |||
| ={}&{}2\pi \varepsilon a\left \\ | |||
| ={}&{} 2\pi \varepsilon a\left \\ | |||
| ={}&{} 2\pi \varepsilon a \,\frac{\sqrt{D^2 - 1}}{\log(q)}\left | |||
| \end{align}\ </math> | |||
| | | |||
| *<math display="inline">a</math>: Radius | |||
| *<math display="inline">d</math>: Distance, <math display="inline">d > 2a</math> | |||
| *<math display="inline">D = d/2a, D > 1</math> | |||
| *<math display="inline">\gamma</math>: ] | |||
| *<math>q = D + \sqrt{D^2 - 1}</math> | |||
| *<math>\psi_q(z)=\frac{\partial_z\Gamma_q(z)}{\Gamma_q(z)}</math>: the q-digamma function | |||
| *<math>\Gamma_q(z)</math>: the ]<ref>{{Cite book| last1 = Gasper | last2 = Rahman | title = Basic Hypergeometric Series | year = 2004 | publisher = Cambridge University Press |at = p.20-22 | isbn = 978-0-521-83357-8}}</ref> | |||
| See also ]. | |||
| |- | |- | ||
| ! Sphere in front of wall<ref name="Maxwell 1873 266 ff"/> | ! Sphere in front of wall<ref name="Maxwell 1873 266 ff"/> | ||
| | <math>4\pi \varepsilon a\sum_{n=1}^{\infty }\frac{\sinh \left( \ln \left( D+\sqrt{D^{2}-1}\right) \right) }{\sinh \left( n\ln \left( D+\sqrt{ D^{2}-1}\right) \right) } </math> | | <math>\ \mathcal{C} = 4\pi \varepsilon a\sum_{n=1}^{\infty }\frac{\sinh \left( \ln \left( D+\sqrt{D^{2}-1}\right) \right) }{\sinh \left( n\ln \left( D+\sqrt{ D^{2}-1}\right) \right) }\ </math> | ||
| | | |||
| | <math>a</math>: Radius<br/><math>d</math>: Distance, <math>d > a</math><br/><math>D=d/a</math> | |||
| *<math>\ a\ </math>: Radius | |||
| *<math>\ d\ </math>: Distance, <math>d > a</math> | |||
| *<math>D=d/a</math> | |||
| |- | |- | ||
| ! Sphere | ! Sphere | ||
| | <math> 4\pi \varepsilon a </math> | | <math>\ \mathcal{C} = 4 \pi \varepsilon a\ </math> | ||
| | | |||
| | <math>a</math>: Radius | |||
| *<math>a</math>: Radius | |||
| |- | |- | ||
| ! Circular disc<ref name="Jackson 1975 128">{{ |
! Circular disc<ref name="Jackson 1975 128">{{cite book |last=Jackson |first=J.D. |year=1975 |title=Classical Electrodynamics |publisher=Wiley |page=128, problem 3.3 }}</ref> | ||
| | <math> 8\varepsilon a </math> | | <math>\ \mathcal{C} = 8 \varepsilon a\ </math> | ||
| | | |||
| | <math>a</math>: Radius | |||
| * <math>a</math>: Radius | |||
| |- | |- | ||
| ! Thin straight wire,<br/> finite length<ref>{{ |
! Thin straight wire,<br/> finite length<ref>{{cite journal |last=Maxwell |first=J. C. |year=1878 |title=On the electrical capacity of a long narrow cylinder and of a disk of sensible thickness |journal=Proceedings of the London Mathematical Society |volume=IX |pages=94–101 |doi=10.1112/plms/s1-9.1.94 |url=https://zenodo.org/record/1447764 }}</ref><ref>{{Cite journal |last=Vainshtein |first=L. A. |year=1962 |title=Static boundary problems for a hollow cylinder of finite length. III Approximate formulas |journal=] |volume=32 |pages=1165–1173}}</ref><ref>{{cite journal |last=Jackson |first=J. D. |year=2000 |title=Charge density on thin straight wire, revisited |journal=American Journal of Physics |volume=68 |issue=9 |pages=789–799 |doi=10.1119/1.1302908 |bibcode = 2000AmJPh..68..789J }}</ref> | ||
| | <math> \frac{2\pi \varepsilon \ell}{\Lambda }\left |
| <math>\ \mathcal{C} = \frac{2\pi \varepsilon \ell}{\Lambda }\left\ </math> | ||
| | | |||
| | <math>a</math>: Wire radius<br><math>\ell</math>: Length<br/><math>\Lambda = \ln \left( \ell/a \right)</math> | |||
| *<math>a</math>: Wire radius | |||
| *<math>\ell</math>: Length | |||
| *<math>\ \Lambda = \ln \left( \ell/a \right)\ </math> | |||
| |} | |} | ||
| ==Energy storage== | ==Energy storage== | ||
| The ] (measured in ]s) stored in a capacitor is equal to the ''work'' required to push the charges into the capacitor, i.e. to charge it. Consider a capacitor of capacitance ''C'', holding a charge +''q'' on one plate and −''q'' on the other. Moving a small element of charge d''q'' from one plate to the other against the potential difference {{nowrap|''V'' |
The ] (measured in ]s) stored in a capacitor is equal to the ''work'' required to push the charges into the capacitor, i.e. to charge it. Consider a capacitor of capacitance ''C'', holding a charge +''q'' on one plate and −''q'' on the other. Moving a small element of charge d''q'' from one plate to the other against the potential difference {{nowrap|1=''V'' = ''q''/''C''}} requires the work d''W'': | ||
| <math display="block"> \mathrm{d}W = \frac{q}{C}\,\mathrm{d}q,</math> | |||
| :<math> \mathrm{d}W = \frac{q}{C}\,\mathrm{d}q </math> | |||
| where ''W'' is the work measured in joules, ''q'' is the charge measured in coulombs and ''C'' is the capacitance, measured in farads. | where ''W'' is the work measured in joules, ''q'' is the charge measured in coulombs and ''C'' is the capacitance, measured in farads. | ||
| The energy stored in a capacitor is found by ] this equation. Starting with an uncharged capacitance ({{nowrap|''q'' |
The energy stored in a capacitor is found by ] this equation. Starting with an uncharged capacitance ({{nowrap|1=''q'' = 0}}) and moving charge from one plate to the other until the plates have charge +''Q'' and −''Q'' requires the work ''W'': | ||
| <math display="block"> W_\text{charging} = \int_0^Q \frac{q}{C} \, \mathrm{d}q = \frac{1}{2}\frac{Q^2}{C} = \frac{1}{2}QV = \frac{1}{2}CV^2 = W_\text{stored}.</math> | |||
| :<math> W_\text{charging} = \int_0^Q \frac{q}{C} \, \mathrm{d}q = \frac{1}{2}\frac{Q^2}{C} = \frac{1}{2}QV = \frac{1}{2}CV^2 = W_\text{stored}.</math> | |||
| ==Nanoscale systems== | ==Nanoscale systems== | ||
| The capacitance of nanoscale dielectric capacitors such as ] may differ from conventional formulations of larger capacitors. In particular, the electrostatic potential difference experienced by electrons in conventional capacitors is spatially well-defined and fixed by the shape and size of metallic electrodes in addition to the statistically large number of electrons present in conventional capacitors. In nanoscale capacitors, however, the electrostatic potentials experienced by electrons are determined by the number and locations of all electrons that contribute to the electronic properties of the device. In such devices, the number of electrons may be very small, |
The capacitance of nanoscale dielectric capacitors such as ] may differ from conventional formulations of larger capacitors. In particular, the electrostatic potential difference experienced by electrons in conventional capacitors is spatially well-defined and fixed by the shape and size of metallic electrodes in addition to the statistically large number of electrons present in conventional capacitors. In nanoscale capacitors, however, the electrostatic potentials experienced by electrons are determined by the number and locations of all electrons that contribute to the electronic properties of the device. In such devices, the number of electrons may be very small, so the resulting spatial distribution of equipotential surfaces within the device is exceedingly complex. | ||
| ===Single-electron devices=== | ===Single-electron devices=== | ||
| The capacitance of a connected, or "closed", single-electron device is twice the capacitance of an unconnected, or "open", single-electron device.<ref name= Tsu>{{Cite book | pages=312–315 | title=Superlattice to Nanoelectronics | isbn = 978-0-08-096813-1 | author=Raphael Tsu | publisher=Elsevier | year=2011 }}</ref> This fact may be traced more fundamentally to the energy stored in the single-electron device whose "direct polarization" interaction energy may be equally divided into the interaction of the electron with the polarized charge on the device itself due to the presence of the electron and the amount of potential energy required to form the polarized charge on the device (the interaction of charges in the device's dielectric material with the potential due to the electron).<ref name= LaFave-DCD>{{Cite journal | author=T. LaFave Jr. | title=Discrete charge dielectric model of electrostatic energy | arxiv=1203.3798|journal=J. Electrostatics | year=2011 | volume=69 | issue=6 | pages=414–418 | doi=10.1016/j.elstat.2011.06.006 | s2cid=94822190 }}</ref> | |||
| The capacitance of a connected, or "closed", single-electron device is twice the capacitance of an unconnected, or "open", single-electron device.<ref name= Tsu> | |||
| {{Cite book | |||
| |pages=312–315 | |||
| |title=Superlattice to Nanoelectronics | |||
| |isbn=978-0-08-096813-1 | |||
| |author=Raphael Tsu | |||
| |publisher=Elsevier | |||
| |year=2011 | |||
| }}</ref> This fact may be traced more fundamentally to the energy stored in the single-electron device whose "direct polarization" interaction energy may be equally divided into the interaction of the electron with the polarized charge on the device itself due to the presence of the electron and the amount of potential energy required to form the polarized charge on the device (the interaction of charges in the device's dielectric material with the potential due to the electron).<ref name= LaFave-DCD> | |||
| {{Cite journal | |||
| |author=T. LaFave Jr. | |||
| |title=Discrete charge dielectric model of electrostatic energy | |||
| |arxiv=1203.3798|journal=J. Electrostatics | |||
| |year=2011 | |||
| |volume=69 | |||
| |issue=6 | |||
| |pages=414–418 | |||
| |doi=10.1016/j.elstat.2011.06.006 | |||
| }}</ref> | |||
| ===Few-electron devices=== | ===Few-electron devices=== | ||
| The derivation of a "quantum capacitance" of a few-electron device involves the thermodynamic chemical potential of an ''N''-particle system given by | The derivation of a "quantum capacitance" of a few-electron device involves the thermodynamic chemical potential of an ''N''-particle system given by | ||
| <math display="block">\mu(N) = U(N) - U(N-1),</math> | |||
| :<math>\mu(N) = U(N) - U(N-1)</math> | |||
| whose energy terms may be obtained as solutions of the Schrödinger equation. The definition of capacitance, | whose energy terms may be obtained as solutions of the Schrödinger equation. The definition of capacitance, | ||
| <math display="block">{1\over C} \equiv {\Delta V\over\Delta Q},</math> | |||
| :<math>{1\over C} \equiv {\Delta \,V\over\Delta \,Q}</math>, | |||
| with the potential difference | with the potential difference | ||
| <math display="block">\Delta V = {\Delta \mu \,\over e} = {\mu(N + \Delta N) -\mu(N) \over e}</math> | |||
| :<math>\Delta \,V = {\Delta \,\mu \,\over e} = {\mu(N+\Delta \,N) -\mu(N) \over e}</math> | |||
| may be applied to the device with the addition or removal of individual electrons, | may be applied to the device with the addition or removal of individual electrons, | ||
| <math display="block">\Delta N = 1</math> and <math display="block">\Delta Q = e.</math> | |||
| The "quantum capacitance" of the device is then<ref>{{cite journal | |||
| :<math>\Delta \,N = 1</math> and <math>\Delta \,Q=e</math>. | |||
| Then | |||
| :<math>C_Q(N) = {e^2\over\mu(N+1)-\mu(N)} = {e^2 \over E(N)}</math> | |||
| is the "quantum capacitance" of the device.<ref> | |||
| {{cite journal | |||
| |author1=G. J. Iafrate |author2=K. Hess |author3=J. B. Krieger |author4=M. Macucci |year=1995 | |author1=G. J. Iafrate |author2=K. Hess |author3=J. B. Krieger |author4=M. Macucci |year=1995 | ||
| |title=Capacitive nature of atomic-sized structures | |title=Capacitive nature of atomic-sized structures | ||
| Line 228: | Line 228: | ||
| |issue=15 | |issue=15 | ||
| |pages=10737–10739 |doi=10.1103/physrevb.52.10737 | |pages=10737–10739 |doi=10.1103/physrevb.52.10737 | ||
| |bibcode = 1995PhRvB..5210737I }}</ref> | |pmid=9980157 |bibcode = 1995PhRvB..5210737I }}</ref> | ||
| <math display="block">C_Q(N) = \frac{e^2}{\mu(N+1)-\mu(N)} = \frac{e^2}{E(N)}.</math> | |||
| This expression of "quantum capacitance" may be written as | This expression of "quantum capacitance" may be written as | ||
| <math display="block">C_Q(N) = {e^2\over U(N)},</math> | |||
| :<math>C_Q(N) = {e^2\over U(N)}</math> | |||
| which differs from the conventional expression described in the introduction where <math>W_\text{stored} = U</math>, the stored electrostatic potential energy, | which differs from the conventional expression described in the introduction where <math>W_\text{stored} = U</math>, the stored electrostatic potential energy, | ||
| <math display="block">C = {Q^2\over 2U},</math> | |||
| by a factor of {{sfrac|2}} with <math>Q = Ne</math>. | |||
| However, within the framework of purely classical electrostatic interactions, the appearance of the factor of {{sfrac|2}} is the result of integration in the conventional formulation involving the work done when charging a capacitor, | |||
| :<math>C = {Q^2\over 2U}</math> | |||
| <math display="block"> W_\text{charging} = U = \int_0^Q \frac{q}{C} \, \mathrm{d}q,</math> | |||
| by a factor of 1/2 with <math>Q = Ne</math>. | |||
| However, within the framework of purely classical electrostatic interactions, the appearance of the factor of 1/2 is the result of integration in the conventional formulation, | |||
| :<math> W_\text{charging} = U = \int_0^Q \frac{q}{C} \, \mathrm{d}q</math> | |||
| which is appropriate since <math>\mathrm{d}q = 0</math> for systems involving either many electrons or metallic electrodes, but in few-electron systems, <math>\mathrm{d}q \to \Delta \,Q= e</math>. The integral generally becomes a summation. One may trivially combine the expressions of capacitance and electrostatic interaction energy, | |||
| :<math>Q=CV</math> and <math>U=QV</math>, | |||
| respectively, to obtain, | |||
| which is appropriate since <math>\mathrm{d}q = 0</math> for systems involving either many electrons or metallic electrodes, but in few-electron systems, <math>\mathrm{d}q \to \Delta \,Q= e</math>. The integral generally becomes a summation. One may trivially combine the expressions of capacitance | |||
| :<math>C = Q{1\over V} = Q {Q \over U} = {Q^2 \over U}</math> | |||
| <math display="block">Q=CV</math> | |||
| and electrostatic interaction energy, | |||
| <math display="block">U = Q V ,</math> | |||
| to obtain | |||
| <math display="block">C = Q{1\over V} = Q {Q \over U} = {Q^2 \over U},</math> | |||
| which is similar to the quantum capacitance. A more rigorous derivation is reported in the literature.<ref> | which is similar to the quantum capacitance. A more rigorous derivation is reported in the literature.<ref>{{cite journal | ||
| {{cite journal | |||
| |author1 = T. LaFave Jr | |author1 = T. LaFave Jr | ||
| |author2 = R. Tsu | |author2 = R. Tsu | ||
| | |
|date = March–April 2008 | ||
| |title = Capacitance: A property of nanoscale materials based on spatial symmetry of discrete electrons | |title = Capacitance: A property of nanoscale materials based on spatial symmetry of discrete electrons | ||
| |url = http://www.pagesofmind.com/FullTextPubs/La08-LaFave-2008-capacitance-a-property-of-nanoscale-materials.pdf | |url = http://www.pagesofmind.com/FullTextPubs/La08-LaFave-2008-capacitance-a-property-of-nanoscale-materials.pdf | ||
| | |
|access-date = 12 February 2014 | ||
| |journal = Microelectronics Journal | |journal = Microelectronics Journal | ||
| |volume = 39 | |volume = 39 | ||
| Line 265: | Line 259: | ||
| |pages = 617–623 | |pages = 617–623 | ||
| |doi = 10.1016/j.mejo.2007.07.105 | |doi = 10.1016/j.mejo.2007.07.105 | ||
| |url-status |
|url-status = dead | ||
| | |
|archive-url = https://web.archive.org/web/20140222131652/http://www.pagesofmind.com/FullTextPubs/La08-LaFave-2008-capacitance-a-property-of-nanoscale-materials.pdf | archive-date = 22 February 2014}}</ref> In particular, to circumvent the mathematical challenges of spatially complex equipotential surfaces within the device, an ''average'' electrostatic potential experienced by each electron is utilized in the derivation. | ||
| |archivedate = 22 February 2014 | |||
| |df = dmy-all | |||
| }}</ref> In particular, to circumvent the mathematical challenges of the spatially complex equipotential surfaces within the device, an ''average'' electrostatic potential experiences by ''each'' electron is utilized in the derivation. | |||
| Apparent mathematical differences may be understood more fundamentally. The potential energy, <math>U(N)</math>, of an isolated device (self-capacitance) is twice that stored in a "connected" device in the lower limit <math>N = 1</math>. As <math>N</math> grows large, <math>U(N)\to U</math>.<ref name=LaFave-DCD/> Thus, the general expression of capacitance is | |||
| <math display="block">C(N) = {(Ne)^2 \over U(N)}.</math> | |||
| In nanoscale devices such as quantum dots, the "capacitor" is often an isolated or partially isolated component within the device. The primary differences between nanoscale capacitors and macroscopic (conventional) capacitors are the number of excess electrons (charge carriers, or electrons, that contribute to the device's electronic behavior) and the shape and size of metallic electrodes. In nanoscale devices, ] consisting of metal atoms typically do not exhibit the same conductive properties as their macroscopic, or bulk material, counterparts. | |||
| :<math>C(N) = {(Ne)^2 \over U(N)}</math>. | |||
| In nanoscale devices such as quantum dots, the "capacitor" is often an isolated, or partially isolated, component within the device. The primary differences between nanoscale capacitors and macroscopic (conventional) capacitors are the number of excess electrons (charge carriers, or electrons, that contribute to the device's electronic behavior) and the shape and size of metallic electrodes. In nanoscale devices, ] consisting of metal atoms typically do not exhibit the same conductive properties as their macroscopic, or bulk material, counterparts. | |||
| ==Capacitance in electronic and semiconductor devices== | ==Capacitance in electronic and semiconductor devices== | ||
| In electronic and semiconductor devices, transient or frequency-dependent current between terminals contains both conduction and displacement components. Conduction current is related to moving charge carriers (electrons, holes, ions, etc.), while displacement current is caused by time-varying electric field. Carrier transport is affected by electric |
In electronic and semiconductor devices, transient or frequency-dependent current between terminals contains both conduction and displacement components. Conduction current is related to moving charge carriers (electrons, holes, ions, etc.), while displacement current is caused by a time-varying electric field. Carrier transport is affected by electric fields and by a number of physical phenomena - such as carrier drift and diffusion, trapping, injection, contact-related effects, impact ionization, etc. As a result, device ] is frequency-dependent, and a simple electrostatic formula for capacitance <math>C = q/V,</math> is not applicable. A more general definition of capacitance, encompassing electrostatic formula, is:<ref name=LauxCapacitance>{{cite journal |first=S.E. |last=Laux |title=Techniques for small-signal analysis of semiconductor devices |journal=IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems |volume=4 |issue=4 |pages=472–481 |doi=10.1109/TCAD.1985.1270145 |date=Oct 1985|s2cid=13058472 }}</ref> | ||
| <math display="block">C = \frac{\operatorname{Im}(Y(\omega))}{\omega} ,</math> | |||
| :<math>C = \frac{\operatorname{Im}(Y(\omega))}{\omega} ,</math> | |||
| where <math>Y(\omega)</math> is the device admittance, and <math>\omega</math> is the angular frequency. | where <math>Y(\omega)</math> is the device admittance, and <math>\omega</math> is the angular frequency. | ||
| In general |
In general, capacitance is a function of frequency. At high frequencies, capacitance approaches a constant value, equal to "geometric" capacitance, determined by the terminals' geometry and dielectric content in the device. | ||
| A paper by Steven Laux<ref name=LauxCapacitance /> presents a review of numerical techniques for capacitance calculation. In particular, capacitance can be calculated by a Fourier transform of a transient current in response to a step-like voltage excitation: | A paper by Steven Laux<ref name=LauxCapacitance /> presents a review of numerical techniques for capacitance calculation. In particular, capacitance can be calculated by a Fourier transform of a transient current in response to a step-like voltage excitation: | ||
| <math display="block">C(\omega) = \frac{1}{\Delta V} \int_0^\infty \cos (\omega t) dt.</math> | |||
| :<math>C(\omega) = 1/(\Delta V) \int_0^\infty cos(\omega t) dt.</math> | |||
| ==Negative capacitance in semiconductor devices== | ==Negative capacitance in semiconductor devices== | ||
| Usually, capacitance in semiconductor devices is positive. However, in some devices and under certain conditions (temperature, applied voltages, frequency, etc.), capacitance can become negative. Non-monotonic behavior of the transient current in response to a step-like excitation has been proposed as the mechanism of negative capacitance.<ref name=JonscherNegCap>{{cite journal |first=A.K. |last=Jonscher |title=The physical origin of negative capacitance |journal=J. Chem. Soc. Faraday Trans. II |volume=82 |pages=75–81 |doi=10.1039/F29868200075 |date=1986}}</ref> Negative capacitance has been demonstrated and explored in many different types of semiconductor devices.<ref>{{cite journal |first1=M. |last1=Ershov |first2=H.C. |last2=Liu |first3=L. |last3=Li |first4=M. |last4=Buchanan |first5=Z.R. |last5=Wasilewski |first6=A.K. |last6=Jonscher |title=Negative capacitance effect in semiconductor devices |journal=IEEE Trans. Electron Devices |volume=45 |issue=10 |pages=2196–2206 |date=Oct 1998 |doi=10.1109/16.725254|arxiv=cond-mat/9806145 |bibcode=1998ITED...45.2196E }}</ref> | Usually, capacitance in semiconductor devices is positive. However, in some devices and under certain conditions (temperature, applied voltages, frequency, etc.), capacitance can become negative. Non-monotonic behavior of the transient current in response to a step-like excitation has been proposed as the mechanism of negative capacitance.<ref name=JonscherNegCap>{{cite journal |first=A.K. |last=Jonscher |title=The physical origin of negative capacitance |journal=J. Chem. Soc. Faraday Trans. II |volume=82 |pages=75–81 |doi=10.1039/F29868200075 |date=1986}}</ref> Negative capacitance has been demonstrated and explored in many different types of semiconductor devices.<ref>{{cite journal |first1=M. |last1=Ershov |first2=H.C. |last2=Liu |first3=L. |last3=Li |first4=M. |last4=Buchanan |first5=Z.R. |last5=Wasilewski |first6=A.K. |last6=Jonscher |title=Negative capacitance effect in semiconductor devices |journal=IEEE Trans. Electron Devices |volume=45 |issue=10 |pages=2196–2206 |date=Oct 1998 |doi=10.1109/16.725254|arxiv=cond-mat/9806145 |bibcode=1998ITED...45.2196E |s2cid=204925581 }}</ref> | ||
| == Measuring capacitance == | == Measuring capacitance == | ||
| {{Main |
{{Main|Capacitance meter}} | ||
| A ] is a piece of ] used to measure capacitance, mainly of discrete ]s. For most purposes and in most cases the capacitor must be disconnected from ]. |
A ] is a piece of ] used to measure capacitance, mainly of discrete ]s. For most purposes and in most cases the capacitor must be disconnected from ]. | ||
| Many DVMs (]s) have a capacitance-measuring function. These usually operate by charging and discharging the ] with a known ] and measuring the rate of rise of the resulting ]; the slower the rate of rise, the larger the capacitance. DVMs can usually measure capacitance from ] to a few hundred microfarads, but wider ranges are not unusual. It is also possible to measure capacitance by passing a known ] ] through the device under test and measuring the resulting ]age across it (does not work for polarised capacitors). | Many DVMs (]s) have a capacitance-measuring function. These usually operate by charging and discharging the ] with a known ] and measuring the rate of rise of the resulting ]; the slower the rate of rise, the larger the capacitance. DVMs can usually measure capacitance from ] to a few hundred microfarads, but wider ranges are not unusual. It is also possible to measure capacitance by passing a known ] ] through the device under test and measuring the resulting ]age across it (does not work for polarised capacitors). | ||
| 2700A capacitance bridge]] | 2700A capacitance bridge]] | ||
| More sophisticated instruments use other techniques such as inserting the capacitor-under-test into a ]. By varying the values of the other legs in the bridge (so as to bring the bridge into balance), the value of the unknown capacitor is determined. This method of ''indirect'' use of measuring capacitance ensures greater precision. Through the use of ]s and other careful design techniques, these instruments can usually measure capacitors over a range from picofarads to farads. | More sophisticated instruments use other techniques such as inserting the capacitor-under-test into a ]. By varying the values of the other legs in the bridge (so as to bring the bridge into balance), the value of the unknown capacitor is determined. This method of ''indirect'' use of measuring capacitance ensures greater precision. Through the use of ]s and other careful design techniques, these instruments can usually measure capacitors over a range from picofarads to farads. | ||
| ==See also== | ==See also== | ||
| {{div col begin|colwidth=14em}} | |||
| *] | |||
| * ] | |||
| *] | |||
| * ] | |||
| *] | |||
| * ] | |||
| *] | |||
| *] | * ] | ||
| *] | * ] | ||
| *] | * ] | ||
| *] | * ] | ||
| {{div col end}} | |||
| *] | |||
| *] | |||
| *] | |||
| ==References== | ==References== | ||
| {{ |
{{reflist|25em}} | ||
| ==Further reading== | ==Further reading== | ||
| Line 326: | Line 311: | ||
| *Saslow, Wayne M.(2002). ''Electricity, Magnetism, and Light''. Thomson Learning. {{ISBN|0-12-619455-6}}. See Chapter 8, and especially pp. 255–259 for coefficients of potential. | *Saslow, Wayne M.(2002). ''Electricity, Magnetism, and Light''. Thomson Learning. {{ISBN|0-12-619455-6}}. See Chapter 8, and especially pp. 255–259 for coefficients of potential. | ||
| {{Refend}} | {{Refend}} | ||
| ==External links== | |||
| *{{Commonscatinline|Capacitance}} | |||
| {{Authority control}} | |||
| ] | ] | ||
| ] | ] | ||
| ] | |||
| ] | ] | ||
| ] | |||
Latest revision as of 16:53, 28 December 2024
Ability of a body to store an electrical charge For capacitance of blood vessels, see Compliance (physiology).
| Common symbols | C |
|---|---|
| SI unit | farad |
| Other units | μF, nF, pF |
| In SI base units | F = A s kg m |
| Derivations from other quantities | C = charge / voltage |
| Dimension |
Capacitance is the ability of an object to store electric charge. It is measured by the charge in response to a difference in electric potential, expressed as the ratio of those quantities. Commonly recognized are two closely related notions of capacitance: self capacitance and mutual capacitance. An object that can be electrically charged exhibits self capacitance, for which the electric potential is measured between the object and ground. Mutual capacitance is measured between two components, and is particularly important in the operation of the capacitor, an elementary linear electronic component designed to add capacitance to an electric circuit.
The capacitance between two conductors depends only on the geometry; the opposing surface area of the conductors and the distance between them; and the permittivity of any dielectric material between them. For many dielectric materials, the permittivity, and thus the capacitance, is independent of the potential difference between the conductors and the total charge on them.
The SI unit of capacitance is the farad (symbol: F), named after the English physicist Michael Faraday. A 1 farad capacitor, when charged with 1 coulomb of electrical charge, has a potential difference of 1 volt between its plates. The reciprocal of capacitance is called elastance.
Self capacitance
In discussing electrical circuits, the term capacitance is usually a shorthand for the mutual capacitance between two adjacent conductors, such as the two plates of a capacitor. However, every isolated conductor also exhibits capacitance, here called self capacitance. It is measured by the amount of electric charge that must be added to an isolated conductor to raise its electric potential by one unit of measurement, e.g., one volt. The reference point for this potential is a theoretical hollow conducting sphere, of infinite radius, with the conductor centered inside this sphere.
Self capacitance of a conductor is defined by the ratio of charge and electric potential: where
- is the charge held,
- is the electric potential,
- is the surface charge density,
- is an infinitesimal element of area on the surface of the conductor, over which the surface charge density is integrated,
- is the length from to a fixed point M on the conductor,
- is the vacuum permittivity.
Using this method, the self capacitance of a conducting sphere of radius in free space (i.e. far away from any other charge distributions) is:
Example values of self capacitance are:
- for the top "plate" of a van de Graaff generator, typically a sphere 20 cm in radius: 22.24 pF,
- the planet Earth: about 710 μF.
The inter-winding capacitance of a coil is sometimes called self capacitance, but this is a different phenomenon. It is actually mutual capacitance between the individual turns of the coil and is a form of stray or parasitic capacitance. This self capacitance is an important consideration at high frequencies: it changes the impedance of the coil and gives rise to parallel resonance. In many applications this is an undesirable effect and sets an upper frequency limit for the correct operation of the circuit.
Mutual capacitance
A common form is a parallel-plate capacitor, which consists of two conductive plates insulated from each other, usually sandwiching a dielectric material. In a parallel plate capacitor, capacitance is very nearly proportional to the surface area of the conductor plates and inversely proportional to the separation distance between the plates.
If the charges on the plates are and , and gives the voltage between the plates, then the capacitance is given by which gives the voltage/current relationship where is the instantaneous rate of change of voltage, and is the instantaneous rate of change of the capacitance. For most applications, the change in capacitance over time is negligible, so the formula reduces to:
The energy stored in a capacitor is found by integrating the work :
Capacitance matrix
The discussion above is limited to the case of two conducting plates, although of arbitrary size and shape. The definition does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case, James Clerk Maxwell introduced his coefficients of potential. If three (nearly ideal) conductors are given charges , then the voltage at conductor 1 is given by and similarly for the other voltages. Hermann von Helmholtz and Sir William Thomson showed that the coefficients of potential are symmetric, so that , etc. Thus the system can be described by a collection of coefficients known as the elastance matrix or reciprocal capacitance matrix, which is defined as:
From this, the mutual capacitance between two objects can be defined by solving for the total charge and using .
Since no actual device holds perfectly equal and opposite charges on each of the two "plates", it is the mutual capacitance that is reported on capacitors.
The collection of coefficients is known as the capacitance matrix, and is the inverse of the elastance matrix.
Capacitors
Main article: CapacitorThe capacitance of the majority of capacitors used in electronic circuits is generally several orders of magnitude smaller than the farad. The most common units of capacitance are the microfarad (μF), nanofarad (nF), picofarad (pF), and, in microcircuits, femtofarad (fF). Some applications also use supercapacitors that can be much larger, as much as hundreds of farads, and parasitic capacitive elements can be less than a femtofarad. Historical texts use other, obsolete submultiples of the farad, such as "mf" and "mfd" for microfarad (μF); "mmf", "mmfd", "pfd", "μμF" for picofarad (pF).
The capacitance can be calculated if the geometry of the conductors and the dielectric properties of the insulator between the conductors are known. Capacitance is proportional to the area of overlap and inversely proportional to the separation between conducting sheets. The closer the sheets are to each other, the greater the capacitance.
An example is the capacitance of a capacitor constructed of two parallel plates both of area separated by a distance . If is sufficiently small with respect to the smallest chord of , there holds, to a high level of accuracy:
where
- is the capacitance, in farads;
- is the area of overlap of the two plates, in square meters;
- is the electric constant ();
- is the relative permittivity (also dielectric constant) of the material in between the plates ( for air); and
- is the separation between the plates, in meters.
The equation is a good approximation if d is small compared to the other dimensions of the plates so that the electric field in the capacitor area is uniform, and the so-called fringing field around the periphery provides only a small contribution to the capacitance.
Combining the equation for capacitance with the above equation for the energy stored in a capacitor, for a flat-plate capacitor the energy stored is: where is the energy, in joules; is the capacitance, in farads; and is the voltage, in volts.
Stray capacitance
Main article: Parasitic capacitanceAny two adjacent conductors can function as a capacitor, though the capacitance is small unless the conductors are close together for long distances or over a large area. This (often unwanted) capacitance is called parasitic or stray capacitance. Stray capacitance can allow signals to leak between otherwise isolated circuits (an effect called crosstalk), and it can be a limiting factor for proper functioning of circuits at high frequency.
Stray capacitance between the input and output in amplifier circuits can be troublesome because it can form a path for feedback, which can cause instability and parasitic oscillation in the amplifier. It is often convenient for analytical purposes to replace this capacitance with a combination of one input-to-ground capacitance and one output-to-ground capacitance; the original configuration – including the input-to-output capacitance – is often referred to as a pi-configuration. Miller's theorem can be used to effect this replacement: it states that, if the gain ratio of two nodes is 1/K, then an impedance of Z connecting the two nodes can be replaced with a Z/1 − K impedance between the first node and ground and a KZ/K − 1 impedance between the second node and ground. Since impedance varies inversely with capacitance, the internode capacitance, C, is replaced by a capacitance of KC from input to ground and a capacitance of (K − 1)C/K from output to ground. When the input-to-output gain is very large, the equivalent input-to-ground impedance is very small while the output-to-ground impedance is essentially equal to the original (input-to-output) impedance.
Capacitance of conductors with simple shapes
Calculating the capacitance of a system amounts to solving the Laplace equation with a constant potential on the 2-dimensional surface of the conductors embedded in 3-space. This is simplified by symmetries. There is no solution in terms of elementary functions in more complicated cases.
For plane situations, analytic functions may be used to map different geometries to each other. See also Schwarz–Christoffel mapping.
| Type | Capacitance | Diagram and definitions |
|---|---|---|
| Parallel-plate capacitor | ||
| Concentric cylinders | 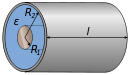
| |
| Eccentric cylinders | 
| |
| Pair of parallel wires | 
| |
| Wire parallel to wall |
| |
| Two parallel coplanar strips |
| |
| Concentric spheres | 
| |
| Two spheres, equal radius |
See also Basic hypergeometric series. | |
| Sphere in front of wall |
| |
| Sphere |
| |
| Circular disc |
| |
| Thin straight wire, finite length |
|
Energy storage
The energy (measured in joules) stored in a capacitor is equal to the work required to push the charges into the capacitor, i.e. to charge it. Consider a capacitor of capacitance C, holding a charge +q on one plate and −q on the other. Moving a small element of charge dq from one plate to the other against the potential difference V = q/C requires the work dW: where W is the work measured in joules, q is the charge measured in coulombs and C is the capacitance, measured in farads.
The energy stored in a capacitor is found by integrating this equation. Starting with an uncharged capacitance (q = 0) and moving charge from one plate to the other until the plates have charge +Q and −Q requires the work W:
Nanoscale systems
The capacitance of nanoscale dielectric capacitors such as quantum dots may differ from conventional formulations of larger capacitors. In particular, the electrostatic potential difference experienced by electrons in conventional capacitors is spatially well-defined and fixed by the shape and size of metallic electrodes in addition to the statistically large number of electrons present in conventional capacitors. In nanoscale capacitors, however, the electrostatic potentials experienced by electrons are determined by the number and locations of all electrons that contribute to the electronic properties of the device. In such devices, the number of electrons may be very small, so the resulting spatial distribution of equipotential surfaces within the device is exceedingly complex.
Single-electron devices
The capacitance of a connected, or "closed", single-electron device is twice the capacitance of an unconnected, or "open", single-electron device. This fact may be traced more fundamentally to the energy stored in the single-electron device whose "direct polarization" interaction energy may be equally divided into the interaction of the electron with the polarized charge on the device itself due to the presence of the electron and the amount of potential energy required to form the polarized charge on the device (the interaction of charges in the device's dielectric material with the potential due to the electron).
Few-electron devices
The derivation of a "quantum capacitance" of a few-electron device involves the thermodynamic chemical potential of an N-particle system given by
whose energy terms may be obtained as solutions of the Schrödinger equation. The definition of capacitance, with the potential difference
may be applied to the device with the addition or removal of individual electrons, and
The "quantum capacitance" of the device is then
This expression of "quantum capacitance" may be written as which differs from the conventional expression described in the introduction where , the stored electrostatic potential energy, by a factor of 1/2 with .
However, within the framework of purely classical electrostatic interactions, the appearance of the factor of 1/2 is the result of integration in the conventional formulation involving the work done when charging a capacitor,
which is appropriate since for systems involving either many electrons or metallic electrodes, but in few-electron systems, . The integral generally becomes a summation. One may trivially combine the expressions of capacitance and electrostatic interaction energy, to obtain
which is similar to the quantum capacitance. A more rigorous derivation is reported in the literature. In particular, to circumvent the mathematical challenges of spatially complex equipotential surfaces within the device, an average electrostatic potential experienced by each electron is utilized in the derivation.
Apparent mathematical differences may be understood more fundamentally. The potential energy, , of an isolated device (self-capacitance) is twice that stored in a "connected" device in the lower limit . As grows large, . Thus, the general expression of capacitance is
In nanoscale devices such as quantum dots, the "capacitor" is often an isolated or partially isolated component within the device. The primary differences between nanoscale capacitors and macroscopic (conventional) capacitors are the number of excess electrons (charge carriers, or electrons, that contribute to the device's electronic behavior) and the shape and size of metallic electrodes. In nanoscale devices, nanowires consisting of metal atoms typically do not exhibit the same conductive properties as their macroscopic, or bulk material, counterparts.
Capacitance in electronic and semiconductor devices
In electronic and semiconductor devices, transient or frequency-dependent current between terminals contains both conduction and displacement components. Conduction current is related to moving charge carriers (electrons, holes, ions, etc.), while displacement current is caused by a time-varying electric field. Carrier transport is affected by electric fields and by a number of physical phenomena - such as carrier drift and diffusion, trapping, injection, contact-related effects, impact ionization, etc. As a result, device admittance is frequency-dependent, and a simple electrostatic formula for capacitance is not applicable. A more general definition of capacitance, encompassing electrostatic formula, is: where is the device admittance, and is the angular frequency.
In general, capacitance is a function of frequency. At high frequencies, capacitance approaches a constant value, equal to "geometric" capacitance, determined by the terminals' geometry and dielectric content in the device. A paper by Steven Laux presents a review of numerical techniques for capacitance calculation. In particular, capacitance can be calculated by a Fourier transform of a transient current in response to a step-like voltage excitation:
Negative capacitance in semiconductor devices
Usually, capacitance in semiconductor devices is positive. However, in some devices and under certain conditions (temperature, applied voltages, frequency, etc.), capacitance can become negative. Non-monotonic behavior of the transient current in response to a step-like excitation has been proposed as the mechanism of negative capacitance. Negative capacitance has been demonstrated and explored in many different types of semiconductor devices.
Measuring capacitance
Main article: Capacitance meterA capacitance meter is a piece of electronic test equipment used to measure capacitance, mainly of discrete capacitors. For most purposes and in most cases the capacitor must be disconnected from circuit.
Many DVMs (digital volt meters) have a capacitance-measuring function. These usually operate by charging and discharging the capacitor under test with a known current and measuring the rate of rise of the resulting voltage; the slower the rate of rise, the larger the capacitance. DVMs can usually measure capacitance from nanofarads to a few hundred microfarads, but wider ranges are not unusual. It is also possible to measure capacitance by passing a known high-frequency alternating current through the device under test and measuring the resulting voltage across it (does not work for polarised capacitors).

More sophisticated instruments use other techniques such as inserting the capacitor-under-test into a bridge circuit. By varying the values of the other legs in the bridge (so as to bring the bridge into balance), the value of the unknown capacitor is determined. This method of indirect use of measuring capacitance ensures greater precision. Through the use of Kelvin connections and other careful design techniques, these instruments can usually measure capacitors over a range from picofarads to farads.
See also
- Capacitive displacement sensor
- Capacity of a set
- Displacement current
- Gauss law
- LCR meter
- Magnetocapacitance
- Quantum capacitance
References
- Harrington, Roger F. (2003). Introduction to Electromagnetic Engineering (1st ed.). Dover Publications. p. 43. ISBN 0-486-43241-6.
- ^ "Lecture notes: Capacitance and Dieletrics" (PDF). University of New South Wales. Archived from the original (PDF) on 26 February 2009.
- "Definition of 'farad'". Collins.
- William D. Greason (1992). Electrostatic discharge in electronics. Research Studies Press. p. 48. ISBN 978-0-86380-136-5.
- Tipler, Paul; Mosca, Gene (2004). Physics for Scientists and Engineers (5th ed.). Macmillan. p. 752. ISBN 978-0-7167-0810-0.
- Massarini, A.; Kazimierczuk, M. K. (1997). "Self capacitance of inductors". IEEE Transactions on Power Electronics. 12 (4): 671–676. Bibcode:1997ITPE...12..671M. CiteSeerX 10.1.1.205.7356. doi:10.1109/63.602562: example of the use of the term 'self capacitance'.
{{cite journal}}: CS1 maint: postscript (link) - Jackson, John David (1999). Classical Electrodynamic (3rd ed.). John Wiley & Sons. p. 43. ISBN 978-0-471-30932-1.
- Maxwell, James (1873). "3". A treatise on electricity and magnetism. Vol. 1. Clarendon Press. p. 88ff.
- "Capacitance: Charge as a Function of Voltage". Av8n.com. Retrieved 20 September 2010.
- Smolić, Ivica; Klajn, Bruno (2021). "Capacitance matrix revisited". Progress in Electromagnetics Research B. 92: 1–18. arXiv:2007.10251. doi:10.2528/PIERB21011501. Retrieved 4 May 2021.
- "Capacitor MF-MMFD Conversion Chart". Just Radios.
- Fundamentals of Electronics. Vol. 1b – Basic Electricity – Alternating Current. Bureau of Naval Personnel. 1965. p. 197.
- Dawes, Chester L. (1973). "Capacitance and potential gradients of eccentric cylindrical condensers". Physics. 4 (2): 81–85. doi:10.1063/1.1745162.
- ^ Jackson, J. D. (1975). Classical Electrodynamics. Wiley. p. 80.
- Binns; Lawrenson (1973). Analysis and computation of electric and magnetic field problems. Pergamon Press. ISBN 978-0-08-016638-4.
- ^ Maxwell, J.;C. (1873). A Treatise on Electricity and Magnetism. Dover. p. 266 ff. ISBN 978-0-486-60637-8.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Rawlins, A.D. (1985). "Note on the capacitance of two closely separated spheres". IMA Journal of Applied Mathematics. 34 (1): 119–120. doi:10.1093/imamat/34.1.119.
- Gasper; Rahman (2004). Basic Hypergeometric Series. Cambridge University Press. p.20-22. ISBN 978-0-521-83357-8.
- Jackson, J.D. (1975). Classical Electrodynamics. Wiley. p. 128, problem 3.3.
- Maxwell, J. C. (1878). "On the electrical capacity of a long narrow cylinder and of a disk of sensible thickness". Proceedings of the London Mathematical Society. IX: 94–101. doi:10.1112/plms/s1-9.1.94.
- Vainshtein, L. A. (1962). "Static boundary problems for a hollow cylinder of finite length. III Approximate formulas". Zhurnal Tekhnicheskoi Fiziki. 32: 1165–1173.
- Jackson, J. D. (2000). "Charge density on thin straight wire, revisited". American Journal of Physics. 68 (9): 789–799. Bibcode:2000AmJPh..68..789J. doi:10.1119/1.1302908.
- Raphael Tsu (2011). Superlattice to Nanoelectronics. Elsevier. pp. 312–315. ISBN 978-0-08-096813-1.
- ^ T. LaFave Jr. (2011). "Discrete charge dielectric model of electrostatic energy". J. Electrostatics. 69 (6): 414–418. arXiv:1203.3798. doi:10.1016/j.elstat.2011.06.006. S2CID 94822190.
- G. J. Iafrate; K. Hess; J. B. Krieger; M. Macucci (1995). "Capacitive nature of atomic-sized structures". Phys. Rev. B. 52 (15): 10737–10739. Bibcode:1995PhRvB..5210737I. doi:10.1103/physrevb.52.10737. PMID 9980157.
- T. LaFave Jr; R. Tsu (March–April 2008). "Capacitance: A property of nanoscale materials based on spatial symmetry of discrete electrons" (PDF). Microelectronics Journal. 39 (3–4): 617–623. doi:10.1016/j.mejo.2007.07.105. Archived from the original (PDF) on 22 February 2014. Retrieved 12 February 2014.
- ^ Laux, S.E. (October 1985). "Techniques for small-signal analysis of semiconductor devices". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 4 (4): 472–481. doi:10.1109/TCAD.1985.1270145. S2CID 13058472.
- Jonscher, A.K. (1986). "The physical origin of negative capacitance". J. Chem. Soc. Faraday Trans. II. 82: 75–81. doi:10.1039/F29868200075.
- Ershov, M.; Liu, H.C.; Li, L.; Buchanan, M.; Wasilewski, Z.R.; Jonscher, A.K. (October 1998). "Negative capacitance effect in semiconductor devices". IEEE Trans. Electron Devices. 45 (10): 2196–2206. arXiv:cond-mat/9806145. Bibcode:1998ITED...45.2196E. doi:10.1109/16.725254. S2CID 204925581.
Further reading
- Tipler, Paul (1998). Physics for Scientists and Engineers: Vol. 2: Electricity and Magnetism, Light (4th ed.). W. H. Freeman. ISBN 1-57259-492-6
- Serway, Raymond; Jewett, John (2003). Physics for Scientists and Engineers (6th ed.). Brooks Cole. ISBN 0-534-40842-7
- Saslow, Wayne M.(2002). Electricity, Magnetism, and Light. Thomson Learning. ISBN 0-12-619455-6. See Chapter 8, and especially pp. 255–259 for coefficients of potential.
External links
 Media related to Capacitance at Wikimedia Commons
Media related to Capacitance at Wikimedia Commons


 where
where
 is the charge held,
is the charge held, is the electric potential,
is the electric potential, is the surface charge density,
is the surface charge density, is an infinitesimal element of area on the surface of the conductor, over which the surface charge density is integrated,
is an infinitesimal element of area on the surface of the conductor, over which the surface charge density is integrated, is the length from
is the length from  is the
is the  in free space (i.e. far away from any other charge distributions) is:
in free space (i.e. far away from any other charge distributions) is:

 and
and  , and
, and  gives the
gives the  is given by
is given by  where
where  is the instantaneous rate of change of voltage, and
is the instantaneous rate of change of voltage, and  is the instantaneous rate of change of the capacitance. For most applications, the change in capacitance over time is negligible, so the formula reduces to:
is the instantaneous rate of change of the capacitance. For most applications, the change in capacitance over time is negligible, so the formula reduces to:

 :
:

 does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case,
does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case,  , then the voltage at conductor 1 is given by
, then the voltage at conductor 1 is given by
 and similarly for the other voltages.
and similarly for the other voltages.  , etc. Thus the system can be described by a collection of coefficients known as the elastance matrix or reciprocal capacitance matrix, which is defined as:
, etc. Thus the system can be described by a collection of coefficients known as the elastance matrix or reciprocal capacitance matrix, which is defined as:

 between two objects can be defined by solving for the total charge
between two objects can be defined by solving for the total charge  and using
and using  .
.

 is known as the capacitance matrix, and is the
is known as the capacitance matrix, and is the  separated by a distance
separated by a distance  . If
. If 

 is the
is the  );
); is the
is the  for air); and
for air); and where
where  with a constant potential
with a constant potential  on the 2-dimensional surface of the conductors embedded in 3-space. This is simplified by symmetries. There is no solution in terms of elementary functions in more complicated cases.
on the 2-dimensional surface of the conductors embedded in 3-space. This is simplified by symmetries. There is no solution in terms of elementary functions in more complicated cases.

 :
: 

 : Outer radius
: Outer radius : Inner radius
: Inner radius : Wire length
: Wire length

 : Wire radius
: Wire radius

 : Strip width
: Strip width


 :
: 



 :
: 
 : the q-digamma function
: the q-digamma function : the
: the 
 : Radius
: Radius : Distance,
: Distance, 


 : Radius
: Radius

 : Length
: Length
 where W is the work measured in joules, q is the charge measured in coulombs and C is the capacitance, measured in farads.
where W is the work measured in joules, q is the charge measured in coulombs and C is the capacitance, measured in farads.


 with the potential difference
with the potential difference

 and
and 

 which differs from the conventional expression described in the introduction where
which differs from the conventional expression described in the introduction where  , the stored electrostatic potential energy,
, the stored electrostatic potential energy,
 by a factor of 1/2 with
by a factor of 1/2 with  .
.

 for systems involving either many electrons or metallic electrodes, but in few-electron systems,
for systems involving either many electrons or metallic electrodes, but in few-electron systems,  . The integral generally becomes a summation. One may trivially combine the expressions of capacitance
. The integral generally becomes a summation. One may trivially combine the expressions of capacitance
 and electrostatic interaction energy,
and electrostatic interaction energy,
 to obtain
to obtain

 , of an isolated device (self-capacitance) is twice that stored in a "connected" device in the lower limit
, of an isolated device (self-capacitance) is twice that stored in a "connected" device in the lower limit  . As
. As  grows large,
grows large,  . Thus, the general expression of capacitance is
. Thus, the general expression of capacitance is

 is not applicable. A more general definition of capacitance, encompassing electrostatic formula, is:
is not applicable. A more general definition of capacitance, encompassing electrostatic formula, is:
 where
where  is the device admittance, and
is the device admittance, and  is the angular frequency.
is the angular frequency.
