| Revision as of 21:17, 5 December 2019 editPokipsy76 (talk | contribs)Extended confirmed users2,250 edits →Example: expressing in matrix form to show it is area preserving← Previous edit | Latest revision as of 23:30, 14 October 2024 edit undoChaosand (talk | contribs)37 edits Clarified that the method had been "discovered" many times earlier. | ||
| (14 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
| In mathematics, the '''semi-implicit Euler method''', also called '''symplectic Euler''', '''semi-explicit Euler''', '''Euler–Cromer''', and '''Newton–Størmer–Verlet (NSV)''', is a modification of the ] for solving ], a system of ]s that arises in ]. It is a ] and hence it yields better results than the standard Euler method. | {{Short description|Modification of the Euler method for solving Hamilton's equations}} | ||
| In mathematics, the '''semi-implicit Euler method''', also called '''symplectic Euler''', '''semi-explicit Euler''', '''Euler–Cromer''', and '''Newton–Størmer–Verlet (NSV)''', is a modification of the ] for solving ], a system of ]s that arises in ]. It is a ] and hence it yields better results than the standard Euler method. | |||
| == |
== Origin == | ||
| The method was accidentally discovered by ] senior student Abby Aspel in 1980. In a lab assignment simulating orbits using Kepler's Law, which required computation in ]: she accidentally reversed two lines of code by calculating velocity before position. Her simulation converged more quickly and resulted in more accurate and feasible results than what was expected. Alan Cromer then proved why her algorithm was more stable than previous methods of computation.<ref>{{Cite journal |last=Cromer |first=Alan |date=1981-05-01 |title=Stable solutions using the Euler approximation |url=https://doi.org/10.1119/1.12478 |journal=American Journal of Physics |volume=49 |issue=5 |pages=455–459 |doi=10.1119/1.12478 |issn=0002-9505}}</ref> | |||
| The method, however, has been discovered and forgotten many times, dating back to Newton's ''Principiae'',<ref name="hairer2003" /> as recalled by Richard Feynman in his ''Feynman Lectures'' (Vol. 1, Sec. 9.6)<ref name="feynman1963" /> In modern times, the method was rediscovered in a 1956 preprint by René De Vogelaere that, although never formally published, influenced subsequent work on higher-order symplectic methods.<ref name="skeel2003" /> | |||
| ⚫ | The semi-implicit Euler method can be applied to a pair of ]s of the form | ||
| :<math> {dx \over dt} = f(t,v) </math>{{citation needed|date=September 2019}} | |||
| ⚫ | |||
| == Setting == | |||
| ⚫ | The semi-implicit Euler method can be applied to a pair of ]s of the form{{citation needed|date=September 2019}} | ||
| :<math>\begin{align} | |||
| {dx \over dt} &= f(t,v) \\ | |||
| ⚫ | {dv \over dt} &= g(t,x), | ||
| \end{align}</math> | |||
| where ''f'' and ''g'' are given functions. Here, ''x'' and ''v'' may be either scalars or vectors. The equations of motion in ] take this form if the Hamiltonian is of the form | where ''f'' and ''g'' are given functions. Here, ''x'' and ''v'' may be either scalars or vectors. The equations of motion in ] take this form if the Hamiltonian is of the form | ||
| Line 25: | Line 33: | ||
| \end{align}</math> | \end{align}</math> | ||
| where Δ''t'' is the time step and ''t<sub>n</sub>'' = ''t<sub>0</sub> |
where Δ''t'' is the time step and ''t<sub>n</sub>'' = ''t''<sub>0</sub> + ''n''Δ''t'' is the time after ''n'' steps. | ||
| The difference with the standard Euler method is that the semi-implicit Euler method uses ''v''<sub>''n''+1</sub> in the equation for ''x''<sub>''n''+1</sub>, while the Euler method uses ''v<sub>n</sub>''. | The difference with the standard Euler method is that the semi-implicit Euler method uses ''v''<sub>''n''+1</sub> in the equation for ''x''<sub>''n''+1</sub>, while the Euler method uses ''v<sub>n</sub>''. | ||
| Applying the method with negative time step to the computation of <math>(x_n,v_n)</math> from <math>(x_{n+1},v_{n+1})</math> and rearranging leads to the second variant of the semi-implicit Euler method | Applying the method with negative time step to the computation of <math>(x_n, v_n)</math> from <math>(x_{n+1}, v_{n+1})</math> and rearranging leads to the second variant of the semi-implicit Euler method | ||
| :<math>\begin{align} | :<math>\begin{align} | ||
| x_{n+1} &= x_n + f(t_n, v_n) \, \Delta t\\ | x_{n+1} &= x_n + f(t_n, v_n) \, \Delta t\\ | ||
| v_{n+1} &= v_n + g(t_n, x_{n+1}) \, \Delta t | v_{n+1} &= v_n + g(t_n, x_{n+1}) \, \Delta t | ||
| \end{align}</math> | \end{align}</math> | ||
| Line 40: | Line 48: | ||
| Alternating between the two variants of the semi-implicit Euler method leads in one simplification to the Störmer-] and in a slightly different simplification to the ], increasing both the order of the error and the order of preservation of energy.<ref name="hairer2003" /> | Alternating between the two variants of the semi-implicit Euler method leads in one simplification to the Störmer-] and in a slightly different simplification to the ], increasing both the order of the error and the order of preservation of energy.<ref name="hairer2003" /> | ||
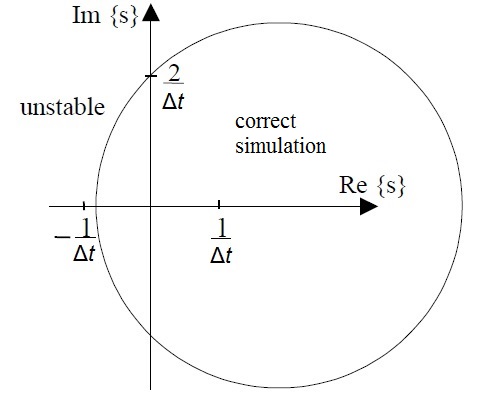
| The stability region of the semi-implicit method was presented by Niiranen<ref> Proceedings of the Electrimacs'99, Sept. 14-16, 1999 Lisboa, Portugal, Vol. 1, pages 71 - 78.</ref> although the semi-implicit Euler was misleadingly called symmetric Euler in his paper. The semi-implicit method models the simulated system correctly if the complex roots of the characteristic equation are within the circle shown below. For real roots the stability region extends outside the circle for which the |
The stability region of the semi-implicit method was presented by Niiranen<ref> Proceedings of the Electrimacs'99, Sept. 14-16, 1999 Lisboa, Portugal, Vol. 1, pages 71 - 78.</ref> although the semi-implicit Euler was misleadingly called symmetric Euler in his paper. The semi-implicit method models the simulated system correctly if the complex roots of the characteristic equation are within the circle shown below. For real roots the stability region extends outside the circle for which the criterion is <math>s > - 2/\Delta t</math> | ||
| ] | ] | ||
| Line 62: | Line 70: | ||
| \end{align}</math> | \end{align}</math> | ||
| Substituting <math>v_{n+1}</math> in the second equation with the expression given by the first equation, the iteration can be expressed in the following matrix form | |||
| :<math>\begin{bmatrix} x_{n+1} \\v_{n+1}\end{bmatrix} = | :<math>\begin{bmatrix} x_{n+1} \\v_{n+1}\end{bmatrix} = | ||
| \begin{bmatrix} | \begin{bmatrix} | ||
| Line 68: | Line 76: | ||
| -\omega^2 \Delta t & 1 | -\omega^2 \Delta t & 1 | ||
| \end{bmatrix} \begin{bmatrix} x_{n} \\ v_{n} \end{bmatrix},</math> | \end{bmatrix} \begin{bmatrix} x_{n} \\ v_{n} \end{bmatrix},</math> | ||
| and since the determinant of the matrix is 1 the transformation is area-preserving. | and since the ] of the matrix is 1 the transformation is area-preserving. | ||
| The iteration preserves the modified energy functional <math>E_h(x,v)=\tfrac12\left(v^2+\omega^2\,x^2-\omega^2\Delta t\,vx\right)</math> exactly, leading to stable periodic orbits (for sufficiently small step size) that deviate by <math>O(\Delta t)</math> from the exact orbits. The exact circular frequency <math>\omega</math> increases in the numerical approximation by a factor of <math>1+\tfrac1{24}\omega^2\Delta t^2+O(\Delta t^4)</math>. | The iteration preserves the modified energy functional <math>E_h(x,v)=\tfrac12\left(v^2+\omega^2\,x^2-\omega^2\Delta t\,vx\right)</math> exactly, leading to stable periodic orbits (for sufficiently small step size) that deviate by <math>O(\Delta t)</math> from the exact orbits. The exact circular frequency <math>\omega</math> increases in the numerical approximation by a factor of <math>1+\tfrac1{24}\omega^2\Delta t^2+O(\Delta t^4)</math>. | ||
| Line 75: | Line 83: | ||
| <references> | <references> | ||
| <ref name="hairer2003">{{cite journal | <ref name="hairer2003">{{cite journal | ||
| | |
| first1=Ernst | last1=Hairer | ||
| | first2=Christian | last2=Lubich | | first2=Christian | last2=Lubich | ||
| | first3=Gerhard | last3=Wanner | | first3=Gerhard | last3=Wanner | ||
| Line 83: | Line 91: | ||
| | volume = 12 | | volume = 12 | ||
| | pages = 399–450 | | pages = 399–450 | ||
| | url=http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.7.7106 | |||
| | doi=10.1017/S0962492902000144 | | doi=10.1017/S0962492902000144 | ||
| | bibcode=2003AcNum..12..399H | |||
| | citeseerx=10.1.1.7.7106 | |||
| | s2cid=122016794 | |||
| }}</ref> | }}</ref> | ||
| <ref name="skeel2003">{{cite arXiv | |||
| | last1 = Skeel | |||
| | first1 = Robert D. | |||
| | last2 = Cieśliński | |||
| | first2 = Jan L. | |||
| | date = | |||
| | title = On the famous unpublished preprint "Methods of integration which preserve the contact transformation property of the Hamilton equations" by René De Vogelaere | |||
| | eprint = 2003.12268 | |||
| }}</ref> | |||
| <ref name="feynman1963">{{cite book | |||
| ⚫ | | last = Feynman | ||
| ⚫ | | first = Richard P | ||
| | author-link = | |||
| | date = 1963 | |||
| | title = ''The Feynman Lectures on Physics'', Vol. 1, Sec. 9.6 | |||
| | url = https://www.feynmanlectures.caltech.edu/I_09.html | |||
| }}</ref> | |||
| </references> | </references> | ||
| * {{cite book |last= Giordano | |||
| * {{cite web|last=Nikolic|first=Branislav K.|title=Euler-Cromer method|publisher=] | url=http://www.physics.udel.edu/~bnikolic/teaching/phys660/numerical_ode/node2.html|accessdate=2021-09-29}} | |||
| |first= Nicholas J. | |||
| * {{cite book |last= Vesely|first= Franz J.|title= Computational Physics: An Introduction|url= https://archive.org/details/computationalphy00vese_143|url-access= limited|edition= 2nd|publisher= Springer|year= 2001|isbn= 978-0-306-46631-1|pages=}} | |||
| |author2=Hisao Nakanishi | |||
| * {{cite book |last= Giordano|first= Nicholas J.|author2=Hisao Nakanishi|title= Computational Physics|edition= 2nd|publisher= Benjamin Cummings|date=July 2005|isbn= 0-13-146990-8 }} | |||
| |title= Computational Physics | |||
| |edition= 2nd | |||
| |publisher= Benjamin Cummings | |||
| |date=July 2005 | |||
| |isbn= 0-13-146990-8 }} | |||
| * {{cite web | |||
| ⚫ | |||
| ⚫ | |||
| | title = The Euler-Cromer method | |||
| | publisher = ] | |||
| | url = http://www.physics.udel.edu/~jim/PHYS460_660_13S/Ordinary%20Differential%20Equations/Euler-Cromer%20Method.htm | |||
| | accessdate = 2013-04-11}} | |||
| * {{cite book |last= Vesely | |||
| |first= Franz J. | |||
| |title= Computational Physics: An Introduction | |||
| |edition= 2nd | |||
| |publisher= Springer | |||
| |year= 2001 | |||
| |isbn= 978-0-306-46631-1 | |||
| |pages=117}} | |||
| {{Numerical integrators}} | {{Numerical integrators}} | ||
Latest revision as of 23:30, 14 October 2024
Modification of the Euler method for solving Hamilton's equationsIn mathematics, the semi-implicit Euler method, also called symplectic Euler, semi-explicit Euler, Euler–Cromer, and Newton–Størmer–Verlet (NSV), is a modification of the Euler method for solving Hamilton's equations, a system of ordinary differential equations that arises in classical mechanics. It is a symplectic integrator and hence it yields better results than the standard Euler method.
Origin
The method was accidentally discovered by Newton North High School senior student Abby Aspel in 1980. In a lab assignment simulating orbits using Kepler's Law, which required computation in BASIC: she accidentally reversed two lines of code by calculating velocity before position. Her simulation converged more quickly and resulted in more accurate and feasible results than what was expected. Alan Cromer then proved why her algorithm was more stable than previous methods of computation.
The method, however, has been discovered and forgotten many times, dating back to Newton's Principiae, as recalled by Richard Feynman in his Feynman Lectures (Vol. 1, Sec. 9.6) In modern times, the method was rediscovered in a 1956 preprint by René De Vogelaere that, although never formally published, influenced subsequent work on higher-order symplectic methods.
Setting
The semi-implicit Euler method can be applied to a pair of differential equations of the form
where f and g are given functions. Here, x and v may be either scalars or vectors. The equations of motion in Hamiltonian mechanics take this form if the Hamiltonian is of the form
The differential equations are to be solved with the initial condition
The method
The semi-implicit Euler method produces an approximate discrete solution by iterating
where Δt is the time step and tn = t0 + nΔt is the time after n steps.
The difference with the standard Euler method is that the semi-implicit Euler method uses vn+1 in the equation for xn+1, while the Euler method uses vn.
Applying the method with negative time step to the computation of from and rearranging leads to the second variant of the semi-implicit Euler method
which has similar properties.
The semi-implicit Euler is a first-order integrator, just as the standard Euler method. This means that it commits a global error of the order of Δt. However, the semi-implicit Euler method is a symplectic integrator, unlike the standard method. As a consequence, the semi-implicit Euler method almost conserves the energy (when the Hamiltonian is time-independent). Often, the energy increases steadily when the standard Euler method is applied, making it far less accurate.
Alternating between the two variants of the semi-implicit Euler method leads in one simplification to the Störmer-Verlet integration and in a slightly different simplification to the leapfrog integration, increasing both the order of the error and the order of preservation of energy.
The stability region of the semi-implicit method was presented by Niiranen although the semi-implicit Euler was misleadingly called symmetric Euler in his paper. The semi-implicit method models the simulated system correctly if the complex roots of the characteristic equation are within the circle shown below. For real roots the stability region extends outside the circle for which the criterion is
As can be seen, the semi-implicit method can simulate correctly both stable systems that have their roots in the left half plane and unstable systems that have their roots in the right half plane. This is clear advantage over forward (standard) Euler and backward Euler. Forward Euler tends to have less damping than the real system when the negative real parts of the roots get near the imaginary axis and backward Euler may show the system be stable even when the roots are in the right half plane.
Example
The motion of a spring satisfying Hooke's law is given by
The semi-implicit Euler for this equation is
Substituting in the second equation with the expression given by the first equation, the iteration can be expressed in the following matrix form
and since the determinant of the matrix is 1 the transformation is area-preserving.
The iteration preserves the modified energy functional exactly, leading to stable periodic orbits (for sufficiently small step size) that deviate by from the exact orbits. The exact circular frequency increases in the numerical approximation by a factor of .
References
- Cromer, Alan (1981-05-01). "Stable solutions using the Euler approximation". American Journal of Physics. 49 (5): 455–459. doi:10.1119/1.12478. ISSN 0002-9505.
- ^ Hairer, Ernst; Lubich, Christian; Wanner, Gerhard (2003). "Geometric numerical integration illustrated by the Störmer/Verlet method". Acta Numerica. 12: 399–450. Bibcode:2003AcNum..12..399H. CiteSeerX 10.1.1.7.7106. doi:10.1017/S0962492902000144. S2CID 122016794.
- Feynman, Richard P (1963). The Feynman Lectures on Physics, Vol. 1, Sec. 9.6.
- Skeel, Robert D.; Cieśliński, Jan L. "On the famous unpublished preprint "Methods of integration which preserve the contact transformation property of the Hamilton equations" by René De Vogelaere". arXiv:2003.12268.
- Niiranen, Jouko: Fast and accurate symmetric Euler algorithm for electromechanical simulations Proceedings of the Electrimacs'99, Sept. 14-16, 1999 Lisboa, Portugal, Vol. 1, pages 71 - 78.
- Nikolic, Branislav K. "Euler-Cromer method". University of Delaware. Retrieved 2021-09-29.
- Vesely, Franz J. (2001). Computational Physics: An Introduction (2nd ed.). Springer. pp. 117. ISBN 978-0-306-46631-1.
- Giordano, Nicholas J.; Hisao Nakanishi (July 2005). Computational Physics (2nd ed.). Benjamin Cummings. ISBN 0-13-146990-8.
| Numerical methods for ordinary differential equations | |
|---|---|
| First-order methods | |
| Second-order methods | |
| Higher-order methods | |
| Theory | |




 from
from  and rearranging leads to the second variant of the semi-implicit Euler method
and rearranging leads to the second variant of the semi-implicit Euler method




 in the second equation with the expression given by the first equation, the iteration can be expressed in the following matrix form
in the second equation with the expression given by the first equation, the iteration can be expressed in the following matrix form

 exactly, leading to stable periodic orbits (for sufficiently small step size) that deviate by
exactly, leading to stable periodic orbits (for sufficiently small step size) that deviate by  from the exact orbits. The exact circular frequency
from the exact orbits. The exact circular frequency  increases in the numerical approximation by a factor of
increases in the numerical approximation by a factor of  .
.