| Revision as of 16:00, 1 November 2023 editJohnjbarton (talk | contribs)Extended confirmed users12,014 edits →Types of collisions: Remove duplicate content on types of collisions. May reintroduce section title← Previous edit | Revision as of 16:04, 1 November 2023 edit undoJohnjbarton (talk | contribs)Extended confirmed users12,014 edits move the dupe content from the intro into Types of collision in preparation for mergingNext edit → | ||
| Line 4: | Line 4: | ||
| ] | ] | ||
| In ], a '''collision''' is any event in which two or more bodies exert ]s on each other in a relatively short time. Although the most common use of the word ''collision'' refers to incidents in which two or more objects collide with great force, the scientific use of the term implies nothing about the magnitude of the force.<ref>{{Cite journal|last=Schmidt|first=Paul W.|date=2019|title=Collision (physics)|url=https://www.accessscience.com/content/collision-physics/149000|journal=Access Science|language=en|doi=10.1036/1097-8542.149000}}</ref> | In ], a '''collision''' is any event in which two or more bodies exert ]s on each other in a relatively short time. Although the most common use of the word ''collision'' refers to incidents in which two or more objects collide with great force, the scientific use of the term implies nothing about the magnitude of the force.<ref>{{Cite journal|last=Schmidt|first=Paul W.|date=2019|title=Collision (physics)|url=https://www.accessscience.com/content/collision-physics/149000|journal=Access Science|language=en|doi=10.1036/1097-8542.149000}}</ref> | ||
| == Types of collisions == | |||
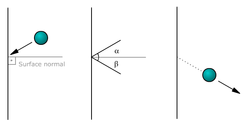
| ⚫ | ] happens when an object hits a plane surface. If the kinetic energy after impact is the same as before impact, it is an elastic collision. If kinetic energy is lost, it is an inelastic collision. The diagram does not show whether the illustrated collision was elastic or inelastic, because no velocities are provided. The most one can say is that the collision was not perfectly inelastic, because in that case the ball would have stuck to the wall.]] | ||
| ⚫ | Collision is short-duration interaction between two bodies or more than two bodies simultaneously causing change in motion of bodies involved due to internal forces acted between them during this. Collisions involve forces (there is a change in ]). The magnitude of the velocity difference just before impact is called the '''closing speed'''. All collisions conserve ]. What distinguishes different types of collisions is whether they also conserve ]. The line of impact is the line that is collinear to the common normal of the surfaces that are closest or in contact during impact. This is the line along which internal force of collision acts during impact, and Newton's ] is defined only along this line. Collisions are of three types: | ||
| ⚫ | #perfectly elastic collision | ||
| ⚫ | #inelastic collision | ||
| ⚫ | #perfectly inelastic collision. | ||
| In physics, collisions can be classified by the change in the total ] of the system before and after the collision: | In physics, collisions can be classified by the change in the total ] of the system before and after the collision: | ||
| Line 11: | Line 18: | ||
| * And if all of the total kinetic energy is conserved (i.e. no energy is released as sound, heat, etc.), the collision is said to be ''perfectly elastic''. Such a system is an ] and cannot occur in reality, due to the ]. | * And if all of the total kinetic energy is conserved (i.e. no energy is released as sound, heat, etc.), the collision is said to be ''perfectly elastic''. Such a system is an ] and cannot occur in reality, due to the ]. | ||
| == Physics == | |||
| ⚫ | ] happens when an object hits a plane surface. If the kinetic energy after impact is the same as before impact, it is an elastic collision. If kinetic energy is lost, it is an inelastic collision. The diagram does not show whether the illustrated collision was elastic or inelastic, because no velocities are provided. The most one can say is that the collision was not perfectly inelastic, because in that case the ball would have stuck to the wall.]] | ||
| ⚫ | Collision is short-duration interaction between two bodies or more than two bodies simultaneously causing change in motion of bodies involved due to internal forces acted between them during this. Collisions involve forces (there is a change in ]). The magnitude of the velocity difference just before impact is called the '''closing speed'''. All collisions conserve ]. What distinguishes different types of collisions is whether they also conserve ]. The line of impact is the line that is collinear to the common normal of the surfaces that are closest or in contact during impact. This is the line along which internal force of collision acts during impact, and Newton's ] is defined only along this line. Collisions are of three types: | ||
| ⚫ | #perfectly elastic collision | ||
| ⚫ | #inelastic collision | ||
| ⚫ | #perfectly inelastic collision. | ||
| Specifically, collisions can either be ''],'' meaning they conserve both momentum and kinetic energy, or ''],'' meaning they conserve momentum but not kinetic energy. | Specifically, collisions can either be ''],'' meaning they conserve both momentum and kinetic energy, or ''],'' meaning they conserve momentum but not kinetic energy. | ||
Revision as of 16:04, 1 November 2023
Instance of two or more bodies physically contacting each other within short period of time This article is about physics models. For accidents, see Collision (disambiguation).| This article may require cleanup to meet Misplaced Pages's quality standards. The specific problem is: organization. Please help improve this article if you can. (July 2022) (Learn how and when to remove this message) |

In physics, a collision is any event in which two or more bodies exert forces on each other in a relatively short time. Although the most common use of the word collision refers to incidents in which two or more objects collide with great force, the scientific use of the term implies nothing about the magnitude of the force.
Types of collisions
Collision is short-duration interaction between two bodies or more than two bodies simultaneously causing change in motion of bodies involved due to internal forces acted between them during this. Collisions involve forces (there is a change in velocity). The magnitude of the velocity difference just before impact is called the closing speed. All collisions conserve momentum. What distinguishes different types of collisions is whether they also conserve kinetic energy. The line of impact is the line that is collinear to the common normal of the surfaces that are closest or in contact during impact. This is the line along which internal force of collision acts during impact, and Newton's coefficient of restitution is defined only along this line. Collisions are of three types:
- perfectly elastic collision
- inelastic collision
- perfectly inelastic collision.
In physics, collisions can be classified by the change in the total kinetic energy of the system before and after the collision:
- If most or all of the total kinetic energy is lost (dissipated as heat, sound, etc. or absorbed by the objects themselves), the collision is said to be inelastic; such collisions involve objects coming to a full stop. An example of such a collision is a car crash, as cars crumple inward when crashing, rather than bouncing off of each other. This is by design, for the safety of the occupants and bystanders should a crash occur - the frame of the car absorbs the energy of the crash instead.
- If most of the kinetic energy is conserved (i.e. the objects continue moving afterwards), the collision is said to be elastic. An example of this is a baseball bat hitting a baseball - the kinetic energy of the bat is transferred to the ball, greatly increasing the ball's velocity. The sound of the bat hitting the ball represents the loss of energy.
- And if all of the total kinetic energy is conserved (i.e. no energy is released as sound, heat, etc.), the collision is said to be perfectly elastic. Such a system is an idealization and cannot occur in reality, due to the second law of thermodynamics.
Specifically, collisions can either be elastic, meaning they conserve both momentum and kinetic energy, or inelastic, meaning they conserve momentum but not kinetic energy.
An inelastic collision is sometimes also called a plastic collision. A "perfectly inelastic" collision (also called a "perfectly plastic" collision) is a limiting case of inelastic collision in which the two bodies coalesce after impact.
The degree to which a collision is elastic or inelastic is quantified by the coefficient of restitution, a value that generally ranges between zero and one. A perfectly elastic collision has a coefficient of restitution of one; a perfectly inelastic collision has a coefficient of restitution of zero.
Collisions in ideal gases approach perfectly elastic collisions, as do scattering interactions of sub-atomic particles which are deflected by the electromagnetic force. Some large-scale interactions like the slingshot type gravitational interactions between satellites and planets are almost perfectly elastic.
Analytical vs. numerical approaches towards resolving collisions
Relatively few problems involving collisions can be solved analytically; the remainder require numerical methods. An important problem in simulating collisions is determining whether two objects have in fact collided. This problem is called collision detection.
| This section may require cleanup to meet Misplaced Pages's quality standards. No cleanup reason has been specified. Please help improve this section if you can. (February 2011) (Learn how and when to remove this message) |
Examples of collisions that can be solved analytically
Billiards
Collisions play an important role in cue sports. Because the collisions between billiard balls are nearly elastic, and the balls roll on a surface that produces low rolling friction, their behavior is often used to illustrate Newton's laws of motion. After a zero-friction collision of a moving ball with a stationary one of equal mass, the angle between the directions of the two balls is 90 degrees. This is an important fact that professional billiards players take into account, although it assumes the ball is moving without any impact of friction across the table rather than rolling with friction. Consider an elastic collision in two dimensions of any two masses m1 and m2, with respective initial velocities u1 and u2 where u2 = 0, and final velocities V1 and V2. Conservation of momentum gives m1u1 = m1V1 + m2V2. Conservation of energy for an elastic collision gives (1/2)m1|u1| = (1/2)m1|V1| + (1/2)m2|V2|. Now consider the case m1 = m2: we obtain u1 = V1 + V2 and |u1| = |V1| + |V2|. Taking the dot product of each side of the former equation with itself, |u1| = u1•u1 = |V1| + |V2| + 2V1•V2. Comparing this with the latter equation gives V1•V2 = 0, so they are perpendicular unless V1 is the zero vector (which occurs if and only if the collision is head-on).
Perfect inelastic collision
In a perfect inelastic collision, i.e., a zero coefficient of restitution, the colliding particles coalesce. It is necessary to consider conservation of momentum:
where v is the final velocity, which is hence given by
The reduction of total kinetic energy is equal to the total kinetic energy before the collision in a center of momentum frame with respect to the system of two particles, because in such a frame the kinetic energy after the collision is zero. In this frame most of the kinetic energy before the collision is that of the particle with the smaller mass. In another frame, in addition to the reduction of kinetic energy there may be a transfer of kinetic energy from one particle to the other; the fact that this depends on the frame shows how relative this is. With time reversed we have the situation of two objects pushed away from each other, e.g. shooting a projectile, or a rocket applying thrust (compare the derivation of the Tsiolkovsky rocket equation).
Examples of collisions analyzed numerically
Animal locomotion
Collisions of an animal's foot or paw with the underlying substrate are generally termed ground reaction forces. These collisions are inelastic, as kinetic energy is not conserved. An important research topic in prosthetics is quantifying the forces generated during the foot-ground collisions associated with both disabled and non-disabled gait. This quantification typically requires subjects to walk across a force platform (sometimes called a "force plate") as well as detailed kinematic and dynamic (sometimes termed kinetic) analysis.
Collisions used as an experimental tool
Collisions can be used as an experimental technique to study material properties of objects and other physical phenomena.
Space exploration
An object may deliberately be made to crash-land on another celestial body, to do measurements and send them to Earth before being destroyed, or to allow instruments elsewhere to observe the effect. See e.g.:
- During Apollo 13, Apollo 14, Apollo 15, Apollo 16 and Apollo 17, the S-IVB (the rocket's third stage) was crashed into the Moon in order to perform seismic measurement used for characterizing the lunar core.
- Deep Impact
- SMART-1 - European Space Agency satellite
- Moon impact probe - ISRO probe and LCROSS with its spent Centaur Upper Stage - NASA Probe
- Double Asteroid Redirection Test for planetary defence
Mathematical description of molecular collisions
Let the linear, angular and internal momenta of a molecule be given by the set of r variables { pi }. The state of a molecule may then be described by the range δwi = δp1δp2δp3 ... δpr. There are many such ranges corresponding to different states; a specific state may be denoted by the index i. Two molecules undergoing a collision can thus be denoted by (i, j) (Such an ordered pair is sometimes known as a constellation.) It is convenient to suppose that two molecules exert a negligible effect on each other unless their center of gravity approach within a critical distance b. A collision therefore begins when the respective centers of gravity arrive at this critical distance, and is completed when they again reach this critical distance on their way apart. Under this model, a collision is completely described by the matrix , which refers to the constellation (i, j) before the collision, and the (in general different) constellation (k, l) after the collision. This notation is convenient in proving Boltzmann's H-theorem of statistical mechanics.
See also
- Ballistic pendulum
- Coefficient of restitution
- Collision detection
- Contact mechanics
- Elastic collision
- Friction
- Impact crater
- Impact event
- Inelastic collision
- Kinetic theory of gases - collisions between molecules
- Projectile
Notes
- Schmidt, Paul W. (2019). "Collision (physics)". Access Science. doi:10.1036/1097-8542.149000.
- Alciatore, David G. (January 2006). "TP 3.1 90° rule" (PDF). Archived (PDF) from the original on 2022-10-09. Retrieved 2008-03-08.
References
- Tolman, R. C. (1938). The Principles of Statistical Mechanics. Oxford: Clarendon Press. Reissued (1979) New York: Dover ISBN 0-486-63896-0.
External links
- Three Dimensional Collision - Oblique inelastic collision between two homogeneous spheres.
- One Dimensional Collision - One Dimensional Collision Flash Applet.
- Two Dimensional Collision - Two Dimensional Collision Flash Applet.



 , which refers to the constellation (i, j) before the collision, and the (in general different) constellation (k, l) after the collision.
This notation is convenient in proving Boltzmann's
, which refers to the constellation (i, j) before the collision, and the (in general different) constellation (k, l) after the collision.
This notation is convenient in proving Boltzmann's