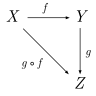| Revision as of 04:38, 26 August 2009 view sourceSławomir Biały (talk | contribs)Autopatrolled, Extended confirmed users, Pending changes reviewers12,807 edits revert: these "references" are of poor quality, are poorly formatted, and have nothing to do with the text they are attached to!← Previous edit | Revision as of 11:14, 28 August 2009 view source JAnDbot (talk | contribs)Bots159,117 editsm robot Adding: mdf:МатематиксьNext edit → | ||
| Line 278: | Line 278: | ||
| {{Link FA|mk}} | {{Link FA|mk}} | ||
| {{Link FA|vo}} | {{Link FA|vo}} | ||
| ] | ] | ||
| ] | ] | ||
| Line 373: | Line 374: | ||
| ] | ] | ||
| ] | ] | ||
| ] | |||
| ] | ] | ||
| ] | ] | ||
| Line 400: | Line 402: | ||
| ] | ] | ||
| ] | ] | ||
| ⚫ | ] | ||
| ] | ] | ||
| ] | ] | ||
| Line 426: | Line 429: | ||
| ] | ] | ||
| ] | ] | ||
| ⚫ | ] | ||
| ] | ] | ||
| ] | ] | ||
Revision as of 11:14, 28 August 2009
"Maths" and "Math" redirect here. For other uses of "Mathematics" or "Math", see Mathematics (disambiguation) and Math (disambiguation).

Mathematics is the science and study of quantity, structure, space, and change. Mathematicians seek out patterns, formulate new conjectures, and establish truth by rigorous deduction from appropriately chosen axioms and definitions.
There is debate over whether mathematical objects such as numbers and points exist naturally or are human creations. The mathematician Benjamin Peirce called mathematics "the science that draws necessary conclusions". Albert Einstein, on the other hand, stated that "as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality."
Through the use of abstraction and logical reasoning, mathematics evolved from counting, calculation, measurement, and the systematic study of the shapes and motions of physical objects. Practical mathematics has been a human activity for as far back as written records go (see: History of Mathematics). Rigorous arguments first appeared in Greek mathematics, most notably in Euclid's Elements. Mathematics continued to develop, in fitful bursts, until the Renaissance, when mathematical innovations interacted with new scientific discoveries, leading to an acceleration in research that continues to the present day.
Today, mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new disciplines. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind, although practical applications for what began as pure mathematics are often discovered later.
Etymology
The word "mathematics" comes from the Greek μάθημα (máthēma), which means learning, study, science, and additionally came to have the narrower and more technical meaning "mathematical study", even in Classical times. Its adjective is μαθηματικός (mathēmatikós), related to learning, or studious, which likewise further came to mean mathematical. In particular, Template:Polytonic (mathēmatikḗ tékhnē), in Latin ars mathematica, meant the mathematical art.
The apparent plural form in English, like the French plural form les mathématiques (and the less commonly used singular derivative la mathématique), goes back to the Latin neuter plural mathematica (Cicero), based on the Greek plural τα μαθηματικά (ta mathēmatiká), used by Aristotle, and meaning roughly "all things mathematical"; although it is plausible that English borrowed only the adjective mathematic(al) and formed the noun mathematics anew, after the pattern of physics and metaphysics, which were inherited from the Greek. In English, the noun mathematics takes singular verb forms. It is often shortened to maths, or math in English-speaking North America.
History
Main article: History of mathematics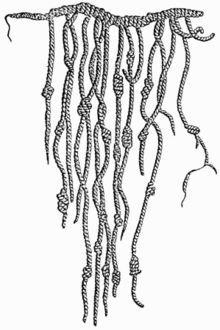
The evolution of mathematics might be seen as an ever-increasing series of abstractions, or alternatively an expansion of subject matter. The first abstraction, which is shared by many animals, was probably that of numbers: the realization that two apples and two oranges (for example) have something in common.
In addition to recognizing how to count physical objects, prehistoric peoples also recognized how to count abstract quantities, like time – days, seasons, years. Elementary arithmetic (addition, subtraction, multiplication and division) naturally followed.
Further steps needed writing or some other system for recording numbers such as tallies or the knotted strings called quipu used by the Inca to store numerical data. Numeral systems have been many and diverse, with the first known written numerals created by Egyptians in Middle Kingdom texts such as the Rhind Mathematical Papyrus. The Indus Valley civilization developed the modern decimal system, including the concept of zero.
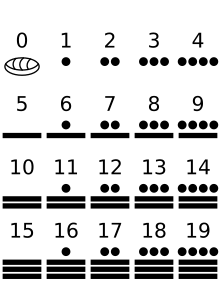
The earliest uses of mathematics were in trading, land measurement, painting and weaving patterns and the recording of time and nothing much more advanced until around 3000BC onwards when the Babylonians and Egyptians began using arithmetic, algebra and geometry for taxation and other financial calculations, building and construction and astronomy. The systematic study of mathematics in its own right began with the Ancient Greeks between 600 and 300BC.
Mathematics has since been greatly extended, and there has been a fruitful interaction between mathematics and science, to the benefit of both. Mathematical discoveries have been made throughout history and continue to be made today. According to Mikhail B. Sevryuk, in the January 2006 issue of the Bulletin of the American Mathematical Society, "The number of papers and books included in the Mathematical Reviews database since 1940 (the first year of operation of MR) is now more than 1.9 million, and more than 75 thousand items are added to the database each year. The overwhelming majority of works in this ocean contain new mathematical theorems and their proofs."
Inspiration, pure and applied mathematics, and aesthetics
Main article: Mathematical beauty
Mathematics arises from many different kinds of problems. At first these were found in commerce, land measurement and later astronomy; nowadays, all sciences suggest problems studied by mathematicians, and many problems arise within mathematics itself. For example, the physicist Richard Feynman invented the path integral formulation of quantum mechanics using a combination of mathematical reasoning and physical insight, and today's string theory, a still-developing scientific theory which attempts to unify the four fundamental forces of nature, continues to inspire new mathematics. Some mathematics is only relevant in the area that inspired it, and is applied to solve further problems in that area. But often mathematics inspired by one area proves useful in many areas, and joins the general stock of mathematical concepts. A distinction is often made between pure mathematics and applied mathematics however pure mathematics topics often turn out to have applications e.g. number theory in cryptography. This remarkable fact that even the "purest" mathematics often turns out to have practical applications is what Eugene Wigner has called "the unreasonable effectiveness of mathematics." As in most areas of study, the explosion of knowledge in the scientific age has led to specialization: there are now hundreds of specialized areas in mathematics and the latest Mathematics Subject Classification runs to 46 pages. Several areas of applied mathematics have merged with related traditions outside of mathematics and become disciplines in their own right, including statistics, operations research, and computer science.
For those who are mathematically inclined, there is often a definite aesthetic aspect to much of mathematics. Many mathematicians talk about the elegance of mathematics, its intrinsic aesthetics and inner beauty. Simplicity and generality are valued. There is beauty in a simple and elegant proof, such as Euclid's proof that there are infinitely many prime numbers, and in an elegant numerical method that speeds calculation, such as the fast Fourier transform. G. H. Hardy in A Mathematician's Apology expressed the belief that these aesthetic considerations are, in themselves, sufficient to justify the study of pure mathematics. Mathematicians often strive to find proofs of theorems that are particularly elegant, a quest Paul Erdős often referred to as finding proofs from "The Book" in which God had written down his favorite proofs. The popularity of recreational mathematics is another sign of the pleasure many find in solving mathematical questions.
Notation, language, and rigor

Most of the mathematical notation in use today was not invented until the 16th century. Before that, mathematics was written out in words, a painstaking process that limited mathematical discovery. In the 18th century, Euler was responsible for many of the notations in use today. Modern notation makes mathematics much easier for the professional, but beginners often find it daunting. It is extremely compressed: a few symbols contain a great deal of information. Like musical notation, modern mathematical notation has a strict syntax and encodes information that would be difficult to write in any other way.
Mathematical language can also be hard for beginners. Words such as or and only have more precise meanings than in everyday speech. Additionally, words such as open and field have been given specialized mathematical meanings. Mathematical jargon includes technical terms such as homeomorphism and integrable. But there is a reason for special notation and technical jargon: mathematics requires more precision than everyday speech. Mathematicians refer to this precision of language and logic as "rigor".
Mathematical proof is fundamentally a matter of rigor. Mathematicians want their theorems to follow from axioms by means of systematic reasoning. This is to avoid mistaken "theorems", based on fallible intuitions, of which many instances have occurred in the history of the subject. The level of rigor expected in mathematics has varied over time: the Greeks expected detailed arguments, but at the time of Isaac Newton the methods employed were less rigorous. Problems inherent in the definitions used by Newton would lead to a resurgence of careful analysis and formal proof in the 19th century. Today, mathematicians continue to argue among themselves about computer-assisted proofs. Since large computations are hard to verify, such proofs may not be sufficiently rigorous.
Axioms in traditional thought were "self-evident truths", but that conception is problematic. At a formal level, an axiom is just a string of symbols, which has an intrinsic meaning only in the context of all derivable formulas of an axiomatic system. It was the goal of Hilbert's program to put all of mathematics on a firm axiomatic basis, but according to Gödel's incompleteness theorem every (sufficiently powerful) axiomatic system has undecidable formulas; and so a final axiomatization of mathematics is impossible. Nonetheless mathematics is often imagined to be (as far as its formal content) nothing but set theory in some axiomatization, in the sense that every mathematical statement or proof could be cast into formulas within set theory.
Mathematics as science

Carl Friedrich Gauss referred to mathematics as "the Queen of the Sciences". In the original Latin Regina Scientiarum, as well as in German Königin der Wissenschaften, the word corresponding to science means (field of) knowledge. Indeed, this is also the original meaning in English, and there is no doubt that mathematics is in this sense a science. The specialization restricting the meaning to natural science is of later date. If one considers science to be strictly about the physical world, then mathematics, or at least pure mathematics, is not a science. Albert Einstein stated that "as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality."
Many philosophers believe that mathematics is not experimentally falsifiable, and thus not a science according to the definition of Karl Popper. However, in the 1930s important work in mathematical logic showed that mathematics cannot be reduced to logic, and Karl Popper concluded that "most mathematical theories are, like those of physics and biology, hypothetico-deductive: pure mathematics therefore turns out to be much closer to the natural sciences whose hypotheses are conjectures, than it seemed even recently." Other thinkers, notably Imre Lakatos, have applied a version of falsificationism to mathematics itself.
An alternative view is that certain scientific fields (such as theoretical physics) are mathematics with axioms that are intended to correspond to reality. In fact, the theoretical physicist, J. M. Ziman, proposed that science is public knowledge and thus includes mathematics. In any case, mathematics shares much in common with many fields in the physical sciences, notably the exploration of the logical consequences of assumptions. Intuition and experimentation also play a role in the formulation of conjectures in both mathematics and the (other) sciences. Experimental mathematics continues to grow in importance within mathematics, and computation and simulation are playing an increasing role in both the sciences and mathematics, weakening the objection that mathematics does not use the scientific method. In his 2002 book A New Kind of Science, Stephen Wolfram argues that computational mathematics deserves to be explored empirically as a scientific field in its own right.
The opinions of mathematicians on this matter are varied. Many mathematicians feel that to call their area a science is to downplay the importance of its aesthetic side, and its history in the traditional seven liberal arts; others feel that to ignore its connection to the sciences is to turn a blind eye to the fact that the interface between mathematics and its applications in science and engineering has driven much development in mathematics. One way this difference of viewpoint plays out is in the philosophical debate as to whether mathematics is created (as in art) or discovered (as in science). It is common to see universities divided into sections that include a division of Science and Mathematics, indicating that the fields are seen as being allied but that they do not coincide. In practice, mathematicians are typically grouped with scientists at the gross level but separated at finer levels. This is one of many issues considered in the philosophy of mathematics.
Mathematical awards are generally kept separate from their equivalents in science. The most prestigious award in mathematics is the Fields Medal, established in 1936 and now awarded every 4 years. It is often considered the equivalent of science's Nobel Prizes. The Wolf Prize in Mathematics, instituted in 1978, recognizes lifetime achievement, and another major international award, the Abel Prize, was introduced in 2003. These are awarded for a particular body of work, which may be innovation, or resolution of an outstanding problem in an established field. A famous list of 23 such open problems, called "Hilbert's problems", was compiled in 1900 by German mathematician David Hilbert. This list achieved great celebrity among mathematicians, and at least nine of the problems have now been solved. A new list of seven important problems, titled the "Millennium Prize Problems", was published in 2000. Solution of each of these problems carries a $1 million reward, and only one (the Riemann hypothesis) is duplicated in Hilbert's problems.
Fields of mathematics
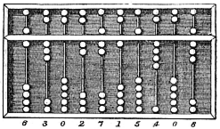
Mathematics can, broadly speaking, be subdivided into the study of quantity, structure, space, and change (i.e. arithmetic, algebra, geometry, and analysis). In addition to these main concerns, there are also subdivisions dedicated to exploring links from the heart of mathematics to other fields: to logic, to set theory (foundations), to the empirical mathematics of the various sciences (applied mathematics), and more recently to the rigorous study of uncertainty.
Quantity
The study of quantity starts with numbers, first the familiar natural numbers and integers ("whole numbers") and arithmetical operations on them, which are characterized in arithmetic. The deeper properties of integers are studied in number theory, from which come such popular results as Fermat's Last Theorem. Number theory also holds two widely-considered unsolved problems: the twin prime conjecture and Goldbach's conjecture.
As the number system is further developed, the integers are recognized as a subset of the rational numbers ("fractions"). These, in turn, are contained within the real numbers, which are used to represent continuous quantities. Real numbers are generalized to complex numbers. These are the first steps of a hierarchy of numbers that goes on to include quarternions and octonions. Consideration of the natural numbers also leads to the transfinite numbers, which formalize the concept of counting to infinity. Another area of study is size, which leads to the cardinal numbers and then to another conception of infinity: the aleph numbers, which allow meaningful comparison of the size of infinitely large sets.
Space
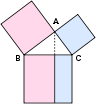
The study of space originates with geometry – in particular, Euclidean geometry. Trigonometry is the branch of mathematics that deals with relationships between the sides and the angles of triangles and with the trigonometric functions; it combines space and numbers, and encompasses the well-known Pythagorean theorem. The modern study of space generalizes these ideas to include higher-dimensional geometry, non-Euclidean geometries (which play a central role in general relativity) and topology. Quantity and space both play a role in analytic geometry, differential geometry, and algebraic geometry. Within differential geometry are the concepts of fiber bundles and calculus on manifolds, in particular, vector and tensor calculus. Within algebraic geometry is the description of geometric objects as solution sets of polynomial equations, combining the concepts of quantity and space, and also the study of topological groups, which combine structure and space. Lie groups are used to study space, structure, and change. Topology in all its many ramifications may have been the greatest growth area in 20th century mathematics, and includes the long-standing Poincaré conjecture and the controversial four color theorem, whose only proof, by computer, has never been verified by a human.
Change
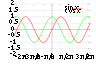
Understanding and describing change is a common theme in the natural sciences, and calculus was developed as a powerful tool to investigate it. Functions arise here, as a central concept describing a changing quantity. The rigorous study of real numbers and functions of a real variable is known as real analysis, with complex analysis the equivalent field for the complex numbers. Functional analysis focuses attention on (typically infinite-dimensional) spaces of functions. One of many applications of functional analysis is quantum mechanics. Many problems lead naturally to relationships between a quantity and its rate of change, and these are studied as differential equations. Many phenomena in nature can be described by dynamical systems; chaos theory makes precise the ways in which many of these systems exhibit unpredictable yet still deterministic behavior.
 |
 |
 |
 |

|
| Calculus | Vector calculus | Differential equations | Dynamical systems | Chaos theory |
Structure
Many mathematical objects, such as sets of numbers and functions, exhibit internal structure. The structural properties of these objects are investigated in the study of groups, rings, fields and other abstract systems, which are themselves such objects. This is the field of abstract algebra. An important concept here is that of vectors, generalized to vector spaces, and studied in linear algebra. The study of vectors combines three of the fundamental areas of mathematics: quantity, structure, and space. A number of ancient problems concerning Compass and straightedge constructions were finally solved using Galois theory.
Foundations and philosophy
In order to clarify the foundations of mathematics, the fields of mathematical logic and set theory were developed. Mathematical logic includes the mathematical study of logic and the applications of formal logic to other areas of mathematics; set theory is the branch of mathematics that studies sets or collections of objects. Category theory, which deals in an abstract way with mathematical structures and relationships between them, is still in development. The phrase "crisis of foundations" describes the search for a rigorous foundation for mathematics that took place from approximately 1900 to 1930. Some disagreement about the foundations of mathematics continues to present day. The crisis of foundations was stimulated by a number of controversies at the time, including the controversy over Cantor's set theory and the Brouwer-Hilbert controversy.
Mathematical logic is concerned with setting mathematics on a rigorous axiomatic framework, and studying the results of such a framework. As such, it is home to Gödel's second incompleteness theorem, perhaps the most widely celebrated result in logic, which (informally) implies that any formal system that contains basic arithmetic, if sound (meaning that all theorems that can be proven are true), is necessarily incomplete (meaning that there are true theorems which cannot be proved in that system). Gödel showed how to construct, whatever the given collection of number-theoretical axioms, a formal statement in the logic that is a true number-theoretical fact, but which does not follow from those axioms. Therefore no formal system is a true axiomatization of full number theory. Modern logic is divided into recursion theory, model theory, and proof theory, and is closely linked to theoretical computer science.
Discrete mathematics
Discrete mathematics is the common name for the fields of mathematics most generally useful in theoretical computer science. This includes computability theory, computational complexity theory, and information theory. Computability theory examines the limitations of various theoretical models of the computer, including the most powerful known model – the Turing machine. Complexity theory is the study of tractability by computer; some problems, although theoretically solvable by computer, are so expensive in terms of time or space that solving them is likely to remain practically unfeasible, even with rapid advance of computer hardware. Finally, information theory is concerned with the amount of data that can be stored on a given medium, and hence deals with concepts such as compression and entropy.
As a relatively new field, discrete mathematics has a number of fundamental open problems. The most famous of these is the "P=NP?" problem, one of the Millennium Prize Problems.
Applied mathematics
Applied mathematics considers the use of abstract mathematical tools in solving concrete problems in the sciences, business, and other areas.
Applied mathematics has significant overlap with the discipline of statistics, whose theory is formulated mathematically, especially with probability theory. Statisticians (working as part of a research project) "create data that makes sense" with random sampling and with randomized experiments; the design of a statistical sample or experiment specifies the analysis of the data (before the data be available). When reconsidering data from experiments and samples or when analyzing data from observational studies, statisticians "make sense of the data" using the art of modelling and the theory of inference – with model selection and estimation; the estimated models and consequential predictions should be tested on new data.
Computational mathematics proposes and studies methods for solving mathematical problems that are typically too large for human numerical capacity. Numerical analysis studies methods for problems in analysis using ideas of functional analysis and techniques of approximation theory; numerical analysis includes the study of approximation and discretization broadly with special concern for rounding errors. Other areas of computational mathematics include computer algebra and symbolic computation.
Common misconceptions
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (August 2009) (Learn how and when to remove this message) |
| This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (August 2009) (Learn how and when to remove this message) |
Mathematics is not a closed intellectual system, in which everything has already been worked out. There is no shortage of open problems. Every month, mathematicians publish many thousands of papers that embody new discoveries in the field.
Mathematics is not numerology; it is not concerned with "supernatural" properties of numbers. It is not accountancy; nor is it restricted to arithmetic.
Pseudomathematics is a form of mathematics-like activity undertaken outside academia, and occasionally by mathematicians themselves. It often consists of determined attacks on famous questions, consisting of proof-attempts made in an isolated way (that is, long papers not supported by previously published theory). The relationship to generally accepted mathematics is similar to that between pseudoscience and real science. The misconceptions involved are normally based on:
- misunderstanding of the implications of mathematical rigor;
- attempts to circumvent the usual criteria for publication of mathematical papers in a learned journal after peer review, often in the belief that the journal is biased against the author;
- lack of familiarity with, and therefore underestimation of, the existing literature.
Like astronomy, mathematics owes much to amateur contributors such as Fermat and Mersenne.
See also
Template:Misplaced Pages-Books
Main articles: Outline of mathematics and Lists of mathematics topics- Definitions of mathematics
- Dyscalculia
- Iatromathematicians
- Logics
- Mathematical anxiety
- Mathematical game
- Mathematical model
- Mathematical problem
- Mathematical structure
- Mathematics and art
- Mathematics competitions
- Mathematics education
- Mathematics portal
- Pattern
- Philosophy of mathematics
Notes
- No likeness or description of Euclid's physical appearance made during his lifetime survived antiquity. Therefore, Euclid's depiction in works of art depends on the artist's imagination (see Euclid).
- Steen, L.A. (April 29, 1988). The Science of Patterns. Science, 240: 611–616. and summarized at Association for Supervision and Curriculum Development.
- Devlin, Keith, Mathematics: The Science of Patterns: The Search for Order in Life, Mind and the Universe (Scientific American Paperback Library) 1996, ISBN 9780716750475
- Jourdain
- Peirce, p.97
- ^ Einstein, p. 28. The quote is Einstein's answer to the question: "how can it be that mathematics, being after all a product of human thought which is independent of experience, is so admirably appropriate to the objects of reality?" He, too, is concerned with The Unreasonable Effectiveness of Mathematics in the Natural Sciences.
- Eves
- Peterson
- Both senses can be found in Plato. Liddell and Scott, s.voceμαθηματικός
- The Oxford Dictionary of English Etymology, Oxford English Dictionary, sub "mathematics", "mathematic", "mathematics"
- Template:Cite article
- See, for example, Raymond L. Wilder, Evolution of Mathematical Concepts; an Elementary Study, passim
- Kline 1990, Chapter 1.
- Sevryuk
- Johnson, Gerald W.; Lapidus, Michel L. (2002). The Feynman Integral and Feynman's Operational Calculus. Oxford University Press.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Eugene Wigner, 1960, "The Unreasonable Effectiveness of Mathematics in the Natural Sciences," Communications on Pure and Applied Mathematics 13(1): 1–14.
- Mathematics Subject Classification 2010
- Hardy, G. H. (1940). A Mathematician's Apology. Cambridge University Press.
- Gold, Bonnie; Simons, Rogers A. (2008). Proof and Other Dilemmas: Mathematics and Philosophy. MAA.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Aigner, Martin; Ziegler, Gunter M. (2001). Proofs from the Book. Springer.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Earliest Uses of Various Mathematical Symbols (Contains many further references)
- Kline, pp. 140 (on Diophantus; pp.261, on Vieta.
- See false proof for simple examples of what can go wrong in a formal proof. The history of the Four Color Theorem contains examples of false proofs accidentally accepted by other mathematicians at the time.
- Ivars Peterson, The Mathematical Tourist, Freeman, 1988, ISBN 0-7167-1953-3. p. 4 "A few complain that the computer program can't be verified properly," (in reference to the Haken-Apple proof of the Four Color Theorem).
- Patrick Suppes, Axiomatic Set Theory, Dover, 1972, ISBN 0-486-61630-4. p. 1, "Among the many branches of modern mathematics set theory occupies a unique place: with a few rare exceptions the entities which are studied and analyzed in mathematics may be regarded as certain particular sets or classes of objects."
- Zeidler, Eberhard (2004). Oxford User's Guide to Mathematics. Oxford, UK: Oxford University Press. p. 1188. ISBN 0198507631.
- Waltershausen
- Shasha, Dennis Elliot; Lazere, Cathy A. (1998). Out of Their Minds: The Lives and Discoveries of 15 Great Computer Scientists. Springer. p. 228.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Popper 1995, p. 56
- Ziman
- "The Fields Medal is now indisputably the best known and most influential award in mathematics." Monastyrsky
- Riehm
- Luke Howard Hodgkin & Luke Hodgkin, A History of Mathematics, Oxford University Press, 2005.
- Clay Mathematics Institute P=NP
- Like other mathematical sciences such as physics and computer science, statistics is an autonomous discipline rather than a branch of applied mathematics. Like research physicists and computer scientists, research statisticians are mathematical scientists. Many statisticians have a degree in mathematics, and some statisticians are also mathematicians.
References
- Benson, Donald C., The Moment of Proof: Mathematical Epiphanies, Oxford University Press, USA; New Ed edition (December 14, 2000). ISBN 0-19-513919-4.
- Boyer, Carl B., A History of Mathematics, Wiley; 2 edition (March 6, 1991). ISBN 0-471-54397-7. — A concise history of mathematics from the Concept of Number to contemporary Mathematics.
- Courant, R. and H. Robbins, What Is Mathematics? : An Elementary Approach to Ideas and Methods, Oxford University Press, USA; 2 edition (July 18, 1996). ISBN 0-19-510519-2.
- Davis, Philip J. and Hersh, Reuben, The Mathematical Experience. Mariner Books; Reprint edition (January 14, 1999). ISBN 0-395-92968-7. — A gentle introduction to the world of mathematics.
- Einstein, Albert (1923). "Sidelights on Relativity (Geometry and Experience)". P. Dutton., Co.
{{cite journal}}: Cite journal requires|journal=(help) - Eves, Howard, An Introduction to the History of Mathematics, Sixth Edition, Saunders, 1990, ISBN 0-03-029558-0.
- Gullberg, Jan, Mathematics — From the Birth of Numbers. W. W. Norton & Company; 1st edition (October 1997). ISBN 0-393-04002-X. — An encyclopedic overview of mathematics presented in clear, simple language.
- Hazewinkel, Michiel (ed.), Encyclopaedia of Mathematics. Kluwer Academic Publishers 2000. — A translated and expanded version of a Soviet mathematics encyclopedia, in ten (expensive) volumes, the most complete and authoritative work available. Also in paperback and on CD-ROM, and online.
- Jourdain, Philip E. B., The Nature of Mathematics, in The World of Mathematics, James R. Newman, editor, Dover, 2003, ISBN 0-486-43268-8.
- Kline, Morris, Mathematical Thought from Ancient to Modern Times, Oxford University Press, USA; Paperback edition (March 1, 1990). ISBN 0-19-506135-7.
- Monastyrsky, Michael (2001). "Some Trends in Modern Mathematics and the Fields Medal" (PDF). Canadian Mathematical Society. Retrieved 2006-07-28.
{{cite journal}}: Cite journal requires|journal=(help) - Oxford English Dictionary, second edition, ed. John Simpson and Edmund Weiner, Clarendon Press, 1989, ISBN 0-19-861186-2.
- The Oxford Dictionary of English Etymology, 1983 reprint. ISBN 0-19-861112-9.
- Pappas, Theoni, The Joy Of Mathematics, Wide World Publishing; Revised edition (June 1989). ISBN 0-933174-65-9.
- Peirce, Benjamin. "Linear Associative Algebra". American Journal of Mathematics (Vol. 4, No. 1/4. (1881).
{{cite journal}}:|issue=has extra text (help); Unknown parameter|, pages=ignored (help) JSTOR. - Peterson, Ivars, Mathematical Tourist, New and Updated Snapshots of Modern Mathematics, Owl Books, 2001, ISBN 0-8050-7159-8.
- Paulos, John Allen (1996). A Mathematician Reads the Newspaper. Anchor. ISBN 0-385-48254-X.
- Popper, Karl R. (1995). "On knowledge". In Search of a Better World: Lectures and Essays from Thirty Years. Routledge. ISBN 0-415-13548-6.
- Riehm, Carl (2002). "The Early History of the Fields Medal" (PDF). Notices of the AMS. 49 (7). AMS: 778–782.
{{cite journal}}: Unknown parameter|month=ignored (help) - Sevryuk, Mikhail B. (2006). "Book Reviews" (PDF). Bulletin of the American Mathematical Society. 43 (1): 101–109. doi:10.1090/S0273-0979-05-01069-4. Retrieved 2006-06-24.
{{cite journal}}: Unknown parameter|month=ignored (help) - Waltershausen, Wolfgang Sartorius von (1856, repr. 1965). Gauss zum Gedächtniss. Sändig Reprint Verlag H. R. Wohlwend. ASIN B0000BN5SQ ASIN: B0000BN5SQ. ISBN 3-253-01702-8.
{{cite book}}: Check|asin=value (help); Check date values in:|year=(help)CS1 maint: year (link) - Ziman, J.M., F.R.S. (1968). "Public Knowledge:An essay concerning the social dimension of science".
{{cite journal}}: Cite journal requires|journal=(help)CS1 maint: multiple names: authors list (link)
External links
- Free Mathematics books Free Mathematics books collection.
- Applications of High School Algebra
- Encyclopaedia of Mathematics online encyclopadia from Springer, Graduate-level reference work with over 8,000 entries, illuminating nearly 50,000 notions in mathematics.
- HyperMath site at Georgia State University
- FreeScience Library The mathematics section of FreeScience library
- Rusin, Dave: The Mathematical Atlas. A guided tour through the various branches of modern mathematics. (Can also be found here.)
- Polyanin, Andrei: EqWorld: The World of Mathematical Equations. An online resource focusing on algebraic, ordinary differential, partial differential (mathematical physics), integral, and other mathematical equations.
- Cain, George: Online Mathematics Textbooks available free online.
- Math & Logic: The history of formal mathematical, logical, linguistic and methodological ideas. In The Dictionary of the History of Ideas.
- Mathematician Biographies. The MacTutor History of Mathematics archive Extensive history and quotes from all famous mathematicians.
- Metamath. A site and a language, that formalize mathematics from its foundations.
- Nrich, a prize-winning site for students from age five from Cambridge University
- Open Problem Garden, a wiki of open problems in mathematics
- Planet Math. An online mathematics encyclopedia under construction, focusing on modern mathematics. Uses the GFDL, allowing article exchange with Misplaced Pages. Uses TeX markup.
- Some mathematics applets, at MIT
- Weisstein, Eric et al.: MathWorld: World of Mathematics. An online encyclopedia of mathematics.
- Patrick Jones' Video Tutorials on Mathematics
| Major mathematics areas | |
|---|---|
| Foundations | |
| Algebra | |
| Analysis | |
| Discrete | |
| Geometry | |
| Number theory | |
| Topology | |
| Applied | |
| Computational | |
| Related topics | |
Template:Link FA Template:Link FA Template:Link FA Template:Link FA Template:Link FA
Categories: