| Revision as of 01:21, 19 February 2006 edit67.170.150.163 (talk) →Lack of an absolute reference frame: changed "lead" to "led" -- Alan Hartley← Previous edit | Revision as of 03:47, 22 February 2006 edit undo131.215.6.88 (talk) →External linksNext edit → | ||
| Line 388: | Line 388: | ||
| * a humoristic animation about the special relativity for the general public, Yannick Mahé, 2005 | * a humoristic animation about the special relativity for the general public, Yannick Mahé, 2005 | ||
| * a computer program to show the effects of travelling close to the speed of light. | * a computer program to show the effects of travelling close to the speed of light. | ||
| * A beginner introduction to concepts of Special and General Relativity, as well as black holes and gravitational waves. | |||
| ==References== | ==References== | ||
Revision as of 03:47, 22 February 2006
- A simple introduction to this subject is provided in Special relativity for beginners
Special relativity (SR) or the special theory of relativity is the physical theory published in 1905 by Albert Einstein in his article "On the Electrodynamics of Moving Bodies". It replaced Newtonian notions of space and time and incorporated electromagnetism as represented by Maxwell's equations. The theory is called "special" because it applies the principle of relativity only to the "restricted" or "special" case of inertial reference frames in flat spacetime, where the effects of gravity can be ignored.
Special relativity inter-relates space and time in such a way that the speed of light is constant, and the theory leads to situations where two observers can disagree over time intervals and distances between events, but without ever disagreeing about what events actually happened. It shows that time can pass more slowly if an observer is moving, depending on their relative speed.
The theory also predicts the famous equation E=mc².
For History and motivation, see the article: History of special relativity
Postulates
Main article: Postulates of special relativity
1. First postulate (principle of relativity)
- The laws of electrodynamics and optics will be valid for all frames of reference in which the laws of mechanics hold good (non-accelerating frames).
In other words: Every physical theory should look the same mathematically to every inertial observer; the laws of physics are independent of the state of inertial motion.
2. Second postulate (invariance of c)
- Light is always propagated in empty space with a definite velocity c that is independent of the state of motion of the emitting body; here the velocity of light c is defined as the two-way velocity, determined with a single clock.
In other words: The speed of light in vacuum, commonly denoted c, is the same to all inertial observers, and does not depend on the velocity of the object emitting the light. An observer attempting to measure the speed of light's propagation will get the same answer no matter how the system's components are moving.
Lack of an absolute reference frame
The principle of relativity, which states that there is no stationary reference frame, dates back to Galileo, and was incorporated into Newtonian Physics. However, in the late 19 Century, Maxwell's equations led some physicists to suggest that the universe was filled with a substance known as "aether" (sometimes written "ether") to transmit Electromagnetic waves. Aether was thought to constitute an absolute reference frame against which speeds could be measured. In other words, the aether was the only fixed or motionless thing in the universe. Aether had some wonderful properties: it was sufficiently elastic that it could support electromagnetic waves, those waves could interact with matter, yet it offered no resistance to bodies passing through it. It was also postulated that light arose from vibrations of the aether. The results of various experiments, including the Michelson-Morley experiment, indicated that the Earth was always 'stationary' relative to the Aether — something that was difficult to explain, since the Earth is in orbit around the Sun. For many, the most elegant solution was to discard the notion of Aether and an absolute frame, and to adopt Einstein's postulates. Special Relativity is formulated so as to not assume that any particular frame of reference is special; rather, in relativity, a system appears to observe the same laws of physics independent of an observer's velocity with respect to it. In particular, the speed of light is always measured to be c, even when measured by multiple observers that are moving at different (but constant) velocities.
Consequences
Main article: Consequences of Special Relativity
Einstein has said that all of the consequences of Special Relativity can be found from examination of the Lorentz transformations.
These transformations, and hence Special Relativity, lead to different physical predictions than Newtonian mechanics when relative velocities become comparable to the speed of light. The speed of light is so much larger than anything humans encounter that some of the effects predicted by relativity are initially counter-intuitive:
- Time dilation - the time lapse between two events is not invariant from one observer to another, but is dependent on the relative speeds of the observers' reference frames. (e.g., the twin paradox which concerns a twin who flies off in a spaceship travelling near the speed of light and returns to discover that his twin has aged much more rapidly.)
- Lack of simultaneity - two events that occur simultaneously to one observer may occur at different times to another observer (lack of absolute simultaneity).
- Lorentz contraction - the dimensions (e.g., length) of an object as measured by one observer may be smaller from the results of measurements of the same object made by another observer. (e.g., the ladder paradox involves a long ladder travelling near the speed of light and being contained within a smaller garage.)
- Addition of velocities - speeds do not simply add, for example if a rocket is moving at 2/3 the speed of light relative to an observer, and the rocket fires a missile at 2/3 of the speed of light relative to the rocket, the missile does not exceed the speed of light.
- Mass and momentum - when gaining momentum the apparent mass of an object increases as well as the energy (giving the famous E=mc equation.)
The Lorentz transformations of space and time
- Full article: Lorentz transformations

In this animation, the vertical direction indicates time and the horizontal direction indicates distance, the dashed line is the spacetime trajectory ("world line") of the observer. The lower quarter of the diagram shows the events that are visible to the user, and the upper quarter shows the light cone- those that will be able to see the observer. The small dots are arbitrary events in spacetime.
The slope of the world line (deviation from being vertical) gives the relative velocity to the observer. Note how the view of spacetime changes when the observer accelerates.
Relativity theory depends on "reference frames". A reference frame is a point in space at rest, or in uniform motion, from which a position can be measured along 3 spatial axes. In addition, a reference frame has a clock, moving with the reference frame allowing the measurement of the time of events.
An event is an occurrence that can be assigned a single unique time and location in space relative to a reference frame: It is a "point" in space-time. Since the speed of light is constant in Relativity in each and every reference frame, pulses of light can be used to unambiguously measure distances and refer back the times that events occurred to the clock, even though light takes time to reach the clock after the event has transpired.
For example, the explosion of a firecracker may be considered to be an "event". We can completely specify an event by its four space-time coordinates: The time of occurrence and its 3-dimensional spatial location from a reference point. Let's call this reference frame .
In relativity theory we often want to calculate the position of a point from a different reference point.
Suppose we have a second reference frame , whose spatial axes and clock exactly coincide with that of at time zero, but it is moving at a constant velocity with respect to along the axis.
As we shall see, since there is no absolute reference frame in Relativity, a concept of 'moving' doesn't strictly exist, everything is always moving with respect to some other reference frame. Instead, in relativity theory any two frames that move at the same speed in the same direction are said to be comoving. Therefore and are not comoving.
Let's define the event to have space-time coordinates in system and in . Then the Lorentz transformation specifies that these coordinates are related in the following way:
where is called the Lorentz factor and is the speed of light in a vacuum.
As we can see the and coordinates are unaffected, but the and axes are mixed up by the transformation. In fact they are a form of rotation.
A quantity invariant under Lorentz transformations is known as a Lorentz scalar.
Lorentz Contraction and Time Dilation
Multiplying through we get:
Examination of the first term of the equation for in the Lorentz transformation shows that all positions in one frame are multiplied by gamma, a number greater than one, to calculate the spatial interval in the second non comoving frame. This may be correctly interpreted as a physical contraction of any object from full sized, and at rest in one frame, to the second frame in which it is moving. This is termed Lorentz Contraction.
Similarly, in the equation for time , is multiplied by gamma in the second non comoving frame. This may be interpreted as time proceeding more slowly when an object is moving relative to another frame of reference. This is termed Time Dilation.
It might be expected that since one frame seems contracted, from the contracted frame of reference, the other would seem expanded; and similar effects with time. However since the Lorentz equations are symmetrical with respect to opposite relative speed, each frame seemingly paradoxically sees the other as equally contracted and equally time dilated.
These effects are not merely appearances; the time in the different frame of references essentially do travel at different rates to each other and the lengths of objects really are physically changed whilst in relative motion.
See also the twin paradox.
Simultaneity
Special relativity holds that events that are simultaneous in one frame of reference need not be simultaneous in another frame of reference.
Simultaneity can be seen by considering the second term of the expanded Lorentz equation for . Here as the velocity varies two events move forwards or backwards in time relative to each other if they are physically separated in space. This can be observed in Diagram 1; some events may be observed moving from the past to the future and back again as acceleration between reference frames occurs and time passes.
Lack of simultaneity implies that, for example, the two ends of a moving rod actually are not equally old — so for example, a cast radioactive rod would be older and have lower activity at the trailing edge than the leading edge. Indeed, lack of simultaneity explains why Lorentz contraction occurs — the rod is partially tilted along the time axis as it accelerates, giving a foreshortening in the spatial dimension.
According to a paper by Los Alamos scientist James Terrell, the observability of the Lorentz contraction from the single point in space is impossible by optical instruments. For example a distant spherical galaxy moving across the Milky Way with velocity 0.99c would appear as spherical object in our optical instruments. Lorentz contraction of distant galaxies cannot be observed from Earth. . Lorentz contraction is nevertheless a real physical effect. Its measurement by widely spaced instruments used simultaneously in the given frame is possible.
Causality

In diagram 2 the interval AB is 'time-like'; i.e., there is a frame of reference in which event A and event B occur at the same location in space, separated only by occurring at different times. If A precedes B in that frame, then A precedes B in all frames. It is hypothetically possible for matter (or information) to travel from A to B, so there can be a causal relationship (with A the cause and B the effect).
The interval AC in the diagram is 'space-like'; i.e., there is a frame of reference in which event A and event C occur simultaneously, separated only in space. However there are also frames in which A precedes C (as shown) and frames in which C precedes A. Barring some way of traveling faster than light, it is not possible for any matter (or information) to travel from A to C or from C to A. Thus there is no direct causal connection between A and C. However, many points in spacetime would be in the light cone of both C and A and can be causally related to either or both of these events, and similarly both C and A could have been caused by an earlier event.
Since the set of points of spacetime that is in any events light cone is completely independent of reference frame, then causality is absolutely assured.
Addition of velocities
If the observer in sees an object moving along the axis at velocity , then the observer in the system will see the object moving with velocity where
- .
This equation can be derived from the space and time transformations above. Notice that if the object is moving at the speed of light in the system (i.e. ), then it will also be moving at the speed of light in the system. Also, if both and are small with respect to the speed of light, we will recover the intuitive Galilean transformation of velocities: .
Mass, momentum, and energy
In addition to modifying notions of space and time, special relativity forces one to reconsider the concepts of mass, momentum, and energy, all of which are important constructs in Newtonian mechanics. Special relativity shows, in fact, that these concepts are all different aspects of the same physical quantity in much the same way that it shows space and time to be interrelated.
There are a couple of (equivalent) ways to define momentum and energy in SR. One method uses conservation laws. If these laws are to remain valid in SR they must be true in every possible reference frame. However, if one does some simple thought experiments using the Newtonian definitions of momentum and energy one sees that these quantities are not conserved in SR. One can rescue the idea of conservation by making some small modifications to the definitions to account for relativistic velocities. It is these new definitions which are taken as the correct ones for momentum and energy in SR.
Given an object of invariant mass m0 traveling at velocity u the energy and momentum are given by
where γ (the Lorentz factor) is given by
and c is the speed of light. The term γ occurs frequently in relativity, and comes from the Lorentz transformation equations. The energy and momentum can be related through the formula
which is referred to as the relativistic energy-momentum equation. These equations can be more succinctly stated using the four-momentum and the four-velocity as
which can be viewed as a relativistic analogue of Newton's second law.
For velocities much smaller than those of light γ can be approximated using a Taylor series expansion and one finds that
Barring the first term in the energy expression (discussed below), these formulas agree exactly with the standard definitions of Newtonian kinetic energy and momentum. This is as it should be, for special relativity must agree with Newtonian mechanics at low velocities.
Looking at the above formulas for energy, one sees that when an object is at rest (u = 0 and γ = 1) there is a non-zero energy remaining:
This energy is referred to as rest energy. The rest energy does not cause any conflict with the Newtonian theory because it is a constant and, as far as kinetic energy is concerned, it is only differences in energy which are meaningful.
Taking this formula at face value, we see that in relativity, mass is simply another form of energy. In 1927 Einstein remarked about special relativity:
Under this theory mass is not an unalterable magnitude, but a magnitude dependent on (and, indeed, identical with) the amount of energy.
This formula becomes important when one measures the masses of different atomic nuclei. By looking at the difference in masses, one can predict which nuclei have extra stored energy which can be released by nuclear reactions, providing important information which was useful in the development of the nuclear bomb. The implications of this formula on 20th century life have made it one of the most famous equations in all of science.
Relativistic mass
Introductory physics courses and some older textbooks on special relativity sometimes define a relativistic mass which increases as the velocity of a body increases. According to the geometric interpretation of special relativity, this is often deprecated and the term 'mass' is reserved to mean 'rest mass' and is thus independent of the inertial frame, i.e., invariant.
Using the relativistic mass definition, the mass of an object may vary depending on the observer's inertial frame in the same way that other properties such as its length may do so. Defining such a quantity may sometimes be useful in that doing so simplifies a calculation by restricting it to a specific frame. For example, consider a body with an invariant mass m0 moving at some velocity relative to an observer's reference system. That observer defines the relativistic mass of that body as:
"Relativistic mass" should not be confused with the "longitudinal" and "transverse mass" definitions that were used around 1900 and that were based on an inconsistent application of the laws of Newton: those used F=ma for a variable mass, while relativistic mass corresponds to Newton's dynamic mass in which p=mv and F=dp/dt.
Note also that the body does not actually become more massive in its proper frame, since the relativistic mass is only different for an observer in a different frame. The only mass that is frame independent is the invariant mass. When using the relativistic mass, the used reference frame should be specified if it isn't already obvious or implied. It also goes almost without saying that the increase in relativistic mass does not come from an increased number of atoms in the object. Instead, each atom, indeed each subatomic particle increases its relativistic mass as the object accelerates.
Physics textbooks sometimes use the relativistic mass as it allows the students to utilize their knowledge of Newtonian physics to gain some intuitive grasp of relativity in their frame of choice (usually their own!). "Relativistic mass" is also consistent with the concepts "time dilation" and "length contraction".
The geometry of space-time
SR uses a 'flat' 4-dimensional Minkowski space, which is an example of a space-time. This space, however, is very similar to the standard 3 dimensional Euclidean space, and fortunately by that fact, very easy to work with.
The differential of distance(ds) in cartesian 3D space is defined as:
where are the differentials of the three spatial dimensions. In the geometry of special relativity, a fourth dimension, time, is added, with units of c, so that the equation for the differential of distance becomes:
In many situations it may be convenient to treat time as imaginary (e.g. it may simplify equations), in which case in the above equation is replaced by , and the metric becomes
This is, however, just a simplifying mathematical technique, and has no theoretical significance. The deeper development of the theory relies on the concept of the Minkowski metric as described below.
If we reduce the spatial dimensions to 2, so that we can represent the physics in a 3-D space
We see that the null geodesics lie along a dual-cone:
defined by the equation
or
Which is the equation of a circle with r=c*dt. If we extend this to three spatial dimensions, the null geodesics are continuous concentric spheres, with radius = distance = c×(±time).
This null dual-cone represents the "line of sight" of a point in space. That is, when we look at the stars and say "The light from that star which I am receiving is X years old.", we are looking down this line of sight: a null geodesic. We are looking at an event meters away and d/c seconds in the past. For this reason the null dual cone is also known as the 'light cone'. (The point in the lower left of the picture below represents the star, the origin represents the observer, and the line represents the null geodesic "line of sight".)
The cone in the −t region is the information that the point is 'receiving', while the cone in the +t section is the information that the point is 'sending'.
The geometry of Minkowski space can be depicted using Minkowski diagrams, which are also useful in understanding many of the thought-experiments in special relativity.
Physics in spacetime
Having recognised the four-dimensional nature of spacetime, we are driven to employ the Minkowski metric, η, given in components (valid in any reference frame) as
Then we recognise that co-ordinate transformations between inertial reference frames are given by the Lorentz transformation tensor Λ. For the special case of motion along the x-axis, we have:
where β and γ are defined as
This simplifies almost every formula ever encountered in special relativity. We understand that all proper physical quantities are given by tensors. So to transform from one frame to another, we use the well known tensor transformation law
To see how this is useful, we first recognise that position is a four vector, since in component form
So to transform it from an unprimed co-ordinate system S to a primed system S', we calculate
which is a nice way of arriving at the cumbersome looking definition of the Lorentz transformation given above. But the true power becomes evident when you recognise that all tensors transform by the same rule. Firstly, note that the scalar (in fact the length of the position four-vector) constructed as follows:
is invariant - i.e. it takes the same value in all inertial frames, simply because it is a 0 rank tensor, and so no copies of the Lorentz appears in its transformation: |x'| = |x|.
Recognising other physical quantities as tensors also simplifies their transformation laws. First note that the velocity four-vector U is given by
Recognising this, we can turn the awkward looking law about addition of velocities into a simple statement about transforming the velocity four-vector of one particle from one frame to another. The energy-momentum four-vector is given by (and in component form)
This gives us the invariant
We can work out what this invariant is by first arguing that, since it is a scalar, it doesn't matter which reference frame we calculate it, and then by transforming to a frame where the total momentum is zero. We then get the celebrated result
Further examples of physical tensors are the electromagnetic field tensor, and the stress-energy tensor, and again their transformation is given by the simple tensor transformation law.
The electric field and the magnetic field are now unified into the electromagnetic field tensor:
The charge density and current density are unified into the current-charge 4-vector:
and Maxwell's equations are reduced to two in number. (see Maxwell's Equations#Formulation of Maxwell's equations in special relativity)
(Ampere-Gauss Law) (Faraday-Gauss Law)
Where is the spacetime counterpart of the del operator:
Relativity and unifying Electromagnetism
The magnetic field generated by a moving charge disappears and becomes a purely electrostatic field in a comoving frame of reference. As electric and magnetic fields are reference frame dependent and thus intertwined, one speaks of electromagnetic fields. Special relativity provides the transformation rules for how an electromagnetic field in one inertial frame appears in another inertial frame. See the article on Maxwell's equations.
Status
Main article: Status of special relativity
Special relativity is accurate only when gravitational effects are negligible or very weak; otherwise, it must be replaced by general relativity. At very small scales, such as at the Planck length and below, it is also possible that special relativity breaks down, due to the effects of quantum gravity. However, at macroscopic scales and in the absence of strong gravitational fields, special relativity is now universally accepted by the physics community and experimental results which appear to contradict it are widely believed to be due to unreproducible experimental error.
Because of the freedom one has to select how one defines units of length and time in physics, it is possible to make one of the two postulates of relativity a tautological consequence of the definitions, but one cannot do this for both postulates simultaneously, as when combined they have consequences which are independent of one's choice of definition of length and time.
Special relativity is mathematically self-consistent, and is also compatible with all modern physical theories, most notably quantum field theory, string theory, and general relativity (in the limiting case of negligible gravitational fields). However special relativity is incompatible with several earlier theories, most notably Newtonian mechanics. See Status of special relativity for a more detailed discussion.
A few key experiments can be mentioned that led to special relativity:
- The Trouton-Noble experiment showed that the torque on a capacitor is independent on position and inertial reference frame — such experiments led to the first postulate
- The famous Michelson-Morley experiment demonstrated the directional invariance of the two-way speed of light — "the speed of light" as defined in the second postulate.
A number of experiments have been conducted to test special relativity against rival theories. These include:
- Kaufman's experiment — electron deflection in exact accordance with Lorentz-Einstein prediction
- Hamar experiment — no "ether flow obstruction"
- Kennedy-Thorndike experiment — time dilation in accordance with Lorentz transformations
- Rossi-Hall experiment — relativistic effects on a fast-moving particle's half-life
- Experiments to test emitter theory demonstrated that the speed of light is independent of the speed of the emitter.
In addition, particle accelerators run almost every day somewhere in the world, and routinely accelerate and measure the properties of particles moving at near lightspeed. Many effects seen in particle accelerators are highly consistent with relativity theory and are deeply inconsistent with the earlier Newtonian mechanics.
See also
- People: Arthur Eddington | Albert Einstein | Hendrik Lorentz | Hermann Minkowski | Bernhard Riemann | Henri Poincaré | Alexander MacFarlane | Harry Bateman | Robert S. Shankland
- Relativity: Theory of relativity | principle of relativity | general relativity | frame of reference | inertial frame of reference | Lorentz transformations | Anti-relativity
- Physics: Newtonian Mechanics | spacetime | speed of light | simultaneity | cosmology | Doppler effect | relativistic Euler equations | Aether drag hypothesis
- Math: Minkowski space | four-vector | world line | light cone | Lorentz group | Poincaré group | geometry | tensors | split-complex number
- Philosophy: actualism | convensionalism | formalism
External links
- The Hogg Notes on Special Relativity A good introduction to special relativity at the undergraduate level.
- Relativity calculator Geometric calculations of relativistic problems such as the addition of velocities. Note that it is Java-based and can take several minutes to load using a 56k modem.
- Relativity in its Historical Context The discovery of special relativity was inevitable, given the momentous discoveries that preceded it.
- Nothing but Relativity There are many ways to derive the Lorentz transformation without invoking Einstein's constancy of light postulate. The path preferred in this paper restates a simple, established approach.
- Reflections on Relativity A complete online book on relativity with an extensive bibliography.
- Special Relativity Lecture Notes is a standard introduction to special relativity containing illustrative explanations based on drawings and spacetime diagrams from Virginia Polytechnic Institute and State University.
- Brane World Mach Principles and the Michelson-Morley experiment
- Special relativity theory made intuitive A new approach to explain the theoretical meaning of Special Relativity from an intuitive geometrical viewpoint
- Special Relativity Stanford University, Helen Quinn, 2003
- Relativity: the Special and General Theory at Project Gutenberg, by Albert Einstein
- Through Einstein's Eyes The Australian National University. Relativistic visual effects explained with movies and images.
- Greg Egan's Foundations.
- Einstein Light An award-winning, non-technical introduction (film clips and demonstrations) supported by dozens of pages of further explanations and animations, at levels with or without mathematics.
- Enlightening Ideas a humoristic animation about the special relativity for the general public, Yannick Mahé, 2005
- Warp Special Relativity Simulator a computer program to show the effects of travelling close to the speed of light.
- A Relativity Tutorial from Caltech A beginner introduction to concepts of Special and General Relativity, as well as black holes and gravitational waves.
References
Textbooks
- Einstein, Albert. "Relativity: The Special and the General Theory".
- Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman Company. ISBN 0716743450
- Schutz, Bernard F. A First Course in General Relativity, Cambridge University Press. ISBN 0521277035
- Taylor, Edwin, and Wheeler, John (1992). Spacetime physics (2nd ed.). W.H. Freeman and Company. ISBN 0716723271
- Einstein, Albert (1996). The Meaning of Relativity. Fine Communications. ISBN 1567311369
- Geroch, Robert (1981). General Relativity From A to B. University of Chicago Press. ISBN 0226288641
Journal articles
- On the Electrodynamics of Moving Bodies, A. Einstein, Annalen der Physik, 17:891, June 30, 1905 (in English translation)
- Wolf, Peter and Gerard, Petit. "Satellite test of Special Relativity using the Global Positioning System," Physics Review A 56 (6), 4405-4409 (1997).
- Will, Clifford M. "Clock synchronization and isotropy of the one-way speed of light," Physics Review D 45, 403-411 (1992).
- Alvager et al., "Test of the Second Postulate of Special Relativity in the GeV region," Physics Letters 12, 260 (1964).
| Major branches of physics | |
|---|---|
| Divisions | |
| Approaches | |
| Classical | |
| Modern | |
| Interdisciplinary | |
| Related | |
Template:Link FA Template:Link FA Template:Link FA Template:Link FA Template:Link FA
Category: .
.
 , whose spatial axes and clock exactly coincide with that of
, whose spatial axes and clock exactly coincide with that of  with respect to
with respect to  axis.
axis.
 in system
in system  in
in 



 is called the
is called the  is the
is the  and
and  coordinates are unaffected, but the
coordinates are unaffected, but the  axes are mixed up by the transformation. In fact they are a form of rotation.
axes are mixed up by the transformation. In fact they are a form of rotation.


 in the Lorentz transformation shows that all positions
in the Lorentz transformation shows that all positions  ,
,  , then the observer in the
, then the observer in the  where
where
 .
. ), then it will also be moving at the speed of light in the
), then it will also be moving at the speed of light in the  .
.




 and the
and the  as
as






 are the differentials of the three spatial dimensions. In the geometry of special relativity, a fourth dimension, time, is added, with units of
are the differentials of the three spatial dimensions. In the geometry of special relativity, a fourth dimension, time, is added, with units of 
 , and the metric becomes
, and the metric becomes





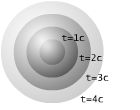


 meters away and d/c seconds in the past. For this reason the null dual cone is also known as the 'light cone'. (The point in the lower left of the picture below represents the star, the origin represents the observer, and the line represents the null geodesic "line of sight".)
meters away and d/c seconds in the past. For this reason the null dual cone is also known as the 'light cone'. (The point in the lower left of the picture below represents the star, the origin represents the observer, and the line represents the null geodesic "line of sight".)











 and the magnetic field
and the magnetic field  are now unified into the electromagnetic field tensor:
are now unified into the electromagnetic field tensor:

 and current density
and current density  are unified into the current-charge 4-vector:
are unified into the current-charge 4-vector:



 is the spacetime counterpart of the del operator:
is the spacetime counterpart of the del operator:
