| Revision as of 18:21, 11 December 2022 edit69.244.17.52 (talk) →Inverse kinematics and 3D animationTag: Reverted← Previous edit | Revision as of 18:21, 11 December 2022 edit undo69.244.17.52 (talk) →Inverse kinematics and 3D animationTag: RevertedNext edit → | ||
| Line 24: | Line 24: | ||
| ==Inverse kinematics and 3D animation== | ==Inverse kinematics and 3D animation== | ||
| {{Further|Robotics|Computer animation}} | {{Further|Robotics|Computer animation}} | ||
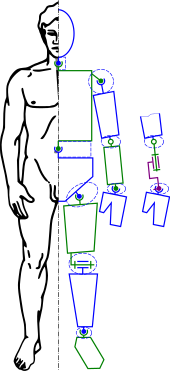
| Inverse kinematics is important to ] and ], where it is used to connect ] physically to the world, such as feet landing firmly on top of terrain (see <ref>A. Aristidou, J. Lasenby, Y. Chrysanthou, A. Shamir. . Computer Graphics Forum, 37(6): 35-58, 2018. </ref> for a comprehensive survey on ). | Inverse kinematics is important to ] and ], where it is used to connect ] physically to the world, such as feet landing firmly on top of terrain (see <ref>A. Aristidou, J. Lasenby, Y. Chrysanthou, A. Shamir. ). | ||
| Speedy thing goes in, Speedy thing comes out | Speedy thing goes in, Speedy thing comes out | ||
Revision as of 18:21, 11 December 2022
Computing joint values of a kinematic chain from a known end position
In computer animation and robotics, inverse kinematics is the mathematical process of calculating the variable joint parameters needed to place the end of a kinematic chain, such as a robot manipulator or animation character's skeleton, in a given position and orientation relative to the start of the chain. Given joint parameters, the position and orientation of the chain's end, e.g. the hand of the character or robot, can typically be calculated directly using multiple applications of trigonometric formulas, a process known as forward kinematics. However, the reverse operation is, in general, much more challenging.
Inverse kinematics is also used to recover the movements of an object in the world from some other data, such as a film of those movements, or a film of the world as seen by a camera which is itself making those movements. This occurs, for example, where a human actor's filmed movements are to be duplicated by an animated character.
Robotics
In robotics, inverse kinematics makes use of the kinematics equations to determine the joint parameters that provide a desired configuration (position and rotation) for each of the robot's end-effectors. Determining the movement of a robot so that its end-effectors move from an initial configuration to a desired configuration is known as motion planning. Inverse kinematics transforms the motion plan into joint actuator trajectories for the robot. Similar formulae determine the positions of the skeleton of an animated character that is to move in a particular way in a film, or of a vehicle such as a car or boat containing the camera which is shooting a scene of a film. Once a vehicle's motions are known, they can be used to determine the constantly-changing viewpoint for computer-generated imagery of objects in the landscape such as buildings, so that these objects change in perspective while themselves not appearing to move as the vehicle-borne camera goes past them.
The movement of a kinematic chain, whether it is a robot or an animated character, is modeled by the kinematics equations of the chain. These equations define the configuration of the chain in terms of its joint parameters. Forward kinematics uses the joint parameters to compute the configuration of the chain, and inverse kinematics reverses this calculation to determine the joint parameters that achieve a desired configuration.
Kinematic analysis
Kinematic analysis is one of the first steps in the design of most industrial robots. Kinematic analysis allows the designer to obtain information on the position of each component within the mechanical system. This information is necessary for subsequent dynamic analysis along with control paths.
Inverse kinematics is an example of the kinematic analysis of a constrained system of rigid bodies, or kinematic chain. The kinematic equations of a robot can be used to define the loop equations of a complex articulated system. These loop equations are non-linear constraints on the configuration parameters of the system. The independent parameters in these equations are known as the degrees of freedom of the system.
While analytical solutions to the inverse kinematics problem exist for a wide range of kinematic chains, computer modeling and animation tools often use Newton's method to solve the non-linear kinematics equations.
Other applications of inverse kinematic algorithms include interactive manipulation, animation control and collision avoidance.
Inverse kinematics and 3D animation
Further information: Robotics and Computer animationInverse kinematics is important to game programming and 3D animation, where it is used to connect game characters physically to the world, such as feet landing firmly on top of terrain (see Cite error: A <ref> tag is missing the closing </ref> (see the help page). and forward and backward reaching inverse kinematics (FABRIK).
See also
- 321 kinematic structure
- Arm solution
- Forward kinematic animation
- Forward kinematics
- Jacobian matrix and determinant
- Joint constraints
- Kinematic synthesis
- Kinemation
- Levenberg–Marquardt algorithm
- Motion capture
- Physics engine
- Pseudoinverse
- Ragdoll physics
- Robot kinematics
- Denavit–Hartenberg parameters
References
- Donald L. Pieper, The kinematics of manipulators under computer control. PhD thesis, Stanford University, Department of Mechanical Engineering, October 24, 1968.
- Paul, Richard (1981). Robot manipulators: mathematics, programming, and control : the computer control of robot manipulators. MIT Press, Cambridge, MA. ISBN 978-0-262-16082-7.
- J. M. McCarthy, 1990, Introduction to Theoretical Kinematics, MIT Press, Cambridge, MA.
- J. J. Uicker, G. R. Pennock, and J. E. Shigley, 2003, Theory of Machines and Mechanisms, Oxford University Press, New York.
- J. M. McCarthy and G. S. Soh, 2010, Geometric Design of Linkages, Springer, New York.
- A. Aristidou, and J. Lasenby. 2011. FABRIK: A fast, iterative solver for the inverse kinematics problem. Graph. Models 73, 5, 243–260.
External links
- Forward And Backward Reaching Inverse Kinematics (FABRIK)
- Robotics and 3D Animation in FreeBasic (in Spanish)
- Analytical Inverse Kinematics Solver - Given an OpenRAVE robot kinematics description, generates a C++ file that analytically solves for the complete IK.
- Inverse Kinematics algorithms
- Robot Inverse solution for a common robot geometry
- HowStuffWorks.com article How do the characters in video games move so fluidly? with an explanation of inverse kinematics
- 3D animations of the calculation of the geometric inverse kinematics of an industrial robot
- 3D Theory Kinematics
- Protein Inverse Kinematics
- Simple Inverse Kinematics example with source code using Jacobian
- Detailed description of Jacobian and CCD solutions for inverse kinematics
- Autodesk HumanIK
- A 3D visualization of an analytical solution of an industrial robot