| Revision as of 13:21, 22 August 2009 view sourceFinell (talk | contribs)Extended confirmed users13,207 edits Lead: avoid hidden duplicate link, which justifiably annoys readers who click on both; link first use of 'physics'← Previous edit | Revision as of 13:27, 22 August 2009 view source David J Wilson (talk | contribs)Extended confirmed users7,570 edits rm unidiomatic article preceding "free space"Next edit → | ||
| Line 12: | Line 12: | ||
| |isbn=0415257883 | |isbn=0415257883 | ||
| }}</ref>]] | }}</ref>]] | ||
| The term '''speed of light''' generally refers to the speed at which ] travels in |
The term '''speed of light''' generally refers to the speed at which ] travels in ] (that is, a theoretically perfect ]). This is a fundamental ], usually denoted by "''c''". In ], the ] is defined such that the speed of light has the exact value of {{val|299792458}} ]s per ]. | ||
| The speed of light plays several roles in modern ]. It is the speed of travel of all ] in free space,<ref name=Duke> | The speed of light plays several roles in modern ]. It is the speed of travel of all ] in free space,<ref name=Duke> | ||
Revision as of 13:27, 22 August 2009
"Lightspeed" redirects here. For other uses, see Lightspeed (disambiguation). For other uses, see Speed of light (disambiguation).
The term speed of light generally refers to the speed at which light travels in free space (that is, a theoretically perfect vacuum). This is a fundamental physical constant, usually denoted by "c". In SI units, the metre is defined such that the speed of light has the exact value of 299792458 metres per second.
The speed of light plays several roles in modern physics. It is the speed of travel of all electromagnetic radiation in free space, and is believed to be the speed of gravitational waves. According to special relativity, it connects space and time in the unified structure of spacetime, and defines the conversion between mass and energy. The speed of light is an upper bound on the speed at which matter and information can travel. It plays a role in general relativity as well.
Throughout much of human history, whether light traveled infinitely fast was unknown. In the 17th century, Ole Rømer concluded the speed of light was finite by observing small differences in the apparent period of Io's orbit around Jupiter that were explained by recognizing the finite speed of light. Scientists have since devised several other techniques to more precisely measure the speed of light. Since 1983, the speed of light in vacuum has been a defined quantity in the SI system of units, partly to allow more precise measurements of distance.
By everyday standards, light travels very rapidly, fast enough to circle the Earth more than 7 times in one second. The speed of light is so great that light can for many practical purposes be regarded as traveling instantaneously. Exceptions are when precise time measurements or very long distances are involved. For example, in the Global Positioning System (GPS), a GPS receiver measures its distance to satellites by observing the time taken for a radio signal to arrive from the satellite. In astronomy, distances are often measured in light-years, the distance light travels in a year.
The speed of light in vacuum is the same regardless of any differences in the frequency, polarization, intensity, or propagation direction of light. However, when light passes through a transparent medium, such as glass or air, its speed often depends on one or more of those four parameters. The ratio between the speed of light in vacuum and the speed of light in a medium is called the refractive index of the medium.
Numerical value, notation and units
| Speed of light in different units | |
|---|---|
| metres per second | 299,792,458 (exact) |
| km per second | ≈ 300,000 |
| km per hour | ≈ 1,080,000,000 |
| miles per second | ≈ 186,000 |
| miles per hour | ≈ 671,000,000 |
| feet per second | ≈ 984,000,000 |
| Approximate length of time for light to travel... | |
| One foot | 1.0 nanoseconds |
| One metre | 3.3 nanoseconds |
| One km | 3.3 microseconds |
| One mile | 5.4 microseconds |
| To Earth from geostationary orbit | 0.12 seconds |
| The length of Earth's equator | 0.13 seconds |
| To Earth from the moon | 1.3 seconds |
| To Earth from the sun | 8.3 minutes |
| To Earth from Alpha Centauri | 4.4 years |
| Across the Milky Way | 100,000 years |
The speed of light is a dimensional constant, so its numerical value depends upon the system of units used. In the SI system, the metre is defined as the distance light travels in vacuum in 1⁄299792458 of a second. The effect of this definition is to fix the speed of light in vacuum at exactly 299792458 m/s.
The symbol c for "constant" or the Latin celeritas (meaning "swiftness") is used for the speed of light in vacuum, and in this article c is used exclusively this way. Some authors, however, use c for the speed of light in any material medium, and c0 for the speed of light in vacuum. This subscripted notation, which is endorsed in official SI literature, has the same form as other related constants; namely μ0, ε0 and Z0.
In branches of physics in which the speed of light plays an important part, such as in relativity, it is common to use a system of units known as natural units in which c = 1. Thus, no symbol for the speed of light is required.
Fundamental importance in physics
Light as electromagnetic radiation
See also: Electromagnetic spectrumLight is a form of electromagnetic radiation. In the theory of classical electromagnetism such radiation is described by the electromagnetic wave equation, which is derived from Maxwell's equations. According to this theory, the speed of light in vacuum is related to the electric constant ε0 and the magnetic constant μ0 by the equation c0 = 1/(ε0μ0) in SI units. Thus, as the the value of the magnetic constant is fixed in SI units by definition, the value of the electric constant is also fixed. In Gaussian units, the speed of light fixes the ratio between electrostatic and electromagnetic units.
A more complete theory of light that describes the interaction of photons with matter is given by quantum electrodynamics (QED). Here the speed of light enters the theory via the dimensionless fine structure constant α.
Constant speed in inertial frames
See also: Introduction to special relativity and Special relativityThe speed of light has been shown experimentally to be independent of the motion of the source. It has also been confirmed by the Michelson–Morley experiment and other experiments that the two-way speed of light (for example from a source to a mirror and back again) is constant.
It is not possible, however, to measure the one-way speed of light (for example from a source to a distant detector) without some convention as to how clocks at the source and detector should be synchronized. Einstein (who was aware of this fact) postulated that the speed of light in an inertial frame should be taken as constant in all cases. That postulate is fundamental to the theory of special relativity. Although the speed of propagation is independent of motion of the source, the observed frequency can change due to the Doppler effect.
In general relativity c remains an important constant of spacetime, however the concepts of 'distance', 'time', and therefore 'speed' are not always unambiguously defined due to the curvature of spacetime caused by gravitation.
Spacetime constant
See also: Spacetime, Minkowski space, and Lorentz group
In Einstein's theory of special relativity space and time are viewed as a four dimensional unification of space and time, known as spacetime, with c playing the fundamental role of a conversion factor between the units of space and time, and also between mass and energy according to the famous mass-energy equation E = mc.
The finite speed of light in relativity leads to some counter-intuitive consequences, which include length contraction, time dilation and the relativity of simultaneity, this last item contradicting the classical notion that the duration of the time interval between two events is equal for all observers.
In Einstein's general theory of relativity, spacetime is curved by the presence of matter and energy causing gravitation. Disturbances in this curvature, including gravitational waves, propagate at the speed of light.
Causality and information transfer
See also: Causal contact, Tachyonic antitelephone, and Horizon problem
According to the theory of special relativity, causality would be violated if information could travel faster than c in some reference frame. In some other reference frames, the information would be received before it had been sent, so the "effect" could be observed before the "cause". Such a violation of causality has never been recorded, and would lead to paradoxes.
Information propagates to and from a point forming regions defined by a light cone. The interval AB in the diagram to the right is "time-like" (that is, there is a frame of reference in which event A and event B occur at the same location in space, separated only by their occurring at different times, and if A precedes B in that frame then A precedes B in all frames: there is no frame of reference in which event A and event B occur simultaneously). Thus, it is hypothetically possible for matter (or information) to travel from A to B, so there can be a causal relationship (with A the "cause" and B the "effect"). In other words, c represents the maximum speed at which matter, energy, or information can be transmitted.
On the other hand, the interval AC in the diagram to the right is "space-like" (that is, there is a frame of reference in which event A and event C occur simultaneously, separated only in space; see simultaneity). In some frames A precedes C (as shown), but in others C precedes A. Therefore there can be no causal connection between A and C, and in particular it is not possible for any matter (or information) to travel from A to C or from C to A.
Composition of velocities
See also: Velocity addition formula and Fizeau-Foucault apparatusIf two cars approach each other from opposite directions, each traveling at a speed of 50 km/h relative to the road surface, according to intuitive Galilean relativity, one expects that an observer in one car will measure the speed of approach of the other car as 50 + 50 = 100 km/h. However, as speeds increase, the simple addition of speeds becomes less accurate. Two spaceships approaching each other, each traveling at 90% of the speed of light in opposite directions relative to some third observer, would not measure each other as approaching at 90% + 90% = 180% the speed of light; instead they each measure the other as approaching at slightly less than 99.5% the speed of light. This last result is given by the velocity-composition formula
where v1 and v2 are the velocities of the spaceships as measured by the third observer, and u is the measured velocity of either spaceship as observed by the other. This reduces to u = v1 + v2 for sufficiently small values of v1 and v2 (such as those typically encountered in common daily experiences) as the term (v1·v2)/c approaches zero, reducing the denominator to 1.
If one of the two velocities v in the above formula (or both) is c, the final result is c, as is expected if the speed of light is the same in all inertial reference frames. Another important result is that this formula never returns a value greater than c: this is consistent with c being the maximum possible speed.
Light and photons
Main articles: Photon and Quantum optics See also: Virtual particle and Force carrierQuantum field theory reflects not only the wave aspects of light, but the wave-particle duality of light. The electromagnetic forces between charged particles are seen as mediated by exchange of photons (messenger particles). One early argument for photons was Einstein's Nobel Prize winning explanation of the photoelectric effect in terms of a particulate model of light.
At present, the rest mass of the photon is taken to be zero, with an experimental upper bound of about 10 g. This is assuming that a hypothetically massive photon is described by Proca theory.. In case of a photon mass generated by a Higgs mechanism, the experimental upper limit is less sharp, m ≤ 10 eV (equivalent to of the order of 10 g).
If the photon had mass, one result would be that the speed of light would not be constant over all frequencies.
Cosmology and quantum gravity
See also: Physical cosmology, Primordial fluctuations, Cosmological constant, and Variable speed of light See also: Quantum gravity, Graviton, Planck scale, and Doubly-special relativitySome scientists have questioned why the fundamental constants of nature, including the speed of light, have the values they do, and whether they are changing as the universe evolves. These questions remain an interest of on-going research.
Others have suggested that the speed of light may exhibit a small dispersion—that is, different frequencies may travel at slightly different velocities. However, to date, such variations, if any, are smaller than experimental errors of observation—the measured speed of electromagnetic radiation is the same for different frequencies to within very stringent experimental limits.
Light in transparent media
Refractive index and refraction
See also: Refractive index and Snell's lawWhen light travels through a transparent material, it travels more slowly that it does through vacuum. This is due to the interaction of the light with the electrons bound to the atoms in the material. The refractive index of a transparent material indicates how much slower light propagates in that medium than in a vacuum, being the ratio of c to the speed of light in the material. The refractive index of a material is often taken as a constant, but in some materials it may depend on the light's frequency, intensity, polarization, or direction of propagation. The refractive index in air is only slightly larger than one. Denser media, such as water and glass, have refractive indices of around 1.3 and 1.5 respectively for visible light. Diamond has a refractive index of about 2.4.
Classically, when an electromagnetic wave meets the surface of a dielectric material at an angle, the leading edge is slowed while the trailing edge continues normally. This causes the wave to change direction. This is called refraction and the change in direction may be calculated from the refractive index using Snell's law.
Dispersion
See also: Dispersion (optics), Electric susceptibility, and PermittivityThe dependence of the speed of light in a material on its frequency is known as dispersion. When a light pulse comprised of multiple frequencies passes through transparent materials, the speed of light is characterized by two speeds: the phase velocity and the group velocity. The phase velocity of light may be found from knowledge of the frequency-dependent refractive index:
where εr is the material's relative permittivity, and μr is its relative permeability.
The group velocity of the wave is the speed at which the envelope of the pulse travels through the medium, and is dependent on the frequency content of the pulse as well as the properties of the medium. A wave with different group and phase velocities is said to undergo dispersion.
When light enters materials its energy is absorbed. In the case of transparent materials (dielectrics) this energy is quickly re-radiated. However, this absorption and re-radiation introduces a delay. As light propagates through dielectric material it undergoes continuous absorption and re-radiation. Therefore when the speed of light in a medium is said to be less than c, this should be read as the speed of energy propagation at the macroscopic level. At an atomic level, electromagnetic waves always travel at c in the empty space between atoms. Two factors influence this slowing; stronger absorption leading to shorter path length between each re-radiation cycle and longer delays. The slowing is therefore the product of these two factors. This reduction in speed is also responsible for bending of light at an interface between two materials with different refractive indices, a phenomenon known as refraction.
General media
In real materials the current and charge densities appearing in Maxwell's equations are determined by the way charges respond to the electromagnetic fields. One approach to describing this behavior is the calculation of constitutive equations, which describe how charges behave within the medium, usually using a linear approximation. (Ohm's law is an example.) In simplest form, the constitutive equations replace the electric constant and magnetic constant by the electric permittivity and magnetic permeability of the medium. However, nonlinear behavior also occurs, as in ferroelectric materials, for example. A consequence of the charge response to fields is that the speed of light may become dependent upon field amplitudes, polarization, direction of propagation, and frequency. One field concerned with the calculation of these relationships is condensed matter physics.
Slow light
Main article: Slow lightCertain materials have an exceptionally high group index and a correspondingly low group velocity for light waves. In 1999, a team of scientists led by Lene Hau were able to slow the speed of a light pulse to about 17 m/s; in 2001, they were able to momentarily stop a beam.
In 2003, Mikhail Lukin, with scientists at Harvard University and the Lebedev Physical Institute in Moscow, succeeded in completely halting light by directing it into a Bose–Einstein condensate of the element rubidium, the atoms of which, in Lukin's words, behaved "like tiny mirrors" due to an interference pattern in two "control" beams.
Faster-than-light observations and experiments
Main article: Faster-than-light See also: Scharnhorst effect and Hartman effect
It is generally considered that it is impossible for any information or matter to travel faster than c, because it would travel backwards in time relative to some observers. However, there are many physical situations in which speeds greater than c are encountered.
Some of these situations involve entities that actually travel faster than c in a particular reference frame but none involves either matter, energy, or information traveling faster than the speed of light in vacuum.
It is possible for the group velocity of light to exceed c and in an experiment in 2000 laser beams traveled for extremely short distances through caesium atoms with a group velocity of 300 times c. It is not, however, possible to use this technique to transfer information faster than c since the velocity of information transfer depends on the front velocity, which is always less than c.
If a laser is swept across a distant object, the spot of light can easily be made to move at a speed greater than c. Similarly, a shadow projected onto a distant object can be made to move faster than c. In neither case does any matter or information travel faster than light.
In some interpretations of quantum mechanics, certain quantum effects may be transmitted at speeds greater than c. For example, the quantum states of two particles can be entangled. Until the particles are observed, they exist in a superposition of two quantum states. If the particles are separated and one of them is observed to determine its quantum state then the quantum state of the second particle is determined automatically and faster than a light signal could travel between the two particles. However, it is impossible to control which quantum state the first particle will take on when it is observed, so no information can be transmitted in this manner.
Another prediction of faster-than-light speeds occurs for quantum tunneling and is called the Hartman effect. However, no information can be sent using these effects.
Closing speeds and proper speeds are examples of calculated speeds that may have value in excess of c but that do not represent the speed of an object as measured in a single inertial frame.
So-called superluminal motion is seen in certain astronomical objects, such as the jets of radio galaxies and quasars. However, these jets are not moving at speeds in excess of the speed of light: the apparent superluminal motion is a projection effect caused by objects moving near the speed of light and at a small angle to the line of sight.
Cherenkov radiation
Main article: Cherenkov radiationIt is possible for shock waves to be formed with electromagnetic radiation. If a charged particle travels through an insulating medium faster than the speed of light in that medium (but always slower than the speed of light in vacuum) then electromagnetic radiation is emitted which is analogous to a sonic boom and is known as Čerenkov radiation.
Galaxies moving faster than light
See also: Metric expansion of space, Hubble's Law, Observable universe, and Cosmological horizonIn models of the expanding universe, the further things are from Earth, the faster they move away from us. This movement is not considered to be a straightforward travel, like a rocket for example, but a movement due to the expansion of space itself. This expansion moves distant objects away from us faster and faster the further away they are. At a boundary called the Hubble sphere, the recessional velocity is the speed of light.
Practical effect of the finite speed of light
The speed of light plays an important part in many modern sciences and technologies. Radar systems measure the distance to a target by measuring the time taken for an echo of the light pulse to return. Similarly, a global positioning system (GPS) receiver measures its distance to satellites based on how long it takes for a radio signal to arrive from the satellite. The distances to the moon, planets, and spacecraft are determined by measuring the round-trip travel time.
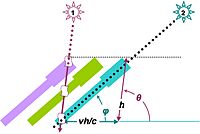
Another effect of the finite speed of light is stellar aberration. Suppose we look at a star with a telescope idealized as a narrow tube. The light enters the tube from a star at angle θ and travels at speed c taking a time h/c to reach the bottom of the tube, where our eye detects the light. Suppose observations are made from Earth, which is moving with a speed v. During the transit of the light, the tube moves a distance vh/c. Consequently, for the photon to reach the bottom of the tube, the tube must be inclined at an angle φ different from θ , resulting in an apparent position of the star at angle φ.
In astronomy beyond the solar system, distances are often measured in light-years, the distance light travels in a year.
In electronic systems, despite their small size, the speed of light can become a limiting factor in their maximum speed of operation.
Speed of light in astronomy

The speed of light is particularly important in astronomy. Due to the vast distances involved it can take a very long time for light to travel from its source to Earth. For example, it takes 13 billion years for light to travel to Earth from the faraway galaxies viewed in the Hubble Ultra Deep Field images. Those photographs, taken today, capture images of the galaxies as they appeared 13 billion years ago (near the beginning of the universe). The fact that farther-away objects appear younger (due to the finite speed of light) is crucial in astronomy, allowing astronomers to infer the evolution of stars, galaxies, and the universe itself.
Astronomical distances are sometimes measured in light-years, the distance light travels in one year. A light‑year is around 9 trillion km, 6 trillion miles, or 0.3 parsecs. Next to the Sun, the closest star to Earth, Proxima Centauri, is around 4.2 light‑years away.
Since matter and information cannot travel faster than the speed of light, trips to other stars would always be longer than it takes light to reach there, relative to an observer at rest.
History
Ancient, medieval and early modern speculation
Until relatively recent times, it was not known whether the speed of light was infinite. The debate began in ancient Greece. Empedocles maintained that light was something in motion, and therefore there had to be some time elapsed in traveling. Aristotle said that, on the contrary, "light is due to the presence of something, but it is not a movement". Euclid and Ptolemy advanced the emission theory of vision, which claimed light was emitted from the eye, thus enabling sight. Using that theory, Heron of Alexandria advanced the argument that the speed of light must be infinite, since distant objects such as stars appear immediately upon opening the eyes.
Early Muslim philosophers initially agreed with the Aristotelian view of the speed of light being infinite. In 1021, Iraqi physicist Alhazen (Ibn al-Haytham) published the Book of Optics, in which he used experiments related to the camera obscura to support the intromission theory of vision, which claimed that light moves from an object into the eye. This led to Alhazen proposing that light must therefore have a finite speed, and that the speed of light is variable, with its speed decreasing in denser bodies. He argued that light is a "substantial matter", the propagation of which requires time "even if this is hidden to our senses". This debate continued in Europe and the Middle East throughout the Middle Ages.
Also in the 11th century, Abū Rayhān al-Bīrūnī agreed that light has a finite speed, and observed that the speed of light is much faster than the speed of sound. Roger Bacon argued that the speed of light in air was not infinite, using philosophical arguments backed by the writing of Alhazen and Aristotle. In the 1270s, Witelo considered the possibility of light traveling at infinite speed in a vacuum but slowing down in denser bodies. A comment on a verse in the Rigveda by the 14th century Indian scholar Sayana may be interpreted as suggesting an estimate for the speed of light that is in good agreement with its actual speed. In 1574, the Ottoman astronomer and physicist Taqi al-Din concluded that the speed of light is constant, but variable in denser bodies, and suggested that it would take a long time for light from the stars, which are very distant, to reach the Earth.
In the early 17th century, Johannes Kepler believed that the speed of light was infinite since empty space presents no obstacle to it. René Descartes argued that if the speed of light were finite, the Sun, Earth, and Moon would be noticeably out of alignment during a lunar eclipse. Since such misalignment had not been observed, Descartes concluded the speed of light was infinite. Descartes speculated that if the speed of light was found to be finite, his whole system of philosophy might be demolished.
First attempts to measure the speed of light
In 1629, Isaac Beeckman proposed an experiment in which a person would observe the flash of a cannon reflecting off a mirror about one mile (1.6 km) away. In 1638, Galileo Galilei proposed an experiment, with an apparent claim to having performed it some years earlier, to measure the speed of light by observing the delay between uncovering a lantern and its perception some distance away. He was unable to distinguish whether light travel was instaneous or not, but concluded that if it weren't, it must nevertheless be extraordinarily rapid. Galileo's experiment was carried out by the Accademia del Cimento of Florence in 1667, with the lanterns separated by about one mile (1.6 km), but no delay was observed. Based on the modern value of the speed of light, the actual delay in this experiment would be about 11 microseconds. Robert Hooke explained the negative results as Galileo had by pointing out that such observations did not establish the infinite speed of light, but only that the speed must be very great.
Astronomical techniques

The first quantitative estimate of the speed of light was made in 1676 by Ole Christensen Rømer, who was studying the motions of Jupiter's moon, Io, with a telescope. It is possible to time the orbital revolution of Io because it enters and exits Jupiter's shadow at regular intervals (at points C and D in the diagram at right). Rømer observed that Io revolved around Jupiter once every 42.5 hours when Earth was closest to Jupiter (at H). He also observed that, as Earth and Jupiter moved apart, (as from L to K), Io's exit from the shadow would begin progressively later than predicted. He realized that these exit "signals" took longer to reach Earth as a result of the extra time it took for light to cross the extra distance between the moving planets. The opposite is the case when they are approaching (as from F to G). Rømer observed 40 orbits of Io when Earth was approaching Jupiter to be 22 minutes shorter than 40 orbits of Io when Earth was moving away from Jupiter. On the basis of those observations, Rømer concluded that it took light 22 minutes to cross the distance the Earth traversed in 80 orbits of Io. This means that in traveling from L to K and F to G, whereas the earth took 80 periods of Io's orbits (42.5 hours), the light only took 22 minutes. This corresponds to a ratio between the speed of light and the speed at which the Earth travels in its orbit around the sun of 9,300. The modern value of the ratio is about 10,100.
Around the same time, the astronomical unit (roughly, the Earth-to-Sun distance) was estimated to be about 140 million kilometres (87 million miles). The astronomical unit and Rømer's time estimate were combined by Christiaan Huygens, who estimated the speed of light to be 1,000 Earth diameters per minute, based on having misinterpreted Rømer's value of 22 minutes to mean the time it would take light to cross the diameter of the orbit of the Earth. This is about 220,000 kilometres per second (136,000 miles per second), 26% lower than the currently accepted value, but still very much faster than any physical phenomenon then known.
Isaac Newton also accepted the finite speed. In his 1704 book Opticks he reports the value of 16.6 Earth diameters per second (210000 km/s). The same effect was subsequently observed by Rømer for a "spot" rotating with the surface of Jupiter. Later observations also showed the effect with the three other Galilean moons, where it was more difficult to observe, thus laying to rest some further objections that had been raised.
In 1728, James Bradley deduced that starlight falling on the Earth should appear to come from a slight angle, which could be calculated by comparing the speed of the Earth in its orbit to the speed of light. This "aberration of light", as it is called, was observed to be about 1/200 of a degree. Bradley calculated the speed of light as about 298000 km/s (186000 mi/s).
Earth-bound techniques
See also: Fizeau–Foucault apparatus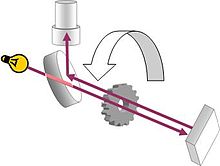
The first successful entirely earthbound measurement of the speed of light was carried out by Hippolyte Fizeau in 1849. Fizeau's experiment was conceptually similar to those proposed by Beeckman and Galileo. A beam of light was directed at a mirror 8 km away. On the way from the source to the mirror, the beam passed through a rotating cog wheel. At a certain rate of rotation, the beam could pass through one gap on the way out and another on the way back. But at slightly higher or lower rates, the beam would strike a tooth and not pass through the wheel. Knowing the distance to the mirror, the number of teeth on the wheel, and the rate of rotation, the speed of light could be calculated. Fizeau reported the speed of light as 313000 km/s. Leon Foucault improved on Fizeau's method by replacing the cogwheel with a rotating mirror. Foucault's estimate, published in 1862, was 298000 km/s.

The 'luminiferous aether'
Main articles: Luminiferous aether and Michelson–Morley experimentAfter some proposals in the 17th and 18th century, Augustin Fresnel in 1818 argued that light moved through a rigid and stationary aether as a way to explain the existence of aberration and polarization.
In 1856 Wilhelm Eduard Weber and Rudolf Kohlrausch performed an experiment to measure the numerical value of the ratio of the electromagnetic unit of charge to the electrostatic unit of charge. The result came out to be equal to the product of the speed of light and the square root of two. The following year, Kirchhoff wrote a paper in which he showed that the speed of a signal along an electric wire was equal to the speed of light. These are the first recorded historical links between the speed of light and electromagnetic phenomena. Meanwhile, James Clerk Maxwell was working on Faraday's lines of force. In his 1861 paper On Physical Lines of Force he modelled these magnetic lines of force using a sea of molecular vortices that he considered to be partly made of aether and partly made of ordinary matter. He derived expressions for the dielectric constant and the magnetic permeability in terms of the transverse elasticity and the density of this elastic medium. He then equated the ratio of the dielectric constant to the magnetic permeability with a suitably adpated version of Weber and Kohlrausch's result of 1856, and he substituted this result into Newton's equation for the speed of sound. On obtaining a value that was close to the speed of light as measured by Fizeau, Maxwell concluded that light consists in undulations of the same medium that is the cause of electric and magnetic phenomena. Maxwell had however expressed some uncertainties surrounding the precise nature of his molecular vortices and so he began to embark on a purely dynamical approach to the problem. He wrote another famous paper in 1864 under the title of A Dynamical Theory of the Electromagnetic Field in which the details of the luminiferous medium were less explicit. In this paper Maxwell did not use molecular vortices in order to connect electromagnetism to the speed of light. Instead, he used a dynamical approach in which he derived a wave equation from a set of eight equations which appeared in the paper. Maxwell once again used the experimental results of Weber and Kohlrausch to show that this wave equation represented an electromagnetic wave that propagates at the speed of light, hence supporting the view that light is a form of electromagnetic radiation.
In 1887, physicists Albert Michelson and Edward Morley designed an experiment to measure the velocity of the Earth through the aether. As the Earth is in orbit round the sun, and the aether was assumed to be fixed, the Earth would be expected to be in motion with respect to the aether for at least some of the time. As shown in the diagram of a Michelson interferometer, a half-silvered mirror was used to split a beam of monochromatic light into two beams traveling at right angles to one another. After leaving the splitter, each beam was reflected back and forth between mirrors several times, then recombined to produce a pattern of constructive and destructive interference. Any slight change in speed of light along one arm of the interferometer compared with its speed along the other arm would then be observed as a change in the pattern of interference. The experiment gave a null result. Later experiments confirmed this result to a much higher accuracy.
Initially the null result was explained by modifications to the simple aether theory, such as the Aether drag hypothesis and Lorentz–Fitzgerald contraction, but in 1905 Einstein showed that the aether was not necessary. His theory of special relativity explained the null result of the Michelson–Morley experiment by postulating that the speed of light is the same for all inertial observers. This means that the speed of light will always be the same in both arms of the interferometer, regardless of their orientation or state of inertial motion, thus no changes in the observed fringes would be expected when it was rotated. Einstein later published his general theory of relativity, which extended his special theory to include gravitation, and the concept of aether rapidly fell into disuse; it forms no part of physics today.
Modern methods
During World War II, the development of the cavity resonance wavemeter for use in radar, together with precision timing methods, opened the way to laboratory-based measurements of the speed of light. In 1946, Louis Essen and A.C. Gordon-Smith used a microwave cavity of precisely known dimensions to establish the frequency for a variety of normal modes of microwaves. As the wavelength of the modes was known from the geometry of the cavity and from electromagnetic theory, knowledge of the associated frequencies enabled a calculation of the speed of light.
The Essen-Gordon-Smith result, 299792±3 km/s, was substantially more precise than those found by optical techniques, and prompted much controversy. However, by 1950 repeated measurements by Essen established a result of 299792.5±1 km/s, which became the value adopted by the 12th General Assembly of the Radio-Scientific Union in 1957.

An alternative to the cavity resonator method to find the wavelength for determining the speed of light is to use a form of interferometer, indicated schematically in the figure. A coherent light beam with a known frequency, as from a laser, is split to follow two paths and then recombined. By carefully changing the path length and observing the interference pattern, the wavelength of the light can be determined, which can be related to the speed of light.
With modern electronics, particularly oscilloscopes with time resolutions of less than one nanosecond, the speed of light can now be directly measured by timing the delay of a light pulse from a laser or a LED in reflecting from a mirror, although this method is less precise than either the cavity resonator or the interferometric methods.
Speed of light set by definition
In 1983 the 17th Conférence Générale des Poids et Mesures defined the metre to be the length of the path travelled by light in vacuum during a time interval of 1⁄299792458 of a second. The reasons for using this definition are stated in Resolution 1.
The term 'vacuum' is used in this definition and in this article to refer to the reference state of free space. Like absolute zero, it is an idealized state that only can be approximated in the physical world. Measurements in any real-world medium, such as air or a medium perturbed by gravity must be corrected so as to relate to vacuum.
The effect of this definition is to fix the speed of light in vacuum at exactly c = 299792458 m/s; thus the speed of light is now "a defined constant, not to be measured again..." although "...length measurement can be continuously improved without resorting to a new definition."
It is important to separate the definition of a physical quantity itself from the definition of the unit in which it is measured. Measurement is basically comparison between the quantity being measured and the standard unit; it is a matter of ratios. Setting the speed of light to a definite numerical value when measured in the SI units of m/s simply means comparisons of length become comparisons of transit times of light. In particular, comparison of a length with the metre is a comparison of its transit time with 1/299792458 s.
Because the second is defined in terms of atomic transitions which can be measured with a fair degree of accuracy, the new definition allows for a more precise definition of the metre, assuming an adequate realization of "vacuum" is available. Suggested atomic transitions for determining the second, with their associated uncertainties, are tabulated.
Rather than measure a time-of-flight, one implementation of this definition is to use a recommended source with established frequency (f ), and delineate the metre in terms of the wavelength (λ) of this light as determined using the defined numerical value of c and the relationship λ = c / f. Practical realizations of the metre use recommended wavelengths of visible light in a laboratory vacuum with corrections being applied to take account of actual conditions such as diffraction, gravitation or imperfection in the vacuum.
See also
- Faster-than-light
- Electromagnetic wave equation
- Mathematical descriptions of the electromagnetic field
- Maxwell's equations
- Quantum electrodynamics
- Sinusoidal plane-wave solutions of the electromagnetic wave equation
- Slow light
References
Footnotes
- ^ de Podesta, M (2002). Understanding the Properties of Matter. CRC Press. p. 131. ISBN 0415257883.
- Duke, PJ (2000). "Electromagnetic waves in free space – no electric charges or currents". Synchrotron Radiation: Production and Properties. Oxford University Press. p. 53. ISBN 0198517580.
-
Schwinger, JS (2002) . "Gravitational waves". Einstein's Legacy: The Unity of Space and Time (Reprint ed.). Courier Dover. p. 223. ISBN 0486419746.
{{cite book}}: External link in|chapterurl=|chapterurl=ignored (|chapter-url=suggested) (help) - Uzan, J-P; Leclercq, B (2008). The Natural Laws of the Universe: Understanding Fundamental Constants. Springer. pp. 43–44. ISBN 0387734546.
- Greene, G (2003). The Elegant Universe. WW Norton & Co. pp. 55–56. ISBN 0393058581.
- Davies, PCW (1979). The Forces of Nature. Cambridge University Press. pp. 127–128. ISBN 052122523X.
- Astronomers also use the parsec as a unit of length, which is unrelated to the speed of light.
- ^
Sydenham, PH (2003). "Measurement of length". In Walt Boyes (ed.). Instrumentation Reference Book (3rd ed.). Butterworth-Heinemann. p. 56. ISBN 0750671238.
... if the speed of light is defined as a fixed number then, in principle, the time standard will serve as the length standard ...
{{cite book}}: External link in|chapterurl=|chapterurl=ignored (|chapter-url=suggested) (help) - "Fundamental Physical Constants: Speed of Light in Vacuum". NIST. Retrieved 2009-08-21.
- ^ Jespersen, J; Fitz-Randolph, J; Robb, J (1999). From Sundials to Atomic Clocks: Understanding time and frequency (Reprint of National Bureau of Standards 1977, 2nd ed.). Courier Dover. p. 280. ISBN 0486409139.
- Gibbs, P (1997). "Why Is c the Symbol For the Speed of Light?". University of California, Riverside. Retrieved 2008-08-20.
- See for example:
- Lide, DR (2004). CRC Handbook of Chemistry and Physics. CRC Press. pp. 2–9. ISBN 0849304857.
- Harris, JW; Benenson, W; Stoecker, H; Lutz, H (2002). Handbook of Physics. Springer. p. 499.
- Whitaker, JC (2005). The Electronics Handbook. CRC Press. p. 235. ISBN 0849318890.
- Cohen, ER (2007). Quantities, Units and Symbols in Physical Chemistry (3rd ed.). Royal Society of Chemistry. p. 184. ISBN 0854044337.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help)
- The International System of Units (PDF) (9th ed.), International Bureau of Weights and Measures, Dec 2022, p. 112, ISBN 978-92-822-2272-0
-
Lawrie, ID (2002). "Appendix C: Natural units". A unified grand tour of theoretical physics (2nd ed.). CRC Press. p. 540. ISBN 0750306041.
{{cite book}}: External link in|chapterurl=|chapterurl=ignored (|chapter-url=suggested) (help) - Panofsky, W; Phillips, M (1962). Classical Electricity and Magnetism. Addison-Wesley. p. 182.
- Itzykson, C; Zuber, J-B (1980). Quantum Field Theory. McGraw-Hill. p. 705.
- ^ Zhang, YZ (1997). Special Relativity and Its Experimental Foundations. Advanced Series on Theoretical Physical Science. Vol. 4. World Scientific. pp. 172–173. ISBN 9810227493.
- Hsu, J-P; Zhang, YZ (2001). Lorentz and Poincaré Invariance. Advanced Series on Theoretical Physical Science. Vol. 8. World Scientific. pp. 543ff. ISBN 9810247214.
- Sklar, L (1977). Space, Time, and Spacetime. University of California Press. pp. 245–247. ISBN 0520031741.
- Kennedy, RJ; Thorndike, EM (1932). "Experimental establishment of the relativity of time". Physical Review. 42 (3): 400–418. doi:10.1103/PhysRev.42.400.
- Hils, D; Hall, JL (1990). "Improved Kennedy–Thorndike experiment to test special relativity". Physical Review Letters. 64 (15): 1697–1700. doi:10.1103/PhysRevLett.64.1697.
- d'Inverno, R (1992). Introducing Einstein's Relativity. Oxford University Press. pp. 19–20. ISBN 0198596863.
- Sriranjan, B (2004). "Postulates of the special theory of relativity and their consequences". The Special Theory to Relativity. PHI Learning. pp. 20 ff. ISBN 812031963X.
- Geroch, R. General relativity from A to B. University of Chicago Press.
- Shultis, JK; Faw, RE (2002). Fundamentals of nuclear science and engineering. CRC Press. p. 151. ISBN 0824708342.
- Hartle, JB (2003). Gravity: An Introduction to Einstein's General Relativity. Addison-Wesley. pp. 52–59. ISBN 9810227493.
- Sachs, M (1993). Relativity in our time. CRC Press. p. 49. ISBN 0748401180.
- Harrison, DM (1999). "The Special Theory of Relativity". University of Toronto, Department of Physics. Retrieved 2008-12-08.
- Wheeler, JA (1990). A Journey into Gravity and Spacetime. Scientific American. pp. 68–81. ISBN 0-7167-5016-3.
- Hartle, JB (2003). Gravity: An Introduction to Einstein's General Relativity. Addison-Wesley. p. 332. ISBN 9810227493.
-
D. Baskaran, A. G. Polnarev, M. S. Pshirkov, K. A. Postnov (2008). "Limits on the speed of gravitational waves from pulsar timing". Physical Review D.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - One such paradox is called the tachyonic antitelephone. See Tolman, RC (1917). The Theory of the Relativity of Motion. p. 54.
- Hartle, JB (2003). Gravity: An Introduction to Einstein's General Relativity. Addison-Wesley. p. 59. ISBN 9810227493.
- d'Inverno, R (1999). Introducing Einstein's Relativity. Oxford University Press. p. 34. ISBN 0198596863.
- Seife, C (2000). Zero: The Biography of a Dangerous Idea. Penguin. pp. 167–169. ISBN 0140296476.
- Sidharth, BG (2008). The Thermodynamic Universe. World Scientific. p. 134. ISBN 9812812342.
- ^ Adelberger, E; Dvali, G; Gruzinov, A (2007). "Photon Mass Bound Destroyed by Vortices". Physical Review Letters. 98: 010402. doi:10.1103/PhysRevLett.98.010402. arXiv:hep-ph/0306245.
- Pradhan, T (2001). The Photon. Nova Press. p. 44. ISBN 1560729287.
- Weyl, H. (1917). "Zur Gravitationstheorie". Annalen der Physik. 359 (18): 117–145. doi:10.1002/andp.19173591804.
Weyl, H. (1919). "Eine neue Erweiterung der Relativitätstheorie". Annalen der Physik. 364 (10): 101–133. doi:10.1002/andp.19193641002. -
AS (1931). "On the instability of Einstein's spherical world". Monthly Notices of the Royal Astronomical Society. 90: 669–678. Bibcode:1930MNRAS..90..668E.
{{cite journal}}: More than one of|author=and|last=specified (help) - Dirac, PAM (1937). "The Cosmological Constants". Nature. 139: 323. doi:10.1038/139323a0.
-
Ellis, GFR; Uzan, J-P (2005). "'c' is the speed of light, isn't it?". American Journal of Physics: 240–247. arXiv:gr-qc/0305099.
The possibility that the fundamental constants may vary during the evolution of the universe offers an exceptional window onto higher dimensional theories and is probably linked with the nature of the dark energy that makes the universe accelerate today.
- An overview can be found in the dissertation of
Mota, DF (2006). "Variations of the fine structure constant in space and tim". arXiv:astro-ph/0401631`.
{{cite arXiv}}:|class=ignored (help); Check|arxiv=value (help) - Uzan, J-P (2003). "The fundamental constants and their variation: observational status and theoretical motivations". Reviews of Modern Physics. 74: 403. arXiv:hep-ph/0205340.
- Kafatos, M; Roy, S; Roy, M (2005). "Variation of Physical Constants, Redshift and the Arrow of Time". Acta Physica Polonica B. 36: 3139–3162. arXiv:astro-ph/0305117.
-
Farrell, DJ; Dunning-Davies, J (2007). "The constancy, or otherwise, of the speed of light". In Ross, LV (ed.). New Research on Astrophysics, Neutron Stars and Galaxy Clusters. Nova Publishers. pp. 71ff. ISBN 1600211100.
{{cite book}}: External link in|chapterurl=|chapterurl=ignored (|chapter-url=suggested) (help) -
Amelino-Camelia, G (2008). "Quantum Gravity Phenomenology". arXiv:0806.0339 .
{{cite arXiv}}: More than one of|author1=and|last=specified (help) - Gambini, R; Pullin, J (1999). "Nonstandard optics from quantum spacetime". Physical Review D. 59: 124021. doi:10.1103/PhysRevD.59.124021. arXiv:gr-qc/9809038.
- Smolin, L (2000). Three roads to quantum gravity. Basic Books. p. 216. ISBN 0465078362.
- Wanjek, C. "Quantum Gravity – Revealed by Gamma Ray Bursts?". Astronomy Today. Retrieved 2009-08-21.
-
Schaefer, BE (1999). "Severe limits on variations of the speed of light with frequency". Physical Review Letters. 82: 4964–4966. doi:10.1103/PhysRevLett.82.4964. arXiv:astro-ph/9810479.
{{cite journal}}: More than one of|author=and|last=specified (help) - Ellis, J; Mavromatos, DV; Sakharov, AS (2003). "Quantum-Gravity Analysis of Gamma-Ray Bursts using Wavelets". Astronomy & Astrophysics. 403: 409–424. doi:10.1051/0004-6361:20030263. arXiv:astro-ph/0210124.
- Füllekrug, M (2004). "Probing the Speed of Light with Radio Waves at Extremely Low Frequencies". Physical Review Letters. 93: 043901. doi:10.1103/PhysRevLett.93.043901.
- Feynman, RP (1963). Lectures on Physics Volume II. Addison-Wesley. pp. 32:1–32:3.
- Henderson, T. "Lesson 2: The Mathematics of Refraction". The Physics Classroom Tutorial. Retrieved 2009-08-21.
- Hau, LV; Harris, SE; Dutton, Z; Behroozi, CH (1999). "Light speed reduction to 17 metres per second in an ultracold atomic gas" (PDF). Nature. 397: 594–598. doi:10.1038/17561.
- Liu, C; Dutton, Z; Behroozi, CH; Hau, LV (2001). "Observation of coherent optical information storage in an atomic medium using halted light pulses" (PDF). Nature. 409: 490–493. doi:10.1038/35054017.
- Bajcsy, M; Zibrov, AS; Lukin, MD (2003). "Stationary pulses of light in an atomic medium". Nature. 426: 638–641. doi:10.1038/nature02176.
- Dumé, B (2003). "Switching light on and off". Physics World. Retrieved 2008-12-08.
- Taylor, EF; Wheeler, JA (1992). Spacetime Physics. W. H. Freeman. pp. 74–75. ISBN 0716723271.
- Egan, G. (2000). "Subluminal". Retrieved 2007-02-06.
- Wang, LJ; Kuzmich, A; Dogario, A (2000). "Gain-assisted superluminal light propagation". Nature. 406 (406): 277. doi:10.1038/35018520.
- Whitehouse, D (2000). "Beam smashes light barrier". BBC News. Retrieved 2008-12-08.
- Brunner, N; Scarani, V; Wegmüller, M; Legré, M; Gisin, N (2004). "Direct Measurement of Superluminal Group Velocity and Signal Velocity in an Optical Fiber". Physical Review Letters. 93 (20): 203902. doi:10.1103/PhysRevLett.93.203902.
- Gibbs, P (1997). "Is Faster-Than-Light Travel or Communication Possible?". University of California, Riverside. Retrieved 2008-08-20.
- Wertheim, M (2007). "The Shadow Goes". New York Times. Retrieved 2009-08-21.
-
Muga, JG; Mayato, RS; Egusquiza, IL, eds (2007). Time in Quantum Mechanics. Springer. p. 48. ISBN 3540734724.
{{cite book}}:|author=has generic name (help)CS1 maint: multiple names: authors list (link) - Hernández-Figueroa, HE; Zamboni-Rached, M; Recami, E (2007). Localized Waves. Wiley Interscience. p. 26. ISBN 0470108851.
- Wynne, K (2002). "Causality and the nature of information" (PDF). Optics Communications. 209: 84–100.
- Rees, M (1966). "The Appearance of Relativistically Expanding Radio Sources". Nature. 211: 468. doi:10.1038/211468a0.
- Čerenkov, PA (1934). "Visible Emission of Clean Liquids by Action of γ Radiation". Dokl. Akad. Nauk SSSR. 2: 451. Reprinted in "Selected Papers of Soviet Physicists". Usp. Fiz. Nauk. 93: 385. 1967.
- Čerenkov, EP (1999). Gorbunova, AN (ed.). Pavel Alekseyevich Čerenkov: Chelovek i Otkrytie. Nauka. pp. 149–153.
- AG Kirk (2006). "Free-space optical interconnects". In Lorenzo Pavesi, Gérard Guillot (ed.). Optical Interconnects: The silicon approach. Birkhäuser. p. 343. ISBN 3540289100.
-
Hall, S.H. and Hall, G.W. and McCall, J.A. (2000). High Speed Digital System Design: A Handbook of Interconnect Theory and Design Practices. Wiley New York.
{{cite book}}: CS1 maint: multiple names: authors list (link) -
E Gad, M Nakla & R Achar (2008). "Model-order reduction of high-speed interconnects using integrated congruence transform". Model Order Reduction. Springer. p. 362. ISBN 3540788409.
{{cite book}}: Unknown parameter|editors=ignored (|editor=suggested) (help) - Further discussion can be found at NASA StarChild
- ^ R.J. MacKay, R.W. Oldford (2000). "Scientific Method, Statistical Method and the Speed of Light". Statistical Science. 15 (3): 254–278. doi:10.1214/ss/1009212817.
- B. Steffens (2006). "Chapter Five – The Scholar of Cairo". Ibn al-Haytham: First Scientist. Morgan Reynolds. ISBN 1599350246.
- S. Hamarneh (1972). "Review: Hakim Mohammed Said, Ibn al-Haitham". Isis. 63 (1): 119. doi:10.1086/350861.
- ^ P.M. Lester (2005). Visual Communication: Images With Messages. Thomson Wadsworth. pp. 10–11. ISBN 0534637205.
- O'Connor, John J.; Robertson, Edmund F., "Abu Ali al-Hasan ibn al-Haytham", MacTutor History of Mathematics Archive, University of St Andrews
- P. Lauginie (2005). "Measuring: Why? How? What?" (PDF). Eighth International History, Philosophy, Sociology & Science Teaching Conference. Retrieved 2008-07-18.
- O'Connor, John J.; Robertson, Edmund F., "Abu Arrayhan Muhammad ibn Ahmad al-Biruni", MacTutor History of Mathematics Archive, University of St Andrews
- David C. Lindberg (1996). Roger Bacon and the origins of Perspectiva in the Middle Ages: a critical edition and English translation of Bacon's Perspectiva, with introduction and notes. Oxford University Press. p. 143. ISBN 0198239920.
- David C. Lindberg (1974). "Late Thirteenth-Century Synthesis in Optics". In Edward Grant (ed.). A source book in medieval science. Harvard University Press. p. 396. ISBN 9780674823600.
- P. Marshall (1981). "Nicole Oresme on the Nature, Reflection, and Speed of Light". Isis. 72 (3): 357–374 . doi:10.1086/352787.
-
Sayana-commentary on Rigveda 1.50, see:
M. Müller (ed.) (1890). Rig-Veda-Samhita, together with the Commentary of Sayana. London: Oxford University Press.
{{cite book}}:|author=has generic name (help) - H.G. Topdemir (1999). Takîyüddîn'in Optik Kitabi. Ankara: Ministry of Culture Press. (cf. H.G. Topdemir (2008). Taqi al-Din ibn Ma‘ruf and the Science of Optics: The Nature of Light and the Mechanism of Vision. FSTC. Retrieved 2007-07-04.)
- Boyer, Carl B. (1941). "Early Estimates of the Velocity of Light". Isis. 33 (1): 24. doi:10.1086/358523.
-
Galilei, Galileo (1954) . Dialogues Concerning Two New Sciences. translated by Henry Crew and Alfonso de Salvio. New York, NY: Dover Publications Inc. ISBN 486-60099-8.
{{cite book}}: Check|isbn=value: length (help); External link in|title= - ^
Teuber, Jan (2004). "Ole Rømer og den bevægede Jord – en dansk førsteplads?". In Friedrichsen, Per; Henningsen, Ole; Olsen, Olaf; Thykier, Claus; Tortzen, Chr. Gorm (ed.). Ole Rømer – videnskabsmand og samfundstjener. Kroppedal, Studier i astronomi, Nyere tid, Arkæologi. Gads. pp. 217–219. ISBN 87-12-04139-4.
{{cite book}}: CS1 maint: multiple names: editors list (link) Template:Da icon - The history of these events has often been incorrectly reported, and the reader might wonder if it is correctly reported here. An account of this historical mix-up is found in AP French (1990). "Roemer: a cautionary tale". In John Roche (ed.). Physicists look back: studies in the history of physics. CRC Press. pp. 120–121. ISBN 0852740018.
-
Olivier Darrigol (2000). Electromagnetism from Ampère to Einstein. p. 147.
{{cite book}}: Unknown parameter|ulr=ignored (help) -
Maxwell "part I of A Dynamical Theory of the Electromagnetic Field". 1865.
{{cite web}}: Check|url=value (help) -
Maxwell "p. 499 in A Dynamical Theory of the Electromagnetic Field". 1865.
{{cite web}}: Check|url=value (help) -
Maxwell "pages 480-486 in A Dynamical Theory of the Electromagnetic Field". 1865.
{{cite web}}: Check|url=value (help) -
Michelson, Albert Abraham & Morley, Edward Williams (1887). "On the Relative Motion of the Earth and the Luminiferous Ether" . American Journal of Science. 34: 333–345.
{{cite journal}}: CS1 maint: multiple names: authors list (link) -
Kittel, Knight, Ruderman, Helmholtz, Moyer (1973). Berkley Physics Course. Vol. 1. McGraw Hill. pp. 312–317. ISBN 0-07-004880-0.
{{cite book}}: CS1 maint: multiple names: authors list (link) - R C Cialdea, Lett Nuovo Cimento 4 (1972) 821
- D C Champeny, G R Isaak, and A M Kahn, Phys Lett 7 (1963) 241
- A detailed discussion of the interferometer and its use for determining the speed of light can be found in J. M. Vaughan (1989). The Fabry-Perot interferometer. CRC Press. pp. 47 and 384–391. ISBN 0852741383.
-
J. Cooke, M. Martin, H. McCartney, B. Wilf (1968). "Direct determination of the speed of light as a general physics laboratory experiment". American Journal of Physics. 36 (9): 847. doi:10.1119/1.1975166.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - K. Aoki, T. Mitsui (2008). "A small tabletop experiment for a direct measurement of the speed of light". American Journal of Physics. 76 (9): 812–815. doi:10.1119/1.2919743.
-
M.B. James, R.B. Ormond, A.J. Stasch (1999). "Speed of light measurement for the myriad". American Journal of Physics. 67 (8): 681–684. doi:10.1119/1.19352.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Resolution 1
- BG Zagar (1999). "Laser Interferometer Displacement Sensors; §6.5". In JG Webster (ed.). The Measurement, Instrumentation, and Sensors Handbook. CRC Press. p. 6-69. ISBN 0849383471.
-
J Flügge; et al. (2004). "Fundamental length metrology: Practical issues; §D.2.1.3". In CE Webb & JDC Jones (ed.). Handbook of Laser Technology and Applications. Taylor & Francis. pp. 1737 ff. ISBN 0750309660.
{{cite book}}: Explicit use of et al. in:|author=(help) - "Definition of the meter".
- "NIST document" (PDF). p. 191.
- David A Cardwell, David S Ginley (2003). Characterization, Applications and Cryogenics. CRC Press. p. 1251. ISBN 0750308974.
- Lee Smolin (2007). The Trouble with Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next. Houghton Mifflin Harcourt. p. 215. ISBN 061891868X.
-
Peter Woit (2006). Not even wrong: the failure of string theory and the search for unity in physical law. Basic Books. p. 6. ISBN 0465092756.
Setting the speed of light equal to one determines the choice of units used to measure time in terms of the units to measure space, and vice versa.
- The table is p. 249; CI-2006, Recommendation 1 of CIPM of 2006.
- A list of the resulting wavelengths based upon these frequencies and λ = c/f is found at BIPM mise-en-pratique, method b.
Historical references
- Rømer, Ole (1676). "Démonstration touchant le mouvement de la lumière". Journal des sçavans: 223–236. Template:Fr icon. Translated as "A Demonstration concerning the Motion of Light" (). Philosophical Transactions of the Royal Society (136): 893–894. 1677.
- Halley, Edmund (1694). "Monsieur Cassini, his New and Exact Tables for the Eclipses of the First Satellite of Jupiter, reduced to the Julian Stile and Meridian of London". Philosophical Transactions of the Royal Society. 18 (214): 237–256.
- Fizeau, H. L. (1849). Sur une expérience relative à la vitesse de propagation de la lumière. Comptes rendus de l'Académie des sciences (Paris). Vol. 29. pp. 90–92, 132. Template:Fr icon
- Foucault, J. L. (1862). Détermination expérimentale de la vitesse de la lumière: parallaxe du Soleil. Comptes rendus de l'Académie des sciences (Paris). Vol. 55. pp. 501–503, 792–796.
- Michelson, A. A. (1878). Experimental Determination of the Velocity of Light. Proceedings of the American Association of Advanced Science. Vol. 27. pp. 71–77.
- Newcomb, Simon (1886). "The Velocity of Light". Nature: 29–32.
- Perrotin, Joseph (1900). "Sur la vitesse de la lumière". C. R. Acad. Sci. Paris. 131: 731–734. Template:Fr icon
- Michelson, A. A.; Pease, F. G.; Pearson, F. (1935). "Measurement Of The Velocity Of Light In A Partial Vacuum". Astrophys. J. 82: 26–61. doi:10.1086/143655.
Modern references
- Brillouin, Léon (1960). Wave propagation and group velocity. Academic Press.
- Jackson, John David (1975). Classical electrodynamics (2nd ed.). John Wiley & Sons. ISBN 0-471-30932-X.
- MacKay, R. J.; Oldford, R. W. (2000). "Scientific Method, Statistical Method and the Speed of Light". Statistical Science. 15 (3): 254–278. doi:10.1214/ss/1009212817.
- Keiser, Gerd (2000). Optical Fiber Communications (3rd ed.). McGraw-Hill. p. 32. ISBN 0072321016.
- Y Jack Ng (2004). "Quantum Foam and Quantum Gravity Phenomenology". In Giovanni Amelino-Camelia & Jerzy Kowalski-Glikman (editors) (ed.). Planck Scale Effects in Astrophysics and Cosmology. Springer. pp. 321ff. ISBN 3540252630.
{{cite book}}:|editor=has generic name (help) - J Helmcke & F Riehle (2001). "Physics behind the definition of the meter". In T. J. Quinn, S. Leschiutta, P. Tavella (ed.). Recent advances in metrology and fundamental constants. IOS Press. p. 453. ISBN 1586031678.
{{cite book}}: CS1 maint: multiple names: editors list (link) - M. J. Duff (2004). "Comment on time-variation of fundamental constants". ArXiv preprint.
External links
- Speed of light in vacuum (at NIST)
- Definition of the metre (BIPM)
- Data Gallery: Michelson Speed of Light (Univariate Location Estimation) (download data gathered by A.A. Michelson)
- Subluminal (Java applet demonstrating group velocity information limits)
- De Mora Luminis at MathPages
- Light discussion on adding velocities
- Speed of Light (University of Colorado Department of Physics)
- How is the speed of light measured?
- The Fizeau "Rapidly Rotating Toothed Wheel" Method
| Extremes of motion | |
|---|---|
| Speed | |
| Distance | |
| Endurance | |
| See also | |
Template:Link FA Template:Link FA Template:Link FA
Categories:
