| Revision as of 22:19, 2 December 2005 edit69.47.4.24 (talk) →An example← Previous edit | Revision as of 06:37, 15 December 2005 edit undoSahodaran (talk | contribs)754 editsm →Control specificationsNext edit → | ||
| Line 90: | Line 90: | ||
| Several different control strategies have been devised in the past years. These vary from extremally general ones (]), to others devoted to very particulars classes of systems (es. ] or ] cruise control). | Several different control strategies have been devised in the past years. These vary from extremally general ones (]), to others devoted to very particulars classes of systems (es. ] or ] cruise control). | ||
| A control problem can have several specifications. Stability, of course, is always present: the controller must |
A control problem can have several specifications. Stability, of course, is always present: the controller must ensure that the closed-loop system is stable: this both if the open-loop is stable or not. An unaccurate choose of the controller, indeed, can even worsen the stability properties of the open-loop system. This must normally be avoided. Sometimes it would be desired to obtain a particular dynamics in the closed loop: i.e. that the poles have <math>Re < -\overline{\lambda}</math>, where <math>\overline{\lambda}</math> is a fixed value stricly greater than zero, instead of simply ask that <math>Re<0</math>. | ||
| Another typical specification is the rejection of a step disturbance: this can be easily obtained by including an ] in the open-loop chain (i.e. directly before the system under control). Other classes of disturbances need different types of sub-systems to be included. | Another typical specification is the rejection of a step disturbance: this can be easily obtained by including an ] in the open-loop chain (i.e. directly before the system under control). Other classes of disturbances need different types of sub-systems to be included. | ||
Revision as of 06:37, 15 December 2005
- For the sociological theory of deviant behavior, see Control theory (sociology).
In engineering and mathematics, control theory deals with the behavior of dynamical systems over time. The desired output of a system is called the reference variable. When one or more output variables of a system need to show a certain behaviour over time, a controller manipulates the inputs to a system to obtain the desired effect on the output of the system.
An example
As an example, consider cruise control. In this case, the system is a car. The goal of cruise control is to keep the car at a constant speed. Here, the output variable of the system is the speed of the car. The primary means to control the speed of the car is the air-fuel mixture being fed into the engine.
A simple way to implement cruise control is to lock the position of the throttle the moment the driver engages cruise control. This is fine if the car is driving on perfectly flat terrain. On hilly terrain, the car will slow down when going uphill and accelerate when going downhill; something its driver may find highly undesirable.
This type of controller is called an open-loop controller because there is no direct connection between the output of the system and its input. One of the main disadvantages of this type of controller is the lack of sensitivity to the dynamics of the system under control.
The actual way that cruise control is implemented involves feedback control, whereby the speed is monitored and the amount of throttle is increased if the car is driving slower than the intended speed and decreased if the car is driving faster. This feedback makes the car less sensitive to disturbances to the system, such as changes in slope of the ground or wind speed. This type of controller is called a closed-loop controller.
History
Although control systems of various types date back to antiquity, a more formal analysis of the field began with a dynamics analysis of the centrifugal governor, conducted by the famous physicist J.C. Maxwell in 1868 entitled "On Governors." This described and analyzed the phenomenon of "hunting" in which lags in the system can lead to overcompensation and unstable behavior. This caused a flurry of interest in the topic, which was followed up by Maxwell's classmate, E.J. Routh, who generalized the results of Maxwell for the general class of linear systems. This result is called the Routh-Hurwitz Criterion.
A notable application of dynamic control was in the area of manned flight. The Wright Brothers made their first successful test flights in December 17, 1903 and by 1904 Flyer III and were distinguished by their ability to control their flights for substantial periods (more so than the ability to produce lift from an airfoil, which was known). Control of the airplane was necessary for its safe, economical, and economically successful use.
By World War II, control theory was an important part of fire control, guidance, and cybernetics. The Space Race to the Moon depended on accurate control of the spacecraft. But control theory is not only useful in technological applications, and is meeting an increasing use in field such economics and sociology.
Classical control theory
To avoid the problems of the open-loop controller, control theory introduces feedback. The output of the system is fed back to the reference value , through the measurement performed by a sensor. The controller C then takes the difference between the reference and the output, the error e, to change the inputs u to the system under control P. This is shown in the figure. This kind of controller is a closed-loop controller or feedback controller.
This is a so-called single-input-single-output (SISO) control system: example where one or more variables can contain more than a value (MIMO, i.e. Multi-Input-Multi-Output - for example when outputs to be controlled are two or more) are frequent. In such cases variables are represented through vectors instead of simple scalar values.
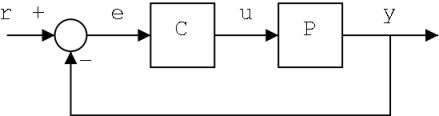
A simple feedback control loop
If we assume the controller C and the plant P are linear and time-invariant (i.e.: elements of their transfer function and do not depend on time), we can analyze the system above by using the Laplace transform on the variables. This gives us the following relations:
Solving for Y(s) in terms of R(s), we obtain:
The term is referred to as the transfer function of the system. If we can ensure , i.e. it has very great norm with each value of , then is approximately equal to . This means we control the output by simply setting the reference.
Stability
Stability (in control theory) means that for any bounded input over any amount of time, the output will also be bounded. This is known as BIBO stability (see also Lyapunov stability). If a system is BIBO stable then the output cannot "blow up" if the input remains finite. Mathematically, this means that for a linear continuous-time system to be stable all of the poles of its transfer function must
- lie in the left half of the complex plane if the Laplace transform is used (i.e. its real part is less than zero)
OR
- lie inside the unit circle if the Z-transform is used (i.e. its module is less than one)
In the two cases, if respectively the pole has a real part strictly smaller of zero or a module strictly smaller than one, we speak of asymptotic stability: the variables of an asymptotically stable control system always decrease from their initial value and do not show permanent oscillations, which are instead present if a pole has exactly a real part equal to zero (or a module equal to one). If a simply stable system response neither decays nor grows over time, and has no oscillations, it referred to as marginally stable: in this case it has non-repeated poles along the vertical axis (i.e. their real and complex component is zero). Oscillations are present when poles with real part equal to zero have also complex part not equal to zero.
Difference between the two cases are not a contradiction. The Laplace transform is in Cartesian coordinates and the Z-transform is in circular coordinates and it can be shown that
- the negative-real part in the Laplace domain can map onto the interior of the unit circle
- the positive-real part in the Laplace domain can map onto the exterior of the unit circle
If the system in question has an impulse response of
and considering the Z-transform (see this example), it yields
which has a pole in (zero imaginary part). This system is BIBO (asymptotically) stable since the pole is inside the unit circle.
However, if the impulse response was
then the Z-transform is
which has a pole at and is not BIBO stable since the pole has a module strictly greater than one.
Nemerous tools exist for the analysis of the poles of a system. These include graphicals system like the Root locus or the Nyquist plots.
Controllability and observability
Controllability and observability are main issues in the analysis of system before decide the best control strategy to be applied. Controllability is related to the possibility to force the system in a particular state by using an appropriate control signal. If a state is not controllable, then no signal will ever be able to force the system to reach a level of controllability. Observability instead is related to the possibility to "observe", through output measurements, the system occupying a state. If a state is not observable, the controller will never be able to correct the closed-loop behaviour if such a state is not desirable.
From a geometrical point of view, if we look at the states of each variable of the system to be controlled, every "bad" state of these variables must be controllable and observable to ensure a good behaviour in the closed-loop system. That is, if one of the eigenvalues of the system is not both controllable and observable, this part of the dynamics will remain untouched in the closed-loop system. If such an eigenvalue is not stable, the dynamics of this eigenvalue will be present in the close-loop system which therefore will be unstable. Unobservable poles are not present in the transfer function realization of a state-space representation, which is why sometimes the latter is preferred in dynamical systems analysis.
Solutions to problems of uncontrollable or unobservable system include adding actuators and sensors.
Control specifications
Several different control strategies have been devised in the past years. These vary from extremally general ones (PID controllers), to others devoted to very particulars classes of systems (es. Robotics or Aircraft cruise control).
A control problem can have several specifications. Stability, of course, is always present: the controller must ensure that the closed-loop system is stable: this both if the open-loop is stable or not. An unaccurate choose of the controller, indeed, can even worsen the stability properties of the open-loop system. This must normally be avoided. Sometimes it would be desired to obtain a particular dynamics in the closed loop: i.e. that the poles have , where is a fixed value stricly greater than zero, instead of simply ask that .
Another typical specification is the rejection of a step disturbance: this can be easily obtained by including an integrator in the open-loop chain (i.e. directly before the system under control). Other classes of disturbances need different types of sub-systems to be included.
Other "classical" control theory specifications regard the time-response of the closed-loop system: these include the lead-time (the time needed by the control system to reach the desired value after a perturbation), over-elongation (the highest value reached by the response before reaching the desired value) and others. Frequency domain specifications are usually related to robustness (see after).
Model identification and robustness
Main article: Model identificationA control system must always have some robustness property. A robust controller is such that his properties do not change much if applied to a system slightly different from the mathematical one used for its synthesis. This specification is important: no real physical system truly behaves like the series of differential equations used to represent it in mathematical way. Sometimes a simpler mathematical model can be chosen in order to simplfy calculations. Otherwise the true system dynamics can result so complicated that a complete modelization is impossible.
System identification
The process of determination of the equations of a model's dynamics is called model identification. This can be done off-line: for example, executing a series of measure from which calculate an approximated mathematical model, typically its transfer function or matrix. Such identification from the output, however, cannot take account of unobservable dynamics. Sometimes the model is built directly starting from known physical equations: for example, in the case of a spring-dump system we know that . Even if assuming that a "complete" model is used, all the parameters included in these equations (called "nominal parameters") are never known with absolute precision: therefore the control system will have to behave correctly even in presence of their true values.
Some advanced control techniques include an "on-line" identification process (see later). The parameters of the model are calculated ("identified") while the controller itself is running: in this way, if a drastical variation of the parameters ensues (for example, if the robot's arm releases a weight), the controller will adjust himself consequently in order to ensure the correct performance.
Analysis
Analysis of the robustness of a SISO control system can be performed in the frequency domain, considering the system's transfer function and using Nyquist and Bode diagrams. Topics include Phase margin and Amplitude margin. For MIMO and, in general, more complicated control systems one must consider the theorical results devised for each control technique (see next section): i.e., if particular robustness qualities are needed, the engineer must shift his attention to a technique including it in its properties.
Constraints
A particular robustness issue is the possibility of a control system to work even in presence of constraints. In the practice every signal is physically limited. It could happen that in its true working a controller will try to send signals that cannot be performed by the machinery: for example, trying to rotate a valve at excessive speed. This can provoke a bad behaviour of the closed-loop system, or even break up actuators or other subsystems. Specifical control techniques are known that can solve the problem: model predictive control (see later), and anti-wind up systems. The latter consist in another control block that is added to a previously synthesized controller, and ensures that the control signal never overcomes the threshold given.
Main control strategies
Every control system must guarantee first the stability of the closed-loop behaviour. For linear systems, this can be obtained directly placing the poles. Non-linear control systems used instead specifical theories (normally based on Lyapunov Theory) to ensure stability without regard to inner dynamics of the systems. The possibility to fulfil different specifications varies from the model considered and/or the control strategy chosen. Here a summary list of the main control techniques is shown:
PID controllers
Main article: PID controllerUsing a so called PID controller is probably the most used control techinques, being the simplest one. "PID" means: Proportional-Integral-Derivative, referring to the three types of sub.-system which can be added before the system under control. If is the control signal sent to the system and its measured output, a PID controller has the generical form
The desired closed loop dynamics can be easily obtained by adjusting the three parameters , and . Stability can be ensured using only the proportional term, but the integral term permits the rejection of a step disturbance (often a striking specification in process control). The derivative term is often omitted. PID controllers are the easiest class of control systems: however, they cannot be used in several more complicated cases, especially if MIMO systems are considered.
Direct pole placement
Main article: State space (controls)For MIMO systems, pole placement can be performed mathematically using a State space representation of the open-loop system and calculating a feedback matrix assigning poles in the desired positions. In complicated system this can need large computer-assisted calculation capabilities, and not always can ensure robust results.
Optimal control
Main article: Optimal controlOptimal control is a particular control technique in which the control signal optimizes a certain "Cost index": for example, in the case of a satellite we could need to know the jets to give in order to bring it again in the desired trajectory after a perturbation, consuming as less as possible fuel in the process. Two classes of optimal controls have been widely used in industrial applications, as it has been showed they can ensure closed-loop stability also. These are Model predictive control (MPC) and Linear-Quadratic-Gaussian control (LQG). The first is the most successful one, as it can take account of the presence of constrains over the signals present in the systems, which is an important topic in many industrial processes (by the way, the "optimal control" structure in MPC is only a mean to achieve such a result, as it does not optimize a true perormance index as a closed-loop control system). Together with PID controllers, MPC systems are the most widely used control technique in process control.
See also:
Adaptive control
Main article: Adaptive controlAdaptive control uses an on-line identification of the process parameters, obaining strong robustness properties. Adaptive controls were applied for the first time in the {{Aircraft industry]] in the 1950s, and have found a particular ground of success in that field.
Non-linear control systems
Main article: Non-linear controlProcesses of industries like Robotics and Aerospace industry have typically a strong non-linear dynamics. In control theory is sometimes possible to linearize such class of system and apply linear techniques: but in many cases it had been necessary to devise from the scratch theories permitting control of non-linear system. These normally take advantage of results based on Lyapunov's theory.
See also
- Control engineering
- Intelligent control
- Model identification
- Process control
- Robotic unicycle
- Root locus
- Servomechanism
- State space (controls)
- Fractional order control
- Stable polynomial
- Robust control
Appendix A
Derivation of transfer function:
| (1) | ||
| (2) | ||
| (3) | ||
| (1) + (2) | (4) | |
| (4) + (3) | ||
| Expanding out ( R − Y ) | ||
| Moving P C Y to the left hand side | ||
| Consolidating the common term Y | ||
| Isolating out the term Y | ||
| (5) |
 is fed back to the reference value
is fed back to the reference value  , through the measurement performed by a sensor. The controller C then takes the difference between the reference and the output, the error e, to change the inputs u to the system under control P. This is shown in the figure. This kind of controller is a
, through the measurement performed by a sensor. The controller C then takes the difference between the reference and the output, the error e, to change the inputs u to the system under control P. This is shown in the figure. This kind of controller is a  and
and  do not depend on time), we can analyze the system above by using the
do not depend on time), we can analyze the system above by using the 



 is referred to as the
is referred to as the  , i.e. it has very great
, i.e. it has very great  , then
, then  is approximately equal to
is approximately equal to  . This means we control the output by simply setting the reference.
. This means we control the output by simply setting the reference.


 (zero
(zero 

 and is not BIBO stable since the pole has a module strictly greater than one.
and is not BIBO stable since the pole has a module strictly greater than one.
 , where
, where  is a fixed value stricly greater than zero, instead of simply ask that
is a fixed value stricly greater than zero, instead of simply ask that  .
.
 . Even if assuming that a "complete" model is used, all the parameters included in these equations (called "nominal parameters") are never known with absolute precision: therefore the control system will have to behave correctly even in presence of their true values.
. Even if assuming that a "complete" model is used, all the parameters included in these equations (called "nominal parameters") are never known with absolute precision: therefore the control system will have to behave correctly even in presence of their true values.
 is the control signal sent to the system and
is the control signal sent to the system and 
 ,
,  and
and  . Stability can be ensured using only the proportional term, but the integral term permits the rejection of a step disturbance (often a striking specification in
. Stability can be ensured using only the proportional term, but the integral term permits the rejection of a step disturbance (often a striking specification in 





